Chuyên đề Đường thẳng và Đường cong là một phần quan trọng trong chương trình Hình học, đặc biệt ở các lớp 10, 11 và 12. Việc nắm vững kiến thức về đường thẳng và đường cong là nền tảng để giải quyết nhiều bài toán thực tế và nâng cao khả năng tư duy logic.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng chi tiết, bài tập đa dạng và phương pháp giải bài tập hiệu quả, giúp bạn dễ dàng tiếp cận và chinh phục chuyên đề này.
Giải Đường thẳng - Đường cong trang 50, 51 SGK Toán 2 Chân trời sáng tạo. Bài 1. Bạn kiến nào bò theo đường thẳng?
Bài 1 (trang 50 SGK Toán 2 tập 1)
Bạn kiến nào bò theo đường thẳng?
Bạn kiến nào bò theo đường cong.

Phương pháp giải:
- Xem lại về hình dạng của đường thẳng, đường cong.
- Quan sát hình vẽ để xác định mỗi bạn kiến đi theo đường thẳng hay đường cong.
Lời giải chi tiết:
- Bạn kiến đỏ bò theo đường cong.
- Bạn kiến xanh lá cây bò theo đường thẳng.
- Bạn kiến xanh da trời bò theo đường cong.
Đọc tên các đoạn thẳng, đường thẳng.
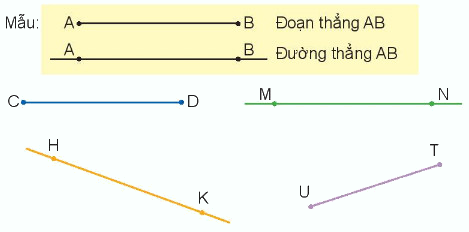
Phương pháp giải:
- Quan sát hình vẽ để nhận biết đoạn thẳng, đường thẳng:
+ Đoạn thẳng là đoạn nối liền hai điểm lại với nhau.
+ Kéo dài đoạn thẳng về hai phía ta được đường thẳng.
- Đọc tên các đoạn thẳng, đường thẳng theo mẫu đã cho.
Lời giải chi tiết:
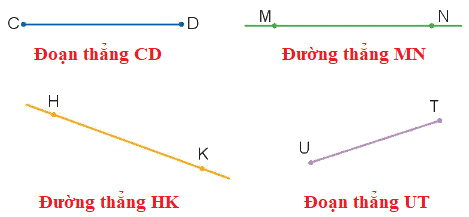
Bài 1 (trang 50 SGK Toán 2 tập 1)
Bạn kiến nào bò theo đường thẳng?
Bạn kiến nào bò theo đường cong.

Phương pháp giải:
- Xem lại về hình dạng của đường thẳng, đường cong.
- Quan sát hình vẽ để xác định mỗi bạn kiến đi theo đường thẳng hay đường cong.
Lời giải chi tiết:
- Bạn kiến đỏ bò theo đường cong.
- Bạn kiến xanh lá cây bò theo đường thẳng.
- Bạn kiến xanh da trời bò theo đường cong.
Đọc tên các đoạn thẳng, đường thẳng.
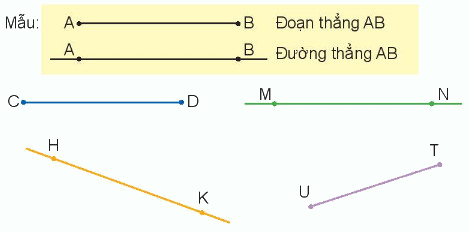
Phương pháp giải:
- Quan sát hình vẽ để nhận biết đoạn thẳng, đường thẳng:
+ Đoạn thẳng là đoạn nối liền hai điểm lại với nhau.
+ Kéo dài đoạn thẳng về hai phía ta được đường thẳng.
- Đọc tên các đoạn thẳng, đường thẳng theo mẫu đã cho.
Lời giải chi tiết:
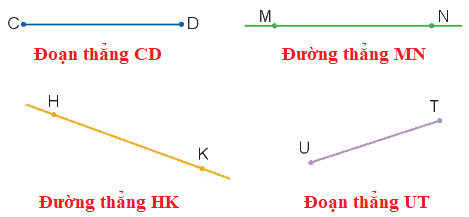
Đường thẳng là một khái niệm cơ bản trong hình học, được xác định bởi hai điểm phân biệt. Trong mặt phẳng tọa độ, đường thẳng có thể được biểu diễn bằng nhiều dạng phương trình khác nhau, mỗi dạng phù hợp với từng bài toán cụ thể.
Việc chuyển đổi giữa các dạng phương trình này là một kỹ năng quan trọng, giúp bạn linh hoạt trong việc giải quyết các bài toán liên quan đến đường thẳng.
Đường cong là một đường không thẳng, có thể là đường cong kín hoặc đường cong hở. Có rất nhiều loại đường cong khác nhau, mỗi loại có những đặc điểm và phương trình riêng.
Mỗi loại đường cong đều có những tính chất đặc trưng, như tiêu điểm, đường chuẩn, trục đối xứng,... Việc hiểu rõ những tính chất này giúp bạn phân tích và giải quyết các bài toán liên quan đến đường cong một cách hiệu quả.
Đường thẳng và đường cong có thể có nhiều mối quan hệ khác nhau, như cắt nhau, tiếp xúc nhau, hoặc không giao nhau. Việc xác định mối quan hệ này là một bài toán quan trọng trong hình học.
Để tìm giao điểm giữa đường thẳng và đường cong, ta cần giải hệ phương trình gồm phương trình của đường thẳng và phương trình của đường cong. Số nghiệm của hệ phương trình chính là số giao điểm của đường thẳng và đường cong.
Ví dụ, để tìm giao điểm giữa đường thẳng y = mx + b và đường tròn (x - a)2 + (y - b)2 = R2, ta thay y = mx + b vào phương trình đường tròn và giải phương trình bậc hai theo x. Số nghiệm của phương trình bậc hai này sẽ cho ta biết số giao điểm của đường thẳng và đường tròn.
Đường thẳng và đường cong có rất nhiều ứng dụng trong thực tế, từ việc thiết kế kiến trúc, xây dựng cầu đường, đến việc mô phỏng quỹ đạo của các vật thể trong không gian.
Việc hiểu rõ về đường thẳng và đường cong không chỉ giúp bạn giải quyết các bài toán trong sách giáo khoa, mà còn mở ra những ứng dụng thực tế vô cùng thú vị.
Để nắm vững kiến thức về đường thẳng và đường cong, bạn cần luyện tập giải nhiều bài tập khác nhau. Dưới đây là một số dạng bài tập thường gặp:
Hãy truy cập giaitoan.edu.vn để luyện tập với hàng ngàn bài tập đa dạng và được giải chi tiết bởi các giáo viên giàu kinh nghiệm.
Chuyên đề Đường thẳng và Đường cong là một phần quan trọng trong chương trình Hình học. Việc nắm vững kiến thức về đường thẳng và đường cong là nền tảng để giải quyết nhiều bài toán thực tế và nâng cao khả năng tư duy logic. Hy vọng rằng, với những kiến thức và bài tập được cung cấp tại giaitoan.edu.vn, bạn sẽ tự tin chinh phục chuyên đề này.