Bài học về thừa số và tích là một trong những khái niệm nền tảng quan trọng trong chương trình toán học, đặc biệt là ở giai đoạn đầu của bậc trung học cơ sở.
Hiểu rõ về thừa số và tích không chỉ giúp học sinh giải quyết các bài toán đơn giản mà còn là bước đệm quan trọng để tiếp thu các kiến thức toán học phức tạp hơn sau này.
Bài 1: Gọi tên các thành phần của phép nhân
Tìm tích, biết các thừa số lần lượt là:
Phương pháp giải:
Tính nhẩm kết quả phép nhân hai số để tìm tích.
Lời giải chi tiết:
Ta có 2 x 3 = 6 vậy tích là 6.
Ta có 4 x 5 = 20 vậy tích là 20.
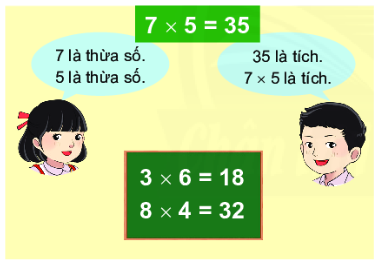
Thực hành "Lập tích"

Phương pháp giải:
Chọn 2 thẻ số có trong hình rồi lập tích của hai số đó.
Lời giải chi tiết:
Một số tích lập được là:
1 x 6 = 6
4 x 2 = 8
3 x 5 = 10
4 x 3 = 12
4 x 5 = 20
.....
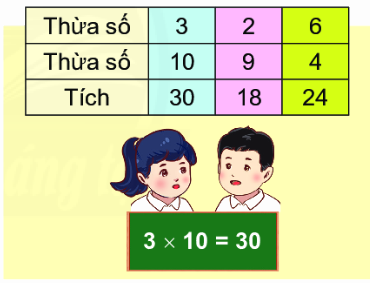
Nêu thừa số, tích trong các phép tính sau:
Phương pháp giải:
Dựa vào vị trí của các số trong phép nhân để xác định thừa số, tích.
Lời giải chi tiết:
- Trong phép nhân 5 x 2 = 10 có:
5 là thừa số
2 là thừa số
10 là tích
- Trong phép nhân 4 x 3 = 12 có:
4 là thừa số
3 là thừa số
12 là tích
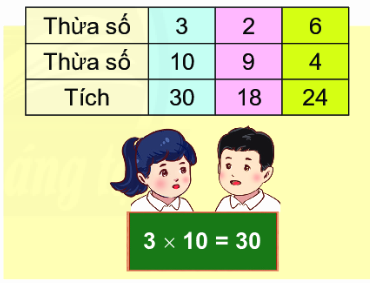
Nêu thừa số, tích trong các phép tính sau:
Phương pháp giải:
Dựa vào vị trí của các số trong phép nhân để xác định thừa số, tích.
Lời giải chi tiết:
- Trong phép nhân 5 x 2 = 10 có:
5 là thừa số
2 là thừa số
10 là tích
- Trong phép nhân 4 x 3 = 12 có:
4 là thừa số
3 là thừa số
12 là tích
Tìm tích, biết các thừa số lần lượt là:
Phương pháp giải:
Tính nhẩm kết quả phép nhân hai số để tìm tích.
Lời giải chi tiết:
Ta có 2 x 3 = 6 vậy tích là 6.
Ta có 4 x 5 = 20 vậy tích là 20.
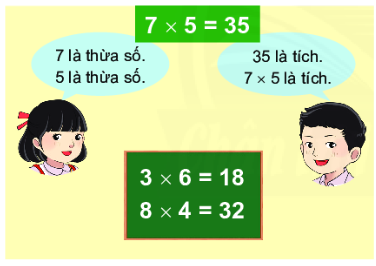
Thực hành "Lập tích"

Phương pháp giải:
Chọn 2 thẻ số có trong hình rồi lập tích của hai số đó.
Lời giải chi tiết:
Một số tích lập được là:
1 x 6 = 6
4 x 2 = 8
3 x 5 = 10
4 x 3 = 12
4 x 5 = 20
.....
Trong toán học, thừa số là những số được nhân với nhau để tạo ra một số khác. Ví dụ, trong phép nhân 2 x 3 = 6, số 2 và số 3 được gọi là thừa số, còn số 6 là tích.
Hiểu một cách đơn giản, thừa số là các thành phần tạo nên tích. Việc phân tích một số thành tích của các thừa số được gọi là phân tích thành thừa số. Đây là một kỹ năng quan trọng trong toán học, giúp chúng ta đơn giản hóa các bài toán và tìm ra các mối quan hệ giữa các số.
Một trường hợp đặc biệt của phân tích thành thừa số là phân tích một số ra thừa số nguyên tố. Số nguyên tố là số tự nhiên lớn hơn 1, chỉ chia hết cho 1 và chính nó. Ví dụ, 2, 3, 5, 7, 11,... là các số nguyên tố.
Để phân tích một số ra thừa số nguyên tố, ta thực hiện chia số đó cho các số nguyên tố nhỏ nhất (2, 3, 5, 7,...) cho đến khi kết quả là 1. Ví dụ, phân tích số 36 ra thừa số nguyên tố:
Vậy, 36 = 2 x 2 x 3 x 3 = 22 x 32.
Thừa số và tích có rất nhiều ứng dụng trong toán học, bao gồm:
Dưới đây là một số bài tập để bạn luyện tập về thừa số và tích:
Ngoài các khái niệm cơ bản về thừa số và tích, còn có một số khái niệm liên quan khác mà bạn có thể tìm hiểu thêm, như:
Thừa số và tích là những khái niệm cơ bản nhưng vô cùng quan trọng trong toán học. Việc nắm vững kiến thức về thừa số và tích sẽ giúp bạn giải quyết các bài toán một cách dễ dàng và hiệu quả hơn. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.