Đường gấp khúc là một khái niệm quan trọng trong hình học, thường xuất hiện trong chương trình toán lớp 6 và lớp 7. Hiểu rõ về đường gấp khúc giúp học sinh phát triển tư duy logic và khả năng giải quyết vấn đề.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng chi tiết, bài tập đa dạng và phương pháp giải bài tập đường gấp khúc một cách dễ hiểu, giúp bạn nắm vững kiến thức một cách nhanh chóng.
Giải Đường gấp khúc trang 52, 53 SGK Toán 2 Chân trời sáng tạo. Bài 1. Xếp đường gấp khúc
Bài 1 (trang 53 SGK Toán 2 tập 1)
Nói theo mẫu.
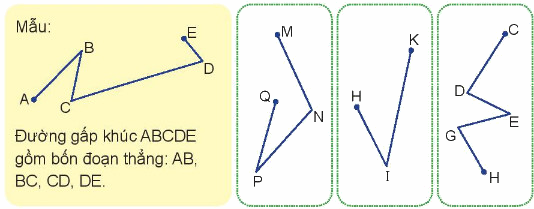
Phương pháp giải:
Quan sát hình vẽ để tìm các đoạn thẳng có trong mỗi đường gấp khúc và nói tương tự như mẫu đã cho.
Lời giải chi tiết:
- Đường gấp khúc MNPQ gồm ba đoạn thẳng: MN, NP, PQ.
- Đường gấp khúc HIK gồm hai đoạn thẳng: HI, IK.
- Đường gấp khúc CDEGH gồm bốn đoạn thẳng: CD, DE, EG, GH.
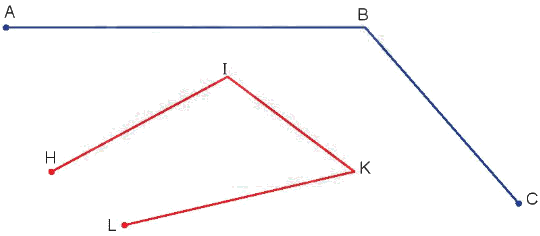
Đo rồi tính độ dài mỗi đường gấp khúc.
Đường gấp khúc ABC dài .?.cm.
Đường gấp khúc HIKL dài .?.cm.
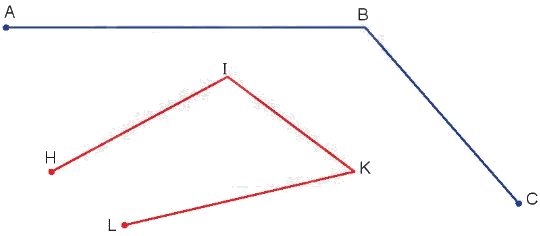
Phương pháp giải:
- Dùng thước để đo độ dài các đoạn thẳng AB, BC, HI, IK, KL.
- Độ dài đường gấp khúc ABC bằng tổng độ dài hai đoạn thẳng AB và BC.
- Độ dài đường gấp khúc HIKL bằng tổng độ dài ba đoạn thẳng HI, IK và KL.
Lời giải chi tiết:
Dùng thước đo ta có độ dài các đoạn thẳng như sau:
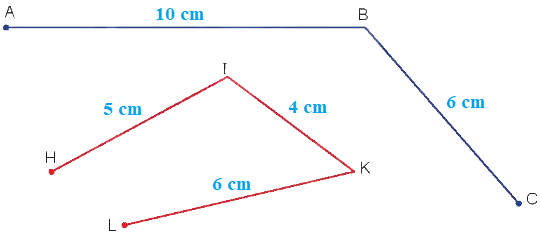
Độ dài đường gấp khúc ABC là:
10 cm + 6 cm = 16 cm
Độ dài đường gấp khúc HIKL là:
5 cm + 4 cm + 6 cm = 15 cm
Vậy: Đường gấp khúc ABC dài16 cm.
Đường gấp khúc HIKL dài15 cm.
Bài 1 (trang 52 SGK Toán 2 tập 1)
Xếp đường gấp khúc.

Phương pháp giải:
Em nhớ lại hình dạng của đường gấp khúc rồi tự xếp đường gấp khúc theo ý thích.
Lời giải chi tiết:
Ví dụ mẫu: Ta xếp 3 thước kẻ thành đường gấp khúc như sau:

Hoặc xếp 4 thước kẻ thàng đường gấp khúc:

Bài 1 (trang 52 SGK Toán 2 tập 1)
Xếp đường gấp khúc.

Phương pháp giải:
Em nhớ lại hình dạng của đường gấp khúc rồi tự xếp đường gấp khúc theo ý thích.
Lời giải chi tiết:
Ví dụ mẫu: Ta xếp 3 thước kẻ thành đường gấp khúc như sau:

Hoặc xếp 4 thước kẻ thàng đường gấp khúc:

Bài 1 (trang 53 SGK Toán 2 tập 1)
Nói theo mẫu.
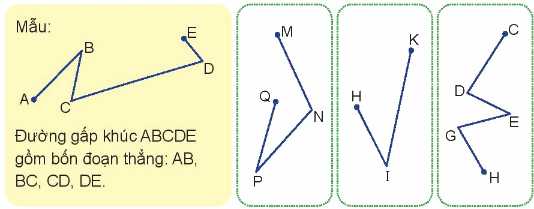
Phương pháp giải:
Quan sát hình vẽ để tìm các đoạn thẳng có trong mỗi đường gấp khúc và nói tương tự như mẫu đã cho.
Lời giải chi tiết:
- Đường gấp khúc MNPQ gồm ba đoạn thẳng: MN, NP, PQ.
- Đường gấp khúc HIK gồm hai đoạn thẳng: HI, IK.
- Đường gấp khúc CDEGH gồm bốn đoạn thẳng: CD, DE, EG, GH.
Đo rồi tính độ dài mỗi đường gấp khúc.
Đường gấp khúc ABC dài .?.cm.
Đường gấp khúc HIKL dài .?.cm.
Phương pháp giải:
- Dùng thước để đo độ dài các đoạn thẳng AB, BC, HI, IK, KL.
- Độ dài đường gấp khúc ABC bằng tổng độ dài hai đoạn thẳng AB và BC.
- Độ dài đường gấp khúc HIKL bằng tổng độ dài ba đoạn thẳng HI, IK và KL.
Lời giải chi tiết:
Dùng thước đo ta có độ dài các đoạn thẳng như sau:
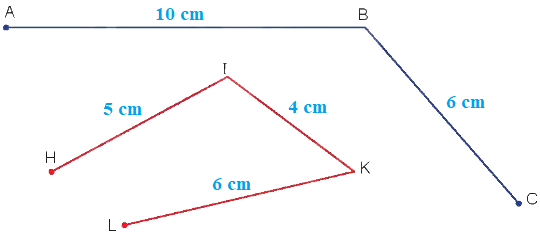
Độ dài đường gấp khúc ABC là:
10 cm + 6 cm = 16 cm
Độ dài đường gấp khúc HIKL là:
5 cm + 4 cm + 6 cm = 15 cm
Vậy: Đường gấp khúc ABC dài16 cm.
Đường gấp khúc HIKL dài15 cm.
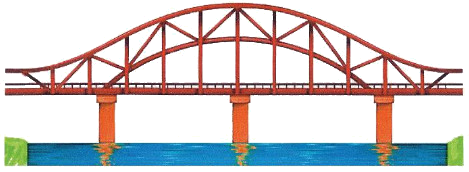
Tìm hình ảnh một đoạn thẳng, một đường cong và một đường gấp khúc trong hình vẽ sau.
Phương pháp giải:
- Nhớ lại hình dạng của đoạn thẳng, đường cong và đường gấp khúc.
- Quan sát hình vẽ và tìm hình ảnh của đoạn thẳng, một đường cong và một đường gấp khúc.
Lời giải chi tiết:
Ví dụ mẫu:
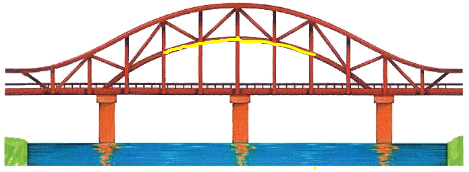
Hình ảnh của đoạn thẳng (được tô màu xanh da trời)
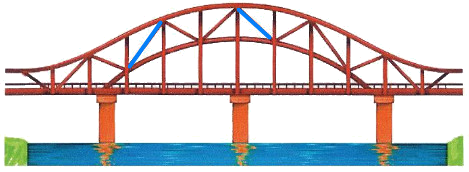
Hình ảnh của đường cong (được tô màu vàng):
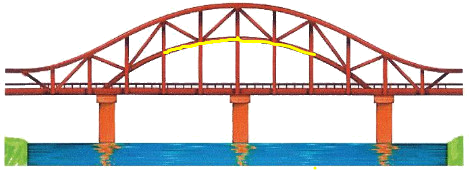
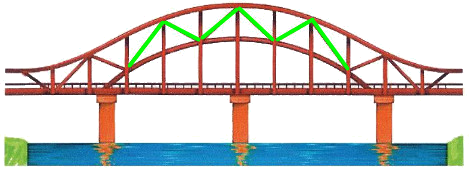
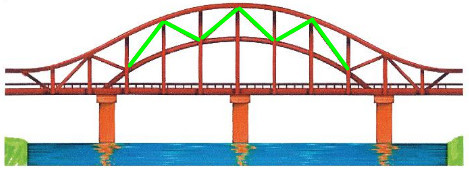
Hình ảnh đường gấp khúc (được tô màu xanh lá cây):
Tìm hình ảnh một đoạn thẳng, một đường cong và một đường gấp khúc trong hình vẽ sau.
Phương pháp giải:
- Nhớ lại hình dạng của đoạn thẳng, đường cong và đường gấp khúc.
- Quan sát hình vẽ và tìm hình ảnh của đoạn thẳng, một đường cong và một đường gấp khúc.
Lời giải chi tiết:
Ví dụ mẫu:
Hình ảnh của đoạn thẳng (được tô màu xanh da trời)
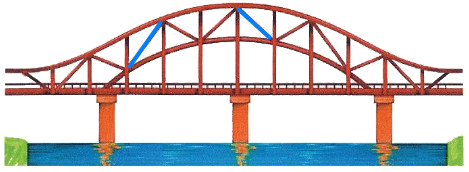
Hình ảnh của đường cong (được tô màu vàng):
Hình ảnh đường gấp khúc (được tô màu xanh lá cây):
Đường gấp khúc là một đường được tạo thành bởi hai hoặc nhiều đoạn thẳng liên tiếp. Các đoạn thẳng này được gọi là các cạnh của đường gấp khúc. Điểm nối giữa hai đoạn thẳng liên tiếp được gọi là đỉnh của đường gấp khúc.
Có nhiều loại đường gấp khúc khác nhau, tùy thuộc vào số lượng cạnh và vị trí của các đỉnh:
Để tính độ dài của một đường gấp khúc, ta cộng độ dài của tất cả các đoạn thẳng tạo thành đường gấp khúc đó.
Ví dụ: Nếu một đường gấp khúc có ba đoạn thẳng với độ dài lần lượt là 3cm, 5cm và 2cm, thì độ dài của đường gấp khúc đó là 3cm + 5cm + 2cm = 10cm.
Đường gấp khúc xuất hiện rất nhiều trong thực tế, ví dụ:
Dưới đây là một số bài tập về đường gấp khúc để bạn luyện tập:
Giải bài 1: Độ dài đường gấp khúc ABC là AB + BC = 50m + 30m = 80m.
Giải bài 2: (Tự vẽ và đo)
Giải bài 3: Đường đi ngắn nhất là đường chéo AC. Độ dài AC có thể tính bằng định lý Pitago: AC = √(102 + 52) = √125 ≈ 11.18m.
Ngoài những kiến thức cơ bản trên, bạn có thể tìm hiểu thêm về:
giaitoan.edu.vn cung cấp một nền tảng học toán online toàn diện, với các bài giảng được thiết kế bởi các giáo viên giàu kinh nghiệm. Chúng tôi cam kết mang đến cho bạn những kiến thức toán học chính xác, dễ hiểu và hiệu quả. Hãy truy cập giaitoan.edu.vn ngay hôm nay để bắt đầu hành trình khám phá thế giới toán học!