Chào mừng các em học sinh lớp 4 đến với bài trắc nghiệm Rút gọn phân số, thuộc Bài 56 chương trình Toán 4 Kết nối tri thức. Bài trắc nghiệm này được thiết kế để giúp các em ôn tập và củng cố kiến thức về cách rút gọn phân số, một kỹ năng quan trọng trong chương trình toán học.
Giaitoan.edu.vn cung cấp bộ đề trắc nghiệm đa dạng, với nhiều mức độ khó khác nhau, giúp các em tự đánh giá năng lực và tìm ra những điểm cần cải thiện.

Trong các phân số sau, phân số nào là phân số tối giản?
A. \(\dfrac{6}{9}\)
B. \(\dfrac{4}{7}\)
C. \(\dfrac{{20}}{{15}}\)
D. \(\dfrac{{15}}{{27}}\)

Rút gọn phân số sau thành phân số tối giản:

\(\dfrac{{4 \times 5 \times 7}}{{7 \times 5 \times 9}} = \dfrac{4}{9}\) . Đúng hay sai?
A. Đúng
B. Sai

Trong các phân số sau, phân số nào chưa tối giản:
$\frac{1}{7}$
$\frac{{21}}{{35}}$
$\frac{{97}}{{90}}$
$\frac{{81}}{4}$

Rút gọn phân số \(\dfrac{{72}}{{180}}\) ta được phân số tối giản là:
A. \(\dfrac{2}{5}\)
B. \(\dfrac{3}{5}\)
C. \(\dfrac{{18}}{{45}}\)
D. \(\dfrac{8}{{20}}\)

Trong các phân số sau phân số nào bằng phân số $\frac{{24}}{{120}}$
$\frac{{20}}{{100}}$
$\frac{4}{{25}}$
$\frac{4}{5}$
$\frac{7}{{28}}$

Phân số bằng với phân số \(\dfrac{{216}}{{360}}\) và có mẫu số bé nhất là phân số

Rút gọn phân số sau thành phân số tối giản:
Lời giải và đáp án

Trong các phân số sau, phân số nào là phân số tối giản?
A. \(\dfrac{6}{9}\)
B. \(\dfrac{4}{7}\)
C. \(\dfrac{{20}}{{15}}\)
D. \(\dfrac{{15}}{{27}}\)
B. \(\dfrac{4}{7}\)
- Rút gọn các phân số đã cho (nếu được)Phân số tối giản là phân số có tử số và mẫu số không cùng chia hết cho một số tự nhiên nào lớn hơn \(1\), hay phân số tối giản là phân số không thể rút gọn được nữa.
Ta có: \(\dfrac{6}{9} = \dfrac{{6:3}}{{9:3}} = \dfrac{2}{3}\,\,\,\, ;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{20}}{{15}} = \dfrac{{20:5}}{{15:5}} = \dfrac{4}{3}\,\,\, ;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{15}}{{27}} = \dfrac{{15:3}}{{27:3}} = \dfrac{5}{9}\)
Phân số \(\dfrac{4}{7}\) có tử số và mẫu số không cùng chia hết cho một số tự nhiên nào lớn hơn \(1\), nên \(\dfrac{4}{7}\) là phân số tối giản.
Vậy trong các phân số đã cho, phân số tối giản là phân số \(\dfrac{4}{7}\).

Rút gọn phân số sau thành phân số tối giản:
Ta thấy \(5\) và \(20\) cùng chia hết cho \(5\) nên ta chia cả tử số và mẫu số của phân số \(\dfrac{5}{{20}}\) cho \(5\).
Ta thấy \(5\) và \(20\) cùng chia hết cho \(5\) nên ta có:
\(\dfrac{5}{{20}} = \dfrac{{5:5}}{{20:5}} = \dfrac{1}{4}\)
Vậy đáp án đúng điền vào ô trống lần lượt từ trên xuống dưới là \(1\,;\,\,4\).

\(\dfrac{{4 \times 5 \times 7}}{{7 \times 5 \times 9}} = \dfrac{4}{9}\) . Đúng hay sai?
A. Đúng
B. Sai
A. Đúng
B. Sai
Tích ở tử số và mẫu số đều có thừa số chung là \(5\) và \(7\) nên ta cùng chia nhẩm tích ở tử số và mẫu số cho \(5\), rồi cùng chia nhẩm cho \(7\).
Ta có:
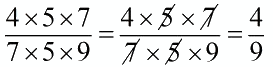
Vậy phép tính đã cho là đúng.

Trong các phân số sau, phân số nào chưa tối giản:
$\frac{1}{7}$
$\frac{{21}}{{35}}$
$\frac{{97}}{{90}}$
$\frac{{81}}{4}$
Đáp án : B
Phân số tối giản là phân số có tử số và mẫu số không cùng chia hết cho số tự nhiên nào lớn hơn 1.
Phân số chưa tối giản là $\frac{{21}}{{35}}$

Rút gọn phân số \(\dfrac{{72}}{{180}}\) ta được phân số tối giản là:
A. \(\dfrac{2}{5}\)
B. \(\dfrac{3}{5}\)
C. \(\dfrac{{18}}{{45}}\)
D. \(\dfrac{8}{{20}}\)
A. \(\dfrac{2}{5}\)
Khi rút gọn phân số có thể làm như sau:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn \(1\).
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản.
Ta thấy phân số \(\dfrac{{72}}{{180}}\) có tử số và mẫu số đều chia hết cho \(4\), nên ta có:
\(\dfrac{{72}}{{180}} = \dfrac{{72:4}}{{180:4}} = \dfrac{{18}}{{45}}\)
Ta thấy phân số \(\dfrac{{18}}{{45}}\) có tử số và mẫu số đều chia hết cho \(9\), nên ta có:
\(\dfrac{{18}}{{45}} = \dfrac{{18:9}}{{45:9}} = \dfrac{2}{5}\)
Ta thấy phân số \(\dfrac{2}{5}\) có tử số và mẫu số không cùng chia hết cho số tự nhiên nào lớn hơn \(1\) nên \(\dfrac{2}{5}\) là phân số tối giản.
Vậy \(\dfrac{{72}}{{180}} = \dfrac{2}{5}\).

Trong các phân số sau phân số nào bằng phân số $\frac{{24}}{{120}}$
$\frac{{20}}{{100}}$
$\frac{4}{{25}}$
$\frac{4}{5}$
$\frac{7}{{28}}$
Đáp án : A
Rút gọn phân số đã cho để trả lời câu hỏi của bài toán
Ta có $\frac{{24}}{{120}} = \frac{1}{5} = \frac{{20}}{{100}}$

Phân số bằng với phân số \(\dfrac{{216}}{{360}}\) và có mẫu số bé nhất là phân số
Phân số bằng với phân số \(\dfrac{{216}}{{360}}\) và có mẫu số bé nhất chính là phân số tối giản sau khi rút gọn phân số \(\dfrac{{216}}{{360}}\).
Phân số cần tìm bằng phân số \(\dfrac{{216}}{{360}}\) và có mẫu số bé nhất chính là phân số tối giản sau khi rút gọn phân số \(\dfrac{{216}}{{360}}\).
Rút gọn phân số \(\dfrac{{216}}{{360}}\) để được phân số tối giản, ta có:
\(\begin{array}{l}\dfrac{{216}}{{360}} = \dfrac{{216:4}}{{360:4}} = \dfrac{{54}}{{90}}\\\dfrac{{54}}{{90}} = \dfrac{{54:9}}{{90:9}} = \dfrac{6}{{10}}\\\dfrac{6}{{10}} = \dfrac{{6:2}}{{10:2}} = \dfrac{3}{5}\end{array}\)
Ta thấy phân số \(\dfrac{3}{5}\) có tử số và mẫu số không cùng chia hết cho số tự nhiên nào lớn hơn \(1\) nên \(\dfrac{3}{5}\) là phân số tối giản.
Do đó, phân số bằng với phân số \(\dfrac{{216}}{{360}}\) và có mẫu số bé nhất là phân số \(\dfrac{3}{5}\).
Vậy đáp án đúng điền vào ô trống lần lượt từ trên xuống dưới là \(3\,;\,\,5\).

Rút gọn phân số sau thành phân số tối giản:
Phân tích tử số và mẫu số thành tích của các thừa số, sau đó chia nhẩm tích ở tử số và mẫu số cho các thừa số chung.
Tách \(44\) thành tích của \(11\) và \(4\), tách \(33\) thành tích của \(11\) và \(3\) , tách \(45\) thành tích của \(9\) và \(5\) , ta có:
\(\dfrac{{2 \times 9 \times 44}}{{33 \times 45 \times 7}} = \dfrac{{2 \times 9 \times 11 \times 4}}{{11 \times 3 \times 9 \times 5 \times 7}}\)
Ta thấy tích ở trên gạch ngang và tích ở dưới gạch ngang đều có chung các thừa số là \(9\) và \(11\).
Cùng chia nhẩm tích ở trên gạch ngang và tích ở dưới gạch ngang cho \(9\) và \(11\) ta được: \(\dfrac{{2 \times 9 \times 44}}{{33 \times 45 \times 7}} = \dfrac{{2 \times 9 \times 11 \times 4}}{{11 \times 3 \times 9 \times 5 \times 7}} = \dfrac{{2 \times 4}}{{3 \times 5 \times 7}} = \dfrac{8}{{105}}\)
Mà \(\dfrac{8}{{105}}\) là phân số tối giản vì có tử số và mẫu số không cùng chia hết cho số tự nhiên nào khác \(1\).
Vậy \(\dfrac{{2 \times 9 \times 44}}{{33 \times 45 \times 7}} = \dfrac{8}{{105}}\)
Đáp án đúng điền vào ô trống lần lượt từ trên xuống dưới là \(8\,;\,\,105\).

Trong các phân số sau, phân số nào là phân số tối giản?
A. \(\dfrac{6}{9}\)
B. \(\dfrac{4}{7}\)
C. \(\dfrac{{20}}{{15}}\)
D. \(\dfrac{{15}}{{27}}\)

Rút gọn phân số sau thành phân số tối giản:

\(\dfrac{{4 \times 5 \times 7}}{{7 \times 5 \times 9}} = \dfrac{4}{9}\) . Đúng hay sai?
A. Đúng
B. Sai

Trong các phân số sau, phân số nào chưa tối giản:
$\frac{1}{7}$
$\frac{{21}}{{35}}$
$\frac{{97}}{{90}}$
$\frac{{81}}{4}$

Rút gọn phân số \(\dfrac{{72}}{{180}}\) ta được phân số tối giản là:
A. \(\dfrac{2}{5}\)
B. \(\dfrac{3}{5}\)
C. \(\dfrac{{18}}{{45}}\)
D. \(\dfrac{8}{{20}}\)

Trong các phân số sau phân số nào bằng phân số $\frac{{24}}{{120}}$
$\frac{{20}}{{100}}$
$\frac{4}{{25}}$
$\frac{4}{5}$
$\frac{7}{{28}}$

Phân số bằng với phân số \(\dfrac{{216}}{{360}}\) và có mẫu số bé nhất là phân số

Rút gọn phân số sau thành phân số tối giản:

Trong các phân số sau, phân số nào là phân số tối giản?
A. \(\dfrac{6}{9}\)
B. \(\dfrac{4}{7}\)
C. \(\dfrac{{20}}{{15}}\)
D. \(\dfrac{{15}}{{27}}\)
B. \(\dfrac{4}{7}\)
- Rút gọn các phân số đã cho (nếu được)Phân số tối giản là phân số có tử số và mẫu số không cùng chia hết cho một số tự nhiên nào lớn hơn \(1\), hay phân số tối giản là phân số không thể rút gọn được nữa.
Ta có: \(\dfrac{6}{9} = \dfrac{{6:3}}{{9:3}} = \dfrac{2}{3}\,\,\,\, ;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{20}}{{15}} = \dfrac{{20:5}}{{15:5}} = \dfrac{4}{3}\,\,\, ;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{15}}{{27}} = \dfrac{{15:3}}{{27:3}} = \dfrac{5}{9}\)
Phân số \(\dfrac{4}{7}\) có tử số và mẫu số không cùng chia hết cho một số tự nhiên nào lớn hơn \(1\), nên \(\dfrac{4}{7}\) là phân số tối giản.
Vậy trong các phân số đã cho, phân số tối giản là phân số \(\dfrac{4}{7}\).

Rút gọn phân số sau thành phân số tối giản:
Ta thấy \(5\) và \(20\) cùng chia hết cho \(5\) nên ta chia cả tử số và mẫu số của phân số \(\dfrac{5}{{20}}\) cho \(5\).
Ta thấy \(5\) và \(20\) cùng chia hết cho \(5\) nên ta có:
\(\dfrac{5}{{20}} = \dfrac{{5:5}}{{20:5}} = \dfrac{1}{4}\)
Vậy đáp án đúng điền vào ô trống lần lượt từ trên xuống dưới là \(1\,;\,\,4\).

\(\dfrac{{4 \times 5 \times 7}}{{7 \times 5 \times 9}} = \dfrac{4}{9}\) . Đúng hay sai?
A. Đúng
B. Sai
A. Đúng
B. Sai
Tích ở tử số và mẫu số đều có thừa số chung là \(5\) và \(7\) nên ta cùng chia nhẩm tích ở tử số và mẫu số cho \(5\), rồi cùng chia nhẩm cho \(7\).
Ta có:
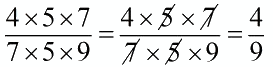
Vậy phép tính đã cho là đúng.

Trong các phân số sau, phân số nào chưa tối giản:
$\frac{1}{7}$
$\frac{{21}}{{35}}$
$\frac{{97}}{{90}}$
$\frac{{81}}{4}$
Đáp án : B
Phân số tối giản là phân số có tử số và mẫu số không cùng chia hết cho số tự nhiên nào lớn hơn 1.
Phân số chưa tối giản là $\frac{{21}}{{35}}$

Rút gọn phân số \(\dfrac{{72}}{{180}}\) ta được phân số tối giản là:
A. \(\dfrac{2}{5}\)
B. \(\dfrac{3}{5}\)
C. \(\dfrac{{18}}{{45}}\)
D. \(\dfrac{8}{{20}}\)
A. \(\dfrac{2}{5}\)
Khi rút gọn phân số có thể làm như sau:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn \(1\).
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản.
Ta thấy phân số \(\dfrac{{72}}{{180}}\) có tử số và mẫu số đều chia hết cho \(4\), nên ta có:
\(\dfrac{{72}}{{180}} = \dfrac{{72:4}}{{180:4}} = \dfrac{{18}}{{45}}\)
Ta thấy phân số \(\dfrac{{18}}{{45}}\) có tử số và mẫu số đều chia hết cho \(9\), nên ta có:
\(\dfrac{{18}}{{45}} = \dfrac{{18:9}}{{45:9}} = \dfrac{2}{5}\)
Ta thấy phân số \(\dfrac{2}{5}\) có tử số và mẫu số không cùng chia hết cho số tự nhiên nào lớn hơn \(1\) nên \(\dfrac{2}{5}\) là phân số tối giản.
Vậy \(\dfrac{{72}}{{180}} = \dfrac{2}{5}\).

Trong các phân số sau phân số nào bằng phân số $\frac{{24}}{{120}}$
$\frac{{20}}{{100}}$
$\frac{4}{{25}}$
$\frac{4}{5}$
$\frac{7}{{28}}$
Đáp án : A
Rút gọn phân số đã cho để trả lời câu hỏi của bài toán
Ta có $\frac{{24}}{{120}} = \frac{1}{5} = \frac{{20}}{{100}}$

Phân số bằng với phân số \(\dfrac{{216}}{{360}}\) và có mẫu số bé nhất là phân số
Phân số bằng với phân số \(\dfrac{{216}}{{360}}\) và có mẫu số bé nhất chính là phân số tối giản sau khi rút gọn phân số \(\dfrac{{216}}{{360}}\).
Phân số cần tìm bằng phân số \(\dfrac{{216}}{{360}}\) và có mẫu số bé nhất chính là phân số tối giản sau khi rút gọn phân số \(\dfrac{{216}}{{360}}\).
Rút gọn phân số \(\dfrac{{216}}{{360}}\) để được phân số tối giản, ta có:
\(\begin{array}{l}\dfrac{{216}}{{360}} = \dfrac{{216:4}}{{360:4}} = \dfrac{{54}}{{90}}\\\dfrac{{54}}{{90}} = \dfrac{{54:9}}{{90:9}} = \dfrac{6}{{10}}\\\dfrac{6}{{10}} = \dfrac{{6:2}}{{10:2}} = \dfrac{3}{5}\end{array}\)
Ta thấy phân số \(\dfrac{3}{5}\) có tử số và mẫu số không cùng chia hết cho số tự nhiên nào lớn hơn \(1\) nên \(\dfrac{3}{5}\) là phân số tối giản.
Do đó, phân số bằng với phân số \(\dfrac{{216}}{{360}}\) và có mẫu số bé nhất là phân số \(\dfrac{3}{5}\).
Vậy đáp án đúng điền vào ô trống lần lượt từ trên xuống dưới là \(3\,;\,\,5\).

Rút gọn phân số sau thành phân số tối giản:
Phân tích tử số và mẫu số thành tích của các thừa số, sau đó chia nhẩm tích ở tử số và mẫu số cho các thừa số chung.
Tách \(44\) thành tích của \(11\) và \(4\), tách \(33\) thành tích của \(11\) và \(3\) , tách \(45\) thành tích của \(9\) và \(5\) , ta có:
\(\dfrac{{2 \times 9 \times 44}}{{33 \times 45 \times 7}} = \dfrac{{2 \times 9 \times 11 \times 4}}{{11 \times 3 \times 9 \times 5 \times 7}}\)
Ta thấy tích ở trên gạch ngang và tích ở dưới gạch ngang đều có chung các thừa số là \(9\) và \(11\).
Cùng chia nhẩm tích ở trên gạch ngang và tích ở dưới gạch ngang cho \(9\) và \(11\) ta được: \(\dfrac{{2 \times 9 \times 44}}{{33 \times 45 \times 7}} = \dfrac{{2 \times 9 \times 11 \times 4}}{{11 \times 3 \times 9 \times 5 \times 7}} = \dfrac{{2 \times 4}}{{3 \times 5 \times 7}} = \dfrac{8}{{105}}\)
Mà \(\dfrac{8}{{105}}\) là phân số tối giản vì có tử số và mẫu số không cùng chia hết cho số tự nhiên nào khác \(1\).
Vậy \(\dfrac{{2 \times 9 \times 44}}{{33 \times 45 \times 7}} = \dfrac{8}{{105}}\)
Đáp án đúng điền vào ô trống lần lượt từ trên xuống dưới là \(8\,;\,\,105\).
Bài 56 trong chương trình Toán 4 Kết nối tri thức tập trung vào việc giúp học sinh nắm vững phương pháp rút gọn phân số. Đây là một kỹ năng cơ bản nhưng vô cùng quan trọng, là nền tảng cho các phép toán phức tạp hơn về phân số trong các lớp học tiếp theo. Việc rút gọn phân số không chỉ giúp biểu diễn phân số một cách đơn giản hơn mà còn giúp so sánh và thực hiện các phép tính trên phân số dễ dàng hơn.
Rút gọn phân số là việc chia cả tử số và mẫu số của phân số cho một ước chung lớn nhất của chúng. Kết quả là một phân số mới tương đương với phân số ban đầu nhưng có tử số và mẫu số nhỏ hơn. Để rút gọn phân số, chúng ta cần tìm ước chung lớn nhất (UCLN) của tử số và mẫu số. UCLN là số lớn nhất mà cả tử số và mẫu số đều chia hết.
Ví dụ 1: Rút gọn phân số 12/18
Ví dụ 2: Rút gọn phân số 25/35
Dưới đây là một số dạng bài tập trắc nghiệm thường gặp trong bài học Rút gọn phân số:
Việc rút gọn phân số có nhiều ứng dụng trong thực tế, ví dụ như:
Bài học Rút gọn phân số Toán 4 Kết nối tri thức là một bước quan trọng trong việc xây dựng nền tảng toán học vững chắc cho các em học sinh. Hy vọng rằng với những kiến thức và bài tập đã được cung cấp, các em sẽ tự tin hơn trong việc giải quyết các bài toán liên quan đến phân số. Hãy luyện tập thường xuyên để nắm vững kiến thức và đạt kết quả tốt nhất!