Bài 59 thuộc chương trình Toán 4 Cánh diều tập trung vào kỹ năng rút gọn phân số - một trong những kiến thức cơ bản và quan trọng của toán học. Việc nắm vững phương pháp rút gọn phân số không chỉ giúp học sinh giải quyết các bài toán một cách nhanh chóng và chính xác mà còn là bước đệm quan trọng cho các kiến thức nâng cao hơn.
Tại giaitoan.edu.vn, chúng tôi cung cấp bộ trắc nghiệm Bài 59: Rút gọn phân số Toán 4 Cánh diều được thiết kế khoa học, đa dạng các dạng bài tập, giúp học sinh củng cố kiến thức và rèn luyện kỹ năng một cách hiệu quả.

Trong các phân số sau, phân số nào là phân số tối giản?
A. \(\dfrac{6}{9}\)
B. \(\dfrac{4}{7}\)
C. \(\dfrac{{20}}{{15}}\)
D. \(\dfrac{{15}}{{27}}\)

Rút gọn phân số sau thành phân số tối giản:

\(\dfrac{{4 \times 5 \times 7}}{{7 \times 5 \times 9}} = \dfrac{4}{9}\) . Đúng hay sai?
A. Đúng
B. Sai

Trong các phân số sau, phân số nào chưa tối giản:
$\frac{1}{7}$
$\frac{{21}}{{35}}$
$\frac{{97}}{{90}}$
$\frac{{81}}{4}$

Trong các phân số sau phân số nào bằng phân số $\frac{{24}}{{120}}$
$\frac{{20}}{{100}}$
$\frac{4}{{25}}$
$\frac{4}{5}$
$\frac{7}{{28}}$

Rút gọn phân số \(\dfrac{{72}}{{180}}\) ta được phân số tối giản là:
A. \(\dfrac{2}{5}\)
B. \(\dfrac{3}{5}\)
C. \(\dfrac{{18}}{{45}}\)
D. \(\dfrac{8}{{20}}\)

Rút gọn phân số sau thành phân số tối giản:

Phân số bằng với phân số \(\dfrac{{216}}{{360}}\) và có mẫu số bé nhất là phân số
Lời giải và đáp án

Trong các phân số sau, phân số nào là phân số tối giản?
A. \(\dfrac{6}{9}\)
B. \(\dfrac{4}{7}\)
C. \(\dfrac{{20}}{{15}}\)
D. \(\dfrac{{15}}{{27}}\)
B. \(\dfrac{4}{7}\)
- Rút gọn các phân số đã cho (nếu được)Phân số tối giản là phân số có tử số và mẫu số không cùng chia hết cho một số tự nhiên nào lớn hơn \(1\), hay phân số tối giản là phân số không thể rút gọn được nữa.
Ta có: \(\dfrac{6}{9} = \dfrac{{6:3}}{{9:3}} = \dfrac{2}{3}\,\,\,\, ;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{20}}{{15}} = \dfrac{{20:5}}{{15:5}} = \dfrac{4}{3}\,\,\, ;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{15}}{{27}} = \dfrac{{15:3}}{{27:3}} = \dfrac{5}{9}\)
Phân số \(\dfrac{4}{7}\) có tử số và mẫu số không cùng chia hết cho một số tự nhiên nào lớn hơn \(1\), nên \(\dfrac{4}{7}\) là phân số tối giản.
Vậy trong các phân số đã cho, phân số tối giản là phân số \(\dfrac{4}{7}\).

Rút gọn phân số sau thành phân số tối giản:
Ta thấy \(5\) và \(20\) cùng chia hết cho \(5\) nên ta chia cả tử số và mẫu số của phân số \(\dfrac{5}{{20}}\) cho \(5\).
Ta thấy \(5\) và \(20\) cùng chia hết cho \(5\) nên ta có:
\(\dfrac{5}{{20}} = \dfrac{{5:5}}{{20:5}} = \dfrac{1}{4}\)
Vậy đáp án đúng điền vào ô trống lần lượt từ trên xuống dưới là \(1\,;\,\,4\).

\(\dfrac{{4 \times 5 \times 7}}{{7 \times 5 \times 9}} = \dfrac{4}{9}\) . Đúng hay sai?
A. Đúng
B. Sai
A. Đúng
B. Sai
Tích ở tử số và mẫu số đều có thừa số chung là \(5\) và \(7\) nên ta cùng chia nhẩm tích ở tử số và mẫu số cho \(5\), rồi cùng chia nhẩm cho \(7\).
Ta có:
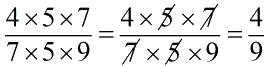
Vậy phép tính đã cho là đúng.

Trong các phân số sau, phân số nào chưa tối giản:
$\frac{1}{7}$
$\frac{{21}}{{35}}$
$\frac{{97}}{{90}}$
$\frac{{81}}{4}$
Đáp án : B
Phân số tối giản là phân số có tử số và mẫu số không cùng chia hết cho số tự nhiên nào lớn hơn 1.
Phân số chưa tối giản là $\frac{{21}}{{35}}$

Trong các phân số sau phân số nào bằng phân số $\frac{{24}}{{120}}$
$\frac{{20}}{{100}}$
$\frac{4}{{25}}$
$\frac{4}{5}$
$\frac{7}{{28}}$
Đáp án : A
Rút gọn phân số đã cho để trả lời câu hỏi của bài toán
Ta có $\frac{{24}}{{120}} = \frac{1}{5} = \frac{{20}}{{100}}$

Rút gọn phân số \(\dfrac{{72}}{{180}}\) ta được phân số tối giản là:
A. \(\dfrac{2}{5}\)
B. \(\dfrac{3}{5}\)
C. \(\dfrac{{18}}{{45}}\)
D. \(\dfrac{8}{{20}}\)
A. \(\dfrac{2}{5}\)
Khi rút gọn phân số có thể làm như sau:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn \(1\).
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản.
Ta thấy phân số \(\dfrac{{72}}{{180}}\) có tử số và mẫu số đều chia hết cho \(4\), nên ta có:
\(\dfrac{{72}}{{180}} = \dfrac{{72:4}}{{180:4}} = \dfrac{{18}}{{45}}\)
Ta thấy phân số \(\dfrac{{18}}{{45}}\) có tử số và mẫu số đều chia hết cho \(9\), nên ta có:
\(\dfrac{{18}}{{45}} = \dfrac{{18:9}}{{45:9}} = \dfrac{2}{5}\)
Ta thấy phân số \(\dfrac{2}{5}\) có tử số và mẫu số không cùng chia hết cho số tự nhiên nào lớn hơn \(1\) nên \(\dfrac{2}{5}\) là phân số tối giản.
Vậy \(\dfrac{{72}}{{180}} = \dfrac{2}{5}\).

Rút gọn phân số sau thành phân số tối giản:
Phân tích tử số và mẫu số thành tích của các thừa số, sau đó chia nhẩm tích ở tử số và mẫu số cho các thừa số chung.
Tách \(44\) thành tích của \(11\) và \(4\), tách \(33\) thành tích của \(11\) và \(3\) , tách \(45\) thành tích của \(9\) và \(5\) , ta có:
\(\dfrac{{2 \times 9 \times 44}}{{33 \times 45 \times 7}} = \dfrac{{2 \times 9 \times 11 \times 4}}{{11 \times 3 \times 9 \times 5 \times 7}}\)
Ta thấy tích ở trên gạch ngang và tích ở dưới gạch ngang đều có chung các thừa số là \(9\) và \(11\).
Cùng chia nhẩm tích ở trên gạch ngang và tích ở dưới gạch ngang cho \(9\) và \(11\) ta được: \(\dfrac{{2 \times 9 \times 44}}{{33 \times 45 \times 7}} = \dfrac{{2 \times 9 \times 11 \times 4}}{{11 \times 3 \times 9 \times 5 \times 7}} = \dfrac{{2 \times 4}}{{3 \times 5 \times 7}} = \dfrac{8}{{105}}\)
Mà \(\dfrac{8}{{105}}\) là phân số tối giản vì có tử số và mẫu số không cùng chia hết cho số tự nhiên nào khác \(1\).
Vậy \(\dfrac{{2 \times 9 \times 44}}{{33 \times 45 \times 7}} = \dfrac{8}{{105}}\)
Đáp án đúng điền vào ô trống lần lượt từ trên xuống dưới là \(8\,;\,\,105\).

Phân số bằng với phân số \(\dfrac{{216}}{{360}}\) và có mẫu số bé nhất là phân số
Phân số bằng với phân số \(\dfrac{{216}}{{360}}\) và có mẫu số bé nhất chính là phân số tối giản sau khi rút gọn phân số \(\dfrac{{216}}{{360}}\).
Phân số cần tìm bằng phân số \(\dfrac{{216}}{{360}}\) và có mẫu số bé nhất chính là phân số tối giản sau khi rút gọn phân số \(\dfrac{{216}}{{360}}\).
Rút gọn phân số \(\dfrac{{216}}{{360}}\) để được phân số tối giản, ta có:
\(\begin{array}{l}\dfrac{{216}}{{360}} = \dfrac{{216:4}}{{360:4}} = \dfrac{{54}}{{90}}\\\dfrac{{54}}{{90}} = \dfrac{{54:9}}{{90:9}} = \dfrac{6}{{10}}\\\dfrac{6}{{10}} = \dfrac{{6:2}}{{10:2}} = \dfrac{3}{5}\end{array}\)
Ta thấy phân số \(\dfrac{3}{5}\) có tử số và mẫu số không cùng chia hết cho số tự nhiên nào lớn hơn \(1\) nên \(\dfrac{3}{5}\) là phân số tối giản.
Do đó, phân số bằng với phân số \(\dfrac{{216}}{{360}}\) và có mẫu số bé nhất là phân số \(\dfrac{3}{5}\).
Vậy đáp án đúng điền vào ô trống lần lượt từ trên xuống dưới là \(3\,;\,\,5\).

Trong các phân số sau, phân số nào là phân số tối giản?
A. \(\dfrac{6}{9}\)
B. \(\dfrac{4}{7}\)
C. \(\dfrac{{20}}{{15}}\)
D. \(\dfrac{{15}}{{27}}\)

Rút gọn phân số sau thành phân số tối giản:

\(\dfrac{{4 \times 5 \times 7}}{{7 \times 5 \times 9}} = \dfrac{4}{9}\) . Đúng hay sai?
A. Đúng
B. Sai

Trong các phân số sau, phân số nào chưa tối giản:
$\frac{1}{7}$
$\frac{{21}}{{35}}$
$\frac{{97}}{{90}}$
$\frac{{81}}{4}$

Trong các phân số sau phân số nào bằng phân số $\frac{{24}}{{120}}$
$\frac{{20}}{{100}}$
$\frac{4}{{25}}$
$\frac{4}{5}$
$\frac{7}{{28}}$

Rút gọn phân số \(\dfrac{{72}}{{180}}\) ta được phân số tối giản là:
A. \(\dfrac{2}{5}\)
B. \(\dfrac{3}{5}\)
C. \(\dfrac{{18}}{{45}}\)
D. \(\dfrac{8}{{20}}\)

Rút gọn phân số sau thành phân số tối giản:

Phân số bằng với phân số \(\dfrac{{216}}{{360}}\) và có mẫu số bé nhất là phân số

Trong các phân số sau, phân số nào là phân số tối giản?
A. \(\dfrac{6}{9}\)
B. \(\dfrac{4}{7}\)
C. \(\dfrac{{20}}{{15}}\)
D. \(\dfrac{{15}}{{27}}\)
B. \(\dfrac{4}{7}\)
- Rút gọn các phân số đã cho (nếu được)Phân số tối giản là phân số có tử số và mẫu số không cùng chia hết cho một số tự nhiên nào lớn hơn \(1\), hay phân số tối giản là phân số không thể rút gọn được nữa.
Ta có: \(\dfrac{6}{9} = \dfrac{{6:3}}{{9:3}} = \dfrac{2}{3}\,\,\,\, ;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{20}}{{15}} = \dfrac{{20:5}}{{15:5}} = \dfrac{4}{3}\,\,\, ;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{15}}{{27}} = \dfrac{{15:3}}{{27:3}} = \dfrac{5}{9}\)
Phân số \(\dfrac{4}{7}\) có tử số và mẫu số không cùng chia hết cho một số tự nhiên nào lớn hơn \(1\), nên \(\dfrac{4}{7}\) là phân số tối giản.
Vậy trong các phân số đã cho, phân số tối giản là phân số \(\dfrac{4}{7}\).

Rút gọn phân số sau thành phân số tối giản:
Ta thấy \(5\) và \(20\) cùng chia hết cho \(5\) nên ta chia cả tử số và mẫu số của phân số \(\dfrac{5}{{20}}\) cho \(5\).
Ta thấy \(5\) và \(20\) cùng chia hết cho \(5\) nên ta có:
\(\dfrac{5}{{20}} = \dfrac{{5:5}}{{20:5}} = \dfrac{1}{4}\)
Vậy đáp án đúng điền vào ô trống lần lượt từ trên xuống dưới là \(1\,;\,\,4\).

\(\dfrac{{4 \times 5 \times 7}}{{7 \times 5 \times 9}} = \dfrac{4}{9}\) . Đúng hay sai?
A. Đúng
B. Sai
A. Đúng
B. Sai
Tích ở tử số và mẫu số đều có thừa số chung là \(5\) và \(7\) nên ta cùng chia nhẩm tích ở tử số và mẫu số cho \(5\), rồi cùng chia nhẩm cho \(7\).
Ta có:
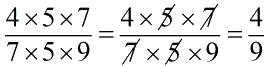
Vậy phép tính đã cho là đúng.

Trong các phân số sau, phân số nào chưa tối giản:
$\frac{1}{7}$
$\frac{{21}}{{35}}$
$\frac{{97}}{{90}}$
$\frac{{81}}{4}$
Đáp án : B
Phân số tối giản là phân số có tử số và mẫu số không cùng chia hết cho số tự nhiên nào lớn hơn 1.
Phân số chưa tối giản là $\frac{{21}}{{35}}$

Trong các phân số sau phân số nào bằng phân số $\frac{{24}}{{120}}$
$\frac{{20}}{{100}}$
$\frac{4}{{25}}$
$\frac{4}{5}$
$\frac{7}{{28}}$
Đáp án : A
Rút gọn phân số đã cho để trả lời câu hỏi của bài toán
Ta có $\frac{{24}}{{120}} = \frac{1}{5} = \frac{{20}}{{100}}$

Rút gọn phân số \(\dfrac{{72}}{{180}}\) ta được phân số tối giản là:
A. \(\dfrac{2}{5}\)
B. \(\dfrac{3}{5}\)
C. \(\dfrac{{18}}{{45}}\)
D. \(\dfrac{8}{{20}}\)
A. \(\dfrac{2}{5}\)
Khi rút gọn phân số có thể làm như sau:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn \(1\).
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản.
Ta thấy phân số \(\dfrac{{72}}{{180}}\) có tử số và mẫu số đều chia hết cho \(4\), nên ta có:
\(\dfrac{{72}}{{180}} = \dfrac{{72:4}}{{180:4}} = \dfrac{{18}}{{45}}\)
Ta thấy phân số \(\dfrac{{18}}{{45}}\) có tử số và mẫu số đều chia hết cho \(9\), nên ta có:
\(\dfrac{{18}}{{45}} = \dfrac{{18:9}}{{45:9}} = \dfrac{2}{5}\)
Ta thấy phân số \(\dfrac{2}{5}\) có tử số và mẫu số không cùng chia hết cho số tự nhiên nào lớn hơn \(1\) nên \(\dfrac{2}{5}\) là phân số tối giản.
Vậy \(\dfrac{{72}}{{180}} = \dfrac{2}{5}\).

Rút gọn phân số sau thành phân số tối giản:
Phân tích tử số và mẫu số thành tích của các thừa số, sau đó chia nhẩm tích ở tử số và mẫu số cho các thừa số chung.
Tách \(44\) thành tích của \(11\) và \(4\), tách \(33\) thành tích của \(11\) và \(3\) , tách \(45\) thành tích của \(9\) và \(5\) , ta có:
\(\dfrac{{2 \times 9 \times 44}}{{33 \times 45 \times 7}} = \dfrac{{2 \times 9 \times 11 \times 4}}{{11 \times 3 \times 9 \times 5 \times 7}}\)
Ta thấy tích ở trên gạch ngang và tích ở dưới gạch ngang đều có chung các thừa số là \(9\) và \(11\).
Cùng chia nhẩm tích ở trên gạch ngang và tích ở dưới gạch ngang cho \(9\) và \(11\) ta được: \(\dfrac{{2 \times 9 \times 44}}{{33 \times 45 \times 7}} = \dfrac{{2 \times 9 \times 11 \times 4}}{{11 \times 3 \times 9 \times 5 \times 7}} = \dfrac{{2 \times 4}}{{3 \times 5 \times 7}} = \dfrac{8}{{105}}\)
Mà \(\dfrac{8}{{105}}\) là phân số tối giản vì có tử số và mẫu số không cùng chia hết cho số tự nhiên nào khác \(1\).
Vậy \(\dfrac{{2 \times 9 \times 44}}{{33 \times 45 \times 7}} = \dfrac{8}{{105}}\)
Đáp án đúng điền vào ô trống lần lượt từ trên xuống dưới là \(8\,;\,\,105\).

Phân số bằng với phân số \(\dfrac{{216}}{{360}}\) và có mẫu số bé nhất là phân số
Phân số bằng với phân số \(\dfrac{{216}}{{360}}\) và có mẫu số bé nhất chính là phân số tối giản sau khi rút gọn phân số \(\dfrac{{216}}{{360}}\).
Phân số cần tìm bằng phân số \(\dfrac{{216}}{{360}}\) và có mẫu số bé nhất chính là phân số tối giản sau khi rút gọn phân số \(\dfrac{{216}}{{360}}\).
Rút gọn phân số \(\dfrac{{216}}{{360}}\) để được phân số tối giản, ta có:
\(\begin{array}{l}\dfrac{{216}}{{360}} = \dfrac{{216:4}}{{360:4}} = \dfrac{{54}}{{90}}\\\dfrac{{54}}{{90}} = \dfrac{{54:9}}{{90:9}} = \dfrac{6}{{10}}\\\dfrac{6}{{10}} = \dfrac{{6:2}}{{10:2}} = \dfrac{3}{5}\end{array}\)
Ta thấy phân số \(\dfrac{3}{5}\) có tử số và mẫu số không cùng chia hết cho số tự nhiên nào lớn hơn \(1\) nên \(\dfrac{3}{5}\) là phân số tối giản.
Do đó, phân số bằng với phân số \(\dfrac{{216}}{{360}}\) và có mẫu số bé nhất là phân số \(\dfrac{3}{5}\).
Vậy đáp án đúng điền vào ô trống lần lượt từ trên xuống dưới là \(3\,;\,\,5\).
Bài 59 trong sách Toán 4 Cánh diều tập trung vào việc củng cố kỹ năng rút gọn phân số. Rút gọn phân số là việc chia cả tử số và mẫu số của phân số cho ước chung lớn nhất (ƯCLN) của chúng. Việc này giúp biểu diễn phân số ở dạng đơn giản nhất, dễ hiểu và dễ so sánh hơn.
Ví dụ: Rút gọn phân số 12/18.
Các bài tập trắc nghiệm về rút gọn phân số thường bao gồm các dạng sau:
Luyện tập trắc nghiệm giúp học sinh:
Để giải nhanh các bài tập rút gọn phân số, học sinh có thể áp dụng một số mẹo sau:
Việc rút gọn phân số không chỉ quan trọng trong toán học mà còn có ứng dụng trong thực tế, ví dụ như:
Trắc nghiệm Bài 59: Rút gọn phân số Toán 4 Cánh diều là một phần quan trọng trong chương trình học. Việc luyện tập thường xuyên và nắm vững các kiến thức cơ bản sẽ giúp học sinh đạt kết quả tốt trong môn Toán. giaitoan.edu.vn hy vọng bộ trắc nghiệm này sẽ là công cụ hữu ích giúp các em học sinh học tập hiệu quả hơn.