Chào mừng các em học sinh đến với bài trắc nghiệm Bài 68: Đề-xi-mét vuông môn Toán lớp 4, sách Cánh diều. Bài trắc nghiệm này được thiết kế để giúp các em ôn tập và củng cố kiến thức về đơn vị diện tích đề-xi-mét vuông, cách đo diện tích hình vuông và hình chữ nhật.
Giaitoan.edu.vn hy vọng với bộ câu hỏi này, các em sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt nhất!

Đề-xi-mét vuông được kí hiệu là:
A. \(c{m^2}\)
B. \(d{m^2}\)
C. \({m^2}\)
D. \(m{m^2}\)

Điền số thích hợp vào ô trống:
\(3 d{m^2} =\)
\(\,c{m^2}\)

Điền số thích hợp vào ô trống:
\(12{m^2} =\)
\(d{m^2}\)

Điền số thích hợp vào ô trống:
\(4000c{m^2} =\)
\( \,d{m^2}\)

\(1890{m^2}\) được đọc là:
A. Một nghìn tám trăm chín chục mét vuông.
B. Một nghìn tám chín mươi mét vuông.
C. Một nghìn tám trăm chín không mét vuông.
D. Một nghìn tám trăm chín mươi mét vuông

Điền số thích hợp vào ô trống:
Ba mươi hai nghìn chín trăm sáu mươi lăm đề-xi-mét vuông viết là
\(\,\,d{m^2}\).

\(7{m^2}\,4d{m^2} = \,...\,d{m^2}\).
Số thích hợp điền vào chỗ chấm là:
A. \(74\)
B. \(704\)
C. \(740\)
D. \(7004\)

Điền dấu (\(>; <; =\)) thích hợp vào ô trống:
\(2002c{m^2}\,\,\)
\(\,\,20d{m^2}\,20c{m^2}\)
Cho hình chữ nhật có kích thước như hình vẽ dưới đây:
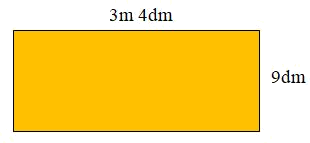
Diện tích hình chữ nhật đó là:
A. \(306d{m^2}\)
B. \(316d{m^2}\)
C. \(306{m^2}\)
D. \(316{m^2}\)

Cho hình vuông ABCD có $AB = 6m$. Hỏi diện tích hình vuông ABCD bằng bao nhiêu đề-xi-mét vuông?
A. \(36d{m^2}\)
B. \(360d{m^2}\)
C. \(3600d{m^2}\)
D. \(36000d{m^2}\)
Lời giải và đáp án

Đề-xi-mét vuông được kí hiệu là:
A. \(c{m^2}\)
B. \(d{m^2}\)
C. \({m^2}\)
D. \(m{m^2}\)
B. \(d{m^2}\)
Đề-xi-mét vuông được kí hiệu là \(d{m^2}\).

Điền số thích hợp vào ô trống:
\(3 d{m^2} =\)
\(\,c{m^2}\)
\(3 d{m^2} =\)
300\(\,c{m^2}\)
Dựa vào tính chất: \(1d{m^2} = 100c{m^2}\)
Ta có: \(1d{m^2} = 100c{m^2}\)
Nên \(3d{m^2} = 300\,c{m^2}\)Vậy đáp án đúng điền vào ô trống là \(300\).

Điền số thích hợp vào ô trống:
\(12{m^2} =\)
\(d{m^2}\)
\(12{m^2} =\)
1200\(d{m^2}\)
Dựa vào tính chất: \(1{m^2} = 100d{m^2}\).
Ta có: \(1{m^2} = 100d{m^2}\)
Nên \(12{m^2} = 1200d{m^2}\)Vậy đáp án đúng điền vào ô trống là \(1200\).

Điền số thích hợp vào ô trống:
\(4000c{m^2} =\)
\( \,d{m^2}\)
\(4000c{m^2} =\)
40\( \,d{m^2}\)
Dựa vào tính chất: \(1d{m^2} = 100c{m^2}\).
Ta có: \(1d{m^2} = 100c{m^2}\)
Nhẩm: \(4000:100 = 40\)
Do đó \(4000c{m^2} = 40d{m^2}\)Vậy đáp án đúng điền vào ô trống là \(40\).

\(1890{m^2}\) được đọc là:
A. Một nghìn tám trăm chín chục mét vuông.
B. Một nghìn tám chín mươi mét vuông.
C. Một nghìn tám trăm chín không mét vuông.
D. Một nghìn tám trăm chín mươi mét vuông
D. Một nghìn tám trăm chín mươi mét vuông
Đọc số đo diện tích trước rồi đọc tên đơn vị đo diện tích sau.
\(1890{m^2}\) đọc là một nghìn tám trăm chín mươi mét vuông.

Điền số thích hợp vào ô trống:
Ba mươi hai nghìn chín trăm sáu mươi lăm đề-xi-mét vuông viết là
\(\,\,d{m^2}\).
Ba mươi hai nghìn chín trăm sáu mươi lăm đề-xi-mét vuông viết là
32965\(\,\,d{m^2}\).
Viết số đo diện tích trước rồi viết tên đơn vị đo diện tích sau.
Ba mươi hai nghìn chín trăm sáu mươi lăm đề-xi-mét vuông viết là \(32965\,\,d{m^2}\).
Vậy số thích hợp điền vào ô trống là \(32965\).

\(7{m^2}\,4d{m^2} = \,...\,d{m^2}\).
Số thích hợp điền vào chỗ chấm là:
A. \(74\)
B. \(704\)
C. \(740\)
D. \(7004\)
B. \(704\)
Áp dụng tính chất: \(1{m^2} = 100d{m^2}\) để đổi \(7{m^2}\) sang đơn vị \(d{m^2}\), sau đó cộng thêm với \(4d{m^2}\).
Ta có \(1{m^2} = 100d{m^2}\) nên \(7{m^2} = 700d{m^2}\).
\(7{m^2}\,4d{m^2} = 7{m^2} + 4d{m^2} = 700d{m^2} + 4d{m^2} = 704d{m^2}\)
Vậy: \(7{m^2}\,4d{m^2} \,= \,704d{m^2}\).

Điền dấu (\(>; <; =\)) thích hợp vào ô trống:
\(2002c{m^2}\,\,\)
\(\,\,20d{m^2}\,20c{m^2}\)
\(2002c{m^2}\,\,\)
<\(\,\,20d{m^2}\,20c{m^2}\)
Đưa về cùng một đơn vị đo rồi so sánh kết quả với nhau.
Ta có: \(20d{m^2}\,20c{m^2} = \,20d{m^2} + 20c{m^2} = 2000c{m^2} + 20c{m^2} = 2020c{m^2}\)
Mà \(2002c{m^2} < 2020c{m^2}\)
Do đó \(2002c{m^2}\,\, < \,\,20d{m^2}\,20c{m^2}\)
Vậy đáp án đúng điền vào ô trống là \( < \).
Cho hình chữ nhật có kích thước như hình vẽ dưới đây:
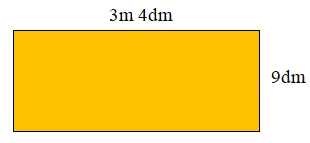
Diện tích hình chữ nhật đó là:
A. \(306d{m^2}\)
B. \(316d{m^2}\)
C. \(306{m^2}\)
D. \(316{m^2}\)
A. \(306d{m^2}\)
- Đổi \(3m\,\,4dm\) sang đơn vị đo là \(dm\).
- Tính diện tích hình chữ nhật theo công thức:
Diện tích = chiều dài × chiều rộng
Đổi $3m\,\,\,4dm{\rm{ }}\; = {\rm{ }}\;34dm$
Diện tích hình chữ nhật trên là:
$34 \times 9 = 306\,\,(d{m^2})$
Đáp số: \(306d{m^2}\).

Cho hình vuông ABCD có $AB = 6m$. Hỏi diện tích hình vuông ABCD bằng bao nhiêu đề-xi-mét vuông?
A. \(36d{m^2}\)
B. \(360d{m^2}\)
C. \(3600d{m^2}\)
D. \(36000d{m^2}\)
C. \(3600d{m^2}\)
- Đổi độ dài cạnh sang đơn vị đề-xi-mét vuông rồi tính diện tích hình vuông, hoặc tính diện tích với đơn vị đo mét vuông sau đó đổi sang đơn vị đề-xi-mét vuông.
- Tính diện tích theo công thức: diện tích = cạnh × cạnh.
Đổi: \(6m = 60dm\)
Diện tích hình vuông ABCD là:
\(60 \times 60 = 3600\,\,(d{m^2})\)
Đáp số: \(3600d{m^2}\).

Đề-xi-mét vuông được kí hiệu là:
A. \(c{m^2}\)
B. \(d{m^2}\)
C. \({m^2}\)
D. \(m{m^2}\)

Điền số thích hợp vào ô trống:
\(3 d{m^2} =\)
\(\,c{m^2}\)

Điền số thích hợp vào ô trống:
\(12{m^2} =\)
\(d{m^2}\)

Điền số thích hợp vào ô trống:
\(4000c{m^2} =\)
\( \,d{m^2}\)

\(1890{m^2}\) được đọc là:
A. Một nghìn tám trăm chín chục mét vuông.
B. Một nghìn tám chín mươi mét vuông.
C. Một nghìn tám trăm chín không mét vuông.
D. Một nghìn tám trăm chín mươi mét vuông

Điền số thích hợp vào ô trống:
Ba mươi hai nghìn chín trăm sáu mươi lăm đề-xi-mét vuông viết là
\(\,\,d{m^2}\).

\(7{m^2}\,4d{m^2} = \,...\,d{m^2}\).
Số thích hợp điền vào chỗ chấm là:
A. \(74\)
B. \(704\)
C. \(740\)
D. \(7004\)

Điền dấu (\(>; <; =\)) thích hợp vào ô trống:
\(2002c{m^2}\,\,\)
\(\,\,20d{m^2}\,20c{m^2}\)
Cho hình chữ nhật có kích thước như hình vẽ dưới đây:

Diện tích hình chữ nhật đó là:
A. \(306d{m^2}\)
B. \(316d{m^2}\)
C. \(306{m^2}\)
D. \(316{m^2}\)

Cho hình vuông ABCD có $AB = 6m$. Hỏi diện tích hình vuông ABCD bằng bao nhiêu đề-xi-mét vuông?
A. \(36d{m^2}\)
B. \(360d{m^2}\)
C. \(3600d{m^2}\)
D. \(36000d{m^2}\)

Đề-xi-mét vuông được kí hiệu là:
A. \(c{m^2}\)
B. \(d{m^2}\)
C. \({m^2}\)
D. \(m{m^2}\)
B. \(d{m^2}\)
Đề-xi-mét vuông được kí hiệu là \(d{m^2}\).

Điền số thích hợp vào ô trống:
\(3 d{m^2} =\)
\(\,c{m^2}\)
\(3 d{m^2} =\)
300\(\,c{m^2}\)
Dựa vào tính chất: \(1d{m^2} = 100c{m^2}\)
Ta có: \(1d{m^2} = 100c{m^2}\)
Nên \(3d{m^2} = 300\,c{m^2}\)Vậy đáp án đúng điền vào ô trống là \(300\).

Điền số thích hợp vào ô trống:
\(12{m^2} =\)
\(d{m^2}\)
\(12{m^2} =\)
1200\(d{m^2}\)
Dựa vào tính chất: \(1{m^2} = 100d{m^2}\).
Ta có: \(1{m^2} = 100d{m^2}\)
Nên \(12{m^2} = 1200d{m^2}\)Vậy đáp án đúng điền vào ô trống là \(1200\).

Điền số thích hợp vào ô trống:
\(4000c{m^2} =\)
\( \,d{m^2}\)
\(4000c{m^2} =\)
40\( \,d{m^2}\)
Dựa vào tính chất: \(1d{m^2} = 100c{m^2}\).
Ta có: \(1d{m^2} = 100c{m^2}\)
Nhẩm: \(4000:100 = 40\)
Do đó \(4000c{m^2} = 40d{m^2}\)Vậy đáp án đúng điền vào ô trống là \(40\).

\(1890{m^2}\) được đọc là:
A. Một nghìn tám trăm chín chục mét vuông.
B. Một nghìn tám chín mươi mét vuông.
C. Một nghìn tám trăm chín không mét vuông.
D. Một nghìn tám trăm chín mươi mét vuông
D. Một nghìn tám trăm chín mươi mét vuông
Đọc số đo diện tích trước rồi đọc tên đơn vị đo diện tích sau.
\(1890{m^2}\) đọc là một nghìn tám trăm chín mươi mét vuông.

Điền số thích hợp vào ô trống:
Ba mươi hai nghìn chín trăm sáu mươi lăm đề-xi-mét vuông viết là
\(\,\,d{m^2}\).
Ba mươi hai nghìn chín trăm sáu mươi lăm đề-xi-mét vuông viết là
32965\(\,\,d{m^2}\).
Viết số đo diện tích trước rồi viết tên đơn vị đo diện tích sau.
Ba mươi hai nghìn chín trăm sáu mươi lăm đề-xi-mét vuông viết là \(32965\,\,d{m^2}\).
Vậy số thích hợp điền vào ô trống là \(32965\).

\(7{m^2}\,4d{m^2} = \,...\,d{m^2}\).
Số thích hợp điền vào chỗ chấm là:
A. \(74\)
B. \(704\)
C. \(740\)
D. \(7004\)
B. \(704\)
Áp dụng tính chất: \(1{m^2} = 100d{m^2}\) để đổi \(7{m^2}\) sang đơn vị \(d{m^2}\), sau đó cộng thêm với \(4d{m^2}\).
Ta có \(1{m^2} = 100d{m^2}\) nên \(7{m^2} = 700d{m^2}\).
\(7{m^2}\,4d{m^2} = 7{m^2} + 4d{m^2} = 700d{m^2} + 4d{m^2} = 704d{m^2}\)
Vậy: \(7{m^2}\,4d{m^2} \,= \,704d{m^2}\).

Điền dấu (\(>; <; =\)) thích hợp vào ô trống:
\(2002c{m^2}\,\,\)
\(\,\,20d{m^2}\,20c{m^2}\)
\(2002c{m^2}\,\,\)
<\(\,\,20d{m^2}\,20c{m^2}\)
Đưa về cùng một đơn vị đo rồi so sánh kết quả với nhau.
Ta có: \(20d{m^2}\,20c{m^2} = \,20d{m^2} + 20c{m^2} = 2000c{m^2} + 20c{m^2} = 2020c{m^2}\)
Mà \(2002c{m^2} < 2020c{m^2}\)
Do đó \(2002c{m^2}\,\, < \,\,20d{m^2}\,20c{m^2}\)
Vậy đáp án đúng điền vào ô trống là \( < \).
Cho hình chữ nhật có kích thước như hình vẽ dưới đây:

Diện tích hình chữ nhật đó là:
A. \(306d{m^2}\)
B. \(316d{m^2}\)
C. \(306{m^2}\)
D. \(316{m^2}\)
A. \(306d{m^2}\)
- Đổi \(3m\,\,4dm\) sang đơn vị đo là \(dm\).
- Tính diện tích hình chữ nhật theo công thức:
Diện tích = chiều dài × chiều rộng
Đổi $3m\,\,\,4dm{\rm{ }}\; = {\rm{ }}\;34dm$
Diện tích hình chữ nhật trên là:
$34 \times 9 = 306\,\,(d{m^2})$
Đáp số: \(306d{m^2}\).

Cho hình vuông ABCD có $AB = 6m$. Hỏi diện tích hình vuông ABCD bằng bao nhiêu đề-xi-mét vuông?
A. \(36d{m^2}\)
B. \(360d{m^2}\)
C. \(3600d{m^2}\)
D. \(36000d{m^2}\)
C. \(3600d{m^2}\)
- Đổi độ dài cạnh sang đơn vị đề-xi-mét vuông rồi tính diện tích hình vuông, hoặc tính diện tích với đơn vị đo mét vuông sau đó đổi sang đơn vị đề-xi-mét vuông.
- Tính diện tích theo công thức: diện tích = cạnh × cạnh.
Đổi: \(6m = 60dm\)
Diện tích hình vuông ABCD là:
\(60 \times 60 = 3600\,\,(d{m^2})\)
Đáp số: \(3600d{m^2}\).
Bài 68 Toán 4 Cánh diều tập trung vào việc làm quen với đơn vị đo diện tích là đề-xi-mét vuông (dm2). Học sinh cần nắm vững mối quan hệ giữa dm2 và cm2 (1 dm2 = 100 cm2) để giải quyết các bài toán thực tế. Bài học này cũng giúp các em hiểu rõ hơn về cách tính diện tích của các hình vuông và hình chữ nhật khi kích thước đã cho.
Các bài tập dạng này yêu cầu học sinh đổi đổi từ cm2 sang dm2 hoặc ngược lại. Lưu ý sử dụng mối quan hệ 1 dm2 = 100 cm2 để thực hiện phép đổi.
Ví dụ: Đổi 300 cm2 ra dm2. Giải: 300 cm2 = 300 : 100 dm2 = 3 dm2
Để tính diện tích hình vuông, học sinh cần biết độ dài một cạnh của hình vuông. Sau đó, áp dụng công thức S = a x a để tính diện tích.
Ví dụ: Một hình vuông có cạnh dài 5 dm. Tính diện tích hình vuông đó. Giải: Diện tích hình vuông là: 5 x 5 = 25 dm2
Để tính diện tích hình chữ nhật, học sinh cần biết chiều dài và chiều rộng của hình chữ nhật. Sau đó, áp dụng công thức S = a x b để tính diện tích.
Ví dụ: Một hình chữ nhật có chiều dài 8 dm và chiều rộng 4 dm. Tính diện tích hình chữ nhật đó. Giải: Diện tích hình chữ nhật là: 8 x 4 = 32 dm2
Các bài toán ứng dụng yêu cầu học sinh vận dụng kiến thức về diện tích để giải quyết các tình huống thực tế. Ví dụ: Tính diện tích một mảnh đất hình chữ nhật, tính số lượng gạch cần để lát một căn phòng, v.v.
Hy vọng bài viết này đã cung cấp cho các em những kiến thức cần thiết để giải quyết các bài tập về Trắc nghiệm Bài 68: Đề-xi-mét vuông Toán 4 Cánh diều. Chúc các em học tập tốt và đạt kết quả cao!