Chào mừng các em học sinh lớp 4 đến với bài trắc nghiệm Bài 62: So sánh hai phân số khác mẫu số trong chương trình Toán 4 Cánh diều. Bài tập này được thiết kế để giúp các em củng cố kiến thức và kỹ năng so sánh phân số một cách hiệu quả.
Tại giaitoan.edu.vn, chúng tôi cung cấp một bộ câu hỏi trắc nghiệm đa dạng, bao gồm nhiều dạng bài tập khác nhau, giúp các em làm quen với các phương pháp so sánh phân số khác nhau.

Chọn dấu thích hợp để điền vào chỗ chấm:
\(\dfrac{7}{8} \cdot \cdot \cdot \dfrac{3}{8}\)
A. \( > \)
B. \( < \)
C. \( = \)

Phân số nào dưới đây bé hơn phân số \(\dfrac{4}{9}\)?
A. \(\dfrac{7}{9}\)
B. \(\dfrac{8}{9}\)
C. \(\dfrac{3}{9}\)
D. \(\dfrac{5}{9}\)

Điền dấu (\(<;\,>;\,=\)) thích hợp vào ô trống:
\(\dfrac{7}{9}\,\,\)
\(\,\dfrac{{35}}{{45}}\)

Chọn dấu thích hợp để điền vào chỗ chấm:
\(\dfrac{3}{5} \cdot \cdot \cdot \dfrac{5}{6}\)
A. \( < \)
B. \( > \)
C. \( = \)

\(\dfrac{{13}}{{36}} \cdot \cdot \cdot \dfrac{{13}}{{25}}\)
Dấu thích hợp điền vào chỗ chấm là:
A. \( = \)
B. \( > \)
C. \( < \)

Hoa ăn \(\dfrac{5}{8}\) cái bánh, Lan ăn \(\dfrac{3}{5}\) cái bánh. Hỏi ai ăn nhiều bánh hơn?
A. Hoa
B. Lan
C. Hai bạn ăn bằng nhau

Hình nào dưới đây có phân số chỉ phần tô đậm bé hơn \(\dfrac{1}{3}\)?
A.
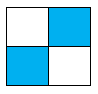
B.
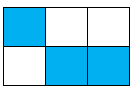
C.
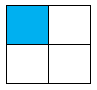
D.
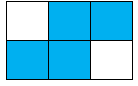

Rút gọn rồi so sánh hai phân số \(\dfrac{{120}}{{162}}\) và \(\dfrac{{108}}{{135}}\).
Vậy phân số lớn hơn là:
A. \(\dfrac{{120}}{{162}}\)
B. \(\dfrac{{108}}{{135}}\)

Chọn phân số bé hơn trong hai phân số sau:
A. \(\dfrac{2}{{87}}\)
B. \(\dfrac{3}{{131}}\)
Lời giải và đáp án

Chọn dấu thích hợp để điền vào chỗ chấm:
\(\dfrac{7}{8} \cdot \cdot \cdot \dfrac{3}{8}\)
A. \( > \)
B. \( < \)
C. \( = \)
A. \( > \)
Áp dụng quy tắc so sánh hai phân số có cùng mẫu số:
Trong hai phân số có cùng mẫu số:
+) Phân số nào có tử số bé hơn thì phân số đó bé hơn.
+) Phân số nào có tử số lớn hơn thì phân số đó lớn hơn.
+) Nếu tử số bằng nhau thì hai phân số đó bằng nhau.
Ta thấy hai phân số \(\dfrac{7}{8}\) và \(\dfrac{3}{8}\) đều có mẫu số là \(8\) và \(7 > 3\) nên \(\dfrac{7}{8} > \dfrac{3}{8}\).
Vậy dấu thích hợp điền vào chỗ chấm là \(>\).

Phân số nào dưới đây bé hơn phân số \(\dfrac{4}{9}\)?
A. \(\dfrac{7}{9}\)
B. \(\dfrac{8}{9}\)
C. \(\dfrac{3}{9}\)
D. \(\dfrac{5}{9}\)
C. \(\dfrac{3}{9}\)
Áp dụng quy tắc so sánh hai phân số có cùng mẫu số.
Ta thấy các phân số đã cho đều có mẫu số là \(9\) và \(3 < 4 < 7 < 8\) nên \(\dfrac{3}{9} < \dfrac{4}{9} < \dfrac{7}{9} < \dfrac{8}{9}\).
Vậy phân số bé hơn \(\dfrac{4}{9}\) là \(\dfrac{3}{9}\).

Điền dấu (\(<;\,>;\,=\)) thích hợp vào ô trống:
\(\dfrac{7}{9}\,\,\)
\(\,\dfrac{{35}}{{45}}\)
\(\dfrac{7}{9}\,\,\)
=\(\,\dfrac{{35}}{{45}}\)
Quy đồng mẫu số hai phân số, sau đó so sánh hai phân số sau khi quy đồng.
\(MSC = 45\).
Quy đồng mẫu số hai phân số ta có:
\(\dfrac{7}{9} = \dfrac{{7 \times 5}}{{9 \times 5}} = \dfrac{{35}}{{45}}\) Giữ nguyên phân số \(\dfrac{{35}}{{45}}\).
Ta thấy \(\dfrac{{35}}{{45}}\, = \,\dfrac{{35}}{{45}}\) nên \(\dfrac{7}{9}\, = \,\dfrac{{35}}{{45}}\)
Vậy dấu thích hợp điền vào ô trống là dấu \( = \).

Chọn dấu thích hợp để điền vào chỗ chấm:
\(\dfrac{3}{5} \cdot \cdot \cdot \dfrac{5}{6}\)
A. \( < \)
B. \( > \)
C. \( = \)
A. \( < \)
Quy đồng mẫu số hai phân số, sau đó so sánh hai phân số sau khi quy đồng.
\(MSC = 30\).
Quy đồng mẫu số hai phân số ta có:
\(\dfrac{3}{5} = \dfrac{{3 \times 6}}{{5 \times 6}} = \dfrac{{18}}{{30}};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{5}{6} = \dfrac{{5 \times 5}}{{6 \times 5}} = \dfrac{{25}}{{30}}\)
Mà \(\dfrac{{18}}{{30}} < \dfrac{{25}}{{30}}\) (vì \(18 < 25\)).
Vậy \(\dfrac{3}{5} < \dfrac{5}{6}\).

\(\dfrac{{13}}{{36}} \cdot \cdot \cdot \dfrac{{13}}{{25}}\)
Dấu thích hợp điền vào chỗ chấm là:
A. \( = \)
B. \( > \)
C. \( < \)
C. \( < \)
Dựa vào quy tắc so sánh hai phân số có cùng tử số:
Trong hai phân số có cùng tử số:
+) Phân số nào có mẫu số bé hơn thì phân số đó lớn hơn.
+) Phân số nào có mẫu số lớn hơn thì phân số đó bé hơn.
+) Nếu mẫu số bằng nhau thì hai phân số đó bằng nhau.
Ta thấy hai phân số \(\dfrac{{13}}{{36}}\) và \(\dfrac{{13}}{{25}}\) đều có tử số là \(13\) và \(36 > 25\) nên \(\dfrac{{13}}{{36}} < \dfrac{{13}}{{25}}\).
Vậy dấu thích hợp điền vào chỗ chấm là \(<\).

Hoa ăn \(\dfrac{5}{8}\) cái bánh, Lan ăn \(\dfrac{3}{5}\) cái bánh. Hỏi ai ăn nhiều bánh hơn?
A. Hoa
B. Lan
C. Hai bạn ăn bằng nhau
A. Hoa
Quy đồng mẫu số hai phân số chỉ số bánh hai bạn đã ăn, sau đó so sánh hai phân số sau khi quy đồng.
Ta sẽ so sánh hai phân số: \(\dfrac{5}{8}\) và \(\dfrac{3}{5}\).
$MSC = 40$
Quy đồng mẫu số hai phân số ta có:
\(\dfrac{5}{8} = \dfrac{{5 \times 5}}{{8 \times 5}} = \dfrac{{25}}{{40}}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{3}{5} = \dfrac{{3 \times 8}}{{5 \times 8}} = \dfrac{{24}}{{40}}\)
Mà \(\dfrac{{25}}{{40}} > \dfrac{{24}}{{40}}\) (vì \(25 > 24\) )
Do đó: \(\dfrac{5}{8} > \dfrac{3}{5}\)
Vậy Hoa ăn nhiều bánh hơn.

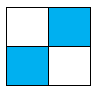
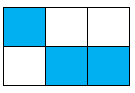
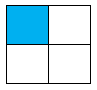
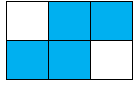
Hình nào dưới đây có phân số chỉ phần tô đậm bé hơn \(\dfrac{1}{3}\)?
A.
B.
C.
D.
C.
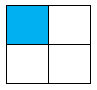
- Xác định phân số chỉ phần tô đậm của mỗi hình.
- Quy đồng tử số hoặc mẫu số hai phân số, sau đó so sánh hai phân số sau khi quy đồng.
Phân số chỉ phần tô đậm của hình A là \(\dfrac{2}{4} = \dfrac{1}{2}\).
Phân số chỉ phần tô đậm của hình B là \(\dfrac{3}{6} = \dfrac{1}{2}\).
Phân số chỉ phần tô đậm của hình C là \(\dfrac{1}{4}\).
Phân số chỉ phần tô đậm của hình D là \(\dfrac{4}{6} = \dfrac{2}{3}\).
Ta có: \(\dfrac{1}{2} > \dfrac{1}{3}\) (vì \(2 < 3\)) nên \(\dfrac{2}{4} > \dfrac{1}{3}\,\,\,;\,\,\,\,\,\dfrac{3}{6} > \dfrac{1}{3}\).
\(\dfrac{1}{4} < \dfrac{1}{3}\) (vì \(4 > 3\)) .
\(\dfrac{2}{3} > \dfrac{1}{3}\) (vì \(2 > 1\)) nên \(\dfrac{4}{6}\,\, > \dfrac{1}{3}\).
Do đó phân số bé hơn \(\dfrac{1}{3}\) là \(\dfrac{1}{4}\).
Vậy hình C có phân số chỉ phần tô đậm bé hơn \(\dfrac{1}{3}\).

Rút gọn rồi so sánh hai phân số \(\dfrac{{120}}{{162}}\) và \(\dfrac{{108}}{{135}}\).
Vậy phân số lớn hơn là:
A. \(\dfrac{{120}}{{162}}\)
B. \(\dfrac{{108}}{{135}}\)
B. \(\dfrac{{108}}{{135}}\)
- Rút gọn hai phân số đã cho thành phân số tối giản
- So sánh hai phân số mới. Nếu hai phân số mới có cùng tử số hoặc mẫu số thì ta áp dụng quy tắc để so sánh luôn, ngược lại thì ta quy đồng tử số hoặc mẫu số để so sánh.
Rút gọn hai phân số đã cho ta có:
$\begin{array}{l}\dfrac{{120}}{{162}} = \dfrac{{120:2}}{{162:2}} = \dfrac{{60}}{{81}} = \dfrac{{60:3}}{{81:3}} = \dfrac{{20}}{{27}};\,\,\,\,\,\,\,\,\,\,\,\,\,\\\dfrac{{108}}{{135}} = \dfrac{{108:9}}{{135:9}} = \dfrac{{12}}{{15}} = \dfrac{{12:3}}{{15:3}} = \dfrac{4}{5} \cdot \end{array}$
Ta sẽ so sánh hai phân số \(\dfrac{{20}}{{27}}\) và \(\dfrac{4}{5}\) bằng cách quy đồng tử số.
Chọn tử số chung là \(20\).
Giữ nguyên phân số \(\dfrac{{20}}{{27}}\); \(\dfrac{4}{5} = \dfrac{{4 \times 5}}{{5 \times 5}} = \dfrac{{20}}{{25}}\)
Mà \(\dfrac{{20}}{{27}} < \dfrac{{20}}{{25}}\) (vì \(27 > 25\)).
Do đó \(\dfrac{{20}}{{27}} < \dfrac{4}{5}\) , hay \(\dfrac{{120}}{{162}} < \dfrac{{108}}{{135}}\)
Vậy phân số lớn hơn là \(\dfrac{{108}}{{135}}\).

Chọn phân số bé hơn trong hai phân số sau:
A. \(\dfrac{2}{{87}}\)
B. \(\dfrac{3}{{131}}\)
B. \(\dfrac{3}{{131}}\)
Quy đồng tử số hai phân số, sau đó so sánh hai phân số sau khi quy đồng.
TSC = \(6\).
Quy đồng tử số hai phân số ta có:
\(\dfrac{2}{{87}} = \dfrac{{2 \times 3}}{{87 \times 3}} = \dfrac{6}{{261}}\);
\(\dfrac{3}{{131}} = \dfrac{{3 \times 2}}{{131 \times 2}} = \dfrac{6}{{262}}\)
Mà \(\dfrac{6}{{261}} > \dfrac{6}{{262}}\) (vì \(261 < 262\))
Do đó \(\dfrac{2}{{87}} > \dfrac{3}{{131}}\)
Vậy phân số bé hơn là \(\dfrac{3}{{131}}\).

Chọn dấu thích hợp để điền vào chỗ chấm:
\(\dfrac{7}{8} \cdot \cdot \cdot \dfrac{3}{8}\)
A. \( > \)
B. \( < \)
C. \( = \)

Phân số nào dưới đây bé hơn phân số \(\dfrac{4}{9}\)?
A. \(\dfrac{7}{9}\)
B. \(\dfrac{8}{9}\)
C. \(\dfrac{3}{9}\)
D. \(\dfrac{5}{9}\)

Điền dấu (\(<;\,>;\,=\)) thích hợp vào ô trống:
\(\dfrac{7}{9}\,\,\)
\(\,\dfrac{{35}}{{45}}\)

Chọn dấu thích hợp để điền vào chỗ chấm:
\(\dfrac{3}{5} \cdot \cdot \cdot \dfrac{5}{6}\)
A. \( < \)
B. \( > \)
C. \( = \)

\(\dfrac{{13}}{{36}} \cdot \cdot \cdot \dfrac{{13}}{{25}}\)
Dấu thích hợp điền vào chỗ chấm là:
A. \( = \)
B. \( > \)
C. \( < \)

Hoa ăn \(\dfrac{5}{8}\) cái bánh, Lan ăn \(\dfrac{3}{5}\) cái bánh. Hỏi ai ăn nhiều bánh hơn?
A. Hoa
B. Lan
C. Hai bạn ăn bằng nhau

Hình nào dưới đây có phân số chỉ phần tô đậm bé hơn \(\dfrac{1}{3}\)?
A.

B.

C.

D.


Rút gọn rồi so sánh hai phân số \(\dfrac{{120}}{{162}}\) và \(\dfrac{{108}}{{135}}\).
Vậy phân số lớn hơn là:
A. \(\dfrac{{120}}{{162}}\)
B. \(\dfrac{{108}}{{135}}\)

Chọn phân số bé hơn trong hai phân số sau:
A. \(\dfrac{2}{{87}}\)
B. \(\dfrac{3}{{131}}\)

Chọn dấu thích hợp để điền vào chỗ chấm:
\(\dfrac{7}{8} \cdot \cdot \cdot \dfrac{3}{8}\)
A. \( > \)
B. \( < \)
C. \( = \)
A. \( > \)
Áp dụng quy tắc so sánh hai phân số có cùng mẫu số:
Trong hai phân số có cùng mẫu số:
+) Phân số nào có tử số bé hơn thì phân số đó bé hơn.
+) Phân số nào có tử số lớn hơn thì phân số đó lớn hơn.
+) Nếu tử số bằng nhau thì hai phân số đó bằng nhau.
Ta thấy hai phân số \(\dfrac{7}{8}\) và \(\dfrac{3}{8}\) đều có mẫu số là \(8\) và \(7 > 3\) nên \(\dfrac{7}{8} > \dfrac{3}{8}\).
Vậy dấu thích hợp điền vào chỗ chấm là \(>\).

Phân số nào dưới đây bé hơn phân số \(\dfrac{4}{9}\)?
A. \(\dfrac{7}{9}\)
B. \(\dfrac{8}{9}\)
C. \(\dfrac{3}{9}\)
D. \(\dfrac{5}{9}\)
C. \(\dfrac{3}{9}\)
Áp dụng quy tắc so sánh hai phân số có cùng mẫu số.
Ta thấy các phân số đã cho đều có mẫu số là \(9\) và \(3 < 4 < 7 < 8\) nên \(\dfrac{3}{9} < \dfrac{4}{9} < \dfrac{7}{9} < \dfrac{8}{9}\).
Vậy phân số bé hơn \(\dfrac{4}{9}\) là \(\dfrac{3}{9}\).

Điền dấu (\(<;\,>;\,=\)) thích hợp vào ô trống:
\(\dfrac{7}{9}\,\,\)
\(\,\dfrac{{35}}{{45}}\)
\(\dfrac{7}{9}\,\,\)
=\(\,\dfrac{{35}}{{45}}\)
Quy đồng mẫu số hai phân số, sau đó so sánh hai phân số sau khi quy đồng.
\(MSC = 45\).
Quy đồng mẫu số hai phân số ta có:
\(\dfrac{7}{9} = \dfrac{{7 \times 5}}{{9 \times 5}} = \dfrac{{35}}{{45}}\) Giữ nguyên phân số \(\dfrac{{35}}{{45}}\).
Ta thấy \(\dfrac{{35}}{{45}}\, = \,\dfrac{{35}}{{45}}\) nên \(\dfrac{7}{9}\, = \,\dfrac{{35}}{{45}}\)
Vậy dấu thích hợp điền vào ô trống là dấu \( = \).

Chọn dấu thích hợp để điền vào chỗ chấm:
\(\dfrac{3}{5} \cdot \cdot \cdot \dfrac{5}{6}\)
A. \( < \)
B. \( > \)
C. \( = \)
A. \( < \)
Quy đồng mẫu số hai phân số, sau đó so sánh hai phân số sau khi quy đồng.
\(MSC = 30\).
Quy đồng mẫu số hai phân số ta có:
\(\dfrac{3}{5} = \dfrac{{3 \times 6}}{{5 \times 6}} = \dfrac{{18}}{{30}};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{5}{6} = \dfrac{{5 \times 5}}{{6 \times 5}} = \dfrac{{25}}{{30}}\)
Mà \(\dfrac{{18}}{{30}} < \dfrac{{25}}{{30}}\) (vì \(18 < 25\)).
Vậy \(\dfrac{3}{5} < \dfrac{5}{6}\).

\(\dfrac{{13}}{{36}} \cdot \cdot \cdot \dfrac{{13}}{{25}}\)
Dấu thích hợp điền vào chỗ chấm là:
A. \( = \)
B. \( > \)
C. \( < \)
C. \( < \)
Dựa vào quy tắc so sánh hai phân số có cùng tử số:
Trong hai phân số có cùng tử số:
+) Phân số nào có mẫu số bé hơn thì phân số đó lớn hơn.
+) Phân số nào có mẫu số lớn hơn thì phân số đó bé hơn.
+) Nếu mẫu số bằng nhau thì hai phân số đó bằng nhau.
Ta thấy hai phân số \(\dfrac{{13}}{{36}}\) và \(\dfrac{{13}}{{25}}\) đều có tử số là \(13\) và \(36 > 25\) nên \(\dfrac{{13}}{{36}} < \dfrac{{13}}{{25}}\).
Vậy dấu thích hợp điền vào chỗ chấm là \(<\).

Hoa ăn \(\dfrac{5}{8}\) cái bánh, Lan ăn \(\dfrac{3}{5}\) cái bánh. Hỏi ai ăn nhiều bánh hơn?
A. Hoa
B. Lan
C. Hai bạn ăn bằng nhau
A. Hoa
Quy đồng mẫu số hai phân số chỉ số bánh hai bạn đã ăn, sau đó so sánh hai phân số sau khi quy đồng.
Ta sẽ so sánh hai phân số: \(\dfrac{5}{8}\) và \(\dfrac{3}{5}\).
$MSC = 40$
Quy đồng mẫu số hai phân số ta có:
\(\dfrac{5}{8} = \dfrac{{5 \times 5}}{{8 \times 5}} = \dfrac{{25}}{{40}}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{3}{5} = \dfrac{{3 \times 8}}{{5 \times 8}} = \dfrac{{24}}{{40}}\)
Mà \(\dfrac{{25}}{{40}} > \dfrac{{24}}{{40}}\) (vì \(25 > 24\) )
Do đó: \(\dfrac{5}{8} > \dfrac{3}{5}\)
Vậy Hoa ăn nhiều bánh hơn.

Hình nào dưới đây có phân số chỉ phần tô đậm bé hơn \(\dfrac{1}{3}\)?
A.

B.

C.

D.

C.

- Xác định phân số chỉ phần tô đậm của mỗi hình.
- Quy đồng tử số hoặc mẫu số hai phân số, sau đó so sánh hai phân số sau khi quy đồng.
Phân số chỉ phần tô đậm của hình A là \(\dfrac{2}{4} = \dfrac{1}{2}\).
Phân số chỉ phần tô đậm của hình B là \(\dfrac{3}{6} = \dfrac{1}{2}\).
Phân số chỉ phần tô đậm của hình C là \(\dfrac{1}{4}\).
Phân số chỉ phần tô đậm của hình D là \(\dfrac{4}{6} = \dfrac{2}{3}\).
Ta có: \(\dfrac{1}{2} > \dfrac{1}{3}\) (vì \(2 < 3\)) nên \(\dfrac{2}{4} > \dfrac{1}{3}\,\,\,;\,\,\,\,\,\dfrac{3}{6} > \dfrac{1}{3}\).
\(\dfrac{1}{4} < \dfrac{1}{3}\) (vì \(4 > 3\)) .
\(\dfrac{2}{3} > \dfrac{1}{3}\) (vì \(2 > 1\)) nên \(\dfrac{4}{6}\,\, > \dfrac{1}{3}\).
Do đó phân số bé hơn \(\dfrac{1}{3}\) là \(\dfrac{1}{4}\).
Vậy hình C có phân số chỉ phần tô đậm bé hơn \(\dfrac{1}{3}\).

Rút gọn rồi so sánh hai phân số \(\dfrac{{120}}{{162}}\) và \(\dfrac{{108}}{{135}}\).
Vậy phân số lớn hơn là:
A. \(\dfrac{{120}}{{162}}\)
B. \(\dfrac{{108}}{{135}}\)
B. \(\dfrac{{108}}{{135}}\)
- Rút gọn hai phân số đã cho thành phân số tối giản
- So sánh hai phân số mới. Nếu hai phân số mới có cùng tử số hoặc mẫu số thì ta áp dụng quy tắc để so sánh luôn, ngược lại thì ta quy đồng tử số hoặc mẫu số để so sánh.
Rút gọn hai phân số đã cho ta có:
$\begin{array}{l}\dfrac{{120}}{{162}} = \dfrac{{120:2}}{{162:2}} = \dfrac{{60}}{{81}} = \dfrac{{60:3}}{{81:3}} = \dfrac{{20}}{{27}};\,\,\,\,\,\,\,\,\,\,\,\,\,\\\dfrac{{108}}{{135}} = \dfrac{{108:9}}{{135:9}} = \dfrac{{12}}{{15}} = \dfrac{{12:3}}{{15:3}} = \dfrac{4}{5} \cdot \end{array}$
Ta sẽ so sánh hai phân số \(\dfrac{{20}}{{27}}\) và \(\dfrac{4}{5}\) bằng cách quy đồng tử số.
Chọn tử số chung là \(20\).
Giữ nguyên phân số \(\dfrac{{20}}{{27}}\); \(\dfrac{4}{5} = \dfrac{{4 \times 5}}{{5 \times 5}} = \dfrac{{20}}{{25}}\)
Mà \(\dfrac{{20}}{{27}} < \dfrac{{20}}{{25}}\) (vì \(27 > 25\)).
Do đó \(\dfrac{{20}}{{27}} < \dfrac{4}{5}\) , hay \(\dfrac{{120}}{{162}} < \dfrac{{108}}{{135}}\)
Vậy phân số lớn hơn là \(\dfrac{{108}}{{135}}\).

Chọn phân số bé hơn trong hai phân số sau:
A. \(\dfrac{2}{{87}}\)
B. \(\dfrac{3}{{131}}\)
B. \(\dfrac{3}{{131}}\)
Quy đồng tử số hai phân số, sau đó so sánh hai phân số sau khi quy đồng.
TSC = \(6\).
Quy đồng tử số hai phân số ta có:
\(\dfrac{2}{{87}} = \dfrac{{2 \times 3}}{{87 \times 3}} = \dfrac{6}{{261}}\);
\(\dfrac{3}{{131}} = \dfrac{{3 \times 2}}{{131 \times 2}} = \dfrac{6}{{262}}\)
Mà \(\dfrac{6}{{261}} > \dfrac{6}{{262}}\) (vì \(261 < 262\))
Do đó \(\dfrac{2}{{87}} > \dfrac{3}{{131}}\)
Vậy phân số bé hơn là \(\dfrac{3}{{131}}\).
Bài 62 trong chương trình Toán 4 Cánh diều tập trung vào việc so sánh hai phân số có mẫu số khác nhau. Đây là một kỹ năng quan trọng trong toán học, giúp học sinh hiểu rõ hơn về giá trị của phân số và ứng dụng trong các bài toán thực tế.
Để so sánh hai phân số có mẫu số khác nhau, chúng ta cần thực hiện các bước sau:
Có nhiều phương pháp để quy đồng mẫu số, bao gồm:
Ví dụ 1: So sánh hai phân số 2/3 và 3/4
Ví dụ 2: So sánh hai phân số 5/6 và 7/9
Dưới đây là một số câu hỏi trắc nghiệm để các em luyện tập:
Chúc các em học tốt và đạt kết quả cao trong các bài kiểm tra Toán 4!
| Phân số 1 | Phân số 2 | Kết quả so sánh |
|---|---|---|
| 1/4 | 1/3 | 1/4 < 1/3 |
| 2/5 | 3/7 | 2/5 > 3/7 |