Bài tập trắc nghiệm này được thiết kế để giúp học sinh lớp 4 ôn luyện và củng cố kiến thức về cách so sánh hai phân số có cùng mẫu số theo chương trình Cánh diều.
Với hình thức trắc nghiệm, học sinh có thể tự đánh giá năng lực của mình một cách nhanh chóng và hiệu quả.
Giaitoan.edu.vn cung cấp đầy đủ các dạng bài tập, đáp án và lời giải chi tiết để hỗ trợ quá trình học tập của các em.

Chọn dấu thích hợp để điền vào chỗ chấm:
\(\dfrac{7}{8} \cdot \cdot \cdot \dfrac{3}{8}\)
A. \( > \)
B. \( < \)
C. \( = \)

Phân số nào dưới đây bé hơn phân số \(\dfrac{4}{9}\)?
A. \(\dfrac{7}{9}\)
B. \(\dfrac{8}{9}\)
C. \(\dfrac{3}{9}\)
D. \(\dfrac{5}{9}\)

Điền dấu (\(<;\,>;\,=\)) thích hợp vào ô trống:
\(\dfrac{7}{9}\,\,\)
\(\,\dfrac{{35}}{{45}}\)

Chọn dấu thích hợp để điền vào chỗ chấm:
\(\dfrac{3}{5} \cdot \cdot \cdot \dfrac{5}{6}\)
A. \( < \)
B. \( > \)
C. \( = \)

\(\dfrac{{13}}{{36}} \cdot \cdot \cdot \dfrac{{13}}{{25}}\)
Dấu thích hợp điền vào chỗ chấm là:
A. \( = \)
B. \( > \)
C. \( < \)

Hoa ăn \(\dfrac{5}{8}\) cái bánh, Lan ăn \(\dfrac{3}{5}\) cái bánh. Hỏi ai ăn nhiều bánh hơn?
A. Hoa
B. Lan
C. Hai bạn ăn bằng nhau

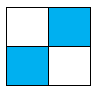
Hình nào dưới đây có phân số chỉ phần tô đậm bé hơn \(\dfrac{1}{3}\)?
A.
B.
C.
D.

Rút gọn rồi so sánh hai phân số \(\dfrac{{120}}{{162}}\) và \(\dfrac{{108}}{{135}}\).
Vậy phân số lớn hơn là:
A. \(\dfrac{{120}}{{162}}\)
B. \(\dfrac{{108}}{{135}}\)

Chọn phân số bé hơn trong hai phân số sau:
A. \(\dfrac{2}{{87}}\)
B. \(\dfrac{3}{{131}}\)
Lời giải và đáp án

Chọn dấu thích hợp để điền vào chỗ chấm:
\(\dfrac{7}{8} \cdot \cdot \cdot \dfrac{3}{8}\)
A. \( > \)
B. \( < \)
C. \( = \)
A. \( > \)
Áp dụng quy tắc so sánh hai phân số có cùng mẫu số:
Trong hai phân số có cùng mẫu số:
+) Phân số nào có tử số bé hơn thì phân số đó bé hơn.
+) Phân số nào có tử số lớn hơn thì phân số đó lớn hơn.
+) Nếu tử số bằng nhau thì hai phân số đó bằng nhau.
Ta thấy hai phân số \(\dfrac{7}{8}\) và \(\dfrac{3}{8}\) đều có mẫu số là \(8\) và \(7 > 3\) nên \(\dfrac{7}{8} > \dfrac{3}{8}\).
Vậy dấu thích hợp điền vào chỗ chấm là \(>\).

Phân số nào dưới đây bé hơn phân số \(\dfrac{4}{9}\)?
A. \(\dfrac{7}{9}\)
B. \(\dfrac{8}{9}\)
C. \(\dfrac{3}{9}\)
D. \(\dfrac{5}{9}\)
C. \(\dfrac{3}{9}\)
Áp dụng quy tắc so sánh hai phân số có cùng mẫu số.
Ta thấy các phân số đã cho đều có mẫu số là \(9\) và \(3 < 4 < 7 < 8\) nên \(\dfrac{3}{9} < \dfrac{4}{9} < \dfrac{7}{9} < \dfrac{8}{9}\).
Vậy phân số bé hơn \(\dfrac{4}{9}\) là \(\dfrac{3}{9}\).

Điền dấu (\(<;\,>;\,=\)) thích hợp vào ô trống:
\(\dfrac{7}{9}\,\,\)
\(\,\dfrac{{35}}{{45}}\)
\(\dfrac{7}{9}\,\,\)
=\(\,\dfrac{{35}}{{45}}\)
Quy đồng mẫu số hai phân số, sau đó so sánh hai phân số sau khi quy đồng.
\(MSC = 45\).
Quy đồng mẫu số hai phân số ta có:
\(\dfrac{7}{9} = \dfrac{{7 \times 5}}{{9 \times 5}} = \dfrac{{35}}{{45}}\) Giữ nguyên phân số \(\dfrac{{35}}{{45}}\).
Ta thấy \(\dfrac{{35}}{{45}}\, = \,\dfrac{{35}}{{45}}\) nên \(\dfrac{7}{9}\, = \,\dfrac{{35}}{{45}}\)
Vậy dấu thích hợp điền vào ô trống là dấu \( = \).

Chọn dấu thích hợp để điền vào chỗ chấm:
\(\dfrac{3}{5} \cdot \cdot \cdot \dfrac{5}{6}\)
A. \( < \)
B. \( > \)
C. \( = \)
A. \( < \)
Quy đồng mẫu số hai phân số, sau đó so sánh hai phân số sau khi quy đồng.
\(MSC = 30\).
Quy đồng mẫu số hai phân số ta có:
\(\dfrac{3}{5} = \dfrac{{3 \times 6}}{{5 \times 6}} = \dfrac{{18}}{{30}};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{5}{6} = \dfrac{{5 \times 5}}{{6 \times 5}} = \dfrac{{25}}{{30}}\)
Mà \(\dfrac{{18}}{{30}} < \dfrac{{25}}{{30}}\) (vì \(18 < 25\)).
Vậy \(\dfrac{3}{5} < \dfrac{5}{6}\).

\(\dfrac{{13}}{{36}} \cdot \cdot \cdot \dfrac{{13}}{{25}}\)
Dấu thích hợp điền vào chỗ chấm là:
A. \( = \)
B. \( > \)
C. \( < \)
C. \( < \)
Dựa vào quy tắc so sánh hai phân số có cùng tử số:
Trong hai phân số có cùng tử số:
+) Phân số nào có mẫu số bé hơn thì phân số đó lớn hơn.
+) Phân số nào có mẫu số lớn hơn thì phân số đó bé hơn.
+) Nếu mẫu số bằng nhau thì hai phân số đó bằng nhau.
Ta thấy hai phân số \(\dfrac{{13}}{{36}}\) và \(\dfrac{{13}}{{25}}\) đều có tử số là \(13\) và \(36 > 25\) nên \(\dfrac{{13}}{{36}} < \dfrac{{13}}{{25}}\).
Vậy dấu thích hợp điền vào chỗ chấm là \(<\).

Hoa ăn \(\dfrac{5}{8}\) cái bánh, Lan ăn \(\dfrac{3}{5}\) cái bánh. Hỏi ai ăn nhiều bánh hơn?
A. Hoa
B. Lan
C. Hai bạn ăn bằng nhau
A. Hoa
Quy đồng mẫu số hai phân số chỉ số bánh hai bạn đã ăn, sau đó so sánh hai phân số sau khi quy đồng.
Ta sẽ so sánh hai phân số: \(\dfrac{5}{8}\) và \(\dfrac{3}{5}\).
$MSC = 40$
Quy đồng mẫu số hai phân số ta có:
\(\dfrac{5}{8} = \dfrac{{5 \times 5}}{{8 \times 5}} = \dfrac{{25}}{{40}}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{3}{5} = \dfrac{{3 \times 8}}{{5 \times 8}} = \dfrac{{24}}{{40}}\)
Mà \(\dfrac{{25}}{{40}} > \dfrac{{24}}{{40}}\) (vì \(25 > 24\) )
Do đó: \(\dfrac{5}{8} > \dfrac{3}{5}\)
Vậy Hoa ăn nhiều bánh hơn.

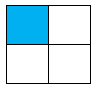
Hình nào dưới đây có phân số chỉ phần tô đậm bé hơn \(\dfrac{1}{3}\)?
A.
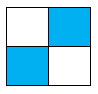
B.
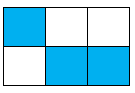
C.
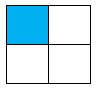
D.
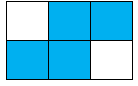
C.
- Xác định phân số chỉ phần tô đậm của mỗi hình.
- Quy đồng tử số hoặc mẫu số hai phân số, sau đó so sánh hai phân số sau khi quy đồng.
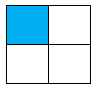
Phân số chỉ phần tô đậm của hình A là \(\dfrac{2}{4} = \dfrac{1}{2}\).
Phân số chỉ phần tô đậm của hình B là \(\dfrac{3}{6} = \dfrac{1}{2}\).
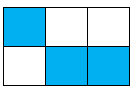
Phân số chỉ phần tô đậm của hình C là \(\dfrac{1}{4}\).
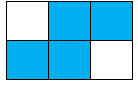
Phân số chỉ phần tô đậm của hình D là \(\dfrac{4}{6} = \dfrac{2}{3}\).
Ta có: \(\dfrac{1}{2} > \dfrac{1}{3}\) (vì \(2 < 3\)) nên \(\dfrac{2}{4} > \dfrac{1}{3}\,\,\,;\,\,\,\,\,\dfrac{3}{6} > \dfrac{1}{3}\).
\(\dfrac{1}{4} < \dfrac{1}{3}\) (vì \(4 > 3\)) .
\(\dfrac{2}{3} > \dfrac{1}{3}\) (vì \(2 > 1\)) nên \(\dfrac{4}{6}\,\, > \dfrac{1}{3}\).
Do đó phân số bé hơn \(\dfrac{1}{3}\) là \(\dfrac{1}{4}\).
Vậy hình C có phân số chỉ phần tô đậm bé hơn \(\dfrac{1}{3}\).

Rút gọn rồi so sánh hai phân số \(\dfrac{{120}}{{162}}\) và \(\dfrac{{108}}{{135}}\).
Vậy phân số lớn hơn là:
A. \(\dfrac{{120}}{{162}}\)
B. \(\dfrac{{108}}{{135}}\)
B. \(\dfrac{{108}}{{135}}\)
- Rút gọn hai phân số đã cho thành phân số tối giản
- So sánh hai phân số mới. Nếu hai phân số mới có cùng tử số hoặc mẫu số thì ta áp dụng quy tắc để so sánh luôn, ngược lại thì ta quy đồng tử số hoặc mẫu số để so sánh.
Rút gọn hai phân số đã cho ta có:
$\begin{array}{l}\dfrac{{120}}{{162}} = \dfrac{{120:2}}{{162:2}} = \dfrac{{60}}{{81}} = \dfrac{{60:3}}{{81:3}} = \dfrac{{20}}{{27}};\,\,\,\,\,\,\,\,\,\,\,\,\,\\\dfrac{{108}}{{135}} = \dfrac{{108:9}}{{135:9}} = \dfrac{{12}}{{15}} = \dfrac{{12:3}}{{15:3}} = \dfrac{4}{5} \cdot \end{array}$
Ta sẽ so sánh hai phân số \(\dfrac{{20}}{{27}}\) và \(\dfrac{4}{5}\) bằng cách quy đồng tử số.
Chọn tử số chung là \(20\).
Giữ nguyên phân số \(\dfrac{{20}}{{27}}\); \(\dfrac{4}{5} = \dfrac{{4 \times 5}}{{5 \times 5}} = \dfrac{{20}}{{25}}\)
Mà \(\dfrac{{20}}{{27}} < \dfrac{{20}}{{25}}\) (vì \(27 > 25\)).
Do đó \(\dfrac{{20}}{{27}} < \dfrac{4}{5}\) , hay \(\dfrac{{120}}{{162}} < \dfrac{{108}}{{135}}\)
Vậy phân số lớn hơn là \(\dfrac{{108}}{{135}}\).

Chọn phân số bé hơn trong hai phân số sau:
A. \(\dfrac{2}{{87}}\)
B. \(\dfrac{3}{{131}}\)
B. \(\dfrac{3}{{131}}\)
Quy đồng tử số hai phân số, sau đó so sánh hai phân số sau khi quy đồng.
TSC = \(6\).
Quy đồng tử số hai phân số ta có:
\(\dfrac{2}{{87}} = \dfrac{{2 \times 3}}{{87 \times 3}} = \dfrac{6}{{261}}\);
\(\dfrac{3}{{131}} = \dfrac{{3 \times 2}}{{131 \times 2}} = \dfrac{6}{{262}}\)
Mà \(\dfrac{6}{{261}} > \dfrac{6}{{262}}\) (vì \(261 < 262\))
Do đó \(\dfrac{2}{{87}} > \dfrac{3}{{131}}\)
Vậy phân số bé hơn là \(\dfrac{3}{{131}}\).

Chọn dấu thích hợp để điền vào chỗ chấm:
\(\dfrac{7}{8} \cdot \cdot \cdot \dfrac{3}{8}\)
A. \( > \)
B. \( < \)
C. \( = \)

Phân số nào dưới đây bé hơn phân số \(\dfrac{4}{9}\)?
A. \(\dfrac{7}{9}\)
B. \(\dfrac{8}{9}\)
C. \(\dfrac{3}{9}\)
D. \(\dfrac{5}{9}\)

Điền dấu (\(<;\,>;\,=\)) thích hợp vào ô trống:
\(\dfrac{7}{9}\,\,\)
\(\,\dfrac{{35}}{{45}}\)

Chọn dấu thích hợp để điền vào chỗ chấm:
\(\dfrac{3}{5} \cdot \cdot \cdot \dfrac{5}{6}\)
A. \( < \)
B. \( > \)
C. \( = \)

\(\dfrac{{13}}{{36}} \cdot \cdot \cdot \dfrac{{13}}{{25}}\)
Dấu thích hợp điền vào chỗ chấm là:
A. \( = \)
B. \( > \)
C. \( < \)

Hoa ăn \(\dfrac{5}{8}\) cái bánh, Lan ăn \(\dfrac{3}{5}\) cái bánh. Hỏi ai ăn nhiều bánh hơn?
A. Hoa
B. Lan
C. Hai bạn ăn bằng nhau

Hình nào dưới đây có phân số chỉ phần tô đậm bé hơn \(\dfrac{1}{3}\)?
A.

B.

C.

D.


Rút gọn rồi so sánh hai phân số \(\dfrac{{120}}{{162}}\) và \(\dfrac{{108}}{{135}}\).
Vậy phân số lớn hơn là:
A. \(\dfrac{{120}}{{162}}\)
B. \(\dfrac{{108}}{{135}}\)

Chọn phân số bé hơn trong hai phân số sau:
A. \(\dfrac{2}{{87}}\)
B. \(\dfrac{3}{{131}}\)

Chọn dấu thích hợp để điền vào chỗ chấm:
\(\dfrac{7}{8} \cdot \cdot \cdot \dfrac{3}{8}\)
A. \( > \)
B. \( < \)
C. \( = \)
A. \( > \)
Áp dụng quy tắc so sánh hai phân số có cùng mẫu số:
Trong hai phân số có cùng mẫu số:
+) Phân số nào có tử số bé hơn thì phân số đó bé hơn.
+) Phân số nào có tử số lớn hơn thì phân số đó lớn hơn.
+) Nếu tử số bằng nhau thì hai phân số đó bằng nhau.
Ta thấy hai phân số \(\dfrac{7}{8}\) và \(\dfrac{3}{8}\) đều có mẫu số là \(8\) và \(7 > 3\) nên \(\dfrac{7}{8} > \dfrac{3}{8}\).
Vậy dấu thích hợp điền vào chỗ chấm là \(>\).

Phân số nào dưới đây bé hơn phân số \(\dfrac{4}{9}\)?
A. \(\dfrac{7}{9}\)
B. \(\dfrac{8}{9}\)
C. \(\dfrac{3}{9}\)
D. \(\dfrac{5}{9}\)
C. \(\dfrac{3}{9}\)
Áp dụng quy tắc so sánh hai phân số có cùng mẫu số.
Ta thấy các phân số đã cho đều có mẫu số là \(9\) và \(3 < 4 < 7 < 8\) nên \(\dfrac{3}{9} < \dfrac{4}{9} < \dfrac{7}{9} < \dfrac{8}{9}\).
Vậy phân số bé hơn \(\dfrac{4}{9}\) là \(\dfrac{3}{9}\).

Điền dấu (\(<;\,>;\,=\)) thích hợp vào ô trống:
\(\dfrac{7}{9}\,\,\)
\(\,\dfrac{{35}}{{45}}\)
\(\dfrac{7}{9}\,\,\)
=\(\,\dfrac{{35}}{{45}}\)
Quy đồng mẫu số hai phân số, sau đó so sánh hai phân số sau khi quy đồng.
\(MSC = 45\).
Quy đồng mẫu số hai phân số ta có:
\(\dfrac{7}{9} = \dfrac{{7 \times 5}}{{9 \times 5}} = \dfrac{{35}}{{45}}\) Giữ nguyên phân số \(\dfrac{{35}}{{45}}\).
Ta thấy \(\dfrac{{35}}{{45}}\, = \,\dfrac{{35}}{{45}}\) nên \(\dfrac{7}{9}\, = \,\dfrac{{35}}{{45}}\)
Vậy dấu thích hợp điền vào ô trống là dấu \( = \).

Chọn dấu thích hợp để điền vào chỗ chấm:
\(\dfrac{3}{5} \cdot \cdot \cdot \dfrac{5}{6}\)
A. \( < \)
B. \( > \)
C. \( = \)
A. \( < \)
Quy đồng mẫu số hai phân số, sau đó so sánh hai phân số sau khi quy đồng.
\(MSC = 30\).
Quy đồng mẫu số hai phân số ta có:
\(\dfrac{3}{5} = \dfrac{{3 \times 6}}{{5 \times 6}} = \dfrac{{18}}{{30}};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{5}{6} = \dfrac{{5 \times 5}}{{6 \times 5}} = \dfrac{{25}}{{30}}\)
Mà \(\dfrac{{18}}{{30}} < \dfrac{{25}}{{30}}\) (vì \(18 < 25\)).
Vậy \(\dfrac{3}{5} < \dfrac{5}{6}\).

\(\dfrac{{13}}{{36}} \cdot \cdot \cdot \dfrac{{13}}{{25}}\)
Dấu thích hợp điền vào chỗ chấm là:
A. \( = \)
B. \( > \)
C. \( < \)
C. \( < \)
Dựa vào quy tắc so sánh hai phân số có cùng tử số:
Trong hai phân số có cùng tử số:
+) Phân số nào có mẫu số bé hơn thì phân số đó lớn hơn.
+) Phân số nào có mẫu số lớn hơn thì phân số đó bé hơn.
+) Nếu mẫu số bằng nhau thì hai phân số đó bằng nhau.
Ta thấy hai phân số \(\dfrac{{13}}{{36}}\) và \(\dfrac{{13}}{{25}}\) đều có tử số là \(13\) và \(36 > 25\) nên \(\dfrac{{13}}{{36}} < \dfrac{{13}}{{25}}\).
Vậy dấu thích hợp điền vào chỗ chấm là \(<\).

Hoa ăn \(\dfrac{5}{8}\) cái bánh, Lan ăn \(\dfrac{3}{5}\) cái bánh. Hỏi ai ăn nhiều bánh hơn?
A. Hoa
B. Lan
C. Hai bạn ăn bằng nhau
A. Hoa
Quy đồng mẫu số hai phân số chỉ số bánh hai bạn đã ăn, sau đó so sánh hai phân số sau khi quy đồng.
Ta sẽ so sánh hai phân số: \(\dfrac{5}{8}\) và \(\dfrac{3}{5}\).
$MSC = 40$
Quy đồng mẫu số hai phân số ta có:
\(\dfrac{5}{8} = \dfrac{{5 \times 5}}{{8 \times 5}} = \dfrac{{25}}{{40}}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{3}{5} = \dfrac{{3 \times 8}}{{5 \times 8}} = \dfrac{{24}}{{40}}\)
Mà \(\dfrac{{25}}{{40}} > \dfrac{{24}}{{40}}\) (vì \(25 > 24\) )
Do đó: \(\dfrac{5}{8} > \dfrac{3}{5}\)
Vậy Hoa ăn nhiều bánh hơn.

Hình nào dưới đây có phân số chỉ phần tô đậm bé hơn \(\dfrac{1}{3}\)?
A.

B.

C.

D.

C.

- Xác định phân số chỉ phần tô đậm của mỗi hình.
- Quy đồng tử số hoặc mẫu số hai phân số, sau đó so sánh hai phân số sau khi quy đồng.
Phân số chỉ phần tô đậm của hình A là \(\dfrac{2}{4} = \dfrac{1}{2}\).
Phân số chỉ phần tô đậm của hình B là \(\dfrac{3}{6} = \dfrac{1}{2}\).
Phân số chỉ phần tô đậm của hình C là \(\dfrac{1}{4}\).
Phân số chỉ phần tô đậm của hình D là \(\dfrac{4}{6} = \dfrac{2}{3}\).
Ta có: \(\dfrac{1}{2} > \dfrac{1}{3}\) (vì \(2 < 3\)) nên \(\dfrac{2}{4} > \dfrac{1}{3}\,\,\,;\,\,\,\,\,\dfrac{3}{6} > \dfrac{1}{3}\).
\(\dfrac{1}{4} < \dfrac{1}{3}\) (vì \(4 > 3\)) .
\(\dfrac{2}{3} > \dfrac{1}{3}\) (vì \(2 > 1\)) nên \(\dfrac{4}{6}\,\, > \dfrac{1}{3}\).
Do đó phân số bé hơn \(\dfrac{1}{3}\) là \(\dfrac{1}{4}\).
Vậy hình C có phân số chỉ phần tô đậm bé hơn \(\dfrac{1}{3}\).

Rút gọn rồi so sánh hai phân số \(\dfrac{{120}}{{162}}\) và \(\dfrac{{108}}{{135}}\).
Vậy phân số lớn hơn là:
A. \(\dfrac{{120}}{{162}}\)
B. \(\dfrac{{108}}{{135}}\)
B. \(\dfrac{{108}}{{135}}\)
- Rút gọn hai phân số đã cho thành phân số tối giản
- So sánh hai phân số mới. Nếu hai phân số mới có cùng tử số hoặc mẫu số thì ta áp dụng quy tắc để so sánh luôn, ngược lại thì ta quy đồng tử số hoặc mẫu số để so sánh.
Rút gọn hai phân số đã cho ta có:
$\begin{array}{l}\dfrac{{120}}{{162}} = \dfrac{{120:2}}{{162:2}} = \dfrac{{60}}{{81}} = \dfrac{{60:3}}{{81:3}} = \dfrac{{20}}{{27}};\,\,\,\,\,\,\,\,\,\,\,\,\,\\\dfrac{{108}}{{135}} = \dfrac{{108:9}}{{135:9}} = \dfrac{{12}}{{15}} = \dfrac{{12:3}}{{15:3}} = \dfrac{4}{5} \cdot \end{array}$
Ta sẽ so sánh hai phân số \(\dfrac{{20}}{{27}}\) và \(\dfrac{4}{5}\) bằng cách quy đồng tử số.
Chọn tử số chung là \(20\).
Giữ nguyên phân số \(\dfrac{{20}}{{27}}\); \(\dfrac{4}{5} = \dfrac{{4 \times 5}}{{5 \times 5}} = \dfrac{{20}}{{25}}\)
Mà \(\dfrac{{20}}{{27}} < \dfrac{{20}}{{25}}\) (vì \(27 > 25\)).
Do đó \(\dfrac{{20}}{{27}} < \dfrac{4}{5}\) , hay \(\dfrac{{120}}{{162}} < \dfrac{{108}}{{135}}\)
Vậy phân số lớn hơn là \(\dfrac{{108}}{{135}}\).

Chọn phân số bé hơn trong hai phân số sau:
A. \(\dfrac{2}{{87}}\)
B. \(\dfrac{3}{{131}}\)
B. \(\dfrac{3}{{131}}\)
Quy đồng tử số hai phân số, sau đó so sánh hai phân số sau khi quy đồng.
TSC = \(6\).
Quy đồng tử số hai phân số ta có:
\(\dfrac{2}{{87}} = \dfrac{{2 \times 3}}{{87 \times 3}} = \dfrac{6}{{261}}\);
\(\dfrac{3}{{131}} = \dfrac{{3 \times 2}}{{131 \times 2}} = \dfrac{6}{{262}}\)
Mà \(\dfrac{6}{{261}} > \dfrac{6}{{262}}\) (vì \(261 < 262\))
Do đó \(\dfrac{2}{{87}} > \dfrac{3}{{131}}\)
Vậy phân số bé hơn là \(\dfrac{3}{{131}}\).
Trong chương trình Toán 4, việc so sánh hai phân số là một kỹ năng quan trọng. Bài 61 tập trung vào việc so sánh hai phân số có cùng mẫu số, một dạng bài tập cơ bản nhưng cần được nắm vững để làm nền tảng cho các bài toán phức tạp hơn.
Để so sánh hai phân số có cùng mẫu số, ta chỉ cần so sánh tử số của hai phân số đó. Phân số nào có tử số lớn hơn thì phân số đó lớn hơn.
Ví dụ: So sánh 2/5 và 3/5. Vì 3 > 2 nên 3/5 > 2/5.
Đây là dạng bài tập đơn giản nhất, yêu cầu học sinh chỉ cần xác định tử số lớn hơn để đưa ra kết luận.
Ví dụ: Chọn đáp án đúng: 4/7 ... 2/7 (A. <, B. >, C. =)
Đáp án: B. >
Dạng bài này yêu cầu học sinh phải tính toán giá trị của các biểu thức trước khi so sánh.
Ví dụ: Chọn đáp án đúng: (1 + 2)/5 ... (3 - 1)/5 (A. <, B. >, C. =)
Đáp án: C. =
Dạng bài này giúp học sinh hiểu rõ hơn về ứng dụng của việc so sánh phân số trong cuộc sống.
Ví dụ: Lan có 2/3 chiếc bánh, Mai có 1/3 chiếc bánh. Ai có nhiều bánh hơn?
Đáp án: Lan có nhiều bánh hơn.
Để giải các bài tập trắc nghiệm về so sánh hai phân số cùng mẫu số, học sinh cần:
Để củng cố kiến thức và kỹ năng, học sinh có thể tự luyện tập thêm các bài tập sau:
| STT | Bài tập | Đáp án |
|---|---|---|
| 1 | So sánh 5/9 và 2/9 | 5/9 > 2/9 |
| 2 | So sánh (4 + 1)/8 và (2 + 3)/8 | (4 + 1)/8 > (2 + 3)/8 |
| 3 | Bình có 3/7 số kẹo, An có 5/7 số kẹo. Ai có nhiều kẹo hơn? | An có nhiều kẹo hơn |
Việc nắm vững kiến thức về so sánh hai phân số cùng mẫu số là rất quan trọng đối với học sinh lớp 4. Thông qua các bài tập trắc nghiệm và luyện tập, học sinh sẽ tự tin hơn trong việc giải các bài toán liên quan đến phân số. Giaitoan.edu.vn hy vọng sẽ là người bạn đồng hành đáng tin cậy trên con đường học tập của các em.