Chào mừng các em học sinh đến với đề thi giữa kì 1 Toán 7 - Đề số 10 của giaitoan.edu.vn. Đề thi này được thiết kế để giúp các em ôn luyện và củng cố kiến thức đã học trong chương trình Toán 7, chuẩn bị tốt nhất cho kỳ thi sắp tới.
Đề thi bao gồm các dạng bài tập khác nhau, từ cơ bản đến nâng cao, giúp các em làm quen với nhiều dạng câu hỏi và rèn luyện kỹ năng giải toán.
Phần trắc nghiệm (3 điểm) Câu 1: Chọn đáp án đúng
Phần trắc nghiệm (3 điểm)
Câu 1: Chọn đáp án đúng
A. \( - 7 \in \mathbb{N}\)
B. \( - 7 \notin \mathbb{Z}\)
C. \( - 7 \notin \mathbb{Q}\)
D. \(\frac{1}{2} \in \mathbb{Q}\)
Câu 2: Kết quả của phép tính: \(\frac{{ - 3}}{{20}} + \frac{{ - 2}}{{15}}\) là
A. \(\frac{{ - 1}}{{60}}\)
B. \(\frac{{ - 17}}{{60}}\)
C. \(\frac{{ - 5}}{{35}}\)
D. \(\frac{1}{{60}}\)
Câu 3: Kết quả của phép tính: - 0,35. \(\frac{2}{7}\) là
A. - 0,1
B. -1
C. -10
D. -100
Câu 4: Kết quả của phép tính: \(\frac{{ - 26}}{{15}}:2\frac{3}{5}\) là
A. -6
B. \(\frac{{ - 3}}{2}\)
C. \(\frac{{ - 2}}{3}\)
D. \(\frac{{ - 3}}{4}\)
Câu 5: Kết quả phép tính: \(\frac{3}{4} + \frac{1}{4}.\frac{{ - 12}}{{20}}\) là
A. \(\frac{{ - 12}}{{20}}\)
B. \(\frac{3}{5}\)
C. \(\frac{{ - 3}}{5}\)
D. \(\frac{{ - 9}}{{84}}\)
Câu 6: Giá trị của biểu thức : | - 3,4 | : | +1,7 | - 0,2 là
A. - 1,8
B. 1,8
C. 0
D. - 2,2
Câu 7: Kết quả phép tính: \({\left( { - \frac{1}{3}} \right)^4}\)
A. \(\frac{1}{{81}}\).
B. \(\frac{4}{{81}}\).
C. \(\frac{{ - 1}}{{81}}\).
D. \(\frac{{ - 4}}{{81}}\).
Câu 8: Trong hình dưới đây có bao nhiêu hình lập phương, bao nhiêu hình hộp chữ nhật?
A. 2 hình lập phương, 3 hình hộp chữ nhật;
B. 1 hình lập phương, 3 hình hộp chữ nhật;
C. 2 hình lập phương, 2 hình hộp chữ nhật;
D. 0 hình lập phương, 4 hình hộp chữ nhật.
Câu 9: Hãy chọn khẳng định sai. Hình lập phương ABCD.A'B'C'D' có:
A. 8 đỉnh
B. 4 mặt bên
C. 6 cạnh
D. 6 mặt
Câu 10: Cho hình hộp chữ nhật ABCD. EFGH. Cho AB = 4 cm, BC = 2 cm, AE = 4 cm. Khẳng định đúng là:
A. HG = 4 cm, HE = 2 cm, GC = 4 cm;
B. HG = 2 cm, HE = 2 cm, GC = 4 cm;
C. HG = 4 cm, HE = 2 cm, GC = 2 cm;
D. HG = 4 cm, HE = 4 cm, GC = 4 cm.
Câu 11: Tấm bìa bên dưới có thể tạo lập thành một hình lăng trụ đứng có đáy là tam giác đều.
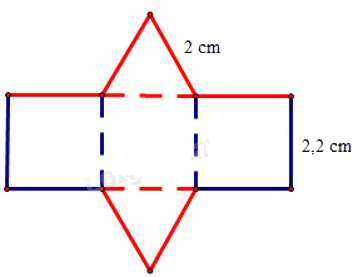
Chiều cao của hình lăng trụ đứng là:
A. 2 cm
B. 2,2 cm
C. 4 cm
D. 4,4 cm
Câu 12: Chọn phát biểu sai:
A. Hai góc đối đỉnh thì bằng nhau;
B. Hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia được gọi là hai gócđối đỉnh;
C. Hai đường thẳng cắt nhau tại một điểm tạo thành hai cặp góc đối đỉnh;
D. Hai góc bằng nhau thì đối đỉnh.
Phần tự luận (7 điểm)
Bài 1: (1 điểm) Tìm x, biết
a. \(x - \frac{3}{4} = \frac{5}{{ - 7}}\)
b. 100 - \(\left| {x + 1} \right| = 90\)
Bài 2. (1,5 điểm) Thực hiện phép tính:
a) \(\frac{2}{3}:\frac{{ - 6}}{9} + \frac{1}{7}\);
b) \(\frac{{ - 3}}{{11}} \cdot \frac{5}{9} + \frac{4}{9} \cdot \frac{{ - 3}}{{11}}\);
c) \(\frac{{{9^5}{{.8}^2}}}{{{{27}^3}.16}}\).
Bài 3. (1 điểm) Bác Long có một căn phòng hình hộp chữ nhật có một cửa ra vào và mộtcửa sổ hình vuông với các kích thước như hình vẽ.
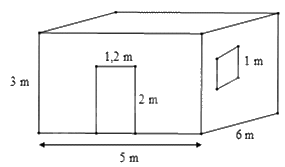
Hỏi bác Long cần trả bao nhiêu chi phí để sơn bốn bức tường xung quanh của căn phòng này (không sơn cửa)? Biết rằng để sơn mỗi mét vuông tốn 30 nghìn đồng.
Bài 4. (1,5 điểm) Một khối gỗ có dạng hình lăng trụ đứng đáy là tam giác vuông có kích thướcthước hai cạnh góc vuông là 3 dm; 4 dm, cạnh huyền (cạnh đối diện với góc vuông) là 0,5 m.Người ta khoét một lỗ lăng trụ đứng đáy tam giác vuông hai cạnh góc vuông có kích thước là 1,5 dm; 2 dm; cạnh huyền 2,5 dm. Biết khối gỗ dài 0,45 m (hình vẽ).
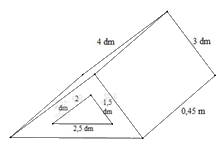
a) Tính thể tích của khối gỗ.b) Người ta muốn sơn tất cả các bề mặt của khối gỗ. Tính diện tích cần sơn (đơn vị mét vuông).
Bài 5. (1,5 điểm) Cho hình vẽ dưới đây:
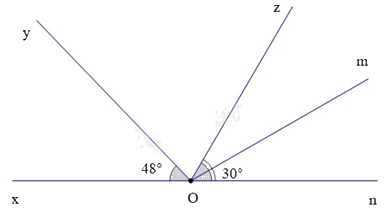Biết rằng \(\widehat {xOy} = {48^0},\widehat {mOn} = {30^0}\) và Om là phân giác của \(\widehat {zOn}\).a) Kể tên các góc (khác góc bẹt) kề với \(\widehat {zOm}\); góc kề bù với \(\widehat {mOn}\).b) Tính số đo của góc \(\widehat {yOz}\).
Bài 6. (0,5 điểm) Tìm hai số x, y. Tính giá trị nhỏ nhất của biểu thức: \({\rm{M}} = {({\rm{x}} - 5)^2} + 7\)
-------- Hết --------
Phần trắc nghiệm (3 điểm)
Câu 1: D | Câu 2: B | Câu 3: A | Câu 4: C | Câu 5: B | Câu 6: B |
Câu 7. A | Câu 8. B | Câu 9. C | Câu 10. A | Câu 11. B | Câu 12. D |
Câu 1: Chọn đáp án đúng
A. \( - 7 \in \mathbb{N}\) | B. \( - 7 \notin \mathbb{Z}\) |
C. \( - 7 \notin \mathbb{Q}\) | D. \(\frac{1}{2} \in \mathbb{Q}\) |
Phương pháp
Dựa vào các tập hợp số đã học.
Lời giải
Ta có:
\( - 7 \notin \mathbb{N}\) nên A sai.
\( - 7 \in \mathbb{Z}\) nên B sai.
\( - 7 \in \mathbb{Q}\) nên C sai.
\(\frac{1}{2} \in \mathbb{Q}\) nên D đúng.
Đáp án D.
Câu 2: Kết quả của phép tính: \(\frac{{ - 3}}{{20}} + \frac{{ - 2}}{{15}}\) là
A. \(\frac{{ - 1}}{{60}}\) | B. \(\frac{{ - 17}}{{60}}\) |
C. \(\frac{{ - 5}}{{35}}\) | D. \(\frac{1}{{60}}\) |
Phương pháp
Sử dụng quy tắc cộng hai số hữu tỉ.
Lời giải
\(\frac{{ - 3}}{{20}} + \frac{{ - 2}}{{15}} = \frac{{ - 9 + \left( { - 8} \right)}}{{60}} = \frac{{ - 17}}{{60}}\)
Đáp án B.
Câu 3: Kết quả của phép tính: - 0,35. \(\frac{2}{7}\) là
A. - 0,1 | B. -1 |
C. -10 | D. -100 |
Phương pháp
Sử dụng quy tắc nhân số hữu tỉ.
Lời giải
\( - {\rm{ }}0,35.\;\frac{2}{7} = - \frac{7}{{20}}.\frac{2}{7} = - \frac{1}{{10}} = - 0,1\).
Đáp án A.
Câu 4: Kết quả của phép tính: \(\frac{{ - 26}}{{15}}:2\frac{3}{5}\) là
A. -6 | B. \(\frac{{ - 3}}{2}\) |
C. \(\frac{{ - 2}}{3}\) | D. \(\frac{{ - 3}}{4}\) |
Phương pháp
Sử dụng quy tắc chia số hữu tỉ.
Lời giải
\(\frac{{ - 26}}{{15}}:2\frac{3}{5} = \frac{{ - 26}}{{15}}:\frac{{13}}{5} = \frac{{ - 26}}{{15}}.\frac{5}{{13}} = \frac{{ - 2}}{3}\)
Đáp án C.
Câu 5: Kết quả phép tính: \(\frac{3}{4} + \frac{1}{4}.\frac{{ - 12}}{{20}}\) là
A. \(\frac{{ - 12}}{{20}}\) | B. \(\frac{3}{5}\) |
C. \(\frac{{ - 3}}{5}\) | D. \(\frac{{ - 9}}{{84}}\) |
Phương pháp
Sử dụng các quy tắc tính với số hữu tỉ.
Lời giải
\(\frac{3}{4} + \frac{1}{4}.\frac{{ - 12}}{{20}} = \frac{3}{4} + \frac{{ - 3}}{{20}} = \frac{3}{5}\).
Đáp án B.
Câu 6: Giá trị của biểu thức : | - 3,4 | : | +1,7 | - 0,2 là
A. - 1,8 | B. 1,8 |
C. 0 | D. - 2,2 |
Phương pháp
Xác định giá trị tuyệt đối của -3,4 và +1,7 để tính toán.
Lời giải
| - 3,4 | : | +1,7 | - 0,2 = 3,4 : 1,7 – 0,2 = 2 – 0,2 = 1,8.
Đáp án B.
Câu 7: Kết quả phép tính: \({\left( { - \frac{1}{3}} \right)^4}\)
A. \(\frac{1}{{81}}\). | B. \(\frac{4}{{81}}\). |
C. \(\frac{{ - 1}}{{81}}\). | D. \(\frac{{ - 4}}{{81}}\). |
Phương pháp
Dựa vào cách tính lũy thừa của một số.
Lời giải
\({\left( { - \frac{1}{3}} \right)^4} = \frac{1}{{81}}\).
Đáp án A.
Câu 8: Trong hình dưới đây có bao nhiêu hình lập phương, bao nhiêu hình hộp chữ nhật?
A. 2 hình lập phương, 3 hình hộp chữ nhật;B. 1 hình lập phương, 3 hình hộp chữ nhật;C. 2 hình lập phương, 2 hình hộp chữ nhật;D. 0 hình lập phương, 4 hình hộp chữ nhật.
Phương pháp
Quan sát hình vẽ để xác định số hình lập phương và hình hộp chữ nhật.
Lời giải
Quan sát hình trên ta thấy có 1 hình lập phương và 3 hình hộp chữ nhật.
Đáp án B.
Câu 9: Hãy chọn khẳng định sai. Hình lập phương ABCD.A'B'C'D' có:
A. 8 đỉnh | B. 4 mặt bên |
C. 6 cạnh | D. 6 mặt |
Phương pháp
Dựa vào kiến thức về hình lập phương.
Lời giải
Hình lập phương có 8 đỉnh nên A đúng.
Hình lập phương có 4 mặt bên và 2 mặt đáy => có tổng 6 mặt nên B và D đúng.
Hình lập phương có 8 cạnh đáy và 4 cạnh bên => có 12 cạnh nên C sai.
Đáp án C.
Câu 10: Cho hình hộp chữ nhật ABCD. EFGH. Cho AB = 4 cm, BC = 2 cm, AE = 4 cm. Khẳng định đúng là:A. HG = 4 cm, HE = 2 cm, GC = 4 cm;B. HG = 2 cm, HE = 2 cm, GC = 4 cm;C. HG = 4 cm, HE = 2 cm, GC = 2 cm;D. HG = 4 cm, HE = 4 cm, GC = 4 cm.
Phương pháp
Dựa vào tính chất các cạnh của hình hộp chữ nhật.
Lời giải
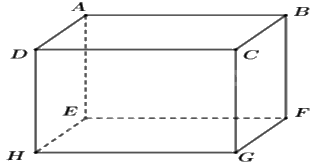
Hình hộp chữ nhật ABCD. EFGH có:
HG = AB = 4cm;
HE = BC = 2cm;
GC = AE = 4cm.
Đáp án A.
Câu 11: Tấm bìa bên dưới có thể tạo lập thành một hình lăng trụ đứng có đáy là tam giác đều.
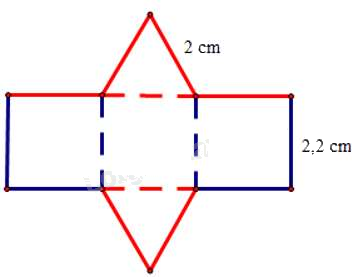
Chiều cao của hình lăng trụ đứng là:
A. 2 cm | B. 2,2 cm |
C. 4 cm | D. 4,4 cm |
Phương pháp
Quan sát hình vẽ.
Lời giải
Chiều cao của hình lăng trụ đứng là 2,2 cm.
Đáp án B.
Câu 12: Chọn phát biểu sai:A. Hai góc đối đỉnh thì bằng nhau;B. Hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia được gọi là hai gócđối đỉnh;C. Hai đường thẳng cắt nhau tại một điểm tạo thành hai cặp góc đối đỉnh;D. Hai góc bằng nhau thì đối đỉnh.
Phương pháp
Dựa vào kiến thức về hai góc đối đỉnh.
Lời giải
Hai góc bằng nhau chưa chắc đã là hai góc đối đỉnh nên đáp án D là đáp án sai.
Đáp án D.
Phần tự luận.
Bài 1: (1 điểm). Tìm x, biết
a. \(x - \frac{3}{4} = \frac{5}{{ - 7}}\) | b. 100 - \(\left| {x + 1} \right| = 90\) |
Phương pháp
Sử dụng quy tắc chuyển vế, kiến thức về giá trị tuyệt đối để giải tìm x.
Lời giải
a. \(x - \frac{3}{4} = \frac{5}{{ - 7}}\)
\(\begin{array}{l}x = \frac{5}{{ - 7}} + \frac{3}{4}\\x = \frac{1}{{28}}\end{array}\)
Vậy \(x = \frac{1}{{28}}\).
b. 100 - \(\left| {x + 1} \right| = 90\)
\(\begin{array}{l}|x + 1| = 100 - 90\\|x + 1| = 10\end{array}\)
=> x + 1 = 10 hoặc x + 1 = -10
hay x = 9 hoặc x = -11.
Vậy x = 9 hoặc x = -11.
Bài 2. (1,5 điểm). Thực hiện phép tính:
a) \(\frac{2}{3}:\frac{{ - 6}}{9} + \frac{1}{7}\); | b) \(\frac{{ - 3}}{{11}} \cdot \frac{5}{9} + \frac{4}{9} \cdot \frac{{ - 3}}{{11}}\); | c) \(\frac{{{9^5}{{.8}^2}}}{{{{27}^3}.16}}\). |
Phương pháp
Dựa vào quy tắc tính với số hữu tỉ và lũy thừa để tính.
Lời giải
a) \(\frac{2}{3}:\frac{{ - 6}}{9} + \frac{1}{7}\)
\( = \frac{2}{3}.\frac{{ - 9}}{6} + \frac{1}{7}\)\( = - 1 + \frac{1}{7}\)\( = \frac{{ - 6}}{7}\).
b) \(\frac{{ - 3}}{{11}} \cdot \frac{5}{9} + \frac{4}{9} \cdot \frac{{ - 3}}{{11}}\)
\( = \frac{{ - 3}}{{11}} \cdot \left( {\frac{5}{9} + \frac{4}{9}} \right)\)\( = \frac{{ - 3}}{{11}}.1\)\( = \frac{{ - 3}}{{11}}\).
c) \(\frac{{{9^5}{{.8}^2}}}{{{{27}^3}.16}}\)
\( = \frac{{{{\left( {{3^2}} \right)}^5}.{{\left( {{2^3}} \right)}^2}}}{{{{\left( {{3^3}} \right)}^3}{{.2}^4}}}\)\( = \frac{{{3^{10}}{{.2}^6}}}{{{3^9}{{.2}^4}}}\)\( = {3.2^2} = 3.4 = 12\)
Bài 3. (1 điểm) Bác Long có một căn phòng hình hộp chữ nhật có một cửa ra vào và mộtcửa sổ hình vuông với các kích thước như hình vẽ.
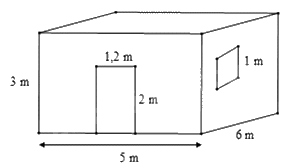
Hỏi bác Long cần trả bao nhiêu chi phí để sơn bốn bức tường xung quanh của căn phòng này(không sơn cửa)? Biết rằng để sơn mỗi mét vuông tốn 30 nghìn đồng.
Phương pháp
- Tính diện tích phần cần sơn:
Diện tích phần cần sơn = Diện tích xung quanh của căn phòng – Diện tích các cửa.
- Tính số tiền bác Long dùng để sơn căn phòng:
Số tiền dùng để sơn = diện tích phần cần sơn . chi phí sơn mỗi mét vuông.
Lời giải
Diện tích xung quanh của căn phòng là: Sxq = 2.(5 + 6).3 = 66(m2).Diện tích phần cửa lớn và cửa sổ là: 1,2 . 2 + 1 . 1 = 3,4 (m2).Diện tích phần cần sơn là: 66 – 3,4 = 62,6 (m2)Tổng chi phí cần để sơn là: 62,6. 30 000 = 1 878 000 (đồng).Vậy bác Long cần 1 878 000 đồng để sơn bốn bức tường xung quanh của căn phòng này.
Bài 4. (1,5 điểm) Một khối gỗ có dạng hình lăng trụ đứng đáy là tam giác vuông có kích thướcthước hai cạnh góc vuông là 3 dm; 4 dm, cạnh huyền (cạnh đối diện với góc vuông) là 0,5 m.Người ta khoét một lỗ lăng trụ đứng đáy tam giác vuông hai cạnh góc vuông có kích thước là1,5 dm; 2 dm; cạnh huyền 2,5 dm. Biết khối gỗ dài 0,45 m (hình vẽ).
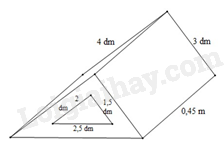
a) Tính thể tích của khối gỗ.b) Người ta muốn sơn tất cả các bề mặt của khối gỗ. Tính diện tích cần sơn (đơn vị mét vuông).
Phương pháp
a) Sử dụng công thức tính thể tích hình lăng trụ đứng.
b) Tính diện tích xung quanh khối kim loại, diện tích xung quanh lỗ, diện tích đáy.
Diện tích bề mặt cần sơn = diện tích xung quanh của khối gỗ + diện tích xung quanh của cái lỗ - diện tích hai đáy trừ đi diện tích hai cái đáy lỗ.
Lời giải
Đổi: 3 dm = 30 cm; 4 dm = 40 cm; 0,5 m = 50 cm;1,5 dm = 15 cm; 2 dm = 20 cm; 2,5 dm = 25 cm; 0,45 m = 45 cm.a) Thể tích khối gỗ là: \(\frac{1}{2}.40.30.45 - \frac{1}{2}.20.15.45{\rm{ }} = {\rm{ }}20250\)(cm3)b) Diện tích xung quanh của gỗ là: (30 + 40 + 50).45 = 5400(cm2)Diện tích xung quanh của cái lỗ là: (20 +15 + 25).45 = 2700(cm2)Diện tích hai đáy trừ đi diện tích hai cái đáy lỗ là:
\(\frac{1}{2}.30.40 - \frac{1}{2}.15.20 = 450\)(cm2)
Diện tích bề mặt cần sơn là: 5400 + 2700 - 450 = 7650(cm2) = 0,765(m2)Vậy diện tích cần sơn là 0,765m2.
Bài 5. (1,5 điểm) Cho hình vẽ dưới đây:
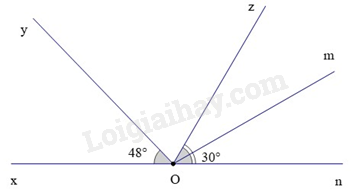Biết rằng \(\widehat {xOy} = {48^0},\widehat {mOn} = {30^0}\) và Om là phân giác của \(\widehat {zOn}\).a) Kể tên các góc (khác góc bẹt) kề với \(\widehat {zOm}\); góc kề bù với \(\widehat {mOn}\).b) Tính số đo của góc \(\widehat {yOz}\).
Phương pháp
a) Hai góc kề nhau là các góc có một cạnh chung và không có điểm trong chung; hai góc kề bù là hai góc kề nhau và có tổng bằng 1800.
b) \(\widehat {yOz} = 180 - \widehat {xOy} - \widehat {nOz}\).
Lời giải
a) Các góc (khác góc bẹt) kề với \(\widehat {zOm}\) là \(\widehat {zOy}\), \(\widehat {zOx}\), \(\widehat {mOn}\).Góc kề bù với \(\widehat {mOn}\) là \(\widehat {mOx}\).
b) Theo bài ta có Om là tia phân giác của \(\widehat {zOn}\).
Suy ra \(\widehat {zOm} = \widehat {mOn}\) (tính chất tia phân giác của một góc) (1)Mà \(\widehat {zOm} + \widehat {mOn} = \widehat {zOn}\) (hai góc kề nhau) (2)Từ (1) và (2) suy ra \(\widehat {zOm} = \widehat {mOn} = \frac{{\widehat {zOn}}}{2} \Rightarrow \widehat {zOn} = 2\widehat {mOn} = {2.30^0} = {60^0}\)Ta có \(\widehat {xOy} + \widehat {yOz} + \widehat {zOn} = \widehat {xOn} = {180^0}\)
Hay \({48^0} + \widehat {yOz} + {60^0} = {180^0} \Rightarrow \widehat {yOz} = {180^0} - {48^0} - {60^0} = {72^0}\)Vậy số đo của \(\widehat {yOz} = {72^0}\).
Bài 6. (0,5 điểm). Tìm hai số x, y. Tính giá trị nhỏ nhất của biểu thức: \({\rm{M}} = {({\rm{x}} - 5)^2} + 7\)
Phương pháp
Dựa vào đặc điểm của biểu thức (x – 5)2.
Lời giải
Ta có \({\left( {x - 5} \right)^2} \ge 0,\,\forall x \in \mathbb{R}\) nên \({\left( {x - 5} \right)^2} + 7 \ge 7,\,\forall x \in \mathbb{R}\) hay \(M \ge 7\). Dấu “=” xảy ra khi và chỉ khi \({\left( {x - 5} \right)^2} = 0 \Leftrightarrow x = 5\).
Vậy giá trị nhỏ nhất của M là 7 khi x = 5.
Tải về
Phần trắc nghiệm (3 điểm)
Câu 1: Chọn đáp án đúng
A. \( - 7 \in \mathbb{N}\)
B. \( - 7 \notin \mathbb{Z}\)
C. \( - 7 \notin \mathbb{Q}\)
D. \(\frac{1}{2} \in \mathbb{Q}\)
Câu 2: Kết quả của phép tính: \(\frac{{ - 3}}{{20}} + \frac{{ - 2}}{{15}}\) là
A. \(\frac{{ - 1}}{{60}}\)
B. \(\frac{{ - 17}}{{60}}\)
C. \(\frac{{ - 5}}{{35}}\)
D. \(\frac{1}{{60}}\)
Câu 3: Kết quả của phép tính: - 0,35. \(\frac{2}{7}\) là
A. - 0,1
B. -1
C. -10
D. -100
Câu 4: Kết quả của phép tính: \(\frac{{ - 26}}{{15}}:2\frac{3}{5}\) là
A. -6
B. \(\frac{{ - 3}}{2}\)
C. \(\frac{{ - 2}}{3}\)
D. \(\frac{{ - 3}}{4}\)
Câu 5: Kết quả phép tính: \(\frac{3}{4} + \frac{1}{4}.\frac{{ - 12}}{{20}}\) là
A. \(\frac{{ - 12}}{{20}}\)
B. \(\frac{3}{5}\)
C. \(\frac{{ - 3}}{5}\)
D. \(\frac{{ - 9}}{{84}}\)
Câu 6: Giá trị của biểu thức : | - 3,4 | : | +1,7 | - 0,2 là
A. - 1,8
B. 1,8
C. 0
D. - 2,2
Câu 7: Kết quả phép tính: \({\left( { - \frac{1}{3}} \right)^4}\)
A. \(\frac{1}{{81}}\).
B. \(\frac{4}{{81}}\).
C. \(\frac{{ - 1}}{{81}}\).
D. \(\frac{{ - 4}}{{81}}\).
Câu 8: Trong hình dưới đây có bao nhiêu hình lập phương, bao nhiêu hình hộp chữ nhật?
A. 2 hình lập phương, 3 hình hộp chữ nhật;
B. 1 hình lập phương, 3 hình hộp chữ nhật;
C. 2 hình lập phương, 2 hình hộp chữ nhật;
D. 0 hình lập phương, 4 hình hộp chữ nhật.
Câu 9: Hãy chọn khẳng định sai. Hình lập phương ABCD.A'B'C'D' có:
A. 8 đỉnh
B. 4 mặt bên
C. 6 cạnh
D. 6 mặt
Câu 10: Cho hình hộp chữ nhật ABCD. EFGH. Cho AB = 4 cm, BC = 2 cm, AE = 4 cm. Khẳng định đúng là:
A. HG = 4 cm, HE = 2 cm, GC = 4 cm;
B. HG = 2 cm, HE = 2 cm, GC = 4 cm;
C. HG = 4 cm, HE = 2 cm, GC = 2 cm;
D. HG = 4 cm, HE = 4 cm, GC = 4 cm.
Câu 11: Tấm bìa bên dưới có thể tạo lập thành một hình lăng trụ đứng có đáy là tam giác đều.
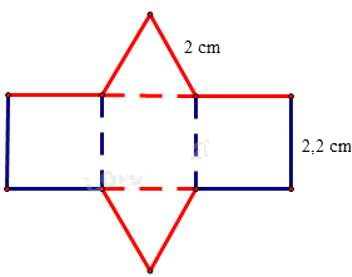
Chiều cao của hình lăng trụ đứng là:
A. 2 cm
B. 2,2 cm
C. 4 cm
D. 4,4 cm
Câu 12: Chọn phát biểu sai:
A. Hai góc đối đỉnh thì bằng nhau;
B. Hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia được gọi là hai gócđối đỉnh;
C. Hai đường thẳng cắt nhau tại một điểm tạo thành hai cặp góc đối đỉnh;
D. Hai góc bằng nhau thì đối đỉnh.
Phần tự luận (7 điểm)
Bài 1: (1 điểm) Tìm x, biết
a. \(x - \frac{3}{4} = \frac{5}{{ - 7}}\)
b. 100 - \(\left| {x + 1} \right| = 90\)
Bài 2. (1,5 điểm) Thực hiện phép tính:
a) \(\frac{2}{3}:\frac{{ - 6}}{9} + \frac{1}{7}\);
b) \(\frac{{ - 3}}{{11}} \cdot \frac{5}{9} + \frac{4}{9} \cdot \frac{{ - 3}}{{11}}\);
c) \(\frac{{{9^5}{{.8}^2}}}{{{{27}^3}.16}}\).
Bài 3. (1 điểm) Bác Long có một căn phòng hình hộp chữ nhật có một cửa ra vào và mộtcửa sổ hình vuông với các kích thước như hình vẽ.
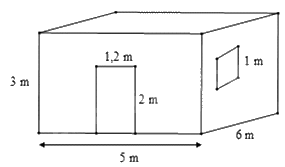
Hỏi bác Long cần trả bao nhiêu chi phí để sơn bốn bức tường xung quanh của căn phòng này (không sơn cửa)? Biết rằng để sơn mỗi mét vuông tốn 30 nghìn đồng.
Bài 4. (1,5 điểm) Một khối gỗ có dạng hình lăng trụ đứng đáy là tam giác vuông có kích thướcthước hai cạnh góc vuông là 3 dm; 4 dm, cạnh huyền (cạnh đối diện với góc vuông) là 0,5 m.Người ta khoét một lỗ lăng trụ đứng đáy tam giác vuông hai cạnh góc vuông có kích thước là 1,5 dm; 2 dm; cạnh huyền 2,5 dm. Biết khối gỗ dài 0,45 m (hình vẽ).
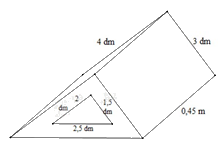
a) Tính thể tích của khối gỗ.b) Người ta muốn sơn tất cả các bề mặt của khối gỗ. Tính diện tích cần sơn (đơn vị mét vuông).
Bài 5. (1,5 điểm) Cho hình vẽ dưới đây:
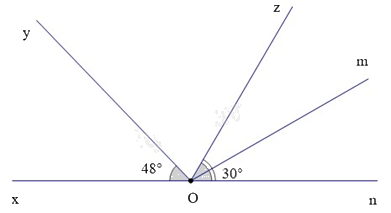Biết rằng \(\widehat {xOy} = {48^0},\widehat {mOn} = {30^0}\) và Om là phân giác của \(\widehat {zOn}\).a) Kể tên các góc (khác góc bẹt) kề với \(\widehat {zOm}\); góc kề bù với \(\widehat {mOn}\).b) Tính số đo của góc \(\widehat {yOz}\).
Bài 6. (0,5 điểm) Tìm hai số x, y. Tính giá trị nhỏ nhất của biểu thức: \({\rm{M}} = {({\rm{x}} - 5)^2} + 7\)
-------- Hết --------
Phần trắc nghiệm (3 điểm)
Câu 1: D | Câu 2: B | Câu 3: A | Câu 4: C | Câu 5: B | Câu 6: B |
Câu 7. A | Câu 8. B | Câu 9. C | Câu 10. A | Câu 11. B | Câu 12. D |
Câu 1: Chọn đáp án đúng
A. \( - 7 \in \mathbb{N}\) | B. \( - 7 \notin \mathbb{Z}\) |
C. \( - 7 \notin \mathbb{Q}\) | D. \(\frac{1}{2} \in \mathbb{Q}\) |
Phương pháp
Dựa vào các tập hợp số đã học.
Lời giải
Ta có:
\( - 7 \notin \mathbb{N}\) nên A sai.
\( - 7 \in \mathbb{Z}\) nên B sai.
\( - 7 \in \mathbb{Q}\) nên C sai.
\(\frac{1}{2} \in \mathbb{Q}\) nên D đúng.
Đáp án D.
Câu 2: Kết quả của phép tính: \(\frac{{ - 3}}{{20}} + \frac{{ - 2}}{{15}}\) là
A. \(\frac{{ - 1}}{{60}}\) | B. \(\frac{{ - 17}}{{60}}\) |
C. \(\frac{{ - 5}}{{35}}\) | D. \(\frac{1}{{60}}\) |
Phương pháp
Sử dụng quy tắc cộng hai số hữu tỉ.
Lời giải
\(\frac{{ - 3}}{{20}} + \frac{{ - 2}}{{15}} = \frac{{ - 9 + \left( { - 8} \right)}}{{60}} = \frac{{ - 17}}{{60}}\)
Đáp án B.
Câu 3: Kết quả của phép tính: - 0,35. \(\frac{2}{7}\) là
A. - 0,1 | B. -1 |
C. -10 | D. -100 |
Phương pháp
Sử dụng quy tắc nhân số hữu tỉ.
Lời giải
\( - {\rm{ }}0,35.\;\frac{2}{7} = - \frac{7}{{20}}.\frac{2}{7} = - \frac{1}{{10}} = - 0,1\).
Đáp án A.
Câu 4: Kết quả của phép tính: \(\frac{{ - 26}}{{15}}:2\frac{3}{5}\) là
A. -6 | B. \(\frac{{ - 3}}{2}\) |
C. \(\frac{{ - 2}}{3}\) | D. \(\frac{{ - 3}}{4}\) |
Phương pháp
Sử dụng quy tắc chia số hữu tỉ.
Lời giải
\(\frac{{ - 26}}{{15}}:2\frac{3}{5} = \frac{{ - 26}}{{15}}:\frac{{13}}{5} = \frac{{ - 26}}{{15}}.\frac{5}{{13}} = \frac{{ - 2}}{3}\)
Đáp án C.
Câu 5: Kết quả phép tính: \(\frac{3}{4} + \frac{1}{4}.\frac{{ - 12}}{{20}}\) là
A. \(\frac{{ - 12}}{{20}}\) | B. \(\frac{3}{5}\) |
C. \(\frac{{ - 3}}{5}\) | D. \(\frac{{ - 9}}{{84}}\) |
Phương pháp
Sử dụng các quy tắc tính với số hữu tỉ.
Lời giải
\(\frac{3}{4} + \frac{1}{4}.\frac{{ - 12}}{{20}} = \frac{3}{4} + \frac{{ - 3}}{{20}} = \frac{3}{5}\).
Đáp án B.
Câu 6: Giá trị của biểu thức : | - 3,4 | : | +1,7 | - 0,2 là
A. - 1,8 | B. 1,8 |
C. 0 | D. - 2,2 |
Phương pháp
Xác định giá trị tuyệt đối của -3,4 và +1,7 để tính toán.
Lời giải
| - 3,4 | : | +1,7 | - 0,2 = 3,4 : 1,7 – 0,2 = 2 – 0,2 = 1,8.
Đáp án B.
Câu 7: Kết quả phép tính: \({\left( { - \frac{1}{3}} \right)^4}\)
A. \(\frac{1}{{81}}\). | B. \(\frac{4}{{81}}\). |
C. \(\frac{{ - 1}}{{81}}\). | D. \(\frac{{ - 4}}{{81}}\). |
Phương pháp
Dựa vào cách tính lũy thừa của một số.
Lời giải
\({\left( { - \frac{1}{3}} \right)^4} = \frac{1}{{81}}\).
Đáp án A.
Câu 8: Trong hình dưới đây có bao nhiêu hình lập phương, bao nhiêu hình hộp chữ nhật?
A. 2 hình lập phương, 3 hình hộp chữ nhật;B. 1 hình lập phương, 3 hình hộp chữ nhật;C. 2 hình lập phương, 2 hình hộp chữ nhật;D. 0 hình lập phương, 4 hình hộp chữ nhật.
Phương pháp
Quan sát hình vẽ để xác định số hình lập phương và hình hộp chữ nhật.
Lời giải
Quan sát hình trên ta thấy có 1 hình lập phương và 3 hình hộp chữ nhật.
Đáp án B.
Câu 9: Hãy chọn khẳng định sai. Hình lập phương ABCD.A'B'C'D' có:
A. 8 đỉnh | B. 4 mặt bên |
C. 6 cạnh | D. 6 mặt |
Phương pháp
Dựa vào kiến thức về hình lập phương.
Lời giải
Hình lập phương có 8 đỉnh nên A đúng.
Hình lập phương có 4 mặt bên và 2 mặt đáy => có tổng 6 mặt nên B và D đúng.
Hình lập phương có 8 cạnh đáy và 4 cạnh bên => có 12 cạnh nên C sai.
Đáp án C.
Câu 10: Cho hình hộp chữ nhật ABCD. EFGH. Cho AB = 4 cm, BC = 2 cm, AE = 4 cm. Khẳng định đúng là:A. HG = 4 cm, HE = 2 cm, GC = 4 cm;B. HG = 2 cm, HE = 2 cm, GC = 4 cm;C. HG = 4 cm, HE = 2 cm, GC = 2 cm;D. HG = 4 cm, HE = 4 cm, GC = 4 cm.
Phương pháp
Dựa vào tính chất các cạnh của hình hộp chữ nhật.
Lời giải
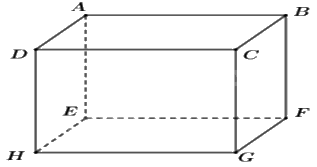
Hình hộp chữ nhật ABCD. EFGH có:
HG = AB = 4cm;
HE = BC = 2cm;
GC = AE = 4cm.
Đáp án A.
Câu 11: Tấm bìa bên dưới có thể tạo lập thành một hình lăng trụ đứng có đáy là tam giác đều.
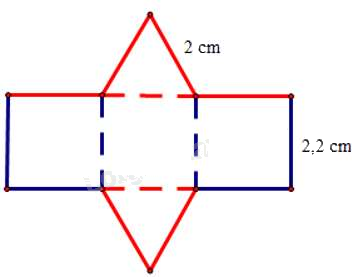
Chiều cao của hình lăng trụ đứng là:
A. 2 cm | B. 2,2 cm |
C. 4 cm | D. 4,4 cm |
Phương pháp
Quan sát hình vẽ.
Lời giải
Chiều cao của hình lăng trụ đứng là 2,2 cm.
Đáp án B.
Câu 12: Chọn phát biểu sai:A. Hai góc đối đỉnh thì bằng nhau;B. Hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia được gọi là hai gócđối đỉnh;C. Hai đường thẳng cắt nhau tại một điểm tạo thành hai cặp góc đối đỉnh;D. Hai góc bằng nhau thì đối đỉnh.
Phương pháp
Dựa vào kiến thức về hai góc đối đỉnh.
Lời giải
Hai góc bằng nhau chưa chắc đã là hai góc đối đỉnh nên đáp án D là đáp án sai.
Đáp án D.
Phần tự luận.
Bài 1: (1 điểm). Tìm x, biết
a. \(x - \frac{3}{4} = \frac{5}{{ - 7}}\) | b. 100 - \(\left| {x + 1} \right| = 90\) |
Phương pháp
Sử dụng quy tắc chuyển vế, kiến thức về giá trị tuyệt đối để giải tìm x.
Lời giải
a. \(x - \frac{3}{4} = \frac{5}{{ - 7}}\)
\(\begin{array}{l}x = \frac{5}{{ - 7}} + \frac{3}{4}\\x = \frac{1}{{28}}\end{array}\)
Vậy \(x = \frac{1}{{28}}\).
b. 100 - \(\left| {x + 1} \right| = 90\)
\(\begin{array}{l}|x + 1| = 100 - 90\\|x + 1| = 10\end{array}\)
=> x + 1 = 10 hoặc x + 1 = -10
hay x = 9 hoặc x = -11.
Vậy x = 9 hoặc x = -11.
Bài 2. (1,5 điểm). Thực hiện phép tính:
a) \(\frac{2}{3}:\frac{{ - 6}}{9} + \frac{1}{7}\); | b) \(\frac{{ - 3}}{{11}} \cdot \frac{5}{9} + \frac{4}{9} \cdot \frac{{ - 3}}{{11}}\); | c) \(\frac{{{9^5}{{.8}^2}}}{{{{27}^3}.16}}\). |
Phương pháp
Dựa vào quy tắc tính với số hữu tỉ và lũy thừa để tính.
Lời giải
a) \(\frac{2}{3}:\frac{{ - 6}}{9} + \frac{1}{7}\)
\( = \frac{2}{3}.\frac{{ - 9}}{6} + \frac{1}{7}\)\( = - 1 + \frac{1}{7}\)\( = \frac{{ - 6}}{7}\).
b) \(\frac{{ - 3}}{{11}} \cdot \frac{5}{9} + \frac{4}{9} \cdot \frac{{ - 3}}{{11}}\)
\( = \frac{{ - 3}}{{11}} \cdot \left( {\frac{5}{9} + \frac{4}{9}} \right)\)\( = \frac{{ - 3}}{{11}}.1\)\( = \frac{{ - 3}}{{11}}\).
c) \(\frac{{{9^5}{{.8}^2}}}{{{{27}^3}.16}}\)
\( = \frac{{{{\left( {{3^2}} \right)}^5}.{{\left( {{2^3}} \right)}^2}}}{{{{\left( {{3^3}} \right)}^3}{{.2}^4}}}\)\( = \frac{{{3^{10}}{{.2}^6}}}{{{3^9}{{.2}^4}}}\)\( = {3.2^2} = 3.4 = 12\)
Bài 3. (1 điểm) Bác Long có một căn phòng hình hộp chữ nhật có một cửa ra vào và mộtcửa sổ hình vuông với các kích thước như hình vẽ.
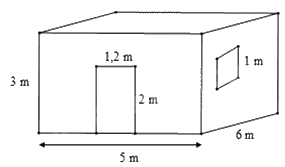
Hỏi bác Long cần trả bao nhiêu chi phí để sơn bốn bức tường xung quanh của căn phòng này(không sơn cửa)? Biết rằng để sơn mỗi mét vuông tốn 30 nghìn đồng.
Phương pháp
- Tính diện tích phần cần sơn:
Diện tích phần cần sơn = Diện tích xung quanh của căn phòng – Diện tích các cửa.
- Tính số tiền bác Long dùng để sơn căn phòng:
Số tiền dùng để sơn = diện tích phần cần sơn . chi phí sơn mỗi mét vuông.
Lời giải
Diện tích xung quanh của căn phòng là: Sxq = 2.(5 + 6).3 = 66(m2).Diện tích phần cửa lớn và cửa sổ là: 1,2 . 2 + 1 . 1 = 3,4 (m2).Diện tích phần cần sơn là: 66 – 3,4 = 62,6 (m2)Tổng chi phí cần để sơn là: 62,6. 30 000 = 1 878 000 (đồng).Vậy bác Long cần 1 878 000 đồng để sơn bốn bức tường xung quanh của căn phòng này.
Bài 4. (1,5 điểm) Một khối gỗ có dạng hình lăng trụ đứng đáy là tam giác vuông có kích thướcthước hai cạnh góc vuông là 3 dm; 4 dm, cạnh huyền (cạnh đối diện với góc vuông) là 0,5 m.Người ta khoét một lỗ lăng trụ đứng đáy tam giác vuông hai cạnh góc vuông có kích thước là1,5 dm; 2 dm; cạnh huyền 2,5 dm. Biết khối gỗ dài 0,45 m (hình vẽ).
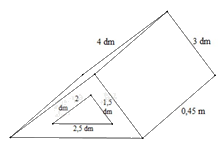
a) Tính thể tích của khối gỗ.b) Người ta muốn sơn tất cả các bề mặt của khối gỗ. Tính diện tích cần sơn (đơn vị mét vuông).
Phương pháp
a) Sử dụng công thức tính thể tích hình lăng trụ đứng.
b) Tính diện tích xung quanh khối kim loại, diện tích xung quanh lỗ, diện tích đáy.
Diện tích bề mặt cần sơn = diện tích xung quanh của khối gỗ + diện tích xung quanh của cái lỗ - diện tích hai đáy trừ đi diện tích hai cái đáy lỗ.
Lời giải
Đổi: 3 dm = 30 cm; 4 dm = 40 cm; 0,5 m = 50 cm;1,5 dm = 15 cm; 2 dm = 20 cm; 2,5 dm = 25 cm; 0,45 m = 45 cm.a) Thể tích khối gỗ là: \(\frac{1}{2}.40.30.45 - \frac{1}{2}.20.15.45{\rm{ }} = {\rm{ }}20250\)(cm3)b) Diện tích xung quanh của gỗ là: (30 + 40 + 50).45 = 5400(cm2)Diện tích xung quanh của cái lỗ là: (20 +15 + 25).45 = 2700(cm2)Diện tích hai đáy trừ đi diện tích hai cái đáy lỗ là:
\(\frac{1}{2}.30.40 - \frac{1}{2}.15.20 = 450\)(cm2)
Diện tích bề mặt cần sơn là: 5400 + 2700 - 450 = 7650(cm2) = 0,765(m2)Vậy diện tích cần sơn là 0,765m2.
Bài 5. (1,5 điểm) Cho hình vẽ dưới đây:
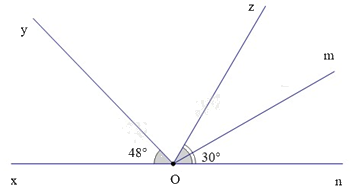Biết rằng \(\widehat {xOy} = {48^0},\widehat {mOn} = {30^0}\) và Om là phân giác của \(\widehat {zOn}\).a) Kể tên các góc (khác góc bẹt) kề với \(\widehat {zOm}\); góc kề bù với \(\widehat {mOn}\).b) Tính số đo của góc \(\widehat {yOz}\).
Phương pháp
a) Hai góc kề nhau là các góc có một cạnh chung và không có điểm trong chung; hai góc kề bù là hai góc kề nhau và có tổng bằng 1800.
b) \(\widehat {yOz} = 180 - \widehat {xOy} - \widehat {nOz}\).
Lời giải
a) Các góc (khác góc bẹt) kề với \(\widehat {zOm}\) là \(\widehat {zOy}\), \(\widehat {zOx}\), \(\widehat {mOn}\).Góc kề bù với \(\widehat {mOn}\) là \(\widehat {mOx}\).
b) Theo bài ta có Om là tia phân giác của \(\widehat {zOn}\).
Suy ra \(\widehat {zOm} = \widehat {mOn}\) (tính chất tia phân giác của một góc) (1)Mà \(\widehat {zOm} + \widehat {mOn} = \widehat {zOn}\) (hai góc kề nhau) (2)Từ (1) và (2) suy ra \(\widehat {zOm} = \widehat {mOn} = \frac{{\widehat {zOn}}}{2} \Rightarrow \widehat {zOn} = 2\widehat {mOn} = {2.30^0} = {60^0}\)Ta có \(\widehat {xOy} + \widehat {yOz} + \widehat {zOn} = \widehat {xOn} = {180^0}\)
Hay \({48^0} + \widehat {yOz} + {60^0} = {180^0} \Rightarrow \widehat {yOz} = {180^0} - {48^0} - {60^0} = {72^0}\)Vậy số đo của \(\widehat {yOz} = {72^0}\).
Bài 6. (0,5 điểm). Tìm hai số x, y. Tính giá trị nhỏ nhất của biểu thức: \({\rm{M}} = {({\rm{x}} - 5)^2} + 7\)
Phương pháp
Dựa vào đặc điểm của biểu thức (x – 5)2.
Lời giải
Ta có \({\left( {x - 5} \right)^2} \ge 0,\,\forall x \in \mathbb{R}\) nên \({\left( {x - 5} \right)^2} + 7 \ge 7,\,\forall x \in \mathbb{R}\) hay \(M \ge 7\). Dấu “=” xảy ra khi và chỉ khi \({\left( {x - 5} \right)^2} = 0 \Leftrightarrow x = 5\).
Vậy giá trị nhỏ nhất của M là 7 khi x = 5.
Kỳ thi giữa học kỳ 1 Toán 7 đóng vai trò quan trọng trong việc đánh giá năng lực học tập của học sinh sau một nửa học kỳ. Đề thi giữa kì 1 Toán 7 - Đề số 10 của giaitoan.edu.vn được xây dựng dựa trên cấu trúc đề thi thường gặp, bao gồm các chủ đề chính như số tự nhiên, số nguyên, phân số, tỉ lệ thức, và các bài toán đại số cơ bản.
Đề thi thường được chia thành các phần sau:
Dưới đây là một số dạng bài tập thường xuất hiện trong đề thi:
Ví dụ 1: Tính giá trị của biểu thức A = (1/2 + 1/3) * 6/5
Giải:
Ví dụ 2: Giải phương trình: x + 5 = 12
Giải:
Ngoài đề thi giữa kì 1 Toán 7 - Đề số 10, các em có thể tham khảo thêm các tài liệu sau:
Đề thi giữa kì 1 Toán 7 - Đề số 10 là một công cụ hữu ích giúp các em học sinh ôn tập và chuẩn bị tốt nhất cho kỳ thi sắp tới. Hãy luyện tập thường xuyên và áp dụng các kiến thức đã học để đạt kết quả tốt nhất!
