Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 1 Toán 7 - Đề số 11, một công cụ hữu ích giúp các em học sinh ôn luyện và đánh giá năng lực bản thân trước kỳ thi quan trọng. Đề thi được biên soạn theo chương trình học Toán 7, bao gồm các dạng bài tập thường gặp và có đáp án chi tiết đi kèm.
Với đề thi này, các em có thể tự tin làm bài và kiểm tra kiến thức đã học, đồng thời phát hiện những lỗ hổng để khắc phục kịp thời.
Kết quả phép tính \(0,5 + \frac{3}{{ - 4}}\) là
\(\frac{7}{4}\).
\(\frac{1}{4}\).
\(\frac{{ - 1}}{4}\).
\(\frac{{ - 19}}{8}\).
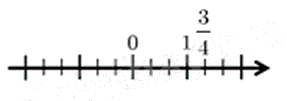
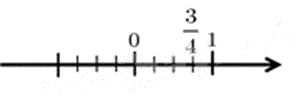
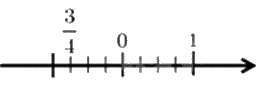
Cách biểu diễn số \(\frac{3}{4}\) trên trục số nào dưới đây đúng?

Tập hợp số hữu tỉ được kí hiệu là
\(\mathbb{N}\).
\(\mathbb{Z}\).
\({\mathbb{N}^*}\).
\(\mathbb{Q}\).
Giá trị của \({({2^3})^2}\) bằng
4.
8.
64.
16.
Trong các số hữu tỉ \(\frac{{ - 1}}{2};\frac{{ - 3}}{4};0;1;\frac{1}{2};\frac{4}{3}\) có bao nhiêu số hữu tỉ dương?
2.
3.
4.
5.
Điền kí hiệu thích hợp vào ô trống: \( - \frac{7}{6}{\rm{ }}...{\rm{ }}\mathbb{Q}\)
$\in $.
$\notin $.
$=$.
$<$.
Số nghịch đảo của số − 0,7 là
0,7.
\(\frac{{ - 7}}{{10}}\).
\( - \frac{{10}}{7}\).
\(\frac{{10}}{7}\).
Kết quả của phép tính \({\left( {\frac{{ - 3}}{4}} \right)^8}.{\left( {\frac{{ - 3}}{4}} \right)^2}\) là
\({\left( {\frac{{ - 3}}{4}} \right)^6}\).
\({\left( {\frac{{ - 3}}{4}} \right)^{10}}\).
\({\left( {\frac{{ - 3}}{4}} \right)^4}\).
\({\left( {\frac{{ - 3}}{4}} \right)^{16}}\).
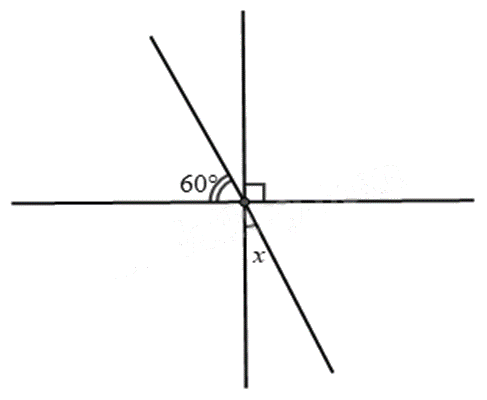
Tìm số đo \(x\) trong hình vẽ bên cạnh.
\(90^\circ \).
\(60^\circ \).
\(45^\circ \).
\(30^\circ \).
Hình lăng trụ đứng tam giác có số cạnh là
8.
12.
9.
10.
Hình nào sau đây là hình lăng trụ đứng tứ giác?
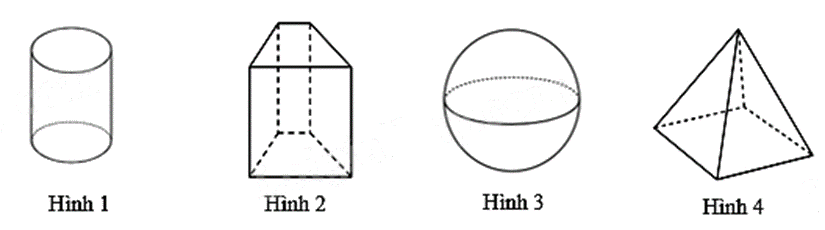
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Cho hình bên. Hãy chọn khẳng định đúng.
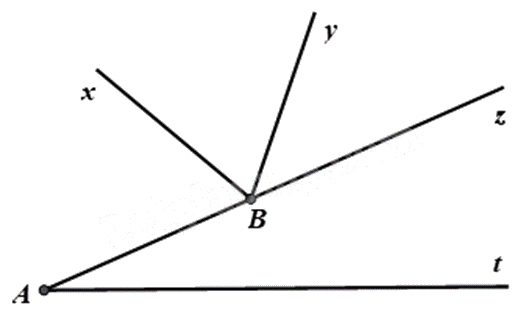
\(\widehat {xBy}\) và \(\widehat {yBz}\) là hai góc kề nhau.
\(\widehat {xBz}\) và \(\widehat {yBz}\) là hai góc kề bù.
\(\widehat {yBz}\) và \(\widehat {zAt}\) là hai góc kề nhau.
\(\widehat {ABy}\) và \(\widehat {xBz}\) là hai góc đối đỉnh.
Thực hiện phép tính
a) \(1\frac{2}{5} + 3\frac{3}{5}\)
b) \(\left( {\frac{{ - 5}}{9}} \right).\frac{3}{{11}} + \left( {\frac{{ - 4}}{9}} \right).\frac{3}{{11}}\)
c) \({\rm{2023 - }}{\left( {\frac{{\rm{1}}}{{\rm{3}}}} \right)^{\rm{2}}}{\rm{. }}{{\rm{3}}^{{\rm{ 2}}}}\)
d) \(\frac{{{5^{16}}{{.27}^7}}}{{{{125}^5}{{.9}^{11}}}}\)
Tìm x, biết:
a) \(x-\frac{{\rm{2}}}{{\rm{3}}}{\rm{ = }}\frac{{{\rm{ - 1}}}}{{\rm{3}}}\)
b) \(\frac{{\rm{7}}}{{\rm{3}}}.x + \frac{{\rm{4}}}{{\rm{7}}}{\rm{ = }}\frac{{{\rm{ - 3}}}}{{\rm{7}}}\)
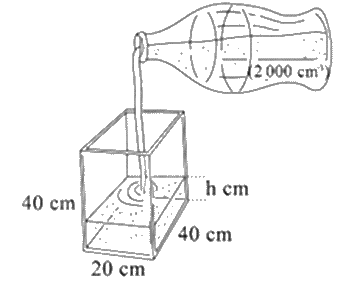
Một cái bể hình hộp chữ nhật và một cái chai có kích thước và thể tích như hình bên dưới. Cho biết một chai nước đầy rót hết vào bể có thể tích là \(2000c{m^3}\).
Tính chiều cao mực nước sau khi rót hết một chai nước vào bể.
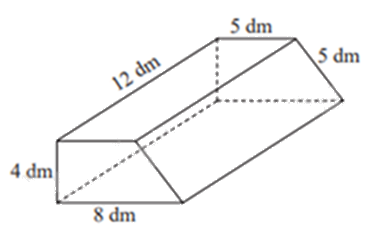
Một cái bục hình lăng trụ đứng tứ giác có kích thước như hình vẽ bên.
a) Tính diện tích xung quanh hình lăng trụ.
b) Người ta muốn sơn tất cả các mặt của cái bục trừ mặt nằm dưới đất. Hỏi chi phí để sơn là bao nhiêu? Biết rằng để sơn mỗi mét vuông tốn 25 nghìn đồng.
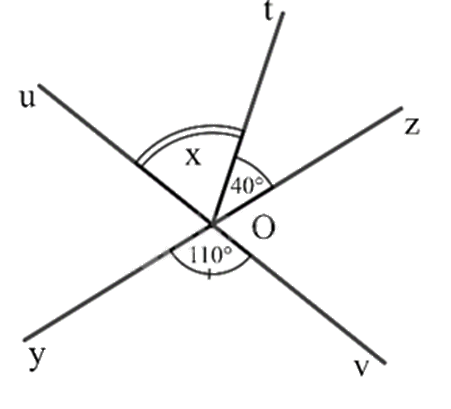
Quan sát hình vẽ
a) Góc đối đỉnh với \(\widehat {yOv}\) là góc nào?
b) Tìm số đo x của góc \(\widehat {uOt}\)?
Chào mừng năm học mới, Thế giới di dộng giảm giá một dòng máy tính bảng như sau: Đợt I giảm 10%, đợt II giảm 8% so với giá sau khi đã giảm ở đợt I. Chiếc máy tính bảng giá ban đầu là 20 000 000 đồng. Hỏi sau 2 đợt giảm giá chiếc máy tính bảng bán với giá bao nhiêu?
Kết quả phép tính \(0,5 + \frac{3}{{ - 4}}\) là
\(\frac{7}{4}\).
\(\frac{1}{4}\).
\(\frac{{ - 1}}{4}\).
\(\frac{{ - 19}}{8}\).
Đáp án : C
Đưa 0,5 về phân số, thực hiện phép cộng với hai số hữu tỉ.
Ta có: \(0,5 + \frac{3}{{ - 4}} = \frac{1}{2} + \frac{{ - 3}}{4} = \frac{2}{4} + \frac{{ - 3}}{4} = \frac{{ - 1}}{4}\).
Đáp án C.
Cách biểu diễn số \(\frac{3}{4}\) trên trục số nào dưới đây đúng?
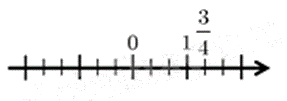
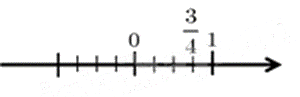
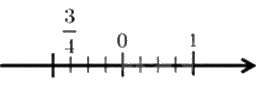

Đáp án : B
Dựa vào cách biểu diễn số hữu tỉ trên trục số.
Biểu diễn số hữu tỉ \(\frac{3}{4}\) trên trục số.
Chia đoạn thẳng đơn vị thành 4 phần bằng nhau. Lấy một đoạn làm đơn vị mới (đơn vị mới bằng \(\frac{1}{4}\) đơn vị cũ)
Số hữu tỉ được biểu diễn bằng điểm nằm bên phải gốc O, cách gốc O một đoạn bằng 3 đơn vị mới.
Do đó hình B biểu diễn số \(\frac{3}{4}\).

Đáp án B.
Tập hợp số hữu tỉ được kí hiệu là
\(\mathbb{N}\).
\(\mathbb{Z}\).
\({\mathbb{N}^*}\).
\(\mathbb{Q}\).
Đáp án : D
Dựa vào kí hiệu các tập hợp.
Tập hợp các số hữu tỉ được kí hiệu là \(\mathbb{Q}\).
Đáp án D.
Giá trị của \({({2^3})^2}\) bằng
4.
8.
64.
16.
Đáp án : C
Dựa vào kiến thức lũy thừa của lũy thừa: \({\left( {{a^m}} \right)^n} = {a^{m.n}}\).
Ta có: \({({2^3})^2} = {2^{3.2}} = {2^6} = 64\).
Đáp án C.
Trong các số hữu tỉ \(\frac{{ - 1}}{2};\frac{{ - 3}}{4};0;1;\frac{1}{2};\frac{4}{3}\) có bao nhiêu số hữu tỉ dương?
2.
3.
4.
5.
Đáp án : B
Số hữu tỉ dương là các số hữu tỉ lớn hơn 0.
Có 3 số hữu tỉ dương, đó là: \(1;\frac{1}{2};\frac{4}{3}\).
Đáp án B.
Điền kí hiệu thích hợp vào ô trống: \( - \frac{7}{6}{\rm{ }}...{\rm{ }}\mathbb{Q}\)
$\in $.
$\notin $.
$=$.
$<$.
Đáp án : A
Dựa vào kiến thức về các kí hiệu \( \in , \notin \).
Vì \( - \frac{7}{6}\) là số hữu tỉ nên \( - \frac{7}{6}{\rm{ }} \in {\rm{ }}\mathbb{Q}\).
Đáp án A.
Số nghịch đảo của số − 0,7 là
0,7.
\(\frac{{ - 7}}{{10}}\).
\( - \frac{{10}}{7}\).
\(\frac{{10}}{7}\).
Đáp án : C
Hai số được gọi là nghịch đảo nếu tích của chúng bằng 1.
Ta có: \( - 0,7 = - \frac{7}{{10}}\); \(\left( { - \frac{7}{{10}}} \right).\left( { - \frac{{10}}{7}} \right) = 1\) nên số nghịch đảo của \( - 0,7\) là \( - \frac{{10}}{7}\).
Đáp án C.
Kết quả của phép tính \({\left( {\frac{{ - 3}}{4}} \right)^8}.{\left( {\frac{{ - 3}}{4}} \right)^2}\) là
\({\left( {\frac{{ - 3}}{4}} \right)^6}\).
\({\left( {\frac{{ - 3}}{4}} \right)^{10}}\).
\({\left( {\frac{{ - 3}}{4}} \right)^4}\).
\({\left( {\frac{{ - 3}}{4}} \right)^{16}}\).
Đáp án : B
Sử dụng kiến thức tích hai lũy thừa cùng cơ số: \({a^m}.{a^n} = {a^{m + n}}\).
Ta có:
\({\left( {\frac{{ - 3}}{4}} \right)^8}.{\left( {\frac{{ - 3}}{4}} \right)^2} = {\left( {\frac{{ - 3}}{4}} \right)^{8 + 2}} = {\left( {\frac{{ - 3}}{4}} \right)^{10}}\).
Đáp án B.
Tìm số đo \(x\) trong hình vẽ bên cạnh.
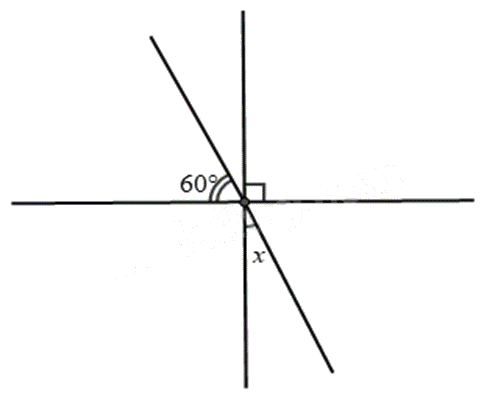
\(90^\circ \).
\(60^\circ \).
\(45^\circ \).
\(30^\circ \).
Đáp án : D
Dựa vào kiến thức về hai góc đối đỉnh và hai góc kề nhau.
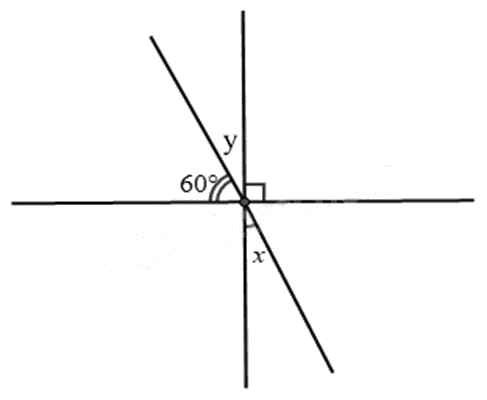
Ta đặt góc \(y\) như hình vẽ.
Vì \(y + 60^\circ = 90^\circ \) nên \(y = 90^\circ - 60^\circ = 30^\circ \).
Vì \(x\) và \(y\) là hai góc đối đỉnh nên \(x = y = 30^\circ \).
Đáp án D.
Hình lăng trụ đứng tam giác có số cạnh là
8.
12.
9.
10.
Đáp án : C
Dựa vào đặc điểm của hình lăng trụ đứng tam giác.
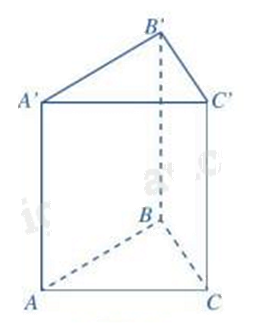
Hình lăng trụ đứng tam giác có 9 cạnh.
Đáp án C.
Hình nào sau đây là hình lăng trụ đứng tứ giác?
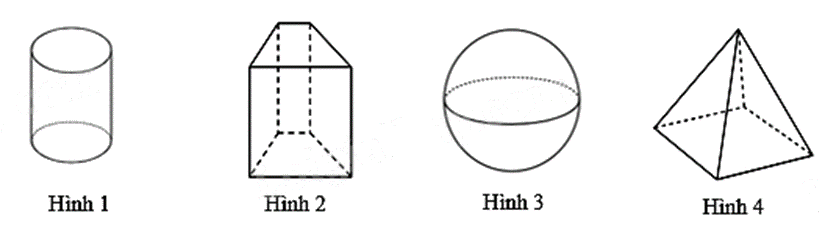
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Đáp án : B
Dựa vào kiến thức về hình lăng trụ đứng tứ giác.
Hình 2 là hình lăng trụ đứng tứ giác.
Đáp án B.
Cho hình bên. Hãy chọn khẳng định đúng.
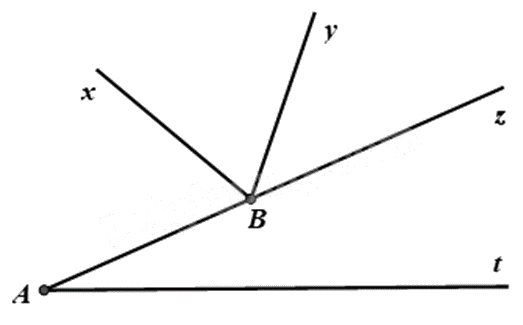
\(\widehat {xBy}\) và \(\widehat {yBz}\) là hai góc kề nhau.
\(\widehat {xBz}\) và \(\widehat {yBz}\) là hai góc kề bù.
\(\widehat {yBz}\) và \(\widehat {zAt}\) là hai góc kề nhau.
\(\widehat {ABy}\) và \(\widehat {xBz}\) là hai góc đối đỉnh.
Đáp án : A
Dựa vào kiến thức về hai góc kề nhau, hai góc kề bù, hai góc đối đỉnh.
\(\widehat {xBy}\) và \(\widehat {yBz}\) là hai góc kề nhau là khẳng định đúng.
\(\widehat {xBz}\) và \(\widehat {yBz}\) không phải là hai góc kề bù.
\(\widehat {yBz}\) và \(\widehat {zAt}\) không phải là hai góc kề nhau.
\(\widehat {ABy}\) và \(\widehat {xBz}\) không phải là hai góc đối đỉnh.
Đáp án A.
Thực hiện phép tính
a) \(1\frac{2}{5} + 3\frac{3}{5}\)
b) \(\left( {\frac{{ - 5}}{9}} \right).\frac{3}{{11}} + \left( {\frac{{ - 4}}{9}} \right).\frac{3}{{11}}\)
c) \({\rm{2023 - }}{\left( {\frac{{\rm{1}}}{{\rm{3}}}} \right)^{\rm{2}}}{\rm{. }}{{\rm{3}}^{{\rm{ 2}}}}\)
d) \(\frac{{{5^{16}}{{.27}^7}}}{{{{125}^5}{{.9}^{11}}}}\)
a) Đưa các hỗn số về phân số để thực hiện phép tính với số hữu tỉ.
b) Sử dụng tính chất phân phối của phép nhân đối với phép cộng.
c) Thực hiện phép tính với lũy thừa.
d) Thực hiện phép tính với lũy thừa.
a) \(1\frac{2}{5} + 3\frac{3}{5}\)
\(\begin{array}{l} = \frac{7}{5} + \frac{{18}}{5}\\ = \frac{{25}}{5} = 5\end{array}\)
b) \(\left( {\frac{{ - 5}}{9}} \right).\frac{3}{{11}} + \left( {\frac{{ - 4}}{9}} \right).\frac{3}{{11}}\)
\(\begin{array}{l} = \frac{3}{{11}}.\left[ {\left( {\frac{{ - 5}}{9}} \right) + \left( {\frac{{ - 4}}{9}} \right)} \right]\\ = \frac{3}{{11}}.\left( { - 1} \right) = \frac{{ - 3}}{{11}}\end{array}\)
c) \(2023 - {\left( {\frac{1}{3}} \right)^2}{.3^2}\)
\(\begin{array}{l} = 2023 - \frac{1}{9}.9\\ = 2023 - 1 = 2022\end{array}\)
d) \(\frac{{{5^{16}}{{.27}^7}}}{{{{125}^5}{{.9}^{11}}}}\)\( = \frac{{{5^{16}}.{{({3^3})}^7}}}{{{{({5^3})}^5}.{{({3^2})}^{11}}}}\)\( = \frac{{{5^{16}}{{.3}^{21}}}}{{{5^{15}}{{.3}^{22}}}}\)\( = \frac{5}{3}\)
Tìm x, biết:
a) \(x-\frac{{\rm{2}}}{{\rm{3}}}{\rm{ = }}\frac{{{\rm{ - 1}}}}{{\rm{3}}}\)
b) \(\frac{{\rm{7}}}{{\rm{3}}}.x + \frac{{\rm{4}}}{{\rm{7}}}{\rm{ = }}\frac{{{\rm{ - 3}}}}{{\rm{7}}}\)
Sử dụng quy tắc chuyển vế và thực hiện phép tính với số hữu tỉ để tìm x.
a) \(x - \frac{2}{3} = \frac{{ - 1}}{3}\)
\(\begin{array}{l}x = \left( {\frac{{ - 1}}{3}} \right) + \frac{2}{3}\\x = \frac{1}{3}\end{array}\)
Vậy \(x = \frac{1}{3}\).
b) \(\frac{7}{3}.x + \frac{4}{7} = \frac{{ - 3}}{7}\)
\(\begin{array}{l}\frac{7}{3}.x = \left( {\frac{{ - 3}}{7}} \right) - \frac{4}{7}\\\frac{7}{3}.x = - 1\\x = - 1:\frac{7}{3}\\x = - \frac{3}{7}\end{array}\)
Vậy \(x = - \frac{3}{7}\).
Một cái bể hình hộp chữ nhật và một cái chai có kích thước và thể tích như hình bên dưới. Cho biết một chai nước đầy rót hết vào bể có thể tích là \(2000c{m^3}\).
Tính chiều cao mực nước sau khi rót hết một chai nước vào bể.
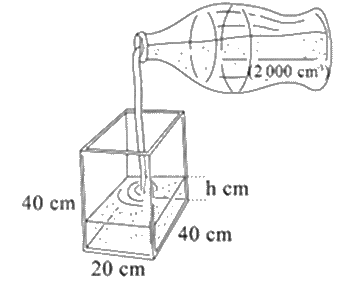
Dựa vào công thức tính thể tích của hình hộp chữ nhật suy ra chiều cao.
Vì \(V = h.S\) nên \(h = \frac{V}{S}\) (với V là thể tích; h là chiều cao, S là diện tích đáy).
Thể tích phần nước sau khi rót hết vào bể chính là thể tích của chai nước. Do đó thể tích phần nước trong bể là \(2000c{m^3}\).
Vì phần nước trong bể cũng là một hình hộp chữ nhật với kích thước đáy là kích thước bể nên thể tích phần nước trong bể là:
\(V = h.S\) hay \(2000 = h.20.40\)
Do đó chiều cao mực nước sau khi rót hết một chai nước vào bể là:
\(h = \frac{{2000}}{{20.40}} = 2,5\left( {cm} \right)\)
Vậy chiều cao mực nước sau khi rót hết một chai nước vào bể là \(2,5cm\).
Một cái bục hình lăng trụ đứng tứ giác có kích thước như hình vẽ bên.
a) Tính diện tích xung quanh hình lăng trụ.
b) Người ta muốn sơn tất cả các mặt của cái bục trừ mặt nằm dưới đất. Hỏi chi phí để sơn là bao nhiêu? Biết rằng để sơn mỗi mét vuông tốn 25 nghìn đồng.
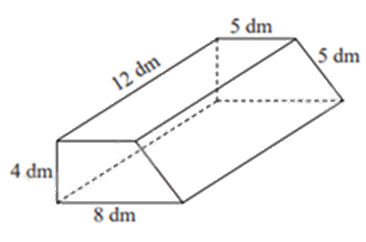
a) Sử dụng công thức tính diện tích xung quanh của hình lăng trụ: Sxq = Cđáy . h.
b) Tính diện tích hai đáy.
Tính diện tích cần sơn (gồm hai mặt đáy và 3 mặt bên (trừ mặt bên dưới)).
Chi phí bằng diện tích cần sơn . 25 nghìn đồng.
a) Diện tích xung quanh chiếc hộp là:
Sxq = Cđáy . h = (4 + 5 + 5 + 8) . 12 = 264 (dm2)
Diện tích 2 đáy là:
S2đáy = (5 + 8). 4 : 2 . 2 = 52 (dm2)
Các mặt cần sơn gồm hai mặt đáy và 3 mặt bên (trừ mặt bên dưới) nên diện tích phần cần sơn là:
264 + 52 – 8.12 = 220 (dm2) = 2,2 (m2)
Do đó chi phí để sơn là:
2,2 . 25 = 55 (nghìn đồng).
Quan sát hình vẽ
a) Góc đối đỉnh với \(\widehat {yOv}\) là góc nào?
b) Tìm số đo x của góc \(\widehat {uOt}\)?
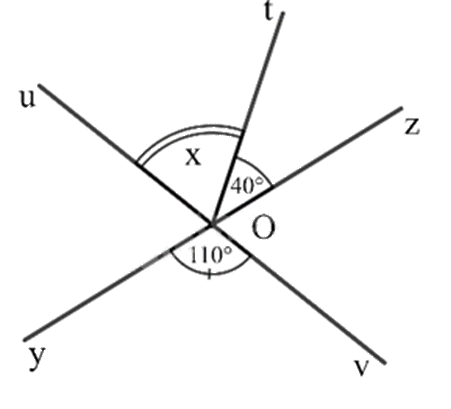
a) Dựa vào kiến thức về hai góc đối đỉnh.
b) Dựa vào kiến thức về hai góc đối đỉnh và hai góc kề nhau để tìm x.
a) Góc đối đỉnh với góc \(\widehat {yOv}\) là góc \(\widehat {uOz}\)
b) Vì hai góc \(\widehat {yOv}\) và \(\widehat {uOz}\) là hai góc đối đỉnh nên \(\widehat {yOv}{\rm{ = }}\widehat {uOz} = 110^\circ \)
Ta có: Vì \(\widehat {uOt}\) kề với \(\widehat {tOz}\) nên \(\widehat {uOt}{\rm{ + }}\widehat {tOz} = \widehat {uOz}\)
hay \(\widehat {uOt} + 40^\circ = 110^\circ \)
Suy ra \(\widehat {uOt} = 110^\circ - 40^\circ = 70^\circ \)
Chào mừng năm học mới, Thế giới di dộng giảm giá một dòng máy tính bảng như sau: Đợt I giảm 10%, đợt II giảm 8% so với giá sau khi đã giảm ở đợt I. Chiếc máy tính bảng giá ban đầu là 20 000 000 đồng. Hỏi sau 2 đợt giảm giá chiếc máy tính bảng bán với giá bao nhiêu?
Dựa vào đề bài để viết phép tính.
Giá của chiếc máy tính bảng sau 2 đợt giảm là
\(20000000.(100\% - 10\% ).(100\% - 8\% ) = 16560000\) (đồng)
Đề thi giữa kì 1 Toán 7 - Đề số 11 là một bài kiểm tra đánh giá kiến thức và kỹ năng giải toán của học sinh sau một nửa học kỳ đầu tiên của lớp 7. Đề thi thường bao gồm các chủ đề chính như số tự nhiên, số nguyên, phân số, tỉ lệ thức, và các bài toán đại số cơ bản. Cấu trúc đề thi có thể thay đổi tùy theo từng trường, nhưng thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh có sự chuẩn bị tốt nhất, chúng ta sẽ đi sâu vào phân tích nội dung chi tiết của Đề thi giữa kì 1 Toán 7 - Đề số 11. Dưới đây là một số dạng bài tập thường xuất hiện trong đề thi:
Các bài tập về số tự nhiên và số nguyên thường tập trung vào các kiến thức như:
Phân số là một trong những chủ đề quan trọng trong chương trình Toán 7. Các bài tập về phân số thường bao gồm:
Tỉ lệ thức là một khái niệm quan trọng trong chương trình Toán 7, giúp học sinh hiểu rõ hơn về mối quan hệ giữa các đại lượng. Các bài tập về tỉ lệ thức thường bao gồm:
Các bài toán đại số cơ bản thường yêu cầu học sinh vận dụng các kiến thức về biểu thức đại số, phương trình, và bất phương trình. Các dạng bài tập thường gặp bao gồm:
Để đạt kết quả tốt nhất trong kỳ thi giữa kì 1 Toán 7, các em học sinh cần có một kế hoạch ôn tập khoa học và hợp lý. Dưới đây là một số lời khuyên hữu ích:
Ngoài sách giáo khoa, các em học sinh có thể tham khảo thêm các tài liệu sau để ôn tập và nâng cao kiến thức:
Đề thi giữa kì 1 Toán 7 - Đề số 11 là một cơ hội tốt để các em học sinh đánh giá năng lực bản thân và chuẩn bị tốt nhất cho kỳ thi sắp tới. Hy vọng với những thông tin và lời khuyên trên, các em sẽ đạt được kết quả tốt nhất!