Chào mừng các em học sinh lớp 7 đến với đề thi giữa kì 1 Toán 7 - Đề số 3 của giaitoan.edu.vn. Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong giai đoạn giữa kì 1.
Đề thi bao gồm các dạng bài tập khác nhau, từ cơ bản đến nâng cao, giúp các em làm quen với nhiều dạng câu hỏi thường gặp trong các bài kiểm tra.
I. TRẮC NGHIỆM ( 3 điểm) Chọn chữ cái A,B,C hoặc D đứng trước câu trả lời đúng.
I. TRẮC NGHIỆM ( 3 điểm)
1.D | 2.B | 3.C | 4.B | 5.B | 6.C |
Câu 1:
Phương pháp:
Biểu diễn số hữu tỉ trên trục số.
Cách giải:
Để biểu diễn số hữu tỉ \(\dfrac{{ - 3}}{5}\) trên trục số, ta làm như sau:
- Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm 0 đến điểm 1) thành năm phần bằng nhau, lấy một đoạn làm đơn vị mới (đơn vị mới bằng \(\dfrac{1}{5}\) đơn vị cũ);
- Đi theo chiều âm của trục số, bắt đầu từ điểm 0, ta lấy 3 đơn vị mới đến điểm A. Điểm A biểu diễn số hữu tỉ \(\dfrac{{ - 3}}{5}\).

Chọn D.
Câu 2:
Phương pháp:
Thực hiện phép trừ số hữu tỉ
Cách giải:
Ta có: \( - 2,593 - \dfrac{2}{5}\)\( = - 2,593 - 0,4 = - \left( {2,593 + 0,4} \right) = - 2,993\)
Chọn B.
Câu 3:
Phương pháp:
Mỗi số thập phân vô hạn không tuần hoàn là biểu diễn thập phân của một số, số đó gọi là số vô tỉ.
Loại trừ từng đáp án, chỉ ra một số trong tập hợp không là số vô tỉ, từ đó tìm được đáp án đúng.
Cách giải:
+ Tâp hợp \(A = \left\{ { - 0,1;\sqrt {12} ;\dfrac{{21}}{{32}}; - 316} \right\}\)
Ta có: \( - 0,1\) là hữu tỉ nên tập hợp A không thỏa mãn.
+ Tập hợp \(B = \left\{ {32,1;\sqrt {25} ;\sqrt {\dfrac{1}{{16}}} ;\sqrt {0,01} } \right\}\)
Ta có: \(32,1\) là hữu tỉ nên tập hợp B không thỏa mãn.
+ Tập hợp \(\left\{ { - \dfrac{1}{2};\dfrac{{231}}{2};\dfrac{2}{5}; - 3} \right\}\)
Ta có: \( - \dfrac{1}{2}\) là hữu tỉ nên tập hợp D không thỏa mãn.
Chọn C.
Câu 4:
Phương pháp:
Diện tích xung quanh của hình hộp chữ nhật có ba kích thước: chiều dài là \(a\), chiều rộng là \(b\), chiều cao là \(c\) (\(a,b,c\) cùng đơn vị đo) được tính theo công thức: \({S_{xq}} = 2\left( {a + b} \right)c\)
Cách giải:
Diện tích xung quanh của hình hộp chữ nhật có ba kích thước: chiều dài là \(a\), chiều rộng là \(b\), chiều cao là \(c\) (\(a,b,c\) cùng đơn vị đo) được tính theo công thức: \({S_{xq}} = 2\left( {a + b} \right)c\)
Chọn B.
Câu 5:
Phương pháp:
Diện tích hình thang có hai đáy bé và đáy lớn lần lượt là \(a,b\) và chiều cao \(h\) được tính theo công thức \(S = \dfrac{{\left( {a + b} \right).h}}{2}\)
Thể tích hình lăng trụ có diện tích đáy là \(S\)đáy và chiều cao \(h\) được tính theo công thức \(V = S\)đáy \(.h\)
Cách giải:
Diện tích đáy của hình lăng trụ là: \(\dfrac{{\left( {4 + 8} \right).3}}{2} = 18\,\left( {c{m^2}} \right)\)
Thể tích của hình lăng trụ là: \(V = 18.9 = 162\,\left( {c{m^3}} \right)\)
Chọn B.
Câu 6:
Phương pháp:
Hai góc kề nhau là hai góc có một cạnh chung và không có điểm trong chung.
Cách giải:
4 góc kề với \(\angle AOC\) (không kể góc bẹt) trong hình vẽ là: \(\angle COM;\angle COB;\angle AON;\angle AOD\)
Chọn C.
Phần II. Tự luận
Bài 1:
Phương pháp:
Đưa các số về dạng phân số có cùng mẫu số dương để so sánh.
Cách giải:
a) Theo thứ tự tăng dần: \( - 3,7;\dfrac{{21}}{{11}};1\dfrac{1}{2};\dfrac{{ - 13}}{6};\dfrac{{ - 1}}{5};\dfrac{3}{7}\);
* So sánh các số: \( - 3,7;\dfrac{{ - 13}}{6};\dfrac{{ - 1}}{5}\)
Ta có: \(\, - 3,7 = \dfrac{{ - 37}}{{10}} = \dfrac{{ - 111}}{{30}};\dfrac{{ - 13}}{6} = \dfrac{{ - 65}}{{30}}\,\,;\,\dfrac{{ - 1}}{5} = \dfrac{{ - 6}}{{30}}\,\)
Vì \( - 111 < - 65 < - 6\) nên \(\dfrac{{ - 111}}{{30}} < \dfrac{{ - 65}}{{30}} < \dfrac{{ - 6}}{{30}}\) suy ra \( - 3,7 < \dfrac{{ - 13}}{6} < \dfrac{{ - 1}}{5}\) (1)
* So sánh các số: \(\dfrac{{21}}{{11}};1\dfrac{1}{2};\dfrac{3}{7}\)
Ta có: \(\dfrac{{21}}{{11}} = \dfrac{{294}}{{154}}\,;\,1\dfrac{1}{2} = \dfrac{3}{2} = \dfrac{{231}}{{154}}\,;\,\dfrac{3}{7} = \dfrac{{66}}{{154}}\)
Vì \(66 < 231 < 294\) nên \(\dfrac{{66}}{{254}} < \dfrac{{231}}{{154}} < \dfrac{{294}}{{154}}\) suy ra \(\dfrac{3}{7} < 1\dfrac{1}{2} < \dfrac{{21}}{{11}}\) (2)
Từ (1) và (2), suy ra \( - 3,7 < \dfrac{{ - 13}}{6} < \dfrac{{ - 1}}{5} < \dfrac{3}{7} < 1\dfrac{1}{2} < \dfrac{{21}}{{11}}\)
Vậy các số được sắp xếp theo thứ tự tăng dần là: \( - 3,7;\dfrac{{ - 13}}{6};\dfrac{{ - 1}}{5};\dfrac{3}{7};1\dfrac{1}{2};\dfrac{{21}}{{11}}.\)
b) Theo thứ tự giảm dần: \(\dfrac{{ - 3}}{{61}};0;\dfrac{{17}}{{48}};2\dfrac{1}{5};2,45;\dfrac{{ - 1}}{{10}}\).
* So sánh các số: \(\dfrac{{17}}{{48}};2\dfrac{1}{5};2,45\)
Ta có: \(\dfrac{{17}}{{48}} = \dfrac{{85}}{{240}};2\dfrac{1}{5} = \dfrac{{11}}{5} = \dfrac{{528}}{{240}};2,45 = \dfrac{{245}}{{100}} = \dfrac{{49}}{{20}} = \dfrac{{588}}{{240}}\)
Vì \(85 < 528 < 588\) nên \(\dfrac{{85}}{{240}} < \dfrac{{528}}{{240}} < \dfrac{{588}}{{240}}\) suy ra \(\dfrac{{17}}{{48}} < 2\dfrac{1}{5} < 2,45\) (1)
* So sánh các số: \(\dfrac{{ - 3}}{{61}};0;\dfrac{{ - 1}}{{10}}\)
Ta có: \(\dfrac{{ - 3}}{{61}} = \dfrac{{ - 30}}{{610}};0 = \dfrac{0}{{610}};\dfrac{{ - 1}}{{10}} = \dfrac{{ - 61}}{{610}}\)
Vì \( - 61 < - 30 < 0\) nên \(\dfrac{{ - 61}}{{610}} < \dfrac{{ - 30}}{{610}} < \dfrac{0}{{610}}\) nên \(\dfrac{{ - 1}}{{10}} < \dfrac{{ - 3}}{{61}} < 0\) (2)
Từ (1) và (2) suy ra \(\dfrac{{ - 1}}{{10}} < \dfrac{{ - 3}}{{61}} < 0 < \dfrac{{17}}{{48}} < 2\dfrac{1}{5} < 2,45\)
Vậy các số được sắp xếp theo thứ tự giảm dần là: \(2,45;2\dfrac{1}{5};\dfrac{{17}}{{48}};0;\dfrac{{ - 3}}{{61}};\dfrac{{ - 1}}{{10}}\).
Bài 2:
Phương pháp:
a, b: Vận dụng tính chất phân phối của phép cộng và phép nhân: \(a.\left( {b + d} \right) = a.b + a.d\)
c, d: Với hai số hữu tỉ \(x,y\), ta có: \({\left( {x.y} \right)^n} = {x^n}.{y^n};{\left( {\dfrac{x}{y}} \right)^n} = \dfrac{{{x^n}}}{{{y^n}}}\left( {y \ne 0} \right)\)
Cách giải:
a) \(\dfrac{{ - 5}}{6}.\dfrac{7}{{11}} + \dfrac{{ - 5}}{{11}}.\dfrac{4}{6} + \dfrac{5}{6}\)
\(\begin{array}{l} = \dfrac{5}{6}.\left( {\dfrac{{ - 7}}{{11}} + \dfrac{{ - 4}}{{11}} + 1} \right)\\ = \dfrac{5}{6}.\left( {\dfrac{{ - 11}}{{11}} + 1} \right)\\ = \dfrac{5}{6}.\left( { - 1 + 1} \right)\\ = \dfrac{5}{6}.0 = 0\end{array}\)
b) \(\left[ {\left( {\dfrac{{ - 3}}{8} + \dfrac{{11}}{{23}}} \right):\dfrac{5}{9} + \left( {\dfrac{{ - 5}}{8} + \dfrac{{12}}{{23}}} \right):\dfrac{5}{9}} \right].\dfrac{{ - 11}}{{325}}\)
\(\begin{array}{l} = \left[ {\left( {\dfrac{{ - 3}}{8} + \dfrac{{11}}{{23}}} \right).\dfrac{9}{5} + \left( {\dfrac{{ - 5}}{8} + \dfrac{{12}}{{23}}} \right).\dfrac{9}{5}} \right].\dfrac{{ - 11}}{{325}}\\ = \left[ {\dfrac{9}{5}.\left( {\dfrac{{ - 3}}{8} + \dfrac{{11}}{{23}} + \dfrac{{ - 5}}{8} + \dfrac{{12}}{{23}}} \right)} \right].\dfrac{{ - 11}}{{325}}\\ = \left[ {\dfrac{9}{5}.\left( {\dfrac{{ - 8}}{8} + \dfrac{{23}}{{23}}} \right)} \right].\dfrac{{ - 11}}{{325}}\\ = \dfrac{9}{5}.\left( { - 1 + 1} \right).\dfrac{{ - 11}}{{325}}\\ = \dfrac{9}{5}.0.\dfrac{{ - 11}}{{325}}\\ = 0\end{array}\)
c) \(\dfrac{{{{15}^5}}}{{{5^5}}} - {\left( { - 0,25} \right)^2}{.4^2}\)
\(\begin{array}{l} = {\left( {\dfrac{{15}}{5}} \right)^5} - {\left( { - 0,25.4} \right)^2}\\ = {3^5} - {\left( { - 1} \right)^2}\\ = 243 - 1\\ = 242\end{array}\)
d) \( - \dfrac{{{2^{15}}{{.9}^4}}}{{{6^6}{{.8}^3}}} + 0,75.\dfrac{{ - 1}}{2} + 0,375\)
\(\begin{array}{l} = - \dfrac{{{2^{15}}.{{\left( {{3^2}} \right)}^4}}}{{{{\left( {2.3} \right)}^6}.{{\left( {{2^3}} \right)}^3}}} + \left( { - 0,375} \right) + 0,375\\ = - \dfrac{{{2^{15}}{{.3}^8}}}{{{2^6}{{.3}^6}{{.2}^9}}} + \left[ {\left( { - 0,375} \right) + 0,375} \right]\\ = - \dfrac{{{2^{15}}{{.3}^8}}}{{{2^{15}}{{.3}^6}}} + 0\\ = - {3^2} = 9\end{array}\)
Bài 3:
Phương pháp:
Vận dụng quy tắc chuyển vế để tìm \(x\).
Cách giải:
a) \(\left( { - 0,4} \right).\left( {2x + \dfrac{2}{5}} \right) = - 9,4\)
\(\begin{array}{l}2x + \dfrac{2}{5} = - 9,4:\left( { - 0,4} \right)\\2x + \dfrac{2}{5} = \dfrac{{ - 94}}{{10}}:\dfrac{{\left( { - 4} \right)}}{{10}}\\2x + \dfrac{2}{5} = \dfrac{{ - 94}}{{10}}.\dfrac{{10}}{{\left( { - 4} \right)}}\\2x + \dfrac{2}{5} = \dfrac{{47}}{2}\\2x = \dfrac{{47}}{2} - \dfrac{2}{5}\end{array}\)
\(\begin{array}{l}2x = \dfrac{{235}}{{10}} - \dfrac{4}{{10}}\\2x = \dfrac{{231}}{{10}}\\x = \dfrac{{231}}{{10}}:2\\x = \dfrac{{231}}{{20}}\end{array}\)
Vậy \(x = \dfrac{{231}}{{20}}\)
b) \(\left( {\dfrac{3}{2} - x} \right):\dfrac{{ - 14}}{3} = - \dfrac{6}{7}\)
\(\begin{array}{l}\dfrac{3}{2} - x = \dfrac{{ - 6}}{7}.\dfrac{{\left( { - 14} \right)}}{3}\\\dfrac{3}{2} - x = 4\\x = \dfrac{3}{2} - 4\\x = \dfrac{3}{2} - \dfrac{8}{2}\\x = \dfrac{{ - 5}}{2}\end{array}\)
Vậy \(x = \dfrac{{ - 5}}{2}\)
c) \(x + 2.\sqrt {16} = - 3.\sqrt {49} \)
\(\begin{array}{l}x + 2.\sqrt {{4^2}} = - 2\sqrt {{7^2}} \\x + 2.4 = - 2.7\\x + 8 = - 14\\x = - 14 - 8\\x = - 22\end{array}\)
Vậy \(x = - 22\)
d) \(2 + \dfrac{1}{6} - x = 10.\sqrt {0,01} - \sqrt {\dfrac{{25}}{{36}}} \)
\(\begin{array}{l}\dfrac{{12}}{6} + \dfrac{1}{6} - x = 10.\sqrt {{{\left( {0,1} \right)}^2}} - \sqrt {\dfrac{{{5^2}}}{{{6^2}}}} \\\dfrac{{13}}{6} - x = 10.0,1 - \dfrac{5}{6}\\\dfrac{{13}}{6} - x = 1 - \dfrac{5}{6} = \dfrac{6}{6} - \dfrac{5}{6}\\\dfrac{{13}}{6} - x = \dfrac{1}{6}\\x = \dfrac{{13}}{6} - \dfrac{1}{6}\\x = \dfrac{{12}}{6}\\x = 2\end{array}\)
Vậy \(x = 2\)
Bài 4:
Phương pháp:
Diện tích xung quanh của căn phòng theo công thức tính diên tích xung quanh của hình hộp chữ nhật có ba kích thước: chiều dài là \(a\), chiều rộng là \(b\), chiều cao là \(c\) (\(a,b,c\) cùng đơn vị đo) được tính theo công thức: \({S_{xq}} = 2\left( {a + b} \right)c\)(1)
Diện tích trần của căn phòng được tính theo công thức diện tích hình chữ nhật có chiều rộng là \(a\), chiều dài là \(b\) thì \(S = ab\) (2)
Diện tích cần quét sơn = (1) + (2) – diện tích các của sổ
Số tiền phải chi trả = diện tích cần quét sơn . giá tiền \(1{m^2}\)
Cách giải:
Diện tích xung quanh của căn phòng là:
\(2.\left( {6 + 4,2} \right).3,2 = 65,28\,\left( {{m^2}} \right)\)
Diện tích trần của căn phòng là:
\(6.4,2 = 25,2\,\left( {{m^2}} \right)\)
Diện tích cần quét sơn của căn phòng là:
\(65,28 + 25,2 - 8,48 = 82\,\left( {{m^2}} \right)\)
Số tiền người đó cần phải trả để quét sơn căn phòng là:
\(82.12\,100 = 992\,200\) (đồng)
Bài 5:
Phương pháp:
Vận dụng kiến thức tia phân giác của một góc; hai góc kề nhau.
Cách giải:

a) Vì \(OG\) là tia phân giác của \(\angle COD\) nên \(\angle COG = \angle DOG = \dfrac{1}{2}\angle COD = \dfrac{1}{2}{.80^0} = {40^0}\) (tính chất tia phân giác của một góc)
Vì hai góc \(\angle COG\) và \(\angle EOG\) là hai góc kề nhau nên \(\angle COG + \angle EOG = \angle COE\)
Suy ra \({40^0} + \angle EOG = {60^0}\)
\( \Rightarrow \angle EOG = {60^0} - {40^0} = {20^0}\)
Vậy \(\angle EOG = {20^0}\)
b) Vì hai góc \(\angle COE\) và \(\angle DOE\) là hai góc kề nhau nên \(\angle COE + \angle DOE = \angle COD\)
Suy ra \({60^0} + \angle DOE = {80^0}\)
\( \Rightarrow \angle DOE = {80^0} - {60^0} = {20^0}\)
Do đó, \(\angle EOG = \angle DOE = {20^0}\)
Mặt khác \(OE\) nằm giữa hai tia \(OD\) và \(OG\) nên \(OE\) là tia phân giác của \(\angle DOG\).
I. TRẮC NGHIỆM ( 3 điểm)
Chọn chữ cái A,B,C hoặc D đứng trước câu trả lời đúng.
Câu 1: Điểm biểu diễn của số hữu tỉ \(\dfrac{{ - 3}}{5}\) trên trục số là hình vẽ nào dưới đây?
A. 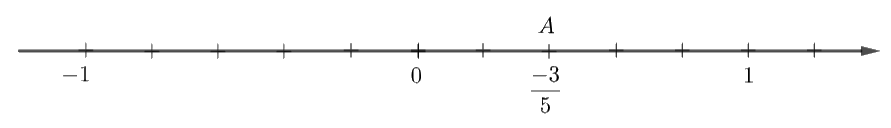
B. 
C. 
D.
Câu 2: Kết quả của phép tính: \( - 2,593 - \dfrac{2}{5}\) là:
A. \(2,993\)
B. \( - 2,993\)
C. \(2,193\)
D. \( - 2,193\)
Câu 3: Trong các tập hợp sau, tập hợp nào có tất cả các phần tử đều là số vô tỉ?
A. \(A = \left\{ { - 0,1;\sqrt {12} ;\dfrac{{21}}{{32}}; - 316} \right\}\)
B. \(B = \left\{ {32,1;\sqrt {25} ;\sqrt {\dfrac{1}{{16}}} ;\sqrt {0,01} } \right\}\)
C. \(C = \left\{ {\sqrt 3 ;\sqrt 5 ;\sqrt {31} ;\sqrt {83} } \right\}\)
D. \(D = \left\{ { - \dfrac{1}{2};\dfrac{{231}}{2};\dfrac{2}{5}; - 3} \right\}\)
Câu 4: Hình hộp chữ nhật có ba kích thước: chiều dài là \(a\), chiều rộng là \(b\), chiều cao là \(c\) (\(a,b,c\) cùng đơn vị đo). Khi đó, diện tích xung quanh của hình hộp chữ nhật được tính theo công thức:
A. \({S_{xq}} = \left( {a + b} \right)c\)
B. \({S_{xq}} = 2\left( {a + b} \right)c\)
C. \({S_{xq}} = \left( {b + c} \right)a\)
D. \({S_{xq}} = 2\left( {b + c} \right)a\)
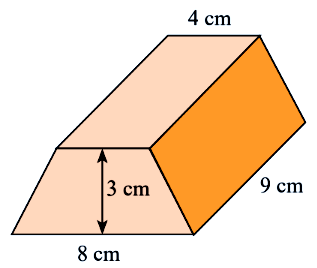
Câu 5: Tính thể tích hình lăng trụ đứng có đáy là hình thang cân có kích thước như hình bên dưới:
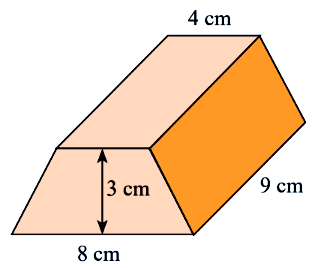
A. \(72c{m^3}\)
B. \(162c{m^3}\)
C. \(88c{m^3}\)
D. \(132c{m^3}\)
Câu 6: Hãy kể tên 4 góc kề với \(\angle AOC\) (không kể góc bẹt) trong hình vẽ dưới đây:
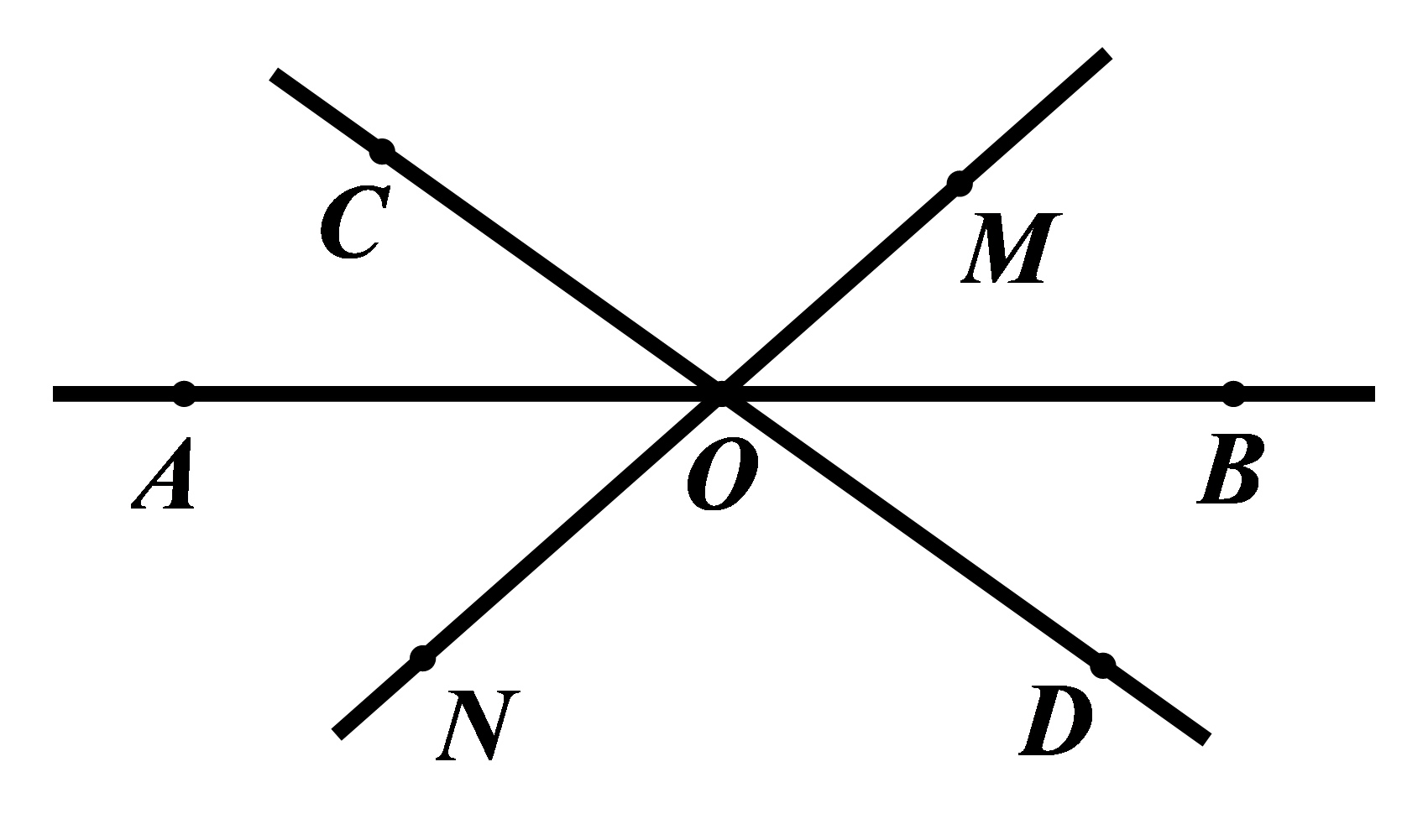
A. \(\angle COM;\angle MOB;\angle AON;\angle DOB\)
B. \(\angle COM;\angle COD;\angle AON;\angle MON\)
C. \(\angle COM;\angle COB;\angle AON;\angle AOD\)
D. \(\angle COM;\angle MOD;\angle AON;\angle CON\)
Phần II. Tự luận (7 điểm):
Bài 1: (1 điểm)
Sắp xếp các số sau:
a) Theo thứ tự tăng dần: \( - 3,7;\dfrac{{21}}{{11}};1\dfrac{1}{2};\dfrac{{ - 13}}{6};\dfrac{{ - 1}}{5};\dfrac{3}{7}\);
b) Theo thứ tự giảm dần: \(\dfrac{{ - 3}}{{61}};0;\dfrac{{17}}{{48}};2\dfrac{1}{5};2,45;\dfrac{{ - 1}}{{10}}\).
Bài 2: (2,0 điểm)
Tính một cách hợp lí:
a) \(\dfrac{{ - 5}}{6}.\dfrac{7}{{11}} + \dfrac{{ - 5}}{{11}}.\dfrac{4}{6} + \dfrac{5}{6}\)
b) \(\left[ {\left( {\dfrac{{ - 3}}{8} + \dfrac{{11}}{{23}}} \right):\dfrac{5}{9} + \left( {\dfrac{{ - 5}}{8} + \dfrac{{12}}{{23}}} \right):\dfrac{5}{9}} \right].\dfrac{{ - 11}}{{325}}\)
c) \(\dfrac{{{{15}^5}}}{{{5^5}}} - {\left( { - 0,25} \right)^2}{.4^2}\)
d) \( - \dfrac{{{2^{15}}{{.9}^4}}}{{{6^6}{{.8}^3}}} + 0,75.\dfrac{{ - 1}}{2} + 0,375\)
Bài 3: (2,0 điểm)
Tìm \(x\), biết:
a) \(\left( { - 0,4} \right).\left( {2x + \dfrac{2}{5}} \right) = - 9,4\)
b) \(\left( {\dfrac{3}{2} - x} \right):\dfrac{{ - 14}}{3} = - \dfrac{6}{7}\)
c) \(x + 2.\sqrt {16} = - 3.\sqrt {49} \)
d) \(2 + \dfrac{1}{6} - x = 10.\sqrt {0,01} - \sqrt {\dfrac{{25}}{{36}}} \)
Bài 4: (1,0 điểm)
Một căn phòng có dạng hình hộp chữ nhật với chiều dài là 6m, chiều rộng là 4,2m, chiều cao là 3,2m. Người ta muốn sơn phía trong bốn bức tường và cả trần của căn phòng. Tính số tiền mà người ta phải trả, biết diện tích của các của của căn phòng là và giá tiền mỗi mét vuông (bao gồm tiền công và nguyên vật liệu) là 12 100 đồng.
Bài 5: (1,0 điểm)
Quan sát hình vẽ bên dưới, có \(\angle COD = {80^0};\angle COE = {60^0}\), tia \(OG\) là tia phân giác của\(\angle COD\).

a) Tính số đo của \(\angle EOG?\)
b) Tia \(OE\) có là tia phân giác của \(\angle DOG\) hay không? Giải thích vì sao?
I. TRẮC NGHIỆM ( 3 điểm)
Chọn chữ cái A,B,C hoặc D đứng trước câu trả lời đúng.
Câu 1: Điểm biểu diễn của số hữu tỉ \(\dfrac{{ - 3}}{5}\) trên trục số là hình vẽ nào dưới đây?
A. 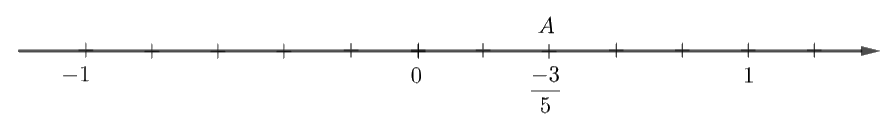
B. 
C. 
D.
Câu 2: Kết quả của phép tính: \( - 2,593 - \dfrac{2}{5}\) là:
A. \(2,993\)
B. \( - 2,993\)
C. \(2,193\)
D. \( - 2,193\)
Câu 3: Trong các tập hợp sau, tập hợp nào có tất cả các phần tử đều là số vô tỉ?
A. \(A = \left\{ { - 0,1;\sqrt {12} ;\dfrac{{21}}{{32}}; - 316} \right\}\)
B. \(B = \left\{ {32,1;\sqrt {25} ;\sqrt {\dfrac{1}{{16}}} ;\sqrt {0,01} } \right\}\)
C. \(C = \left\{ {\sqrt 3 ;\sqrt 5 ;\sqrt {31} ;\sqrt {83} } \right\}\)
D. \(D = \left\{ { - \dfrac{1}{2};\dfrac{{231}}{2};\dfrac{2}{5}; - 3} \right\}\)
Câu 4: Hình hộp chữ nhật có ba kích thước: chiều dài là \(a\), chiều rộng là \(b\), chiều cao là \(c\) (\(a,b,c\) cùng đơn vị đo). Khi đó, diện tích xung quanh của hình hộp chữ nhật được tính theo công thức:
A. \({S_{xq}} = \left( {a + b} \right)c\)
B. \({S_{xq}} = 2\left( {a + b} \right)c\)
C. \({S_{xq}} = \left( {b + c} \right)a\)
D. \({S_{xq}} = 2\left( {b + c} \right)a\)
Câu 5: Tính thể tích hình lăng trụ đứng có đáy là hình thang cân có kích thước như hình bên dưới:
A. \(72c{m^3}\)
B. \(162c{m^3}\)
C. \(88c{m^3}\)
D. \(132c{m^3}\)
Câu 6: Hãy kể tên 4 góc kề với \(\angle AOC\) (không kể góc bẹt) trong hình vẽ dưới đây:
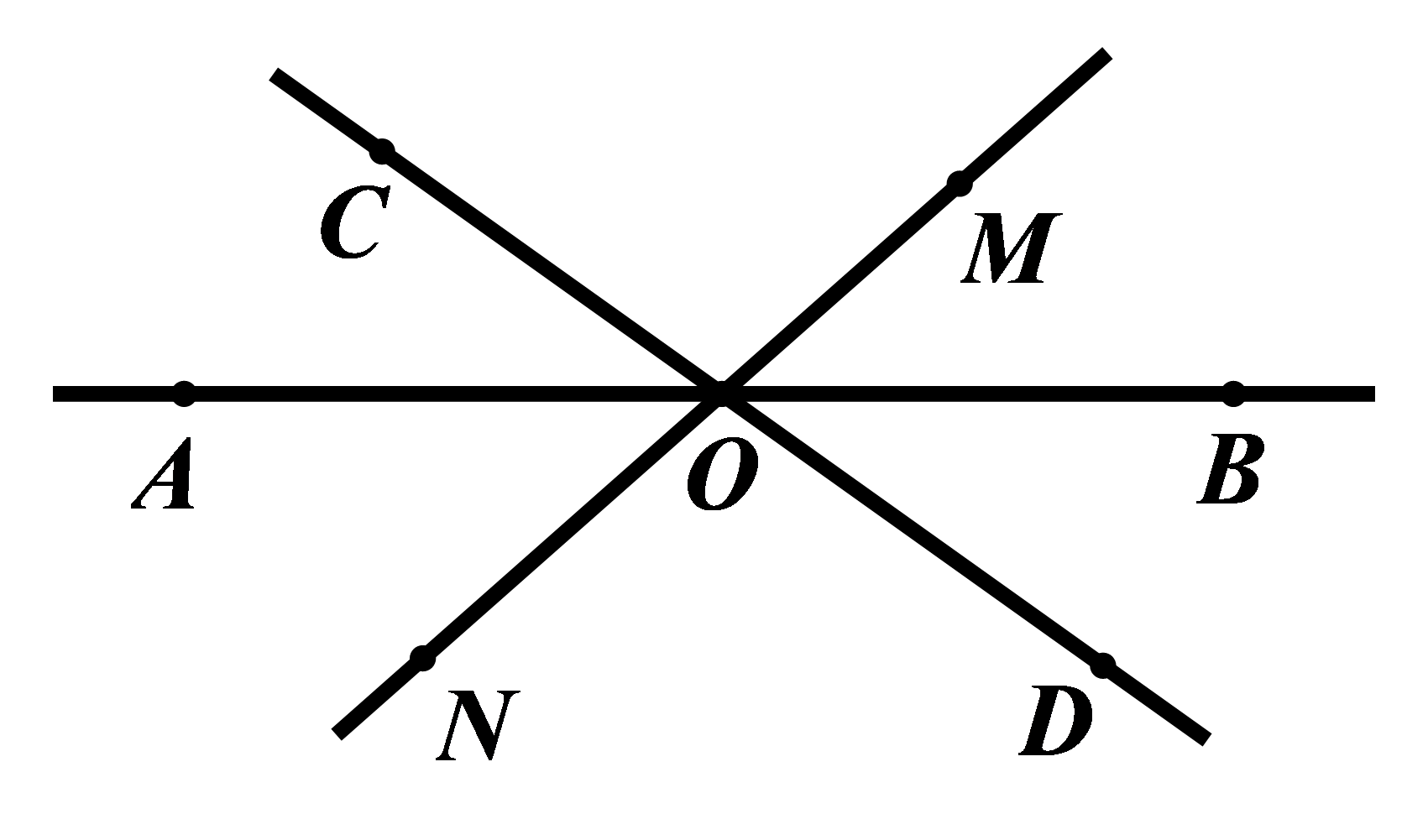
A. \(\angle COM;\angle MOB;\angle AON;\angle DOB\)
B. \(\angle COM;\angle COD;\angle AON;\angle MON\)
C. \(\angle COM;\angle COB;\angle AON;\angle AOD\)
D. \(\angle COM;\angle MOD;\angle AON;\angle CON\)
Phần II. Tự luận (7 điểm):
Bài 1: (1 điểm)
Sắp xếp các số sau:
a) Theo thứ tự tăng dần: \( - 3,7;\dfrac{{21}}{{11}};1\dfrac{1}{2};\dfrac{{ - 13}}{6};\dfrac{{ - 1}}{5};\dfrac{3}{7}\);
b) Theo thứ tự giảm dần: \(\dfrac{{ - 3}}{{61}};0;\dfrac{{17}}{{48}};2\dfrac{1}{5};2,45;\dfrac{{ - 1}}{{10}}\).
Bài 2: (2,0 điểm)
Tính một cách hợp lí:
a) \(\dfrac{{ - 5}}{6}.\dfrac{7}{{11}} + \dfrac{{ - 5}}{{11}}.\dfrac{4}{6} + \dfrac{5}{6}\)
b) \(\left[ {\left( {\dfrac{{ - 3}}{8} + \dfrac{{11}}{{23}}} \right):\dfrac{5}{9} + \left( {\dfrac{{ - 5}}{8} + \dfrac{{12}}{{23}}} \right):\dfrac{5}{9}} \right].\dfrac{{ - 11}}{{325}}\)
c) \(\dfrac{{{{15}^5}}}{{{5^5}}} - {\left( { - 0,25} \right)^2}{.4^2}\)
d) \( - \dfrac{{{2^{15}}{{.9}^4}}}{{{6^6}{{.8}^3}}} + 0,75.\dfrac{{ - 1}}{2} + 0,375\)
Bài 3: (2,0 điểm)
Tìm \(x\), biết:
a) \(\left( { - 0,4} \right).\left( {2x + \dfrac{2}{5}} \right) = - 9,4\)
b) \(\left( {\dfrac{3}{2} - x} \right):\dfrac{{ - 14}}{3} = - \dfrac{6}{7}\)
c) \(x + 2.\sqrt {16} = - 3.\sqrt {49} \)
d) \(2 + \dfrac{1}{6} - x = 10.\sqrt {0,01} - \sqrt {\dfrac{{25}}{{36}}} \)
Bài 4: (1,0 điểm)
Một căn phòng có dạng hình hộp chữ nhật với chiều dài là 6m, chiều rộng là 4,2m, chiều cao là 3,2m. Người ta muốn sơn phía trong bốn bức tường và cả trần của căn phòng. Tính số tiền mà người ta phải trả, biết diện tích của các của của căn phòng là và giá tiền mỗi mét vuông (bao gồm tiền công và nguyên vật liệu) là 12 100 đồng.
Bài 5: (1,0 điểm)
Quan sát hình vẽ bên dưới, có \(\angle COD = {80^0};\angle COE = {60^0}\), tia \(OG\) là tia phân giác của\(\angle COD\).

a) Tính số đo của \(\angle EOG?\)
b) Tia \(OE\) có là tia phân giác của \(\angle DOG\) hay không? Giải thích vì sao?
I. TRẮC NGHIỆM ( 3 điểm)
1.D | 2.B | 3.C | 4.B | 5.B | 6.C |
Câu 1:
Phương pháp:
Biểu diễn số hữu tỉ trên trục số.
Cách giải:
Để biểu diễn số hữu tỉ \(\dfrac{{ - 3}}{5}\) trên trục số, ta làm như sau:
- Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm 0 đến điểm 1) thành năm phần bằng nhau, lấy một đoạn làm đơn vị mới (đơn vị mới bằng \(\dfrac{1}{5}\) đơn vị cũ);
- Đi theo chiều âm của trục số, bắt đầu từ điểm 0, ta lấy 3 đơn vị mới đến điểm A. Điểm A biểu diễn số hữu tỉ \(\dfrac{{ - 3}}{5}\).

Chọn D.
Câu 2:
Phương pháp:
Thực hiện phép trừ số hữu tỉ
Cách giải:
Ta có: \( - 2,593 - \dfrac{2}{5}\)\( = - 2,593 - 0,4 = - \left( {2,593 + 0,4} \right) = - 2,993\)
Chọn B.
Câu 3:
Phương pháp:
Mỗi số thập phân vô hạn không tuần hoàn là biểu diễn thập phân của một số, số đó gọi là số vô tỉ.
Loại trừ từng đáp án, chỉ ra một số trong tập hợp không là số vô tỉ, từ đó tìm được đáp án đúng.
Cách giải:
+ Tâp hợp \(A = \left\{ { - 0,1;\sqrt {12} ;\dfrac{{21}}{{32}}; - 316} \right\}\)
Ta có: \( - 0,1\) là hữu tỉ nên tập hợp A không thỏa mãn.
+ Tập hợp \(B = \left\{ {32,1;\sqrt {25} ;\sqrt {\dfrac{1}{{16}}} ;\sqrt {0,01} } \right\}\)
Ta có: \(32,1\) là hữu tỉ nên tập hợp B không thỏa mãn.
+ Tập hợp \(\left\{ { - \dfrac{1}{2};\dfrac{{231}}{2};\dfrac{2}{5}; - 3} \right\}\)
Ta có: \( - \dfrac{1}{2}\) là hữu tỉ nên tập hợp D không thỏa mãn.
Chọn C.
Câu 4:
Phương pháp:
Diện tích xung quanh của hình hộp chữ nhật có ba kích thước: chiều dài là \(a\), chiều rộng là \(b\), chiều cao là \(c\) (\(a,b,c\) cùng đơn vị đo) được tính theo công thức: \({S_{xq}} = 2\left( {a + b} \right)c\)
Cách giải:
Diện tích xung quanh của hình hộp chữ nhật có ba kích thước: chiều dài là \(a\), chiều rộng là \(b\), chiều cao là \(c\) (\(a,b,c\) cùng đơn vị đo) được tính theo công thức: \({S_{xq}} = 2\left( {a + b} \right)c\)
Chọn B.
Câu 5:
Phương pháp:
Diện tích hình thang có hai đáy bé và đáy lớn lần lượt là \(a,b\) và chiều cao \(h\) được tính theo công thức \(S = \dfrac{{\left( {a + b} \right).h}}{2}\)
Thể tích hình lăng trụ có diện tích đáy là \(S\)đáy và chiều cao \(h\) được tính theo công thức \(V = S\)đáy \(.h\)
Cách giải:
Diện tích đáy của hình lăng trụ là: \(\dfrac{{\left( {4 + 8} \right).3}}{2} = 18\,\left( {c{m^2}} \right)\)
Thể tích của hình lăng trụ là: \(V = 18.9 = 162\,\left( {c{m^3}} \right)\)
Chọn B.
Câu 6:
Phương pháp:
Hai góc kề nhau là hai góc có một cạnh chung và không có điểm trong chung.
Cách giải:
4 góc kề với \(\angle AOC\) (không kể góc bẹt) trong hình vẽ là: \(\angle COM;\angle COB;\angle AON;\angle AOD\)
Chọn C.
Phần II. Tự luận
Bài 1:
Phương pháp:
Đưa các số về dạng phân số có cùng mẫu số dương để so sánh.
Cách giải:
a) Theo thứ tự tăng dần: \( - 3,7;\dfrac{{21}}{{11}};1\dfrac{1}{2};\dfrac{{ - 13}}{6};\dfrac{{ - 1}}{5};\dfrac{3}{7}\);
* So sánh các số: \( - 3,7;\dfrac{{ - 13}}{6};\dfrac{{ - 1}}{5}\)
Ta có: \(\, - 3,7 = \dfrac{{ - 37}}{{10}} = \dfrac{{ - 111}}{{30}};\dfrac{{ - 13}}{6} = \dfrac{{ - 65}}{{30}}\,\,;\,\dfrac{{ - 1}}{5} = \dfrac{{ - 6}}{{30}}\,\)
Vì \( - 111 < - 65 < - 6\) nên \(\dfrac{{ - 111}}{{30}} < \dfrac{{ - 65}}{{30}} < \dfrac{{ - 6}}{{30}}\) suy ra \( - 3,7 < \dfrac{{ - 13}}{6} < \dfrac{{ - 1}}{5}\) (1)
* So sánh các số: \(\dfrac{{21}}{{11}};1\dfrac{1}{2};\dfrac{3}{7}\)
Ta có: \(\dfrac{{21}}{{11}} = \dfrac{{294}}{{154}}\,;\,1\dfrac{1}{2} = \dfrac{3}{2} = \dfrac{{231}}{{154}}\,;\,\dfrac{3}{7} = \dfrac{{66}}{{154}}\)
Vì \(66 < 231 < 294\) nên \(\dfrac{{66}}{{254}} < \dfrac{{231}}{{154}} < \dfrac{{294}}{{154}}\) suy ra \(\dfrac{3}{7} < 1\dfrac{1}{2} < \dfrac{{21}}{{11}}\) (2)
Từ (1) và (2), suy ra \( - 3,7 < \dfrac{{ - 13}}{6} < \dfrac{{ - 1}}{5} < \dfrac{3}{7} < 1\dfrac{1}{2} < \dfrac{{21}}{{11}}\)
Vậy các số được sắp xếp theo thứ tự tăng dần là: \( - 3,7;\dfrac{{ - 13}}{6};\dfrac{{ - 1}}{5};\dfrac{3}{7};1\dfrac{1}{2};\dfrac{{21}}{{11}}.\)
b) Theo thứ tự giảm dần: \(\dfrac{{ - 3}}{{61}};0;\dfrac{{17}}{{48}};2\dfrac{1}{5};2,45;\dfrac{{ - 1}}{{10}}\).
* So sánh các số: \(\dfrac{{17}}{{48}};2\dfrac{1}{5};2,45\)
Ta có: \(\dfrac{{17}}{{48}} = \dfrac{{85}}{{240}};2\dfrac{1}{5} = \dfrac{{11}}{5} = \dfrac{{528}}{{240}};2,45 = \dfrac{{245}}{{100}} = \dfrac{{49}}{{20}} = \dfrac{{588}}{{240}}\)
Vì \(85 < 528 < 588\) nên \(\dfrac{{85}}{{240}} < \dfrac{{528}}{{240}} < \dfrac{{588}}{{240}}\) suy ra \(\dfrac{{17}}{{48}} < 2\dfrac{1}{5} < 2,45\) (1)
* So sánh các số: \(\dfrac{{ - 3}}{{61}};0;\dfrac{{ - 1}}{{10}}\)
Ta có: \(\dfrac{{ - 3}}{{61}} = \dfrac{{ - 30}}{{610}};0 = \dfrac{0}{{610}};\dfrac{{ - 1}}{{10}} = \dfrac{{ - 61}}{{610}}\)
Vì \( - 61 < - 30 < 0\) nên \(\dfrac{{ - 61}}{{610}} < \dfrac{{ - 30}}{{610}} < \dfrac{0}{{610}}\) nên \(\dfrac{{ - 1}}{{10}} < \dfrac{{ - 3}}{{61}} < 0\) (2)
Từ (1) và (2) suy ra \(\dfrac{{ - 1}}{{10}} < \dfrac{{ - 3}}{{61}} < 0 < \dfrac{{17}}{{48}} < 2\dfrac{1}{5} < 2,45\)
Vậy các số được sắp xếp theo thứ tự giảm dần là: \(2,45;2\dfrac{1}{5};\dfrac{{17}}{{48}};0;\dfrac{{ - 3}}{{61}};\dfrac{{ - 1}}{{10}}\).
Bài 2:
Phương pháp:
a, b: Vận dụng tính chất phân phối của phép cộng và phép nhân: \(a.\left( {b + d} \right) = a.b + a.d\)
c, d: Với hai số hữu tỉ \(x,y\), ta có: \({\left( {x.y} \right)^n} = {x^n}.{y^n};{\left( {\dfrac{x}{y}} \right)^n} = \dfrac{{{x^n}}}{{{y^n}}}\left( {y \ne 0} \right)\)
Cách giải:
a) \(\dfrac{{ - 5}}{6}.\dfrac{7}{{11}} + \dfrac{{ - 5}}{{11}}.\dfrac{4}{6} + \dfrac{5}{6}\)
\(\begin{array}{l} = \dfrac{5}{6}.\left( {\dfrac{{ - 7}}{{11}} + \dfrac{{ - 4}}{{11}} + 1} \right)\\ = \dfrac{5}{6}.\left( {\dfrac{{ - 11}}{{11}} + 1} \right)\\ = \dfrac{5}{6}.\left( { - 1 + 1} \right)\\ = \dfrac{5}{6}.0 = 0\end{array}\)
b) \(\left[ {\left( {\dfrac{{ - 3}}{8} + \dfrac{{11}}{{23}}} \right):\dfrac{5}{9} + \left( {\dfrac{{ - 5}}{8} + \dfrac{{12}}{{23}}} \right):\dfrac{5}{9}} \right].\dfrac{{ - 11}}{{325}}\)
\(\begin{array}{l} = \left[ {\left( {\dfrac{{ - 3}}{8} + \dfrac{{11}}{{23}}} \right).\dfrac{9}{5} + \left( {\dfrac{{ - 5}}{8} + \dfrac{{12}}{{23}}} \right).\dfrac{9}{5}} \right].\dfrac{{ - 11}}{{325}}\\ = \left[ {\dfrac{9}{5}.\left( {\dfrac{{ - 3}}{8} + \dfrac{{11}}{{23}} + \dfrac{{ - 5}}{8} + \dfrac{{12}}{{23}}} \right)} \right].\dfrac{{ - 11}}{{325}}\\ = \left[ {\dfrac{9}{5}.\left( {\dfrac{{ - 8}}{8} + \dfrac{{23}}{{23}}} \right)} \right].\dfrac{{ - 11}}{{325}}\\ = \dfrac{9}{5}.\left( { - 1 + 1} \right).\dfrac{{ - 11}}{{325}}\\ = \dfrac{9}{5}.0.\dfrac{{ - 11}}{{325}}\\ = 0\end{array}\)
c) \(\dfrac{{{{15}^5}}}{{{5^5}}} - {\left( { - 0,25} \right)^2}{.4^2}\)
\(\begin{array}{l} = {\left( {\dfrac{{15}}{5}} \right)^5} - {\left( { - 0,25.4} \right)^2}\\ = {3^5} - {\left( { - 1} \right)^2}\\ = 243 - 1\\ = 242\end{array}\)
d) \( - \dfrac{{{2^{15}}{{.9}^4}}}{{{6^6}{{.8}^3}}} + 0,75.\dfrac{{ - 1}}{2} + 0,375\)
\(\begin{array}{l} = - \dfrac{{{2^{15}}.{{\left( {{3^2}} \right)}^4}}}{{{{\left( {2.3} \right)}^6}.{{\left( {{2^3}} \right)}^3}}} + \left( { - 0,375} \right) + 0,375\\ = - \dfrac{{{2^{15}}{{.3}^8}}}{{{2^6}{{.3}^6}{{.2}^9}}} + \left[ {\left( { - 0,375} \right) + 0,375} \right]\\ = - \dfrac{{{2^{15}}{{.3}^8}}}{{{2^{15}}{{.3}^6}}} + 0\\ = - {3^2} = 9\end{array}\)
Bài 3:
Phương pháp:
Vận dụng quy tắc chuyển vế để tìm \(x\).
Cách giải:
a) \(\left( { - 0,4} \right).\left( {2x + \dfrac{2}{5}} \right) = - 9,4\)
\(\begin{array}{l}2x + \dfrac{2}{5} = - 9,4:\left( { - 0,4} \right)\\2x + \dfrac{2}{5} = \dfrac{{ - 94}}{{10}}:\dfrac{{\left( { - 4} \right)}}{{10}}\\2x + \dfrac{2}{5} = \dfrac{{ - 94}}{{10}}.\dfrac{{10}}{{\left( { - 4} \right)}}\\2x + \dfrac{2}{5} = \dfrac{{47}}{2}\\2x = \dfrac{{47}}{2} - \dfrac{2}{5}\end{array}\)
\(\begin{array}{l}2x = \dfrac{{235}}{{10}} - \dfrac{4}{{10}}\\2x = \dfrac{{231}}{{10}}\\x = \dfrac{{231}}{{10}}:2\\x = \dfrac{{231}}{{20}}\end{array}\)
Vậy \(x = \dfrac{{231}}{{20}}\)
b) \(\left( {\dfrac{3}{2} - x} \right):\dfrac{{ - 14}}{3} = - \dfrac{6}{7}\)
\(\begin{array}{l}\dfrac{3}{2} - x = \dfrac{{ - 6}}{7}.\dfrac{{\left( { - 14} \right)}}{3}\\\dfrac{3}{2} - x = 4\\x = \dfrac{3}{2} - 4\\x = \dfrac{3}{2} - \dfrac{8}{2}\\x = \dfrac{{ - 5}}{2}\end{array}\)
Vậy \(x = \dfrac{{ - 5}}{2}\)
c) \(x + 2.\sqrt {16} = - 3.\sqrt {49} \)
\(\begin{array}{l}x + 2.\sqrt {{4^2}} = - 2\sqrt {{7^2}} \\x + 2.4 = - 2.7\\x + 8 = - 14\\x = - 14 - 8\\x = - 22\end{array}\)
Vậy \(x = - 22\)
d) \(2 + \dfrac{1}{6} - x = 10.\sqrt {0,01} - \sqrt {\dfrac{{25}}{{36}}} \)
\(\begin{array}{l}\dfrac{{12}}{6} + \dfrac{1}{6} - x = 10.\sqrt {{{\left( {0,1} \right)}^2}} - \sqrt {\dfrac{{{5^2}}}{{{6^2}}}} \\\dfrac{{13}}{6} - x = 10.0,1 - \dfrac{5}{6}\\\dfrac{{13}}{6} - x = 1 - \dfrac{5}{6} = \dfrac{6}{6} - \dfrac{5}{6}\\\dfrac{{13}}{6} - x = \dfrac{1}{6}\\x = \dfrac{{13}}{6} - \dfrac{1}{6}\\x = \dfrac{{12}}{6}\\x = 2\end{array}\)
Vậy \(x = 2\)
Bài 4:
Phương pháp:
Diện tích xung quanh của căn phòng theo công thức tính diên tích xung quanh của hình hộp chữ nhật có ba kích thước: chiều dài là \(a\), chiều rộng là \(b\), chiều cao là \(c\) (\(a,b,c\) cùng đơn vị đo) được tính theo công thức: \({S_{xq}} = 2\left( {a + b} \right)c\)(1)
Diện tích trần của căn phòng được tính theo công thức diện tích hình chữ nhật có chiều rộng là \(a\), chiều dài là \(b\) thì \(S = ab\) (2)
Diện tích cần quét sơn = (1) + (2) – diện tích các của sổ
Số tiền phải chi trả = diện tích cần quét sơn . giá tiền \(1{m^2}\)
Cách giải:
Diện tích xung quanh của căn phòng là:
\(2.\left( {6 + 4,2} \right).3,2 = 65,28\,\left( {{m^2}} \right)\)
Diện tích trần của căn phòng là:
\(6.4,2 = 25,2\,\left( {{m^2}} \right)\)
Diện tích cần quét sơn của căn phòng là:
\(65,28 + 25,2 - 8,48 = 82\,\left( {{m^2}} \right)\)
Số tiền người đó cần phải trả để quét sơn căn phòng là:
\(82.12\,100 = 992\,200\) (đồng)
Bài 5:
Phương pháp:
Vận dụng kiến thức tia phân giác của một góc; hai góc kề nhau.
Cách giải:

a) Vì \(OG\) là tia phân giác của \(\angle COD\) nên \(\angle COG = \angle DOG = \dfrac{1}{2}\angle COD = \dfrac{1}{2}{.80^0} = {40^0}\) (tính chất tia phân giác của một góc)
Vì hai góc \(\angle COG\) và \(\angle EOG\) là hai góc kề nhau nên \(\angle COG + \angle EOG = \angle COE\)
Suy ra \({40^0} + \angle EOG = {60^0}\)
\( \Rightarrow \angle EOG = {60^0} - {40^0} = {20^0}\)
Vậy \(\angle EOG = {20^0}\)
b) Vì hai góc \(\angle COE\) và \(\angle DOE\) là hai góc kề nhau nên \(\angle COE + \angle DOE = \angle COD\)
Suy ra \({60^0} + \angle DOE = {80^0}\)
\( \Rightarrow \angle DOE = {80^0} - {60^0} = {20^0}\)
Do đó, \(\angle EOG = \angle DOE = {20^0}\)
Mặt khác \(OE\) nằm giữa hai tia \(OD\) và \(OG\) nên \(OE\) là tia phân giác của \(\angle DOG\).
Đề thi giữa kì 1 Toán 7 - Đề số 3 là một công cụ quan trọng giúp học sinh lớp 7 đánh giá năng lực và kiến thức đã học trong giai đoạn đầu năm học. Đề thi này thường bao gồm các chủ đề chính như số tự nhiên, số nguyên, phân số, tỉ lệ thức, và các bài toán đại số cơ bản. Việc làm quen với cấu trúc đề thi và các dạng bài tập thường gặp là yếu tố then chốt để đạt kết quả tốt.
Thông thường, đề thi giữa kì 1 Toán 7 - Đề số 3 sẽ được chia thành các phần sau:
Giải:
A = 23 + 32 - 51 = 8 + 9 - 5 = 12
Giải:
3x + 5 = 14
3x = 14 - 5
3x = 9
x = 9 / 3
x = 3
Giải:
Áp dụng tính chất của tỉ lệ thức, ta có:
2 * 6 = 3 * x
12 = 3x
x = 12 / 3
x = 4
Ngoài việc luyện tập đề thi, các em có thể tham khảo thêm các tài liệu ôn tập sau:
Đề thi giữa kì 1 Toán 7 - Đề số 3 là một cơ hội tốt để các em học sinh lớp 7 kiểm tra và củng cố kiến thức đã học. Hy vọng với những hướng dẫn và lời khuyên trên, các em sẽ tự tin và đạt kết quả tốt trong kỳ thi sắp tới. Chúc các em học tốt!