Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 2 Toán 7 Chân trời sáng tạo - Đề số 6, được biên soạn theo chuẩn chương trình học mới nhất. Đề thi này là tài liệu ôn tập lý tưởng giúp học sinh làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Đề thi bao gồm các dạng bài tập đa dạng, từ trắc nghiệm đến tự luận, bao phủ các kiến thức trọng tâm đã học trong học kì. Học sinh có thể tự đánh giá năng lực của mình và tìm ra những điểm cần cải thiện.
Trong các cặp tỉ số sau, cặp tỉ số nào lập thành một tỉ lệ thức?
Cho tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}.\) Khẳng định đúng là
Từ đẳng thức \(2.\left( { - 15} \right) = \left( { - 5} \right).6\), ta có thể lập được tỉ lệ thức nào?
Cho \(x,y\) là hai đại lượng tỉ lệ nghịch với nhau, biết \({x_1},{y_1}\) và \({x_2},{y_2}\) là các cặp giá trị tương ứng của chúng. Khẳng định nào sau đây là sai?
\(\frac{{{x_1}}}{{{y_2}}} = \frac{{{x_2}}}{{{y_1}}}.\)
\(\frac{{{y_1}}}{{{x_1}}} = \frac{{{x_2}}}{{{y_2}}}.\)
Nếu ba số \(a;{\rm{ }}b;{\rm{ }}c\)tương ứng tỉ lệ với \(2;5;7\)ta có dãy tỉ số bằng nhau là:
Cho đại lượng \(y\) tỉ lệ thuận với đại lượng \(x\) theo hệ số tỉ lệ \(k = - 3.\) Hệ thức liên hệ của \(y\) và \(x\) là:
Khẳng định nào sau đây không đúng?
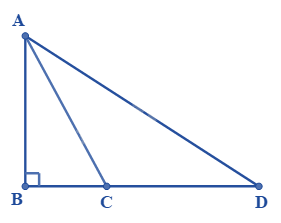
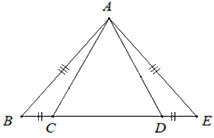
Trong hình vẽ bên, có điểm \(C\) nằm giữa \(B\) và \(D\). So sánh \(AB;AC;AD\) ta được
Trong các bộ ba đoạn thẳng sau đây. Bộ gồm ba đoạn thẳng nào là độ dài ba cạnh của một tam giác?
Cho đại lượng y tỉ lệ thuận với đại lượng x. Khi \(x = 4\) thì \(y = 16\) . Vậy hệ số tỉ lệ bằng
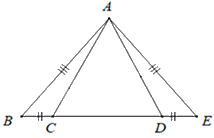
Số tam giác cân trong hình vẽ dưới đây là:
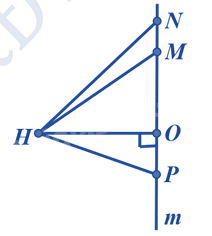
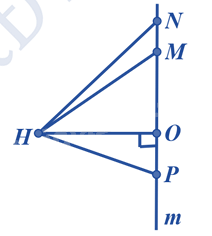
Đường vuông góc kẻ từ H xuống đường thẳng m là:
a) Tìm x biết \(\frac{6}{x} = \frac{{ - 4}}{5}\).
b) Tìm \(x;y\) biết: \(\frac{x}{5} = \frac{y}{3}\) và \(x + 2y = 33\).
c) Tìm a, b, c tỉ lệ với ba số 2; 3; -4 và a + b – c = 18.
Số học sinh lớp 7A, 7B, 7C tương ứng tỉ lệ với 21; 20; 22. Tính số học sinh của mỗi lớp, biết rằng lớp 7C có nhiều hơn lớp 7A là 2 học sinh.
Một khu đất hình chữ nhật có chiều dài và chiều rộng tỉ lệ với 8 và 5. Diện tích khu đất đó bằng \(360{m^2}\). Tính chiều dài và chiều rộng của khu đất đó.
Cho tam giác ABC cân tại A. Từ A kẻ AH vuông góc với BC tại H, trên đoạn thẳng AH lấy điểm M tùy ý (M khác A và H). Chứng minh rằng:
a) BH = CH.
b) BA > BM.
Cho tam giác ABC có trung tuyến AM. Chứng minh rằng \(AB + AC > 2AM\).
Trong các cặp tỉ số sau, cặp tỉ số nào lập thành một tỉ lệ thức?
Đáp án : A
Tỉ lệ thức là đẳng thức của hai tỉ số \(\frac{a}{b} = \frac{c}{d}\).
Ta có: \(12:18 = \frac{{12}}{{18}} = \frac{2}{3}\) nên cặp tỉ số A lập thành một tỉ lệ thức.
\(12:18 = \frac{{12}}{{18}} = \frac{2}{3} \ne \frac{3}{2}\) nên cặp tỉ số B không lập thành một tỉ lệ thức.
\(\frac{{12}}{{ - 18}} = \frac{{ - 2}}{3} \ne \frac{2}{3}\) nên cặp tỉ số C không lập thành một tỉ lệ thức.
\(\left( { - 12} \right):\left( { - 18} \right) = \frac{{ - 12}}{{ - 18}} = \frac{2}{3} \ne \frac{{ - 2}}{3}\) nên cặp tỉ số D không lập thành một tỉ lệ thức.
Cho tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}.\) Khẳng định đúng là
Đáp án : B
Dựa vào tính chất cơ bản của tỉ lệ thức.
Áp dụng tính chất cơ bản của tỉ lệ thức, ta có:
Nếu \(\frac{a}{b} = \frac{c}{d}\) thì \(ad = bc\).
Từ đẳng thức \(2.\left( { - 15} \right) = \left( { - 5} \right).6\), ta có thể lập được tỉ lệ thức nào?
Đáp án : D
Ta sử dụng tính chất: Nếu \(ad = bc\) thì \(\frac{a}{b} = \frac{c}{d};\frac{a}{c} = \frac{b}{d};\frac{d}{b} = \frac{c}{a};\frac{d}{c} = \frac{b}{a}\).
Từ đẳng thức \(2.\left( { - 15} \right) = \left( { - 5} \right).6\), ta có:
\(\frac{2}{{ - 5}} = \frac{6}{{ - 15}};\frac{2}{6} = \frac{{ - 5}}{{ - 15}};\frac{{ - 5}}{2} = \frac{{ - 15}}{6};\frac{6}{2} = \frac{{ - 15}}{{ - 5}}\).
\( \Rightarrow \) Đáp án D là đáp án đúng.
Cho \(x,y\) là hai đại lượng tỉ lệ nghịch với nhau, biết \({x_1},{y_1}\) và \({x_2},{y_2}\) là các cặp giá trị tương ứng của chúng. Khẳng định nào sau đây là sai?
\(\frac{{{x_1}}}{{{y_2}}} = \frac{{{x_2}}}{{{y_1}}}.\)
\(\frac{{{y_1}}}{{{x_1}}} = \frac{{{x_2}}}{{{y_2}}}.\)
Đáp án : B
Dựa vào tính chất của hai đại lượng tỉ lệ nghịch.
x, y là hai đại lượng tỉ lệ nghịch với nhau nên \(\frac{{{x_1}}}{{{x_2}}} = \frac{{{y_2}}}{{{y_1}}}\); \(\frac{{{x_1}}}{{{y_2}}} = \frac{{{x_2}}}{{{y_1}}}\); \({x_1}{y_1} = {x_2}{y_2}\)
\( \Rightarrow A,C,D\) đúng.
Nếu ba số \(a;{\rm{ }}b;{\rm{ }}c\)tương ứng tỉ lệ với \(2;5;7\)ta có dãy tỉ số bằng nhau là:
Đáp án : D
Dựa vào kiến thức về dãy tỉ số bằng nhau.
Vì a; b; c tương ứng tỉ lệ với 2; 5; 7 nên ta có dãy tỉ số bằng nhau là:
\(\frac{a}{2} = \frac{b}{5} = \frac{c}{7}\).
Cho đại lượng \(y\) tỉ lệ thuận với đại lượng \(x\) theo hệ số tỉ lệ \(k = - 3.\) Hệ thức liên hệ của \(y\) và \(x\) là:
Đáp án : B
Dựa vào kiến thức về hai đại lượng tỉ lệ thuận.
Đại lượng \(y\) tỉ lệ thuận với đại lượng \(x\) theo hệ số tỉ lệ \(k = - 3\) ta có hệ thức liên hệ của y và x là \(y = - 3x\).
Khẳng định nào sau đây không đúng?
Đáp án : C
Dựa vào các kiến thức về tam giác đều.
Tam giác đều là tam giác có 3 cạnh bằng nhau nên B đúng.
Tính chất: Tam giác đều có 3 góc bằng nhau, đều bằng \({60^0}\) nên A đúng.
Mọi tam giác đều luôn là tam giác cân nên D đúng.
Tam giác cân là tam giác có hai cạnh bằng nhau nên C sai.
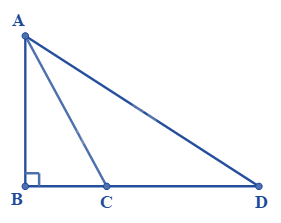
Trong hình vẽ bên, có điểm \(C\) nằm giữa \(B\) và \(D\). So sánh \(AB;AC;AD\) ta được
Đáp án : B
Dựa vào quan hệ giữa đường xiên và hình chiếu.
Vì AB < BD, C nằm giữa B và D nên BC < BD.
Do đó AB < AC < AD. (quan hệ giữa đường xiên và hình chiếu).
Trong các bộ ba đoạn thẳng sau đây. Bộ gồm ba đoạn thẳng nào là độ dài ba cạnh của một tam giác?
Đáp án : C
Dựa vào quan hệ giữa ba cạnh của một tam giác: Trong một tam giác, tổng độ dài hai cạnh bất kỳ bao giờ cũng lớn hơn độ dài cạnh còn lại.
Ta có: \(5 = 3 + 2\) nên \(5\,cm,\,3\,cm,\,2\,cm\) không là độ dài ba cạnh của một tam giác.
\(1 + 1 = 2 < 5\) nên \(5\,cm,\,1\,cm,\,1\,cm\) không là độ dài ba cạnh của một tam giác.
\(5 + 3 = 8 > 6;\,5 + 6 = 11 > 3;\,3 + 6 = 9 > 5\) nên \(5\,cm,\,3\,cm,\,6\,cm\) là độ dài ba cạnh của một tam giác.
\(5 + 5 = 10\) nên \(5\,cm,\,5\,cm,\,10\,cm\) không là độ dài ba cạnh của một tam giác.
Cho đại lượng y tỉ lệ thuận với đại lượng x. Khi \(x = 4\) thì \(y = 16\) . Vậy hệ số tỉ lệ bằng
Đáp án : A
Dựa vào kiến thức về hai đại lượng tỉ lệ thuận.
Đại lượng y tỉ lệ thuận với đại lượng x nên hệ số tỉ lệ là:
\(k = \frac{y}{x} = \frac{{16}}{4} = 4\).
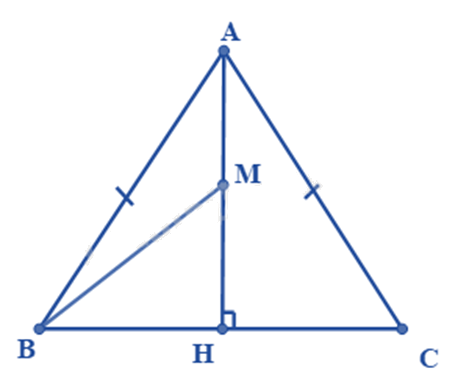
Số tam giác cân trong hình vẽ dưới đây là:
Đáp án : A
Dựa vào kiến thức về hai tam giác bằng nhau và tính chất của tam giác cân.
Ta có \(\Delta ABE\) có AB = AE nên \(\Delta ABE\) cân tại A.
Suy ra \(\widehat {ABC} = \widehat {AED}\).
\(\Delta ABC = \Delta AED\left( {c.g.c} \right)\)
Suy ra AC = AD (hai cạnh tương ứng) suy ra \(\Delta ACD\) cân tại A.
Vậy có 2 tam giác cân.
Đường vuông góc kẻ từ H xuống đường thẳng m là:
Đáp án : C
Dựa vào kiến thức về đường vuông góc.
Đường vuông góc kẻ từ H xuống đường thẳng m là HO.
a) Tìm x biết \(\frac{6}{x} = \frac{{ - 4}}{5}\).
b) Tìm \(x;y\) biết: \(\frac{x}{5} = \frac{y}{3}\) và \(x + 2y = 33\).
c) Tìm a, b, c tỉ lệ với ba số 2; 3; -4 và a + b – c = 18.
a) Dựa vào tính chất của tỉ lệ thức để tìm x.
b, c) Sử dụng tính chất của dãy tỉ số bằng nhau để tìm ẩn.
a) Ta có:
\(\begin{array}{l}\frac{6}{x} = \frac{{ - 4}}{5}\\6.5 = - 4.x\\ - 4x = 30\\x = \frac{{ - 30}}{4} = \frac{{ - 15}}{2}\end{array}\)
Vậy \(x = \frac{{ - 15}}{2}\).
b) Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{x}{5} = \frac{y}{3} = \frac{{x + 2y}}{{5 + 2.3}} = \frac{{33}}{{11}} = 3\)
Từ đó suy ra:
\(\begin{array}{l}x = 3.5 = 15\\y = 3.3 = 9\end{array}\)
Vậy x = 15; y = 9.
c) Ta có a, b, c tỉ lệ với ba số 2; 3; -4 nên ta có dãy tỉ số bằng nhau:
\(\frac{a}{2} = \frac{b}{3} = \frac{c}{{ - 4}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{2} = \frac{b}{3} = \frac{c}{{ - 4}} = \frac{{a + b - c}}{{2 + 3 - \left( { - 4} \right)}} = \frac{{18}}{9} = 2\)
Từ đó suy ra:
\(\begin{array}{l}a = 2.2 = 4\\b = 2.3 = 6\\c = 2.\left( { - 4} \right) = - 8\end{array}\)
Vậy \(a = 4;b = 6;c = - 8\).
Số học sinh lớp 7A, 7B, 7C tương ứng tỉ lệ với 21; 20; 22. Tính số học sinh của mỗi lớp, biết rằng lớp 7C có nhiều hơn lớp 7A là 2 học sinh.
Áp dụng tính chất của dãy tỉ số bằng nhau để tìm số học sinh của mỗi lớp.
Gọi số học sinh lớp 7A, 7B, 7C lần lượt là a, b, c \(\left( {a,b,c \in \mathbb{N}*,c > 2} \right)\) (học sinh)
Vì số học sinh lớp 7A, 7B, 7C tương ứng tỉ lệ với 21; 20; 22 nên ta có dãy tỉ số bằng nhau:
\(\frac{a}{{21}} = \frac{b}{{20}} = \frac{c}{{22}}\)
Do lớp 7C có nhiều hơn lớp 7A 2 học sinh nên áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{b}{{20}} = \frac{c}{{22}} = \frac{a}{{21}} = \frac{{c - a}}{{22 - 21}} = \frac{2}{1} = 2\).
Từ đó suy ra:
\(\begin{array}{l}c = 2.22 = 44\\a = 2.21 = 42\\b = 2.20 = 40\end{array}\) (Thỏa mãn)
Vậy số học sinh lớp 7A, 7B, 7C lần lượt là 42; 40; 44 học sinh.
Một khu đất hình chữ nhật có chiều dài và chiều rộng tỉ lệ với 8 và 5. Diện tích khu đất đó bằng \(360{m^2}\). Tính chiều dài và chiều rộng của khu đất đó.
Áp dụng tính chất của dãy tỉ số bằng nhau và công thức tính diện tích hình chữ nhật để tìm chiều dài và chiều rộng của khu đất đó.
Gọi chiều dài và chiều rộng của khu đất lần lượt là \(x,y\left( {x > y > 0} \right)\) \(\left( m \right)\).
Vì chiều dài và chiều rộng tỉ lệ với 8 và 5 nên ta có:
\(\frac{x}{8} = \frac{y}{5} = k\left( {k > 0} \right)\) suy ra \(x = 8k;y = 5k\).
Mà diện tích khu đất bằng \(360{m^2}\) nên ta có \(x.y = 360\) hay \(8k.5k = 360\)
\(\begin{array}{l}40{k^2} = 360\\{k^2} = 9\end{array}\)
\(k = 3\) (vì \(k > 0\))
Từ đó suy ra:
\(\begin{array}{l}x = 8.3 = 24\\y = 5.3 = 15\end{array}\)(thỏa mãn)
Vậy chiều dài và chiều rộng của khu đất đó lần lượt là \(24m\) và \(15m\).
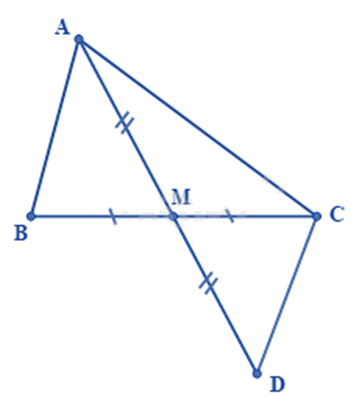
Cho tam giác ABC cân tại A. Từ A kẻ AH vuông góc với BC tại H, trên đoạn thẳng AH lấy điểm M tùy ý (M khác A và H). Chứng minh rằng:
a) BH = CH.
b) BA > BM.
a) Chứng minh \(\Delta AHB = \Delta AHC\) nên \(BH = CH\).
b) Sử dụng quan hệ giữa đường vuông góc và đường xiên để chứng minh.
a) Xét \(\Delta AHB\) và \(\Delta AHC\) có:
\(\widehat {AHB} = \widehat {AHC} = {90^0}\)
\(AB = AC\) (\(\Delta ABC\) cân tại A)
AH chung
Suy ra \(\Delta AHB = \Delta AHC\) (cạnh huyền – cạnh góc vuông)
Suy ra \(BH = CH\) (hai cạnh tương ứng) (đpcm)
b) Do M nằm giữa A và H nên HA > HM.
Ta có BH là đường vuông góc, BA và BM là các đường xiên kẻ từ B đến đường thẳng AH nên HM là hình chiếu của BM, HA là hình chiếu của AB xuống AH.
Vì HA > HM nên BA > BM.
Vậy BA > BM (đpcm).
Cho tam giác ABC có trung tuyến AM. Chứng minh rằng \(AB + AC > 2AM\).
Dựa vào kiến thức về đường trung tuyến trong tam giác.
Lấy điểm D thuộc tia đối của tia MA sao cho AM = DM.
Chứng minh \(\Delta AMB = \Delta DMC\) suy ra \(AB = CD\).
Sử dụng bất đẳng thức tam giác để chứng minh \(AB + AC > AD = 2AM\).
Do AM là trung tuyến của tam giác ABC nên ta có BM = CM.
Trên tia đối của tia MA lấy điểm D sao cho AM = DM.
Xét \(\Delta AMB\) và \(\Delta DMC\) có:
\(AM = DM\)
\(BM = CM\)
\(\widehat {AMB} = \widehat {DMC}\) (hai góc đối đỉnh)
Suy ra \(\Delta AMB = \Delta DMC\) (c.g.c) suy ra AB = CD (hai cạnh tương ứng)
Khi đó \(AB + AC = DC + AC > AD\) (bất đẳng thức tam giác)
Mà AM = DM nên AD = 2.AM
Do đó: \(AB + AC > 2AM\).
Đề thi giữa kì 2 Toán 7 Chân trời sáng tạo - Đề số 6 là một bài kiểm tra quan trọng giúp đánh giá mức độ nắm vững kiến thức của học sinh sau nửa học kì. Đề thi này không chỉ kiểm tra khả năng tính toán mà còn đánh giá khả năng vận dụng kiến thức vào giải quyết các bài toán thực tế. Bài viết này sẽ cung cấp một cái nhìn tổng quan về đề thi, phân tích các dạng bài tập thường gặp và hướng dẫn giải chi tiết một số câu hỏi điển hình.
Thông thường, đề thi giữa kì 2 Toán 7 Chân trời sáng tạo - Đề số 6 có cấu trúc bao gồm hai phần chính:
Dưới đây là một số dạng bài tập thường gặp trong đề thi giữa kì 2 Toán 7 Chân trời sáng tạo - Đề số 6:
Ví dụ 1: Giải phương trình sau: 2x + 5 = 11
Lời giải:
Vậy nghiệm của phương trình là x = 3.
Ví dụ 2: Cho tam giác ABC có AB = 3cm, AC = 4cm, BC = 5cm. Chứng minh tam giác ABC vuông tại A.
Lời giải:
Ta có: AB2 + AC2 = 32 + 42 = 9 + 16 = 25
BC2 = 52 = 25
Vì AB2 + AC2 = BC2 nên tam giác ABC vuông tại A (theo định lý Pytago đảo).
Đề thi giữa kì 2 Toán 7 Chân trời sáng tạo - Đề số 6 là một cơ hội tốt để học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán. Hy vọng với những thông tin và hướng dẫn trên, các em sẽ tự tin hơn khi bước vào kỳ thi. Chúc các em đạt kết quả tốt!