Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 2 Toán 7 Chân trời sáng tạo - Đề số 7, được biên soạn theo chuẩn chương trình học mới nhất. Đề thi này là tài liệu ôn tập lý tưởng giúp học sinh làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Đề thi bao gồm các dạng bài tập đa dạng, từ trắc nghiệm đến tự luận, bao phủ toàn bộ kiến thức trọng tâm của chương trình học kì 2. Kèm theo đề thi là đáp án chi tiết, giúp học sinh tự đánh giá kết quả và tìm ra những điểm cần cải thiện.
Nếu4.b = 5.c và b, c ≠ 0 thì:
Nếu các số x, y, z tỉ lệ với các số 6; 4; 3 thì ta có dãy tỉ số bằng nhau nào:
Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ 5. Ta có:
Cho x và y là hai đại lượng tỉ lệ thuận với nhau. Biết hệ số tỉ lệ của x đối với y là 8. Hệ số tỉ lệ của y đối với x là:
Cho biết y và x là hai đại lượng tỉ lệ nghịch theo hệ số tỉ lệ a. Ta có:
Cho tam giác ABC. Trong các khẳng định sau khẳng định nào sai?
Cho \(\Delta ABC = \Delta DEF\). Khi đó:
Cho \(\Delta ABC = \Delta DEF\), \(\hat C = {40^0}\). Khi đó:
Cho tam giác ABC có: \(\widehat A = {45^0};\widehat B = {60^0}\). So sánh các cạnh của tam giác ABC là:
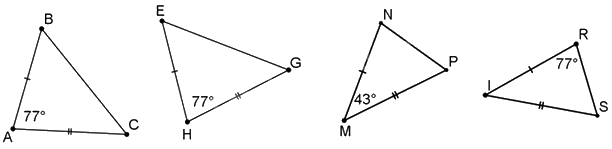
Cho hình vẽ, hãy chỉ ra hai tam giác bằng nhau.
Cho tam giác ABC cân tại A, cạnh AB = 5cm. Tính độ dài cạnh AC?
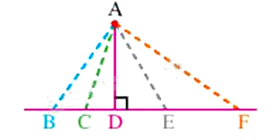
Cho hình vẽ, có bao nhiêu đường xiên kẻ từ điểm A đến đường thẳng BF?
1. Tìm x biết: \(\frac{x}{4} = \frac{7}{5}\).
2. Cho biết đại lượng x và y tỉ lệ thuận với nhau và khi x = 20 thì y = 12.
a) Tìm hệ số tỉ lệ của y đối với x và biểu diễn y theo x.
b) Tính giá trị của x khi \(y = \frac{{ - 1}}{3}\).
Ba lớp 7A, 7B, 7C thu tập tặng bạn vùng bão. Biết số vở của ba lớp lần lượt tỉ lệ với 3; 4; 5 và tổng số vở của lớp 7A và 7C là 240 cuốn. Tính số vở của mỗi lớp thu được.
Một đội công nhân có 15 người làm xong công việc trong 90 ngày. Hỏi cần bổ sung thêm bao nhiêu công nhân để hoàn thành công việc đó chỉ trong 50 ngày.
So sánh các cạnh của tam giác ABC có \(\widehat A = {50^0},\,\widehat B = {60^0}\).
Cho tam giác ABC có AB = AC, N là trung điểm của BC.
a) Chứng minh \(\Delta ABN = \Delta ACN\).
b) Qua A kẻ đường thẳng a vuông góc với AN. Chứng minh a // BC.
c) Vẽ điểm F sao cho N là trung điểm của AF. Chứng minh AB + AC > 2AN.
Nếu4.b = 5.c và b, c ≠ 0 thì:
Đáp án : B
Dựa vào tính chất của tỉ lệ thức: Nếu \(ad = bc\left( {a,b,c,d \ne 0} \right)\) thì ta có các tỉ lệ thức:
\(\frac{a}{b} = \frac{c}{d};\frac{a}{c} = \frac{b}{d};\frac{d}{b} = \frac{c}{a};\frac{d}{c} = \frac{b}{a}\)
Nếu \(4.b = 5.c\) thì ta có các tỉ lệ thức:
\(\frac{4}{c} = \frac{5}{b};\frac{4}{5} = \frac{c}{b};\frac{c}{4} = \frac{b}{5};\frac{5}{4} = \frac{b}{c}\) nên B đúng.
Nếu các số x, y, z tỉ lệ với các số 6; 4; 3 thì ta có dãy tỉ số bằng nhau nào:
Đáp án : D
Dựa vào tính chất dãy tỉ số bằng nhau.
Nếu các số x, y, z tỉ lệ với các số 6; 4; 3 thì ta có dãy tỉ số bằng nhau:
\(\frac{x}{6} = \frac{y}{4} = \frac{z}{3}\).
Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ 5. Ta có:
Đáp án : A
Dựa vào kiến thức về hai đại lượng tỉ lệ thuận.
Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ 5 ta có công thức \(y = 5x\).
Cho x và y là hai đại lượng tỉ lệ thuận với nhau. Biết hệ số tỉ lệ của x đối với y là 8. Hệ số tỉ lệ của y đối với x là:
Đáp án : B
Khi đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ k (khác 0) thì x cũng tỉ lệ thuận với y theo hệ số tỉ lệ \(\frac{1}{k}\) và ta nói hai đại lượng đó tỉ lệ thuận với nhau.
Hệ số tỉ lệ của x đối với y là 8 nên hệ số tỉ lệ của y đối với x là \(\frac{1}{8}\).
Cho biết y và x là hai đại lượng tỉ lệ nghịch theo hệ số tỉ lệ a. Ta có:
Đáp án : B
Dựa vào kiến thức về hai đại lượng tỉ lệ nghịch.
Nếu y và x là hai đại lượng tỉ lệ nghịch theo hệ số tỉ lệ a thì \(y = \frac{a}{x}\) hay \(xy = a\).
Cho tam giác ABC. Trong các khẳng định sau khẳng định nào sai?
Đáp án : C
Dựa vào quan hệ giữa ba cạnh của một tam giác.
Trong một tam giác, tổng độ dài hai cạnh bất kỳ bao giờ cũng lớn hơn độ dài cạnh còn lại nên A, B và D đúng.
Trong một tam giác, hiệu độ dài hai cạnh bất kỳ bao giờ cũng nhỏ hơn độ dài cạnh còn lại nên C sai.
Cho \(\Delta ABC = \Delta DEF\). Khi đó:
Đáp án : A
Dựa vào các kiến thức về hai tam giác bằng nhau.
\(\Delta ABC = \Delta DEF\) nên ta có:
\(\begin{array}{l}AB = DE\\BC = EF\\AC = DF\end{array}\)
Cho \(\Delta ABC = \Delta DEF\), \(\hat C = {40^0}\). Khi đó:
Đáp án : A
Dựa vào các kiến thức về hai tam giác bằng nhau.
\(\Delta ABC = \Delta DEF\) nên ta có:
\(\widehat C = \widehat F = {40^0}\).
Cho tam giác ABC có: \(\widehat A = {45^0};\widehat B = {60^0}\). So sánh các cạnh của tam giác ABC là:
Đáp án : A
Áp dụng định lí tổng ba góc của một tam giác và quan hệ giữa góc và cạnh đối diện trong một tam giác.
Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^0}\\\widehat C = {180^0} - \widehat A - \widehat B\\ = {180^0} - {45^0} - {60^0}\\ = {75^0}\end{array}\)
Trong tam giác ABC, ta có:
\(\widehat C > \widehat B > \widehat A\left( {{{75}^0} > {{60}^0} > {{45}^0}} \right)\) suy ra \(AB > AC > BC\).
Cho hình vẽ, hãy chỉ ra hai tam giác bằng nhau.
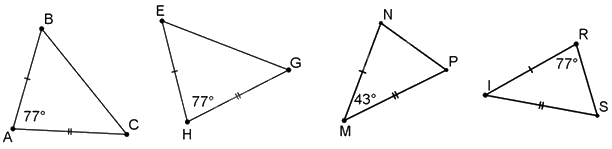
Đáp án : A
Dựa vào các trường hợp bằng nhau của hai tam giác để xác định.
Trong các tam giác trên, chỉ có \(\Delta ABC = \Delta HEG\)(c.g.c) đủ điều kiện để xác định bằng nhau.
Cho tam giác ABC cân tại A, cạnh AB = 5cm. Tính độ dài cạnh AC?
Đáp án : D
Dựa vào tính chất của tam giác cân.
Tam giác ABC cân tại A nên AB = AC = 5cm.
Cho hình vẽ, có bao nhiêu đường xiên kẻ từ điểm A đến đường thẳng BF?
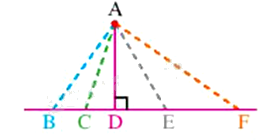
Đáp án : D
Dựa vào kiến thức về đường xiên.
Trong hình trên, có 4 đường xiên là: AB, AC, AE, AF.
1. Tìm x biết: \(\frac{x}{4} = \frac{7}{5}\).
2. Cho biết đại lượng x và y tỉ lệ thuận với nhau và khi x = 20 thì y = 12.
a) Tìm hệ số tỉ lệ của y đối với x và biểu diễn y theo x.
b) Tính giá trị của x khi \(y = \frac{{ - 1}}{3}\).
1. Dựa vào tính chất của tỉ lệ thức để tìm x.
2. Sử dụng kiến thức về hai đại lượng tỉ lệ thuận với nhau.
1. Ta có:
\(\begin{array}{l}\frac{x}{4} = \frac{7}{5}\\5x = 7.4\\5x = 28\\x = \frac{{28}}{5}\end{array}\)
Vậy \(x = \frac{{28}}{5}\).
2.
a) Vì đại lượng x và y tỉ lệ thuận với nhau nên \(y = kx\) (\(k \ne 0\))
Vì khi x = 20 thì y = 12 nên \(20 = k.12\) suy ra \(k = \frac{{20}}{{12}} = \frac{5}{3}\).
Vậy hệ số tỉ lệ của y đối với x là \(k = \frac{5}{3}\) và \(y = \frac{5}{3}x\).
b) Thay \(y = \frac{{ - 1}}{3}\) vào công thức ta được: \(\frac{{ - 1}}{3} = \frac{5}{3}x\) suy ra \(x = \frac{{ - 1}}{5}\).
Ba lớp 7A, 7B, 7C thu tập tặng bạn vùng bão. Biết số vở của ba lớp lần lượt tỉ lệ với 3; 4; 5 và tổng số vở của lớp 7A và 7C là 240 cuốn. Tính số vở của mỗi lớp thu được.
Áp dụng tính chất của dãy tỉ số bằng nhau để tìm số vở của mỗi lớp thu được.
Gọi số vở lớp 7A, 7B, 7C lần lượt là a, b, c \(\left( {a,b,c \in \mathbb{N}*} \right)\) (cuốn)
Vì số học sinh lớp 7A, 7B, 7C tương ứng tỉ lệ với 3; 4; 5 nên ta có dãy tỉ số bằng nhau:
\(\frac{a}{3} = \frac{b}{4} = \frac{c}{5}\)
Do tổng số vở của lớp 7A và 7C là 240 nên áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{b}{4} = \frac{a}{3} = \frac{c}{5} = \frac{{a + c}}{{3 + 5}} = \frac{{240}}{8} = 30\).
Từ đó suy ra:
\(\begin{array}{l}a = 30.3 = 90\\b = 30.4 = 120\\c = 30.5 = 150\end{array}\) (Thỏa mãn)
Vậy số vở lớp 7A, 7B, 7C thu được lần lượt là 90; 120; 150 cuốn.
Một đội công nhân có 15 người làm xong công việc trong 90 ngày. Hỏi cần bổ sung thêm bao nhiêu công nhân để hoàn thành công việc đó chỉ trong 50 ngày.
Áp dụng tính chất của hai đại lượng tỉ lệ nghịch với nhau.
Gọi số công nhân mà đội cần để hoàn thành công việc trong 50 ngày là x (người) (\(x \in N*,x > 15\))
Vì lượng công việc là không thay đổi nên số công nhân và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch.
Theo tính chất của hai đại lượng tỉ lệ nghịch, ta có:
\(15.90 = x.50\) suy ra \(x = \frac{{15.90}}{{50}} = 27\).
Vậy đội cần bổ sung thêm 27 – 15 = 12 công nhân để hoàn thành công việc trong 50 ngày.
So sánh các cạnh của tam giác ABC có \(\widehat A = {50^0},\,\widehat B = {60^0}\).
Áp dụng định lí tổng ba góc của một tam giác và quan hệ giữa góc và cạnh đối diện trong một tam giác.
Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^0}\\\widehat C = {180^0} - \widehat A - \widehat B\\ = {180^0} - {50^0} - {60^0}\\ = {70^0}\end{array}\)
Trong tam giác ABC, ta có:
\(\widehat C > \widehat B > \widehat A\left( {{{70}^0} > {{60}^0} > {{50}^0}} \right)\) suy ra \(AB > AC > BC\).
Cho tam giác ABC có AB = AC, N là trung điểm của BC.
a) Chứng minh \(\Delta ABN = \Delta ACN\).
b) Qua A kẻ đường thẳng a vuông góc với AN. Chứng minh a // BC.
c) Vẽ điểm F sao cho N là trung điểm của AF. Chứng minh AB + AC > 2AN.
a) Dựa vào các trường hợp bằng nhau của hai tam giác.
b) Chứng minh \(AN \bot BC\) suy ra a // BC.
c) Dựa vào bất đẳng thức tam giác để chứng minh.
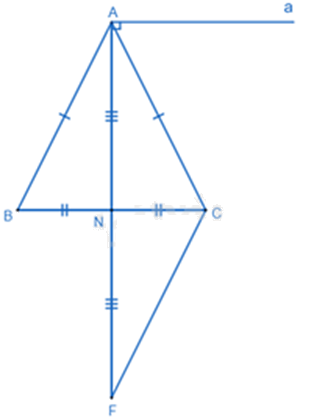
a) Xét \(\Delta ABN\) và \(\Delta ACN\) có:
\(\begin{array}{l}AB = AC(gt)\\BN = CN(gt)\\AN\,chung\end{array}\)
Suy ra \(\Delta ABN = \Delta ACN\)(c.c.c) (đpcm)
b) Ta có \(\Delta ABN = \Delta ACN\) suy ra \(\widehat {ANB} = \widehat {ANC}\).
Mà hai góc này là hai góc kề bù nên \(\widehat {ANB} = \widehat {ANC} = \frac{{{{180}^0}}}{2} = {90^0}\).
Do đó \(AN \bot BC\). Mà \(a \bot AN\) (gt)
Suy ra \(a//BC\) (từ vuông góc đến song song) (đpcm).
c) Xét \(\Delta ABN\) và \(\Delta FCN\) có:
\(\begin{array}{l}AN = NF(gt)\\BN = CN(gt)\end{array}\)
\(\widehat {ANB} = \widehat {FNC}\) (hai góc đối đỉnh)
Suy ra \(\Delta ABN = \Delta FCN\)(c.g.c) (đpcm)
Suy ra AB = CF.
Xét \(\Delta ACF\) có:
\(\begin{array}{l}CF + AC > AF\\AB + AC > 2AN\end{array}\)
(vì AB = CF và AF = 2AN) (đpcm).
Đề thi giữa kì 2 Toán 7 Chân trời sáng tạo - Đề số 7 là một công cụ đánh giá quan trọng giúp học sinh kiểm tra mức độ nắm vững kiến thức và kỹ năng đã học trong học kì 2. Đề thi này không chỉ giúp học sinh tự đánh giá năng lực mà còn là cơ hội để các em làm quen với cấu trúc đề thi thực tế, từ đó chuẩn bị tốt hơn cho các kỳ thi quan trọng.
Đề thi thường bao gồm các phần sau:
Các dạng bài tập thường xuất hiện trong đề thi:
Ví dụ: Tính giá trị của biểu thức A = (1/2 + 1/3) * 6/5. Hướng dẫn: Thực hiện các phép tính trong ngoặc trước, sau đó thực hiện phép nhân.
Ví dụ: Giải phương trình 2x + 3 = 7. Hướng dẫn: Chuyển số hạng tự do sang vế phải, sau đó chia cả hai vế cho hệ số của x.
Ví dụ: Cho hai đường thẳng a và b cắt đường thẳng c. Biết góc so le trong bằng nhau. Chứng minh a song song b. Hướng dẫn: Sử dụng dấu hiệu nhận biết hai đường thẳng song song.
Để đạt kết quả tốt trong kỳ thi giữa kì 2 Toán 7 Chân trời sáng tạo - Đề số 7, học sinh cần luyện tập thường xuyên các dạng bài tập khác nhau. Việc luyện tập không chỉ giúp học sinh nắm vững kiến thức mà còn rèn luyện kỹ năng giải toán nhanh và chính xác.
Giaitoan.edu.vn cung cấp đầy đủ các tài liệu ôn thi Toán 7, bao gồm đề thi, bài tập, đáp án và hướng dẫn giải chi tiết. Chúng tôi cam kết mang đến cho học sinh những tài liệu chất lượng, giúp các em học tập hiệu quả và đạt kết quả cao trong các kỳ thi.
| Chương | Kiến thức trọng tâm |
|---|---|
| Số hữu tỉ | Phân số, số thập phân, phần trăm, so sánh và sắp xếp số hữu tỉ |
| Biểu thức đại số | Biến, biểu thức, giá trị của biểu thức |
| Phương trình bậc nhất một ẩn | Giải phương trình, ứng dụng phương trình |
Hy vọng với những thông tin và hướng dẫn trên, các em học sinh sẽ tự tin hơn khi làm bài thi giữa kì 2 Toán 7 Chân trời sáng tạo - Đề số 7. Chúc các em học tập tốt!