Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 1 Toán 7 - Đề số 9, một công cụ hữu ích giúp các em học sinh ôn luyện và đánh giá năng lực bản thân trước kỳ thi quan trọng. Đề thi được biên soạn theo chương trình học Toán 7, bao gồm các dạng bài tập thường gặp và có đáp án chi tiết.
Với đề thi này, các em có thể tự tin làm bài và đạt kết quả tốt nhất trong kỳ thi giữa kì 1 Toán 7.
Phần trắc nghiệm (3 điểm) Câu 1: Số đối của số hữu tỉ ( - 0,25) là
Phần trắc nghiệm (3 điểm)
Câu 1: Số đối của số hữu tỉ \( - 0,25\) là
A. \( - 0,25.\)
B. \(\frac{{ - 1}}{4}.\)
C. \( - 4.\)
D. \(0,25.\)
Câu 2: Trong các số sau, số nào là số hữu tỉ âm?
A. \(\frac{0}{{ - 2}}\)
B. \(\frac{{ - 2}}{{ - 1}}\)
C. \( - \frac{1}{2}\)
D. \(\frac{{ - \left( { - 2} \right)}}{3}\)
Câu 3: Khi biểu diễu số hữu tỉ a và b trên trục số nằm ngang ta thấy điểm a nằm bên phải điểm b thì
A. \(a < b.\)
B. \(a > b.\)
C. \(a = b.\)
D. \(a = - b.\)
Câu 4: Kết quả của phép tính \({7^{10}}:7\) viết dưới dạng lũy thừa là
A. \({7^9}.\)
B. \({7^{11}}.\)
C. \({7^{10}}.\)
D. \({1^{10}}.\)
Câu 5: Với \(a,b,c\)là ba số hữu tỉ bất kì, nếu \(a - b = c\) thì
A. \(a = b + c.\)
B. \(a = - b + c.\)
C. \(a = b - c.\)
D. \(a = - b - c.\)
Câu 6: Với \(x,y,z\)là ba số hữu tỉ bất kì, sau khi bỏ ngoặc ta được \(x - \left( {y + z} \right)\) bằng
A. \(x - y + z.\)
B. \(x - y - z.\)
C. \(x + y - z.\)
D. \(x + y + z.\)
Câu 7: Những đồ vật sau có dạng hình gì?

A. Hình hộp chữ nhật
B. Hình vuông
C. Hình lập phương
D. Hình chữ nhật
Câu 8: Cho hình lập phương \(ABCD.MNPQ\) có độ dài cạnh là \(2{\rm{\;cm}}\). Tính tổng diện tích các mặt của hình lập phương.
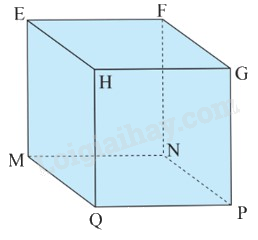
A. \(8{\rm{\;c}}{{\rm{m}}^2}\).
B. \(12{\rm{\;c}}{{\rm{m}}^2}\).
C. \(24{\rm{\;c}}{{\rm{m}}^2}\).
D. \(20{\rm{\;c}}{{\rm{m}}^2}\).
Câu 9: Chọn phát biểu đúng trong các phát biểu sau:
A. Hình lăng trụ tam giác có 4 mặt, 6 đỉnh;
B. Hình lăng trụ tam giác có 5 mặt, 6 đỉnh;
C. Hình lăng trụ tam giác có 6 mặt, 5 đỉnh;
D. Hình lăng trụ tam giác có 4 mặt, 4 đỉnh.
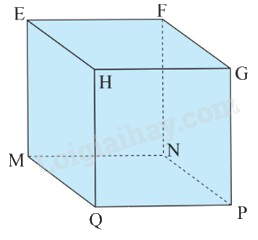
Câu 10: Quan sát hình lập phương EFGH.MNPQ, biết \({\rm{MN}} = 3{\rm{\;cm}}\), độ dài các cạnh \({\rm{EF}},{\rm{NF}}\) bằng bao nhiêu?
A. \({\rm{EF}} = {\rm{NF}} = 3{\rm{\;cm}}\)
B. \({\rm{EF}} = 3{\rm{\;cm}},{\rm{NF}} = 6{\rm{\;cm}}\)
C. \({\rm{EF}} = {\rm{NF}} = 6{\rm{\;cm}}\)
D. Các đáp án đều sai
Câu 11: Cho hình lăng trụ đứng tam giác có kích thước như hình vẽ.
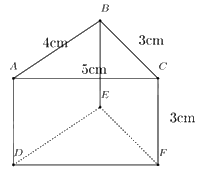
Diện tích xung quanh của hình lăng trụ đứng trên là:
A. 36cm2.
B. 30cm2.
C. 36cm3.
D. 30cm3.
Câu 12: Cho các khẳng định sau:
(I). Hai góc đối đỉnh thì bằng nhau.
(II). Hai góc bằng nhau thì đối đỉnh.
(III). Hai góc kề bù là hai góc vừa kề nhau, vừa bù nhau.
Số khẳng định đúng là:
A. 1.
B. 2.
C. 3.
D. 0.
Phần tự luận (7 điểm)
Bài 1: (0,5 điểm) So sánh hai số hữu tỉ sau: \(0,25\) và \(\frac{1}{3}\)
Bài 2: (2,0 điểm) Thực hiện phép tính:
a) \(\left( { - 0,25} \right).40\; + 3\)
b) \(\frac{1}{7} \cdot \frac{{ - 3}}{8} + \frac{{ - 13}}{8} \cdot \frac{1}{7}\)
c) \(\left[ {\left( {\frac{2}{3} - \frac{1}{4}} \right) + {{\left( { - 2} \right)}^2}.3} \right] - 1\)
Bài 3: (2,0 điểm) Tìm x, biết:
a) \(x - 4 = \frac{1}{2}\)
b) \(2.\left( {x - 1} \right) = {3^3} - 1\)
Bài 4: (1,5 điểm) Một nhà kho có dạng hình lăng trụ đứng, đáy là hình thang vuông. Chiều cao của hình lăng trụ đứng (là chiều dài của nhà kho) bằng \(6{\rm{\;m}}\). Đường cao của đáy (là chiều rộng của nhà kho) bằng \(5{\rm{\;m}}\). Các cạnh đáy của hình thang vuông dài \(3{\rm{\;m}}\) và \(4{\rm{\;m}}\). Tính thể tích của nhà kho.
Bài 5: (1,0 điểm)Một phòng học hình hộp chữ nhật có chiều dài \(8{\rm{\;m}}\), chiều rộng \(5{\rm{\;m}}\), chiều cao \(4{\rm{\;m}}\). Người ta quét vôi bên trong lớp học, kể cả trần. Biết tổng diện tích các cửa ra vào và cửa sổ là \(10{\rm{\;}}{{\rm{m}}^2}\). Tính diện tích phải quét vôi.
-------- Hết --------
Phần trắc nghiệm (3 điểm)
Câu 1: D | Câu 2: C | Câu 3: B | Câu 4: A | Câu 5: A | Câu 6: B |
Câu 7. A | Câu 8. C | Câu 9. B | Câu 10. A | Câu 11. A | Câu 12. B |
Câu 1: Số đối của số hữu tỉ \( - 0,25\) là
A. \( - 0,25.\) | B. \(\frac{{ - 1}}{4}.\) |
C. \( - 4.\) | D. \(0,25.\) |
Phương pháp
Số đối của một số hữu tỉ a là – a.
Lời giải
Số đối của -0,25 là –(-0,25) = 0,25.
Đáp án D.
Câu 2: Trong các số sau, số nào là số hữu tỉ âm?
A. \(\frac{0}{{ - 2}}\) | B. \(\frac{{ - 2}}{{ - 1}}\) |
C. \( - \frac{1}{2}\) | D. \(\frac{{ - \left( { - 2} \right)}}{3}\) |
Phương pháp
Số hữu tỉ âm là số nhỏ hơn 0.
Lời giải
\(\frac{0}{{ - 2}} = 0\) nên không phải số hữu tỉ âm.
\(\frac{{ - 2}}{{ - 1}} = 2 > 0\) nên không phải số hữu tỉ âm.
\( - \frac{1}{2} < 0\) nên là số hữu tỉ âm.
\(\frac{{ - \left( { - 2} \right)}}{3} = \frac{2}{3} > 0\) nên không phải là số hữu tỉ âm.
Đáp án C.
Câu 3:Khi biểu diễu số hữu tỉ a và b trên trục số nằm ngang ta thấy điểm a nằm bên phải điểm b thì
A. \(a < b.\) | B. \(a > b.\) |
C. \(a = b.\) | D. \(a = - b.\) |
Phương pháp
Theo thứ tự trong tập hợp số hữu tỉ thì số nằm bên phải sẽ là số lớn hơn.
Lời giải
Vì điểm a nằm bên phải điểm b nên a > b.
Đáp án B.
Câu 4: Kết quả của phép tính \({7^{10}}:7\) viết dưới dạng lũy thừa là
A. \({7^9}.\) | B. \({7^{11}}.\) |
C. \({7^{10}}.\) | D. \({1^{10}}.\) |
Phương pháp
Sử dụng quy tắc chia hai lũy thừa cùng cơ số.
Lời giải
\({7^{10}}:7 = {7^{10 - 1}} = {7^9}\).
Đáp án A.
Câu 5: Với \(a,b,c\)là ba số hữu tỉ bất kì, nếu \(a - b = c\) thì
A. \(a = b + c.\) | B. \(a = - b + c.\) |
C. \(a = b - c.\) | D. \(a = - b - c.\) |
Phương pháp
Dựa vào quy tắc chuyển vế.
Lời giải
Nếu a – b = c thì a = b + c.
Đáp án A.
Câu 6: Với \(x,y,z\)là ba số hữu tỉ bất kì, sau khi bỏ ngoặc ta được \(x - \left( {y + z} \right)\) bằng
A. \(x - y + z.\) | B. \(x - y - z.\) |
C. \(x + y - z.\) | D. \(x + y + z.\) |
Phương pháp
Dựa vào quy tắc dấu ngoặc.
Lời giải
Ta có: x – (y + z) = x – y – z.
Đáp án B.
Câu 7: Những đồ vật sau có dạng hình gì?

A. Hình hộp chữ nhật | B. Hình vuông |
C. Hình lập phương | D. Hình chữ nhật |
Phương pháp
Quan sát hình vẽ.
Lời giải
Những đồ vật trên là hình hộp chữ nhật.
Đáp án A.
Câu 8: Cho hình lập phương \(ABCD.MNPQ\) có độ dài cạnh là \(2{\rm{\;cm}}\). Tính tổng diện tích các mặt của hình lập phương.
A. \(8{\rm{\;c}}{{\rm{m}}^2}\). | B. \(12{\rm{\;c}}{{\rm{m}}^2}\). |
C. \(24{\rm{\;c}}{{\rm{m}}^2}\). | D. \(20{\rm{\;c}}{{\rm{m}}^2}\). |
Phương pháp
Tổng diện tích các mặt của hình lập phương bằng 6 lần diện tích một mặt của hình lập phương.
Lời giải
Diện tích một mặt của hình lập phương là: 2.2 = 4 cm2.
Tổng diện tích các mặt của hình lập phương là: 6.4 = 24 cm2.
Đáp án C.
Câu 9: Chọn phát biểu đúng trong các phát biểu sau:A. Hình lăng trụ tam giác có 4 mặt, 6 đỉnh;B. Hình lăng trụ tam giác có 5 mặt, 6 đỉnh;
C. Hình lăng trụ tam giác có 6 mặt, 5 đỉnh;
D. Hình lăng trụ tam giác có 4 mặt, 4 đỉnh.
Phương pháp
Dựa kiến thức về hình lăng trụ tam giác.
Lời giải
Hình lăng trụ tam giác có 2 mặt đáy và 3 mặt bên nên có 2 + 3 = 5 mặt.
Hình lăng trụ tam giác có 6 đỉnh.
Đáp án B.
Câu 10: Quan sát hình lập phương EFGH.MNPQ, biết \({\rm{MN}} = 3{\rm{\;cm}}\), độ dài các cạnh \({\rm{EF}},{\rm{NF}}\) bằng bao nhiêu?
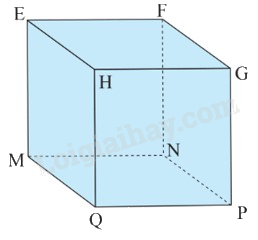
A. \({\rm{EF}} = {\rm{NF}} = 3{\rm{\;cm}}\) | B. \({\rm{EF}} = 3{\rm{\;cm}},{\rm{NF}} = 6{\rm{\;cm}}\) |
C. \({\rm{EF}} = {\rm{NF}} = 6{\rm{\;cm}}\) | D. Các đáp án đều sai |
Phương pháp
Xác định các cặp cạnh bằng nhau để tính độ dài EF, NF.
Lời giải
Vì EFGH.MNPQ là hình lập phương nên tất cả các cạnh bằng nhau suy ra EF = NF = MN = 3cm.
Đáp án A.
Câu 11: Cho hình lăng trụ đứng tam giác có kích thước như hình vẽ.
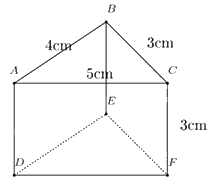
Diện tích xung quanh của hình lăng trụ đứng trên là:
A. 36cm2. | B. 30cm2. |
C. 36cm3. | D. 30cm3. |
Phương pháp
Dựa vào công thức tính diện tích xung quanh của hình lăng trụ.
Lời giải
Diện tích xung quanh của hình lăng trụ trên là:
\({S_{xq}} = \left( {4 + 3 + 5} \right).3 = 36\left( {c{m^2}} \right)\)
Đáp án A.
Câu 12: Cho các khẳng định sau:(I). Hai góc đối đỉnh thì bằng nhau.(II). Hai góc bằng nhau thì đối đỉnh.(III). Hai góc kề bù là hai góc vừa kề nhau, vừa bù nhau.
Số khẳng định đúng là:
A. 1. | B. 2. |
C. 3. | D. 0. |
Phương pháp
Dựa vào kiến thức về góc đã học.
Lời giải
Hai góc đối đỉnh thì bằng nhau nên (I) đúng.
Hai góc bằng nhau chưa chắc đã đối đỉnh nên (II) sai.
Hai góc kề bù là hai góc kề nhau và bù nhau nên (III) đúng.
Đáp án B.
Phần tự luận.
Bài 1: (0,5 điểm) So sánh hai số hữu tỉ sau: \(0,25\) và \(\frac{1}{3}\).
Phương pháp
Viết hai phân số về dạng số hữu tỉ để so sánh.
Lời giải
Ta có: \(0,25 = \frac{1}{4}\).
Vì 4 > 3 nên \(\frac{1}{4} < \frac{1}{3}\).
Vậy \(0,25 < \frac{1}{3}\).
Bài 2: (2,0 điểm) Thực hiện phép tính:
a) \(\left( { - 0,25} \right).40\; + 3\) | b) \(\frac{1}{7} \cdot \frac{{ - 3}}{8} + \frac{{ - 13}}{8} \cdot \frac{1}{7}\) |
c) \(\left[ {\left( {\frac{2}{3} - \frac{1}{4}} \right) + {{\left( { - 2} \right)}^2}.3} \right] - 1\) |
Phương pháp
Dựa vào quy tắc tính với số hữu tỉ để tính.
Lời giải
a) \(\left( { - 0,25} \right).40\; + 3\) = -10 + 3 = -7 | b) \(\frac{1}{7} \cdot \frac{{ - 3}}{8} + \frac{{ - 13}}{8} \cdot \frac{1}{7}\) \(\begin{array}{l} = \frac{1}{7}\left( {\frac{{ - 3}}{8} + \frac{{ - 13}}{8}} \right)\\ = \frac{1}{7}\left( {\frac{{ - 3 - 13}}{8}} \right)\\ = \frac{1}{7}.\frac{{ - 16}}{8}\\ = \frac{1}{7}.\left( { - 2} \right)\\ = \frac{{ - 2}}{7}\end{array}\) |
c) \(\left[ {\left( {\frac{2}{3} - \frac{1}{4}} \right) + {{\left( { - 2} \right)}^2}.3} \right] - 1\) \( = {\rm{ }}\;\left[ {\frac{5}{{12}} + 12} \right] - 1\) \( = {\rm{ }}\;\frac{{149}}{{12}} - 1\) \( = {\rm{ }}\frac{{137}}{{12}}\) |
Bài 3: (2,0 điểm) Tìm x, biết:
a) \(x - 4 = \frac{1}{2}\) | b) \(2.\left( {x - 1} \right) = {3^3} - 1\) |
Phương pháp
Sử dụng quy tắc chuyển vế để tìm x.
Lời giải
\({\rm{a) }}x - 4 = \frac{1}{2}\) \({\rm{ }}x = \frac{1}{2} + 4\) \({\rm{ }}x = \frac{9}{2}\) Vậy \({\rm{ }}x = \frac{9}{2}\). | b) \(2.\left( {x - 1} \right) = {3^3} - 1\) \(2.\left( {x - 1} \right) = 8\) \(x - 1 = 4\) \(\begin{array}{l}x = 4 + 1\\x = 5\end{array}\) Vậy \(x = 5\). |
Bài 4: (1,5 điểm) Một nhà kho có dạng hình lăng trụ đứng, đáy là hình thang vuông. Chiều cao của hình lăng trụ đứng (là chiều dài của nhà kho) bằng \(6{\rm{\;m}}\). Đường cao của đáy (là chiều rộng của nhà kho) bằng \(5{\rm{\;m}}\). Các cạnh đáy của hình thang vuông dài \(3{\rm{\;m}}\) và \(4{\rm{\;m}}\). Tính thể tích của nhà kho.
Phương pháp
Tính diện tích đáy hình lăng trụ đứng.
Tính thể tích nhà kho.
Lời giải
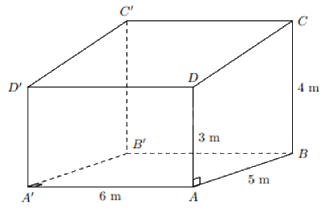
Gọi nhà kho có dạng hình lăng trụ đứng ABCD.A’B’C’D’.Diện tích đáy hình lăng trụ là:
\({S_{ABCD}} = \frac{1}{2}\left( {3 + 4} \right).5 = 17,5\left( {c{m^2}} \right)\)
Thể tích nhà kho là:
\({V_{kho}} = {S_{ABCD}}.AA' = 17,5.6 = 105\left( {c{m^3}} \right)\)
Vậy thể tích nhà kho là 105cm3.
Bài 5: (1,0 điểm)Một phòng học hình hộp chữ nhật có chiều dài \(8{\rm{\;m}}\), chiều rộng \(5{\rm{\;m}}\), chiều cao \(4{\rm{\;m}}\). Người ta quét vôi bên trong lớp học, kể cả trần. Biết tổng diện tích các cửa ra vào và cửa sổ là \(10{\rm{\;}}{{\rm{m}}^2}\). Tính diện tích phải quét vôi.
Phương pháp
Tính chu vi sàn căn phòng.
Tính diện tích xung quanh của căn phòng.
Tính diện tích trần.
Tính diện tích phải quét vôi = diện tích xung quanh – diện tích trần – diện tích các cửa.
Lời giải
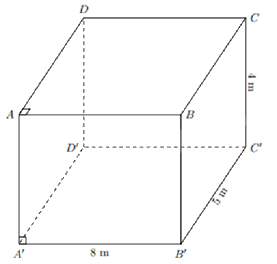
Gọi căn phòng là hình hộp chữ nhật ABCD.A’B’C’D’.
Chu vi sàn căn phòng hình chữ nhật là: 2 . (8 + 5) = 26 (m)Diện tích xung quanh của căn phòng là: Sxq = 26.4 = 104(m2)Diện tích trần của căn phòng là: Strần = 8.5 = 40(m2)Diện tích phải quét vôi là: S = Sxq – Strần - 10 = 104 + 40 - 10 = 134(m2)Vậy diện tích phải quyét vôi là 134m2.
Tải về
Phần trắc nghiệm (3 điểm)
Câu 1: Số đối của số hữu tỉ \( - 0,25\) là
A. \( - 0,25.\)
B. \(\frac{{ - 1}}{4}.\)
C. \( - 4.\)
D. \(0,25.\)
Câu 2: Trong các số sau, số nào là số hữu tỉ âm?
A. \(\frac{0}{{ - 2}}\)
B. \(\frac{{ - 2}}{{ - 1}}\)
C. \( - \frac{1}{2}\)
D. \(\frac{{ - \left( { - 2} \right)}}{3}\)
Câu 3: Khi biểu diễu số hữu tỉ a và b trên trục số nằm ngang ta thấy điểm a nằm bên phải điểm b thì
A. \(a < b.\)
B. \(a > b.\)
C. \(a = b.\)
D. \(a = - b.\)
Câu 4: Kết quả của phép tính \({7^{10}}:7\) viết dưới dạng lũy thừa là
A. \({7^9}.\)
B. \({7^{11}}.\)
C. \({7^{10}}.\)
D. \({1^{10}}.\)
Câu 5: Với \(a,b,c\)là ba số hữu tỉ bất kì, nếu \(a - b = c\) thì
A. \(a = b + c.\)
B. \(a = - b + c.\)
C. \(a = b - c.\)
D. \(a = - b - c.\)
Câu 6: Với \(x,y,z\)là ba số hữu tỉ bất kì, sau khi bỏ ngoặc ta được \(x - \left( {y + z} \right)\) bằng
A. \(x - y + z.\)
B. \(x - y - z.\)
C. \(x + y - z.\)
D. \(x + y + z.\)
Câu 7: Những đồ vật sau có dạng hình gì?

A. Hình hộp chữ nhật
B. Hình vuông
C. Hình lập phương
D. Hình chữ nhật
Câu 8: Cho hình lập phương \(ABCD.MNPQ\) có độ dài cạnh là \(2{\rm{\;cm}}\). Tính tổng diện tích các mặt của hình lập phương.
A. \(8{\rm{\;c}}{{\rm{m}}^2}\).
B. \(12{\rm{\;c}}{{\rm{m}}^2}\).
C. \(24{\rm{\;c}}{{\rm{m}}^2}\).
D. \(20{\rm{\;c}}{{\rm{m}}^2}\).
Câu 9: Chọn phát biểu đúng trong các phát biểu sau:
A. Hình lăng trụ tam giác có 4 mặt, 6 đỉnh;
B. Hình lăng trụ tam giác có 5 mặt, 6 đỉnh;
C. Hình lăng trụ tam giác có 6 mặt, 5 đỉnh;
D. Hình lăng trụ tam giác có 4 mặt, 4 đỉnh.
Câu 10: Quan sát hình lập phương EFGH.MNPQ, biết \({\rm{MN}} = 3{\rm{\;cm}}\), độ dài các cạnh \({\rm{EF}},{\rm{NF}}\) bằng bao nhiêu?
A. \({\rm{EF}} = {\rm{NF}} = 3{\rm{\;cm}}\)
B. \({\rm{EF}} = 3{\rm{\;cm}},{\rm{NF}} = 6{\rm{\;cm}}\)
C. \({\rm{EF}} = {\rm{NF}} = 6{\rm{\;cm}}\)
D. Các đáp án đều sai
Câu 11: Cho hình lăng trụ đứng tam giác có kích thước như hình vẽ.
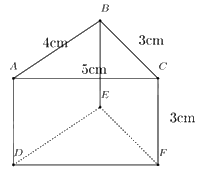
Diện tích xung quanh của hình lăng trụ đứng trên là:
A. 36cm2.
B. 30cm2.
C. 36cm3.
D. 30cm3.
Câu 12: Cho các khẳng định sau:
(I). Hai góc đối đỉnh thì bằng nhau.
(II). Hai góc bằng nhau thì đối đỉnh.
(III). Hai góc kề bù là hai góc vừa kề nhau, vừa bù nhau.
Số khẳng định đúng là:
A. 1.
B. 2.
C. 3.
D. 0.
Phần tự luận (7 điểm)
Bài 1: (0,5 điểm) So sánh hai số hữu tỉ sau: \(0,25\) và \(\frac{1}{3}\)
Bài 2: (2,0 điểm) Thực hiện phép tính:
a) \(\left( { - 0,25} \right).40\; + 3\)
b) \(\frac{1}{7} \cdot \frac{{ - 3}}{8} + \frac{{ - 13}}{8} \cdot \frac{1}{7}\)
c) \(\left[ {\left( {\frac{2}{3} - \frac{1}{4}} \right) + {{\left( { - 2} \right)}^2}.3} \right] - 1\)
Bài 3: (2,0 điểm) Tìm x, biết:
a) \(x - 4 = \frac{1}{2}\)
b) \(2.\left( {x - 1} \right) = {3^3} - 1\)
Bài 4: (1,5 điểm) Một nhà kho có dạng hình lăng trụ đứng, đáy là hình thang vuông. Chiều cao của hình lăng trụ đứng (là chiều dài của nhà kho) bằng \(6{\rm{\;m}}\). Đường cao của đáy (là chiều rộng của nhà kho) bằng \(5{\rm{\;m}}\). Các cạnh đáy của hình thang vuông dài \(3{\rm{\;m}}\) và \(4{\rm{\;m}}\). Tính thể tích của nhà kho.
Bài 5: (1,0 điểm)Một phòng học hình hộp chữ nhật có chiều dài \(8{\rm{\;m}}\), chiều rộng \(5{\rm{\;m}}\), chiều cao \(4{\rm{\;m}}\). Người ta quét vôi bên trong lớp học, kể cả trần. Biết tổng diện tích các cửa ra vào và cửa sổ là \(10{\rm{\;}}{{\rm{m}}^2}\). Tính diện tích phải quét vôi.
-------- Hết --------
Phần trắc nghiệm (3 điểm)
Câu 1: D | Câu 2: C | Câu 3: B | Câu 4: A | Câu 5: A | Câu 6: B |
Câu 7. A | Câu 8. C | Câu 9. B | Câu 10. A | Câu 11. A | Câu 12. B |
Câu 1: Số đối của số hữu tỉ \( - 0,25\) là
A. \( - 0,25.\) | B. \(\frac{{ - 1}}{4}.\) |
C. \( - 4.\) | D. \(0,25.\) |
Phương pháp
Số đối của một số hữu tỉ a là – a.
Lời giải
Số đối của -0,25 là –(-0,25) = 0,25.
Đáp án D.
Câu 2: Trong các số sau, số nào là số hữu tỉ âm?
A. \(\frac{0}{{ - 2}}\) | B. \(\frac{{ - 2}}{{ - 1}}\) |
C. \( - \frac{1}{2}\) | D. \(\frac{{ - \left( { - 2} \right)}}{3}\) |
Phương pháp
Số hữu tỉ âm là số nhỏ hơn 0.
Lời giải
\(\frac{0}{{ - 2}} = 0\) nên không phải số hữu tỉ âm.
\(\frac{{ - 2}}{{ - 1}} = 2 > 0\) nên không phải số hữu tỉ âm.
\( - \frac{1}{2} < 0\) nên là số hữu tỉ âm.
\(\frac{{ - \left( { - 2} \right)}}{3} = \frac{2}{3} > 0\) nên không phải là số hữu tỉ âm.
Đáp án C.
Câu 3:Khi biểu diễu số hữu tỉ a và b trên trục số nằm ngang ta thấy điểm a nằm bên phải điểm b thì
A. \(a < b.\) | B. \(a > b.\) |
C. \(a = b.\) | D. \(a = - b.\) |
Phương pháp
Theo thứ tự trong tập hợp số hữu tỉ thì số nằm bên phải sẽ là số lớn hơn.
Lời giải
Vì điểm a nằm bên phải điểm b nên a > b.
Đáp án B.
Câu 4: Kết quả của phép tính \({7^{10}}:7\) viết dưới dạng lũy thừa là
A. \({7^9}.\) | B. \({7^{11}}.\) |
C. \({7^{10}}.\) | D. \({1^{10}}.\) |
Phương pháp
Sử dụng quy tắc chia hai lũy thừa cùng cơ số.
Lời giải
\({7^{10}}:7 = {7^{10 - 1}} = {7^9}\).
Đáp án A.
Câu 5: Với \(a,b,c\)là ba số hữu tỉ bất kì, nếu \(a - b = c\) thì
A. \(a = b + c.\) | B. \(a = - b + c.\) |
C. \(a = b - c.\) | D. \(a = - b - c.\) |
Phương pháp
Dựa vào quy tắc chuyển vế.
Lời giải
Nếu a – b = c thì a = b + c.
Đáp án A.
Câu 6: Với \(x,y,z\)là ba số hữu tỉ bất kì, sau khi bỏ ngoặc ta được \(x - \left( {y + z} \right)\) bằng
A. \(x - y + z.\) | B. \(x - y - z.\) |
C. \(x + y - z.\) | D. \(x + y + z.\) |
Phương pháp
Dựa vào quy tắc dấu ngoặc.
Lời giải
Ta có: x – (y + z) = x – y – z.
Đáp án B.
Câu 7: Những đồ vật sau có dạng hình gì?

A. Hình hộp chữ nhật | B. Hình vuông |
C. Hình lập phương | D. Hình chữ nhật |
Phương pháp
Quan sát hình vẽ.
Lời giải
Những đồ vật trên là hình hộp chữ nhật.
Đáp án A.
Câu 8: Cho hình lập phương \(ABCD.MNPQ\) có độ dài cạnh là \(2{\rm{\;cm}}\). Tính tổng diện tích các mặt của hình lập phương.
A. \(8{\rm{\;c}}{{\rm{m}}^2}\). | B. \(12{\rm{\;c}}{{\rm{m}}^2}\). |
C. \(24{\rm{\;c}}{{\rm{m}}^2}\). | D. \(20{\rm{\;c}}{{\rm{m}}^2}\). |
Phương pháp
Tổng diện tích các mặt của hình lập phương bằng 6 lần diện tích một mặt của hình lập phương.
Lời giải
Diện tích một mặt của hình lập phương là: 2.2 = 4 cm2.
Tổng diện tích các mặt của hình lập phương là: 6.4 = 24 cm2.
Đáp án C.
Câu 9: Chọn phát biểu đúng trong các phát biểu sau:A. Hình lăng trụ tam giác có 4 mặt, 6 đỉnh;B. Hình lăng trụ tam giác có 5 mặt, 6 đỉnh;
C. Hình lăng trụ tam giác có 6 mặt, 5 đỉnh;
D. Hình lăng trụ tam giác có 4 mặt, 4 đỉnh.
Phương pháp
Dựa kiến thức về hình lăng trụ tam giác.
Lời giải
Hình lăng trụ tam giác có 2 mặt đáy và 3 mặt bên nên có 2 + 3 = 5 mặt.
Hình lăng trụ tam giác có 6 đỉnh.
Đáp án B.
Câu 10: Quan sát hình lập phương EFGH.MNPQ, biết \({\rm{MN}} = 3{\rm{\;cm}}\), độ dài các cạnh \({\rm{EF}},{\rm{NF}}\) bằng bao nhiêu?
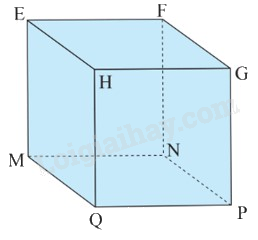
A. \({\rm{EF}} = {\rm{NF}} = 3{\rm{\;cm}}\) | B. \({\rm{EF}} = 3{\rm{\;cm}},{\rm{NF}} = 6{\rm{\;cm}}\) |
C. \({\rm{EF}} = {\rm{NF}} = 6{\rm{\;cm}}\) | D. Các đáp án đều sai |
Phương pháp
Xác định các cặp cạnh bằng nhau để tính độ dài EF, NF.
Lời giải
Vì EFGH.MNPQ là hình lập phương nên tất cả các cạnh bằng nhau suy ra EF = NF = MN = 3cm.
Đáp án A.
Câu 11: Cho hình lăng trụ đứng tam giác có kích thước như hình vẽ.
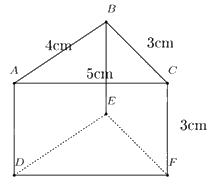
Diện tích xung quanh của hình lăng trụ đứng trên là:
A. 36cm2. | B. 30cm2. |
C. 36cm3. | D. 30cm3. |
Phương pháp
Dựa vào công thức tính diện tích xung quanh của hình lăng trụ.
Lời giải
Diện tích xung quanh của hình lăng trụ trên là:
\({S_{xq}} = \left( {4 + 3 + 5} \right).3 = 36\left( {c{m^2}} \right)\)
Đáp án A.
Câu 12: Cho các khẳng định sau:(I). Hai góc đối đỉnh thì bằng nhau.(II). Hai góc bằng nhau thì đối đỉnh.(III). Hai góc kề bù là hai góc vừa kề nhau, vừa bù nhau.
Số khẳng định đúng là:
A. 1. | B. 2. |
C. 3. | D. 0. |
Phương pháp
Dựa vào kiến thức về góc đã học.
Lời giải
Hai góc đối đỉnh thì bằng nhau nên (I) đúng.
Hai góc bằng nhau chưa chắc đã đối đỉnh nên (II) sai.
Hai góc kề bù là hai góc kề nhau và bù nhau nên (III) đúng.
Đáp án B.
Phần tự luận.
Bài 1: (0,5 điểm) So sánh hai số hữu tỉ sau: \(0,25\) và \(\frac{1}{3}\).
Phương pháp
Viết hai phân số về dạng số hữu tỉ để so sánh.
Lời giải
Ta có: \(0,25 = \frac{1}{4}\).
Vì 4 > 3 nên \(\frac{1}{4} < \frac{1}{3}\).
Vậy \(0,25 < \frac{1}{3}\).
Bài 2: (2,0 điểm) Thực hiện phép tính:
a) \(\left( { - 0,25} \right).40\; + 3\) | b) \(\frac{1}{7} \cdot \frac{{ - 3}}{8} + \frac{{ - 13}}{8} \cdot \frac{1}{7}\) |
c) \(\left[ {\left( {\frac{2}{3} - \frac{1}{4}} \right) + {{\left( { - 2} \right)}^2}.3} \right] - 1\) |
Phương pháp
Dựa vào quy tắc tính với số hữu tỉ để tính.
Lời giải
a) \(\left( { - 0,25} \right).40\; + 3\) = -10 + 3 = -7 | b) \(\frac{1}{7} \cdot \frac{{ - 3}}{8} + \frac{{ - 13}}{8} \cdot \frac{1}{7}\) \(\begin{array}{l} = \frac{1}{7}\left( {\frac{{ - 3}}{8} + \frac{{ - 13}}{8}} \right)\\ = \frac{1}{7}\left( {\frac{{ - 3 - 13}}{8}} \right)\\ = \frac{1}{7}.\frac{{ - 16}}{8}\\ = \frac{1}{7}.\left( { - 2} \right)\\ = \frac{{ - 2}}{7}\end{array}\) |
c) \(\left[ {\left( {\frac{2}{3} - \frac{1}{4}} \right) + {{\left( { - 2} \right)}^2}.3} \right] - 1\) \( = {\rm{ }}\;\left[ {\frac{5}{{12}} + 12} \right] - 1\) \( = {\rm{ }}\;\frac{{149}}{{12}} - 1\) \( = {\rm{ }}\frac{{137}}{{12}}\) |
Bài 3: (2,0 điểm) Tìm x, biết:
a) \(x - 4 = \frac{1}{2}\) | b) \(2.\left( {x - 1} \right) = {3^3} - 1\) |
Phương pháp
Sử dụng quy tắc chuyển vế để tìm x.
Lời giải
\({\rm{a) }}x - 4 = \frac{1}{2}\) \({\rm{ }}x = \frac{1}{2} + 4\) \({\rm{ }}x = \frac{9}{2}\) Vậy \({\rm{ }}x = \frac{9}{2}\). | b) \(2.\left( {x - 1} \right) = {3^3} - 1\) \(2.\left( {x - 1} \right) = 8\) \(x - 1 = 4\) \(\begin{array}{l}x = 4 + 1\\x = 5\end{array}\) Vậy \(x = 5\). |
Bài 4: (1,5 điểm) Một nhà kho có dạng hình lăng trụ đứng, đáy là hình thang vuông. Chiều cao của hình lăng trụ đứng (là chiều dài của nhà kho) bằng \(6{\rm{\;m}}\). Đường cao của đáy (là chiều rộng của nhà kho) bằng \(5{\rm{\;m}}\). Các cạnh đáy của hình thang vuông dài \(3{\rm{\;m}}\) và \(4{\rm{\;m}}\). Tính thể tích của nhà kho.
Phương pháp
Tính diện tích đáy hình lăng trụ đứng.
Tính thể tích nhà kho.
Lời giải
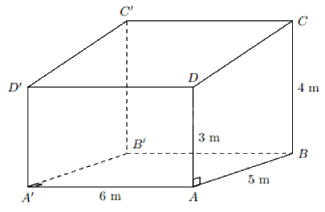
Gọi nhà kho có dạng hình lăng trụ đứng ABCD.A’B’C’D’.Diện tích đáy hình lăng trụ là:
\({S_{ABCD}} = \frac{1}{2}\left( {3 + 4} \right).5 = 17,5\left( {c{m^2}} \right)\)
Thể tích nhà kho là:
\({V_{kho}} = {S_{ABCD}}.AA' = 17,5.6 = 105\left( {c{m^3}} \right)\)
Vậy thể tích nhà kho là 105cm3.
Bài 5: (1,0 điểm)Một phòng học hình hộp chữ nhật có chiều dài \(8{\rm{\;m}}\), chiều rộng \(5{\rm{\;m}}\), chiều cao \(4{\rm{\;m}}\). Người ta quét vôi bên trong lớp học, kể cả trần. Biết tổng diện tích các cửa ra vào và cửa sổ là \(10{\rm{\;}}{{\rm{m}}^2}\). Tính diện tích phải quét vôi.
Phương pháp
Tính chu vi sàn căn phòng.
Tính diện tích xung quanh của căn phòng.
Tính diện tích trần.
Tính diện tích phải quét vôi = diện tích xung quanh – diện tích trần – diện tích các cửa.
Lời giải
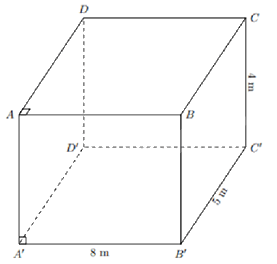
Gọi căn phòng là hình hộp chữ nhật ABCD.A’B’C’D’.
Chu vi sàn căn phòng hình chữ nhật là: 2 . (8 + 5) = 26 (m)Diện tích xung quanh của căn phòng là: Sxq = 26.4 = 104(m2)Diện tích trần của căn phòng là: Strần = 8.5 = 40(m2)Diện tích phải quét vôi là: S = Sxq – Strần - 10 = 104 + 40 - 10 = 134(m2)Vậy diện tích phải quyét vôi là 134m2.
Đề thi giữa kì 1 Toán 7 - Đề số 9 là một bài kiểm tra quan trọng, đánh giá mức độ nắm vững kiến thức và kỹ năng giải toán của học sinh sau một nửa học kỳ. Đề thi thường bao gồm các chủ đề chính như số hữu tỉ, số thực, biểu thức đại số, phương trình bậc nhất một ẩn, bất đẳng thức và các ứng dụng thực tế của toán học.
Cấu trúc đề thi có thể khác nhau tùy theo từng trường và giáo viên, nhưng thường bao gồm các phần sau:
Ví dụ 1: Giải phương trình 2x + 3 = 7
Lời giải:
Ví dụ 2: Tìm giá trị của x để biểu thức 3x - 5 > 1
Lời giải:
Để chuẩn bị tốt nhất cho đề thi giữa kì 1 Toán 7 - Đề số 9, học sinh nên ôn tập kỹ các kiến thức và kỹ năng đã học trong sách giáo khoa, sách bài tập và các tài liệu tham khảo khác. Ngoài ra, học sinh cũng nên làm thêm các đề thi thử để làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Giaitoan.edu.vn là một website học toán online uy tín, cung cấp đầy đủ các tài liệu học tập, bài giảng, đề thi và đáp án chi tiết cho học sinh các cấp. Với đội ngũ giáo viên giàu kinh nghiệm và phương pháp giảng dạy hiện đại, Giaitoan.edu.vn sẽ giúp học sinh học toán hiệu quả và đạt kết quả tốt nhất.
| Chủ đề | Nội dung chính |
|---|---|
| Số hữu tỉ | Phép cộng, trừ, nhân, chia; so sánh; giá trị tuyệt đối |
| Số thực | Biểu diễn trên trục số; so sánh; phép toán |
| Biểu thức đại số | Thu gọn; tính giá trị |
| Phương trình bậc nhất một ẩn | Giải phương trình; ứng dụng |
| Bất đẳng thức | Giải bất đẳng thức; ứng dụng |
Hy vọng với những thông tin chi tiết và hữu ích trên, các em học sinh sẽ tự tin hơn khi làm Đề thi giữa kì 1 Toán 7 - Đề số 9 và đạt kết quả cao nhất.