Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 2 Toán 7 Chân trời sáng tạo - Đề số 10, được biên soạn theo chương trình học mới nhất. Đề thi này là tài liệu ôn tập lý tưởng giúp học sinh làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Đề thi bao gồm các dạng bài tập khác nhau, từ trắc nghiệm đến tự luận, bao phủ toàn bộ kiến thức trọng tâm của chương trình học kì 2. Học sinh có thể tự đánh giá năng lực của mình và tìm ra những điểm cần cải thiện.
Từ tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\) (giả thiết các tỉ số đều có nghĩa) ta suy ra đẳng thức:
Từ đẳng thức 2.12 = 8.3 ta có thể lập được bao nhiêu tỉ lệ thức?
Cho biết đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ 2. Hãy biểu diễn y theo x?
Cho biết đại lượng x và y tỉ lệ nghịch với nhau và khi x = 2 thì y = 12. Hệ số tỉ lệ là:
Tổng số đo các góc của tam giác bằng
Cho \(\Delta MNP = \Delta LKQ\), MN = 3cm, MP = 4cm, NP = 5cm, \(\widehat M = {90^0}\). Khi đó:
Tam giác ABC có AB = 8cm, BC = 6cm, AC = 4cm. So sánh các góc của tam giác ta có:
Bộ ba độ dài nào sau đây là 3 cạnh của một tam giác?
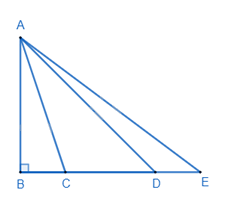
Cho hình vẽ. So sánh độ dài các đoạn thẳng AB, AC, AD, AE.
Cho tam giác MNK có MN = NK. Khi đó:
Cho tam giác ABC cân tại C. Khi đó
Đường vuông góc kẻ từ điểm A đến đường thẳng m là
Tìm x, y biết:
a) \(\frac{x}{6} = \frac{4}{3}\)
b) \(7:x = - 9:4\)
c) \(\frac{x}{7} = \frac{y}{3}\) và \(x - y = - 16\)
Tổng kết cuối học kì 1, số học sinh giỏi của ba lớp 7A, 7B, 7C lần lượt tỉ lệ với 4; 3; 2. Biết tổng số học sinh giỏi của cả ba lớp là 45 em. Hỏi mỗi lớp 7A, 7B, 7C có bao nhiêu học sinh giỏi?
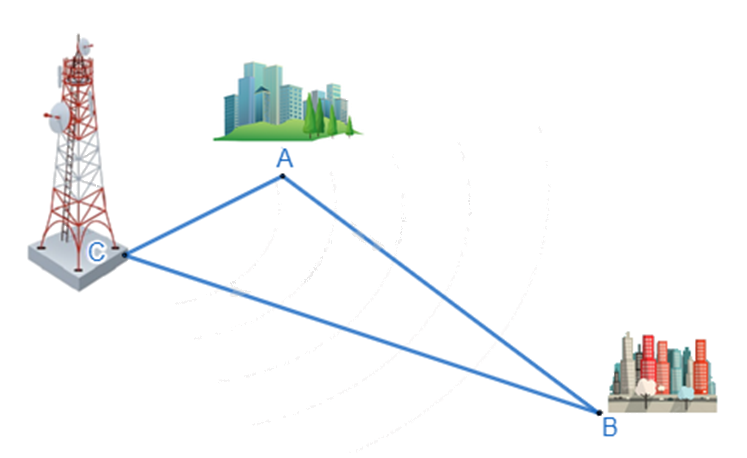
Ba thành phố ở ba địa điểm A, B, C không thẳng hàng như hình vẽ, biết AC = 30 km, AB = 90 km. Nếu đặt ở địa điểm C máy phát sóng truyền thanh có bán kính hoạt động 60km thì thành phố B có nhận được tín hiệu không? Vì sao?
Cho ∆DFE cân tại E. Gọi M là trung điểm của DF.a) Chứng minh: \(\Delta EDM{\rm{ }} = {\rm{ }}\Delta EFM\).b) Chứng minh \(EM \bot DF\).c) Từ M vẽ MA \( \bot \) ED tại A, MB \( \bot \) EF tại B. Chứng minh AB // DF.
Cho ba số a, b, c khác 0 thỏa mãn: \(\frac{{ab}}{{a + b}} = \frac{{bc}}{{b + c}} = \frac{{ca}}{{c + a}}\).
Tính giá trị của biểu thức \(M = \frac{{2ab + 3bc + ca}}{{2{a^2} + 3{b^2} + {c^2}}}\).
Từ tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\) (giả thiết các tỉ số đều có nghĩa) ta suy ra đẳng thức:
Đáp án : C
Dựa vào kiến thức về tỉ lệ thức.
Từ tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\) ta suy ra \(a.d = b.c\)
Từ đẳng thức 2.12 = 8.3 ta có thể lập được bao nhiêu tỉ lệ thức?
Đáp án : D
Dựa vào kiến thức về tỉ lệ thức.
Từ đẳng thức 2.12 = 8.3 ta có thể lập được 4 tỉ lệ thức là:
\(\frac{2}{3} = \frac{8}{{12}};\frac{2}{8} = \frac{3}{{12}};\frac{3}{2} = \frac{{12}}{8};\frac{8}{2} = \frac{{12}}{3}\).
Cho biết đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ 2. Hãy biểu diễn y theo x?
Đáp án : B
Dựa vào kiến thức về hai đại lượng tỉ lệ thuận.
Vì đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ 2 nên ta có công thức \(y = 2x\).
Cho biết đại lượng x và y tỉ lệ nghịch với nhau và khi x = 2 thì y = 12. Hệ số tỉ lệ là:
Đáp án : A
Dựa vào kiến thức về hai đại lượng tỉ lệ nghịch.
Vì y tỉ lệ nghịch với x theo hệ số tỉ lệ a nên \(a = xy = 2.12 = 24\).
Tổng số đo các góc của tam giác bằng
Đáp án : C
Dựa vào kiến thức về tổng ba góc của một tam giác.
Tổng số đo các góc của tam giác là \({180^0}\).
Cho \(\Delta MNP = \Delta LKQ\), MN = 3cm, MP = 4cm, NP = 5cm, \(\widehat M = {90^0}\). Khi đó:
Đáp án : A
Dựa vào đặc điểm của hai tam giác bằng nhau.
Ta có \(\Delta MNP = \Delta LKQ\) suy ra \(MN = KL = 3cm;\widehat M = \widehat L = {90^0}\) suy ra đáp án A đúng.
Tam giác ABC có AB = 8cm, BC = 6cm, AC = 4cm. So sánh các góc của tam giác ta có:
Đáp án : C
Dựa vào quan hệ giữa góc và cạnh đối diện trong tam giác để so sánh.
Trong tam giác ABC có AC < BC < AB (4cm < 6cm < 8cm) suy ra \(\widehat B < \widehat A < \widehat C\).
Bộ ba độ dài nào sau đây là 3 cạnh của một tam giác?
Đáp án : C
Dựa vào quan hệ giữa ba cạnh của một tam giác.
Ta có 3 + 4 = 7 < 8 nên 3cm, 4cm, 8cm không thể là ba cạnh của một tam giác.
Ta có 3 + 7 = 10 nên 10cm, 7cm, 3cm không thể là ba cạnh của một tam giác.
Ta có 4 + 5 = 9 nên 9cm, 5cm, 4cm không thể là ba cạnh của một tam giác.
Vậy chỉ có 6cm, 7cm, 10cm là ba cạnh của một tam giác.
Cho hình vẽ. So sánh độ dài các đoạn thẳng AB, AC, AD, AE.
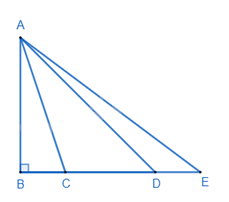
Đáp án : A
Dựa vào mối quan hệ giữa đường vuông góc và đường xiên.
Vì AB là đường vuông góc kẻ từ A xuống BE nên AB nhỏ nhất.
Quan sát hình vẽ ta thấy C nằm giữa B và D nên BC < BD suy ra AC < AD.
Mà D lại nằm giữa B và E nên BD < BE suy ra AD < AE.
Suy ra AB < AC < AD < AE.
Cho tam giác MNK có MN = NK. Khi đó:
Đáp án : D
Dựa vào kiến thức về tam giác cân.
Tam giác MNK có MN = NK là tam giác cân tại N.
Cho tam giác ABC cân tại C. Khi đó
Đáp án : A
Dựa vào kiến thức về tam giác cân.
Tam giác ABC cân tại C nên \(\widehat A = \widehat B\).
Đường vuông góc kẻ từ điểm A đến đường thẳng m là
Đáp án : C
Dựa vào kiến thức về đường vuông góc.
Đường vuông góc kẻ từ điểm A đến đường thẳng m làđường thẳng kẻ từ A đến m và vuông góc với m.
Tìm x, y biết:
a) \(\frac{x}{6} = \frac{4}{3}\)
b) \(7:x = - 9:4\)
c) \(\frac{x}{7} = \frac{y}{3}\) và \(x - y = - 16\)
Áp dụng tính chất của tỉ lệ thức.
a) Ta có: \(\frac{x}{6} = \frac{4}{3}\)
Suy ra \(x.3 = 4.6\)
\(x = \frac{{4.6}}{3} = 8\)
Vậy x = 8.
b) Ta có: \(7:x = - 9:4\)
Suy ra \(\frac{7}{x} = \frac{{ - 9}}{4}\)
\(\begin{array}{l}7.4 = - 9.x\\x = \frac{{7.4}}{{ - 9}} = \frac{{ - 28}}{9}\end{array}\)
Vậy \(x = \frac{{ - 28}}{9}\).
c) Ta có: \(\frac{x}{7} = \frac{y}{3}\) và \(x - y = - 16\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{x}{7} = \frac{y}{3} = \frac{x - y}{7 - 3} = \frac{-16}{4} = -4\)
Suy ra \(\frac{x}{7} = -4\) nên \(x = -4.7 = -28\)
\(\frac{y}{3} = -4\) nên \(y = -4.3 = -12\)
Vậy \(x = -28; y = -12\)
Tổng kết cuối học kì 1, số học sinh giỏi của ba lớp 7A, 7B, 7C lần lượt tỉ lệ với 4; 3; 2. Biết tổng số học sinh giỏi của cả ba lớp là 45 em. Hỏi mỗi lớp 7A, 7B, 7C có bao nhiêu học sinh giỏi?
Áp dụng tính chất của dãy tỉ số bằng nhau.
Gọi số học sinh giỏi của ba lớp 7A, 7B, 7C lần lượt là a, b, c. \(\left( {a,b,c \in \mathbb{N}*} \right)\)
Vì số học sinh giỏi của ba lớp 7A, 7B, 7C lần lượt tỉ lệ với 4; 3; 2 nên ta có: \(\frac{a}{4} = \frac{b}{3} = \frac{c}{2}\).
Vì tổng số học sinh giỏi của cả ba lớp là 45 em ta có a + b + c = 45.
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{4} = \frac{b}{3} = \frac{c}{2} = \frac{{a + b + c}}{{4 + 3 + 2}} = \frac{{45}}{9} = 5\)
Suy ra \(a = 5.4 = 20\)
\(\begin{array}{l}b = 5.3 = 15\\c = 5.2 = 10\end{array}\)
Vậy số học sinh giỏi của lớp 7A, 7B, 7C lần lượt là 20; 15; 10 học sinh.
Ba thành phố ở ba địa điểm A, B, C không thẳng hàng như hình vẽ, biết AC = 30 km, AB = 90 km. Nếu đặt ở địa điểm C máy phát sóng truyền thanh có bán kính hoạt động 60km thì thành phố B có nhận được tín hiệu không? Vì sao?
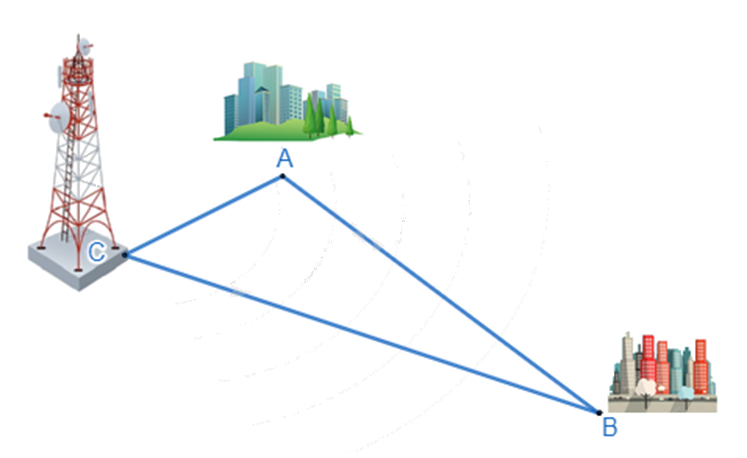
Sử dụng hệ quả của bất đẳng thức tam giác.
Theo đề bài AC = 30km, AB = 90km suy ra AC < AB.
Trong ∆ABC có: CB > AB – AC (hệ quả của bất đẳng thức tam giác)
Suy ra CB > 90 – 30 = 60km
Vậy nếu đặt tại C máy phát sóng truyền thanh có bán kính hoạt động bằng 60km thì thành phố B không nhận được tín hiệu.
Cho ∆DFE cân tại E. Gọi M là trung điểm của DF.a) Chứng minh: \(\Delta EDM{\rm{ }} = {\rm{ }}\Delta EFM\).b) Chứng minh \(EM \bot DF\).c) Từ M vẽ MA \( \bot \) ED tại A, MB \( \bot \) EF tại B. Chứng minh AB // DF.
a) Chứng minh \(\Delta EDM{\rm{ }} = {\rm{ }}\Delta EFM\) theo trường hợp cạnh – cạnh – cạnh.
b) Chứng minh \(\widehat {EMD} = \widehat {EMF} = {90^0}\) suy ra \(EM \bot DF\).
c) Chứng minh \(\Delta EAB\) cân nên \(\widehat {EAB} = \widehat {EDF}\), mà hai góc ở vị trí đồng vị nên AB // DF.
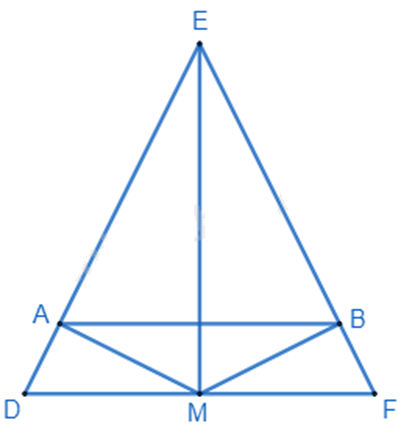
a) Xét \(\Delta EDM\) và \(\Delta EFM\) có:
DE = EF (tam giác DFE cân tại E)
DM = MF (M là trung điểm của DF)
ME chung
Suy ra \(\Delta EDM = \Delta EFM\) (c.c.c) (đpcm)
b) \(\Delta EDM = \Delta EFM\) suy ra \(\widehat {EMD} = \widehat {EMF}\) (hai góc tương ứng)
Mà \(\widehat {EMD}\) và \(\widehat {EMF}\) là hai góc kề bù nên \(\widehat {EMD} + \widehat {EMF} = {180^0}\)
Suy ra \(\widehat {EMD} = \widehat {EMF} = \frac{{{{180}^0}}}{2} = {90^0}\) hay \(EM \bot DF\) (đpcm)
c) \(\Delta EDM = \Delta EFM\) suy ra \(\widehat {DEM} = \widehat {FEM}\) (hai góc tương ứng)
Xét \(\Delta AEM\) và \(\Delta BEM\) có:
\(\widehat {AEM} = \widehat {BEM}\) (cmt)
\(\widehat {EAM} = \widehat {EBM}\left( { = {{90}^0}} \right)\)
EM chung
Suy ra \(\Delta AEM = \Delta BEM\) (cạnh huyền – góc nhọn)
Suy ra AE = EB (hai cạnh tương ứng) suy ra \(\Delta AEB\) là tam giác cân tại E.
\(\widehat {EAB} = \widehat {EBA} = \frac{{{{180}^0} - \widehat E}}{2}\)
Mà \(\Delta DFE\) cân tại E nên \(\widehat {EDF} = \widehat {EFD} = \frac{{{{180}^0} - \widehat E}}{2}\)
Suy ra \(\widehat {EAB} = \widehat {EDF}\).
Mà \(\widehat {EAB}\) và \(\widehat {EDF}\) là hai góc đồng vị nên AB // DF (đpcm)
Cho ba số a, b, c khác 0 thỏa mãn: \(\frac{{ab}}{{a + b}} = \frac{{bc}}{{b + c}} = \frac{{ca}}{{c + a}}\).
Tính giá trị của biểu thức \(M = \frac{{2ab + 3bc + ca}}{{2{a^2} + 3{b^2} + {c^2}}}\).
Biến đổi \(\frac{{ab}}{{a + b}} = \frac{{bc}}{{b + c}} = \frac{{ca}}{{c + a}}\) thành \(\frac{{a + b}}{{ab}} = \frac{{b + c}}{{bc}} = \frac{{a + c}}{{ac}}\) và rút gọn để tìm a, b, c.
Thay a, b, c vào M để tính giá trị của M.
Ta có:\(\frac{{ab}}{{a + b}} = \frac{{bc}}{{b + c}} = \frac{{ac}}{{a + c}}\)
\(\frac{{a + b}}{{ab}} = \frac{{b + c}}{{bc}} = \frac{{a + c}}{{ac}}\)
\(\frac{a}{{ab}} + \frac{b}{{ab}} = \frac{b}{{bc}} + \frac{c}{{bc}} = \frac{a}{{ac}} + \frac{c}{{ac}}\)
suy ra \(\frac{1}{a} + \frac{1}{b} = \frac{1}{b} + \frac{1}{c} = \frac{1}{a} + \frac{1}{c}\)
Ta có \(\frac{1}{a} + \frac{1}{b} = \frac{1}{b} + \frac{1}{c}\)
\(\frac{1}{a} = \frac{1}{c}\) suy ra \(a = c\) (1)
\(\frac{1}{b} + \frac{1}{c} = \frac{1}{a} + \frac{1}{c}\)
\(\frac{1}{a} = \frac{1}{b}\) suy ra \(a = b\) (2)
Từ (1) và (2) suy ra a = b = c
Thay vào M, ta được:
\(\begin{array}{l}M = \frac{{2ab + 3bc + ca}}{{2{a^2} + 3{b^2} + {c^2}}}\\M = \frac{{2.a.a + 3.a.a + a.a}}{{2{a^2} + 3{a^2} + {a^2}}}\\M = \frac{{6{a^2}}}{{6{a^2}}} = 1\end{array}\)
Vậy M = 1.
Đề thi giữa kì 2 Toán 7 Chân trời sáng tạo - Đề số 10 đóng vai trò quan trọng trong việc đánh giá mức độ nắm vững kiến thức của học sinh sau một nửa học kì. Đề thi này không chỉ kiểm tra khả năng vận dụng công thức, định lý mà còn đánh giá tư duy logic và kỹ năng giải quyết vấn đề của học sinh. Bài viết này sẽ cung cấp một cái nhìn tổng quan về đề thi, phân tích các dạng bài tập thường gặp và hướng dẫn giải chi tiết một số câu hỏi điển hình.
Thông thường, đề thi giữa kì 2 Toán 7 Chân trời sáng tạo - Đề số 10 sẽ bao gồm các phần sau:
Ví dụ 1: Giải phương trình 2x + 5 = 11
Lời giải:
Ví dụ 2: Cho tam giác ABC có góc A = 60 độ, góc B = 80 độ. Tính góc C.
Lời giải:
Tổng ba góc trong một tam giác bằng 180 độ. Do đó, góc C = 180 độ - góc A - góc B = 180 độ - 60 độ - 80 độ = 40 độ.
Đề thi giữa kì 2 Toán 7 Chân trời sáng tạo - Đề số 10 là cơ hội để học sinh đánh giá năng lực và củng cố kiến thức. Bằng cách nắm vững kiến thức cơ bản, luyện tập thường xuyên và áp dụng các mẹo học tập hiệu quả, các em có thể tự tin đạt kết quả tốt nhất trong kỳ thi sắp tới. Chúc các em học tốt!