Chào mừng các em học sinh lớp 7 đến với đề thi học kì 2 môn Toán, đề số 11, chương trình Chân trời sáng tạo.
Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong học kì.
Hãy làm bài một cách cẩn thận và tự tin để đạt kết quả tốt nhất nhé!
Hai đại lượng x, y trong công thức nào tỉ lệ nghịch với nhau:
Gieo một con xúc xắc được chế tạo cân đối. Biến cố “Số chấm xuất hiện trên con xúc xắc là 5” là biến cố:
Chọn ngẫu nhiên 1 số trong 4 số sau: 7; 8; 26; 101. Xác xuất để chọn được số chia hết cho 5 là:
Cho hai đa thức f(x) = 5x4 + x3 – x2 + 1 và g(x) = –5x4 – x2 + 2.
Tính h(x) = f(x) + g(x) và tìm bậc của h(x). Ta được:
Sắp xếp đa thức 6x3 + 5x4 – 8x6 – 3x2 + 4 theo lũy thừa giảm dần của biến ta được:
Cho ΔABC có AC > BC > AB. Trong các khẳng định sau, câu nào đúng?
Hãy chọn cụm từ thích hợp điền vào chỗ trống: "Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào có hình chiếu nhỏ hơn thì ..."
Cho ΔABC có: \(\widehat A = 3{5^0}\). Đường trung trực của AC cắt AB ở D. Biết CD là tia phân giác của \(\widehat {ACB} \). Số đo các góc \(\widehat {ABC}; \widehat {ACB} \)là:
Cho hình vẽ sau.
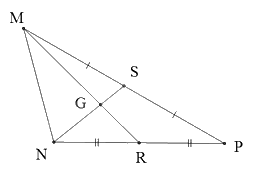
Biết MG = 3cm. Độ dài đoạn thẳng MR bằng:
Cho tam giác MNP có NP = 1cm, MP = 7cm. Độ dài cạnh MN là một số nguyên (cm). Độ dài cạnh MN là:
Cho tam giác ABC có AB = AC. Trên các cạnh AB và AC lấy các điểm D, E sao cho \(AD = AE\). Gọi K là giao điểm của BE và CD. Chọn câu sai
Giao điểm của ba đường trung trực của tam giác
Tìm x trong các tỉ lệ thức sau:
a) x : 27 = –2 : 3,6
b) \(\frac{{2x + 1}}{{-27}} = \frac{{- 3}}{{2x + 1}}\)
Cho đa thức \(Q(x) = - 3{x^4} + 4{x^3} + 2{x^2} + \frac{2}{3} - 3x - 2{x^4} - 4{x^3} + 8{x^4} + 1 + 3x\)
a) Thu gọn và sắp xếp theo lũy thừa giảm dần của biến.
b) Chứng tỏ Q(x) không có nghiệm.
Chọn ngẫu nhiên một số trong bốn số 11;12;13 và 14. Tìm xác suất để:
a) Chọn được số chia hết cho 5
b) Chọn được số có hai chữ số
c) Chọn được số nguyên tố
d) Chọn được số chia hết cho 6
Cho \(\Delta MNP\)cân tại M \(\left( {\widehat M < {{90}^0}} \right)\). Kẻ NH \( \bot \)MP \(\left( {H \in MP} \right)\), PK \( \bot \)MN \(\left( {K \in MN} \right)\). NH và PK cắt nhau tại E.
a) Chứng minh \(\Delta NHP = \Delta PKN\)
b) Chứng minh \(\Delta \)ENP cân.
c) Chứng minh ME là đường phân giác của góc NMP.
Cho đa thức bậc hai P(x) = ax2 + bx + c. Trong đó: a,b và c là những số với a ≠ 0. Cho biết a + b + c = 0. Giải thích tại sao x = 1 là một nghiệm của P(x)
Cho x; y; z tỉ lệ thuận với 3; 4; 5. Tính giá trị của biểu thức
\(A = 2024\left( {x - y} \right)\left( {y - z} \right) - 506{\left( {\frac{{x + y + z}}{6}} \right)^2}\)
Hai đại lượng x, y trong công thức nào tỉ lệ nghịch với nhau:
Đáp án : B
Dựa vào kiến thức về hai đại lượng tỉ lệ nghịch.
Vì x và y tỉ lệ nghịch với nhau nên ta có \(x.y = 5\) hay \(x = \frac{5}{y}\).
Đáp án B.
Gieo một con xúc xắc được chế tạo cân đối. Biến cố “Số chấm xuất hiện trên con xúc xắc là 5” là biến cố:
Đáp án : C
Dựa vào kiến thức về biến cố.
Biến cố “Số chấm xuất hiện trên con xúc xắc là 5” là biến cố ngẫu nhiên.
Đáp án C.
Chọn ngẫu nhiên 1 số trong 4 số sau: 7; 8; 26; 101. Xác xuất để chọn được số chia hết cho 5 là:
Đáp án : A
Xác định khả năng xuất hiện của biến cố.
Trong 4 số trên, không có số nào chia hết cho 5. Do đó xác suất để chọn được số chia hết cho 5 là 0.
Đáp án A.
Cho hai đa thức f(x) = 5x4 + x3 – x2 + 1 và g(x) = –5x4 – x2 + 2.
Tính h(x) = f(x) + g(x) và tìm bậc của h(x). Ta được:
Đáp án : B
Sử dụng quy tắc cộng hai đa thức
h(x) = f(x) + g(x)
= (5x4 + x3 – x2 + 1) + (–5x4 – x2 + 2)
= 5x4 + x3 – x2 + 1 – 5x4 – x2 + 2
= (5x4 – 5x4) + x3 + (- x2 – x2) + (1 + 2)
= x3 – 2x2 + 3
Bậc của h(x) là 3.
Đáp án B.
Sắp xếp đa thức 6x3 + 5x4 – 8x6 – 3x2 + 4 theo lũy thừa giảm dần của biến ta được:
Đáp án : D
Dựa vào kiến thức về đa thức một biến.
6x3 + 5x4 – 8x6 – 3x2 + 4 = - 8x6 + 5x4 + 6x3 – 3x2 + 4
Đáp án D.
Cho ΔABC có AC > BC > AB. Trong các khẳng định sau, câu nào đúng?
Đáp án : C
Dựa vào quan hệ giữa góc và cạnh đối diện trong tam giác.
Vì AC > BC > AB nên \(\widehat B > \widehat A > \widehat C\) hay \(\widehat C < \widehat A < \widehat B\).
Đáp án C.
Hãy chọn cụm từ thích hợp điền vào chỗ trống: "Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào có hình chiếu nhỏ hơn thì ..."
Đáp án : C
Dựa vào kiến thức về đường xiên.
"Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào có hình chiếu nhỏ hơn thì nhỏ hơn".
Đáp án C.
Cho ΔABC có: \(\widehat A = 3{5^0}\). Đường trung trực của AC cắt AB ở D. Biết CD là tia phân giác của \(\widehat {ACB} \). Số đo các góc \(\widehat {ABC}; \widehat {ACB} \)là:
Đáp án : C
Dựa vào đặc điểm của đường trung trực.
Sử dụng định lí tổng ba góc của một tam giác bằng \({180^0}\)
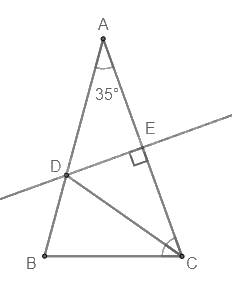
Đường trung trực của AC đi qua điểm D nên tam giác ADC cân tại D.
Do đó \(\widehat {DAC} = \widehat {DCA} = {35^0}\).
Mà CD là tia phân giác của \(\widehat {ACB}\) nên \(\widehat {ACB} = 2\widehat {DCA} = {2.35^0} = {70^0}\)
Từ đó suy ra:
\(\begin{array}{l}\widehat {ABC} = {180^0} - \widehat {BAC} - \widehat {BCA}\\ = {180^0} - {35^0} - {70^0} = {75^0}\end{array}\)
Vậy \(\widehat {ABC} = 7{5^0}; \widehat {ACB} = 7{0^0}\).
Đáp án C.
Cho hình vẽ sau.
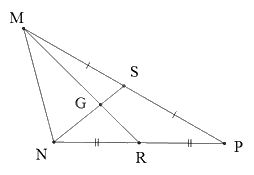
Biết MG = 3cm. Độ dài đoạn thẳng MR bằng:
Đáp án : A
Chứng minh MR là đường trung tuyến nên G là trọng tâm của tam giác để tính MR.
Vì S là trung điểm của MP và R là trung điểm của NP nên MR và NS là hai đường trung tuyến của tam giác MNP.
MR và NS cắt nhau tại G nên G là trọng tâm của tam giác MNP.
Do đó \(MG = \frac{2}{3}MR\) suy ra \(MR = MG:\frac{2}{3} = 3:\frac{2}{3} = \frac{9}{2} = 4,5\left( {cm} \right)\)
Đáp án A.
Cho tam giác MNP có NP = 1cm, MP = 7cm. Độ dài cạnh MN là một số nguyên (cm). Độ dài cạnh MN là:
Đáp án : D
Dựa vào bất đẳng thức tam giác để tính độ dài MN.
Vì NP, MP và MN là độ dài 3 cạnh của một tam giác nên ta có:
\(\begin{array}{l}MP - NP < MN < MP + NP\\7 - 1 < MN < 7 + 1\\6 < MN < 8\end{array}\)
Mà MN là số nguyên nên MN chỉ có thể bằng 7cm.
Đáp án D.
Cho tam giác ABC có AB = AC. Trên các cạnh AB và AC lấy các điểm D, E sao cho \(AD = AE\). Gọi K là giao điểm của BE và CD. Chọn câu sai
Đáp án : D
Chứng minh các \(\Delta ABE = \Delta ACD\) và \(\Delta BKC\) cân để kiểm tra.
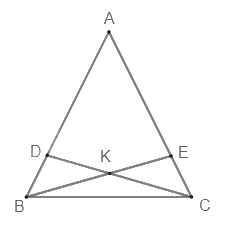
Xét tam giác ABE và ACD có:
AB = AC (gt)
\(\widehat {BAC}\) chung
AE = AD (gt)
suy ra \(\Delta ABE = \Delta ACD\left( {c.g.c} \right)\)
suy ra BE = CD (hai cạnh tương ứng nên A đúng.
và \(\widehat {ABE} = \widehat {ACD}\) (hai góc tương ứng)
Mà \(\widehat {ABC} = \widehat {ACB}\) (tam giác ABC cân tại A vì AB = AC)
Suy ra \(\widehat {KBC} = \widehat {KCB}\) nên \(\Delta BKC\) cân tại K.
Do đó BK = CK nên B đúng.
Vì AB = AC, AD = AE nên AB – AD = AC – AE hay BD = CE nên C đúng.
Ta chưa đủ điều kiện có DK = KC nên đáp án D sai.
Đáp án D.
Giao điểm của ba đường trung trực của tam giác
Đáp án : C
Dựa vào kiến thức giao điểm của ba đường trung trực.
Giao điểm của ba đường trung trực của tam giác cách đều ba đỉnh của tam giác nên C đúng.
Đáp án C.
Tìm x trong các tỉ lệ thức sau:
a) x : 27 = –2 : 3,6
b) \(\frac{{2x + 1}}{{-27}} = \frac{{- 3}}{{2x + 1}}\)
Dựa vào kiến thức về tỉ lệ thức:
+ Nếu \(\frac{a}{b} = \frac{c}{d}\) thì \(ad = bc\).
+ Nếu \(ad = bc\) (với \(a,b,c,d \ne 0\)) thì ta có các tỉ lệ thức:
\(\frac{a}{b} = \frac{c}{d};\frac{a}{c} = \frac{b}{d};\frac{b}{a} = \frac{d}{c};\frac{c}{a} = \frac{d}{b}\).
a) \(x:27 = -2:3,6\)
\(\begin{array}{l}\frac{x}{{27}} = \frac{{- 5}}{9}\\x = \frac{{- 5.27}}{9}\\x = -15\end{array}\)
Vậy \(x = -15\).
b) \(\frac{{2x + 1}}{{-27}} = \frac{{- 3}}{{2x + 1}}\)
\(\begin{array}{l}{\left( {2x + 1} \right)^2} = 81\\{\left( {2x + 1} \right)^2} = {9^2}\\\left[ \begin{array}{l}2x + 1 = 9\\2x + 1 = -9\end{array} \right.\\\left[ \begin{array}{l}2x = 8\\2x = -10\end{array} \right.\\\left[ \begin{array}{l}x = 4\\x = -5\end{array} \right.\end{array}\)
Vậy \(x = 4\) hoặc \(x = - 5\).
Cho đa thức \(Q(x) = - 3{x^4} + 4{x^3} + 2{x^2} + \frac{2}{3} - 3x - 2{x^4} - 4{x^3} + 8{x^4} + 1 + 3x\)
a) Thu gọn và sắp xếp theo lũy thừa giảm dần của biến.
b) Chứng tỏ Q(x) không có nghiệm.
a) Sử dụng quy tắc thu gọn đa thức một biến.
b) Chứng minh Q(x) không thể bằng 0.
a)
\(\begin{array}{l}Q(x) = - 3{x^4} + 4{x^3} + 2{x^2} + \frac{2}{3} - 3x - 2{x^4} - 4{x^3} + 8{x^4} + 1 + 3x\\ = \left( { - 3{x^4} - 2{x^4} + 8{x^4}} \right) + \left( {4{x^3} - 4{x^3}} \right) + 2{x^2} + \left( {3x - 3x} \right) + \left( {\frac{2}{3} + 1} \right)\\ = 3{x^4} + 2{x^2} + \frac{5}{3}\end{array}\)
b) Ta có:
\({x^4} \ge 0\) với mọi giá trị \(x\)
\(3{x^4} \ge 0\) với mọi giá trị \(x\)
\({x^2} \ge 0\) với mọi giá trị \(x\)
\((2{x^2} \ge 0\) với mọi giá trị \(x\)
\(Q(x) = 3{x^4} + 2{x^2} + \frac{5}{3} \ge \frac{5}{3}\) với mọi giá trị \(x\)
Vậy \(Q\left( x \right)\) không có nghiệm
Chọn ngẫu nhiên một số trong bốn số 11;12;13 và 14. Tìm xác suất để:
a) Chọn được số chia hết cho 5
b) Chọn được số có hai chữ số
c) Chọn được số nguyên tố
d) Chọn được số chia hết cho 6
Kiểm tra khả năng xảy ra của biến cố.
a) Không có số nào chia hết cho 5 nên xác suất để chọn được số chia hết cho 5 là 0.
b) Cả 4 số đều là số có hai chữ số nên xác suất để chọn được số có hai chữ số là 1.
c) Có hai số (11; 13) là số nguyên tố nên xác suất để chọn được số nguyên tố là \(\frac{2}{4} = \frac{1}{2}\).
d) Có một số (12) chia hết cho 6 nên xác suất để chọn được số chia hết cho 6 là \(\frac{1}{4}\).
Cho \(\Delta MNP\)cân tại M \(\left( {\widehat M < {{90}^0}} \right)\). Kẻ NH \( \bot \)MP \(\left( {H \in MP} \right)\), PK \( \bot \)MN \(\left( {K \in MN} \right)\). NH và PK cắt nhau tại E.
a) Chứng minh \(\Delta NHP = \Delta PKN\)
b) Chứng minh \(\Delta \)ENP cân.
c) Chứng minh ME là đường phân giác của góc NMP.
a) Chứng minh \(\Delta NHP = \Delta PKN\) theo trường hợp cạnh huyền – góc nhọn.
b) Chứng minh \(\widehat {{P_1}} = \widehat {{N_1}}\) nên \(\Delta ENP\) cân.
c) Chứng minh MK = MH.
Chứng minh \(\Delta MEK = \Delta MEH\) (cạnh huyền – cạnh góc vuông) suy ra \(\widehat {{M_1}} = \widehat {{M_2}}\).
Do đó ME là đường phân giác của góc NMP.
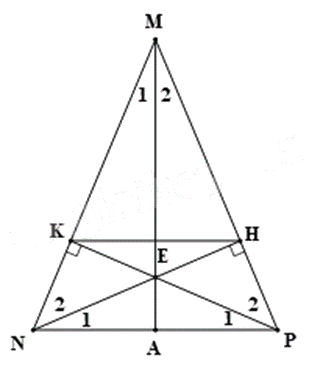
a) Xét \(\Delta NHP\) và \(\Delta PKN\) vuông tại H và K có:
\(\widehat {NPH} = \widehat {PNK}\) (vì \(\Delta MNP\) cân tại M)
\(NP\) chung
Suy ra \(\Delta NHP = \Delta PKN\) (cạnh huyền – góc nhọn) (đpcm)
b) Vì \(\Delta NHP = \Delta PKN\)nên \(\widehat {{N_1}} = \widehat {{P_1}}\).
Do đó \(\Delta ENP\) cân tại E (đpcm)
c) Ta có:
\(MK = MN - NK\) (vì K thuộc MN)
\(MH = MP - HP\) (vì H thuộc MP)
Mà \(MN = MP\) (vì \(\Delta MNP\) cân tại M)
\(NK = PH\) (vì \(\Delta NHP = \Delta PKN\))
suy ra \(MK = MH\).
Xét \(\Delta MEK\) và \(\Delta MEH\) vuông tại K và H có:
ME là cạnh chung
MK = MH (cmt)
Suy ra \(\Delta MEK = \Delta MEH\) (ch – cgv)
Suy ra \(\widehat {{M_1}} = \widehat {{M_2}}\) suy ra ME là tia phân giác của góc NMP (đpcm)
Cho đa thức bậc hai P(x) = ax2 + bx + c. Trong đó: a,b và c là những số với a ≠ 0. Cho biết a + b + c = 0. Giải thích tại sao x = 1 là một nghiệm của P(x)
Thay x = 1 vào đa thức P(x) để giải thích.
Thay x = 1 vào đa thức P(x), ta có:
P(1) = a.12 + b.1 + c = a + b + c
Mà a + b + c = 0
Do đó, P(1) = 0.
Như vậy x = 1 là một nghiệm của P(x)
Cho x; y; z tỉ lệ thuận với 3; 4; 5. Tính giá trị của biểu thức
\(A = 2024\left( {x - y} \right)\left( {y - z} \right) - 506{\left( {\frac{{x + y + z}}{6}} \right)^2}\)
Viết tỉ lệ thức của x; y; z.
Đặt tỉ lệ đó bằng k, biểu diễn x; y; z theo k.
Thay vào A, tính giá trị của A theo k.
Vì x; y; z tỉ lệ thuận với 3; 4; 5 nên \(\frac{x}{3} = \frac{y}{4} = \frac{z}{5}\).
Đặt \(\frac{x}{3} = \frac{y}{4} = \frac{z}{5} = k\) ta được:
\(x = 3k;y = 4k;z = 5k\).
Khi đó,
\(\begin{array}{l}A = 2024\left( {3k - 4k} \right)\left( {4k - 5k} \right) - 506{\left( {\frac{{3k + 4k + 5k}}{6}} \right)^2}\\ = 2024\left( { - k} \right)\left( { - k} \right) - 506{\left( {2k} \right)^2}\\ = 2024{k^2} - 2024{k^2}\\ = 0\end{array}\)
Vậy A = 0.
Đề thi học kì 2 Toán 7 - Đề số 11, chương trình Chân trời sáng tạo, là một bài kiểm tra quan trọng giúp học sinh đánh giá mức độ nắm vững kiến thức và kỹ năng đã học trong suốt học kì. Đề thi bao gồm nhiều dạng bài tập khác nhau, từ trắc nghiệm đến tự luận, đòi hỏi học sinh phải có sự hiểu biết sâu sắc về các khái niệm và công thức toán học.
Đề thi thường được chia thành các phần chính sau:
Đề thi học kì 2 Toán 7 - Đề số 11 thường tập trung vào các chủ đề sau:
Để giải phương trình bậc nhất một ẩn, ta thực hiện các bước sau:
Để chứng minh hai tam giác bằng nhau, ta sử dụng các trường hợp bằng nhau của tam giác:
Để chuẩn bị tốt nhất cho kỳ thi học kì 2, các em có thể tham khảo các tài liệu sau:
Đề thi học kì 2 Toán 7 - Đề số 11 - Chân trời sáng tạo là một cơ hội để các em thể hiện những kiến thức và kỹ năng đã học. Hãy tự tin và cố gắng hết mình để đạt kết quả tốt nhất nhé!