Chào mừng các em học sinh lớp 7 đến với đề thi giữa kì 1 Toán 7 - Đề số 12 của giaitoan.edu.vn. Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong giai đoạn giữa kì 1.
Đề thi bao gồm các dạng bài tập khác nhau, từ cơ bản đến nâng cao, giúp các em làm quen với nhiều dạng câu hỏi thường gặp trong các bài kiểm tra.
Trong các số \( - \frac{1}{3};\,\,0;\,\,1,5;\,\, - \left( {\frac{{ - 1}}{2}} \right)\), các số hữu tỉ âm là:
\(1,5;\,\,0\).
\( - \frac{1}{3}\).
\( - \frac{1}{3};\,\, - \left( {\frac{{ - 1}}{2}} \right)\).
\( - \left( {\frac{{ - 1}}{2}} \right)\).
Số đối của số hữu tỉ \( - 2\frac{3}{5}\) dưới dạng phân số là:
\(2\frac{3}{5}\).
\(\frac{{ - 13}}{5}\).
\(\frac{{13}}{5}\).
\( - 2,6\).
Chọn khẳng định đúng trong các khẳng định sau.
Số hữu tỉ âm nhỏ hơn số hữu tỉ dương.
Số 0 là số hữu tỉ dương.
Số nguyên âm không phải là số hữu tỉ âm.
Tập hợp \(\mathbb{Q}\) gồm các số hữu tỉ dương và các số hữu tỉ âm.
Cho số hữu tỉ \(x\). Chọn khẳng định đúng?
\({x^m}.{x^n} = {x^{m.n}}\).
\({\left( {x.y} \right)^n} = {x^n} + {y^n}\).
\({x^m}:{x^n} = {x^{m - n}} \left( {x \ne 0;\,\,m \ge n} \right)\).
\({\left( {{x^m}} \right)^n} = {x^{m + n}}\).
Cho \(A = \frac{3}{{n - 2}}\). Tìm điều kiện của số nguyên n để A là một số hữu tỉ.
\(n > 2\).
\(n < 2\).
\(n = 2\).
\(n \ne 2\).
Phát biểu nào sau đây đúng về hình lập phương \(ABCD.MNPQ\).
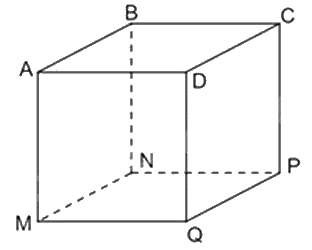
Bốn đường chéo \(AP,\,BP,\,CM,\,DB\).
Ba góc vuông ở đỉnh A: góc \(DAB\), góc \(DAM\), góc \(MAB\).
\(AM = AB = AD = AC\).
Bốn mặt bên là \(ABCD\), \(MNPQ\), \(AMNB\),\(BNPC\).
Cho các hình vẽ sau. Hình nào có dạng hình lăng trụ đứng?

Hình 1 và Hình 2.
Hình 2 và Hình 3.
Hình 3.
Tất cả các hình trên.
Diện tích xung quanh của hình hộp chữ nhật có độ dài hai đáy là \(6\,cm;\,\,8\,cm\) và chiều cao \(10\,cm\) là:
\(6.8.10\,\left( {c{m^2}} \right)\).
\(\left( {6 + 8} \right).10\,\left( {c{m^2}} \right)\).
\(6 + 8 + 10\,\left( {c{m^2}} \right)\).
\(2.\left( {6 + 8} \right).10\,\left( {c{m^2}} \right)\).
Cho lăng trụ đứng tam giác \(ABC.DEF\). Các mặt bên của lăng trụ là
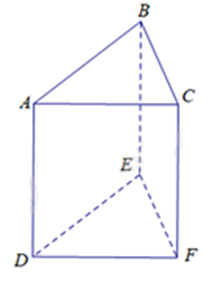
\(ABC;{\rm{ }}DEF\).
\(ABC;{\rm{ }}DEF;{\rm{ }}ACFD\).
\(ABED;{\rm{ }}BCFE\).
\(ABED;{\rm{ }}BCFE;{\rm{ }}ACFD\).
Cho hình lăng trụ đứng có chu vi đáy, diện tích đáy và chiều cao lần lượt là \(C,S,h\). Khẳng định đúng là
\({S_{xq}} = C.h\).
\(V = C.S\).
\(V = C.h\).
\({S_{xq}} = \frac{V}{h}\).
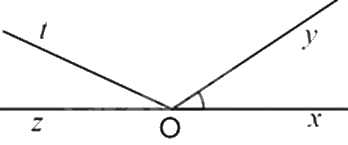
Cho hình vẽ sau. Góc kề bù với góc \(xOy\) là:
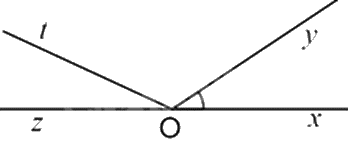
\(\widehat {zOy}\).
\(\widehat {tOy}\).
\(\widehat {tOz}\).
\(\widehat {xOt}\).
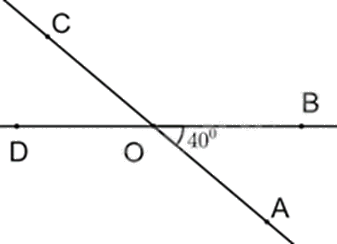
Góc COD có số đo bằng bao nhiêu độ?
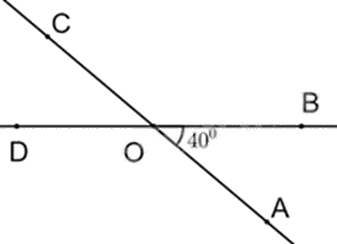
\(140^\circ \).
\(90^\circ \).
\(50^\circ \).
\(40^\circ \).
Thực hiện phép tính (tính hợp lý nếu có thể):
a) \(\frac{7}{3} + \frac{{ - 8}}{{12}} + \frac{5}{4}.\)
b) \({\left( {\frac{{ - 2}}{3}} \right)^2}.\frac{{67}}{4} + \frac{{ - 7}}{4}.{\left( {\frac{{ - 2}}{3}} \right)^2}.\)
c) \(\left( {\frac{6}{{23}} - \frac{6}{{33}}} \right) - \left( {\frac{{27}}{{33}} - \frac{{17}}{{23}}} \right) + 2\frac{4}{7}.\)
Tìm \(x\), biết:
a) \(\frac{6}{7} - x = \frac{{12}}{{28}}.\)
b) \(\frac{{ - 5}}{3} + \frac{7}{{10}}x = 0,2.\)
c) \({\left( {2x + 6} \right)^2} = \frac{{81}}{{25}}.\)
Cho hình vẽ bên.
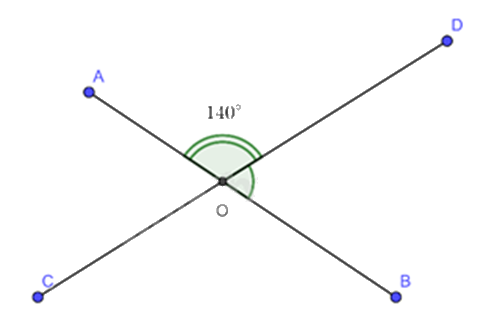
Tính \(\widehat {DOB}\) biết \(\widehat {AOD} = 140^\circ \).
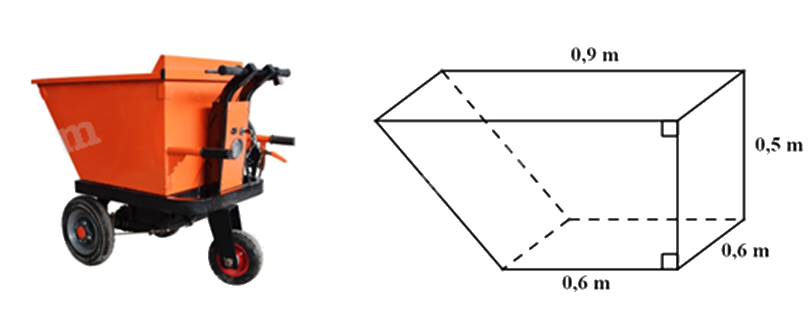
Thùng của một xe rùa điện có dạng hình lăng trụ đứng tứ giác; mặt đáy của hình lăng trụ này là một hình thang vuông có độ dài đáy lớn, đáy nhỏ và chiều cao lần lượt là \(0,9m\); \(0,6m\) và \(0,5m\), chiều cao của hình lăng trụ là \(0,6m\) (xem hình vẽ bên dưới). Để đảm bảo an toàn cho bác công nhân chở cát, mỗi chuyến xe chỉ vận chuyển được \(96\% \) thể tích của thùng xe. Hỏi bác công nhân phải vận chuyển ít nhất bao nhiêu chuyến xe để chở hết \(54{m^3}\) cát?
Một cửa hàng điện tử nhập về lô hàng gồm 50 chiếc điện thoại, giá tiền của một chiếc điện thoại khi nhập về là 10 000 000 đồng. Sau khi đã bán được 40 chiếc điện thoại với giá bằng \(120\% \)giá vốn mua ban đầu thì lượng khách hàng mua sản phẩm giảm xuống nên cửa hàng đã thực hiện chương trình giảm giá đặc biệt dành cho 10 chiếc điện thoại cuối cùng để thu hút khách hàng. Hỏi sau khi bán hết lô hàng trên, cửa hàng kỳ vọng lãi được 70 000 000 đồng thì phải giảm giá bao nhiêu phần trăm cho 10 chiếc điện thoại cuối cùng so với giá bán 40 chiếc điện thoại trước đó.
Trong các số \( - \frac{1}{3};\,\,0;\,\,1,5;\,\, - \left( {\frac{{ - 1}}{2}} \right)\), các số hữu tỉ âm là:
\(1,5;\,\,0\).
\( - \frac{1}{3}\).
\( - \frac{1}{3};\,\, - \left( {\frac{{ - 1}}{2}} \right)\).
\( - \left( {\frac{{ - 1}}{2}} \right)\).
Đáp án : B
Số hữu tỉ âm là các số hữu tỉ nhỏ hơn 0.
Có 1 số hữu tỉ âm là: \( - \frac{1}{3}\).
Đáp án B.
Số đối của số hữu tỉ \( - 2\frac{3}{5}\) dưới dạng phân số là:
\(2\frac{3}{5}\).
\(\frac{{ - 13}}{5}\).
\(\frac{{13}}{5}\).
\( - 2,6\).
Đáp án : C
Số đối của số hữu tỉ a là – a.
Ta có: \( - 2\frac{3}{5} = - \frac{{13}}{5}\) nên số đối của \( - 2\frac{3}{5}\) là \( - \left( { - \frac{{13}}{5}} \right) = \frac{{13}}{5}\).
Đáp án C.
Chọn khẳng định đúng trong các khẳng định sau.
Số hữu tỉ âm nhỏ hơn số hữu tỉ dương.
Số 0 là số hữu tỉ dương.
Số nguyên âm không phải là số hữu tỉ âm.
Tập hợp \(\mathbb{Q}\) gồm các số hữu tỉ dương và các số hữu tỉ âm.
Đáp án : A
Dựa vào kiến thức về số hữu tỉ.
Số hữu tỉ âm nhỏ hơn số hữu tỉ dương nên A đúng.
Số 0 không phải số hữu tỉ âm cũng không phải số hữu tỉ dương nên B sai.
Số nguyên âm cũng là số hữu tỉ âm nên C sai.
Tập hợp \(\mathbb{Q}\) gồm các số hữu tỉ dương, các số hữu tỉ âm và số 0 nên D sai.
Đáp án A.
Cho số hữu tỉ \(x\). Chọn khẳng định đúng?
\({x^m}.{x^n} = {x^{m.n}}\).
\({\left( {x.y} \right)^n} = {x^n} + {y^n}\).
\({x^m}:{x^n} = {x^{m - n}} \left( {x \ne 0;\,\,m \ge n} \right)\).
\({\left( {{x^m}} \right)^n} = {x^{m + n}}\).
Đáp án : C
Dựa vào kiến thức về lũy thừa với số mũ tự nhiên.
Ta có:
+) \({x^m}.{x^n} = {x^{m + n}}\) nên A sai.
+) \({\left( {x.y} \right)^n} = {x^n}.{y^n}\) nên B sai.
+) \({x^m}:{x^n} = {x^{m - n}} \left( {x \ne 0;\,\,m \ge n} \right)\) nên khẳng định C đúng.
+) \({\left( {{x^m}} \right)^n} = {x^{m.n}}\) nên khẳng định D sai.
Đáp án C.
Cho \(A = \frac{3}{{n - 2}}\). Tìm điều kiện của số nguyên n để A là một số hữu tỉ.
\(n > 2\).
\(n < 2\).
\(n = 2\).
\(n \ne 2\).
Đáp án : D
Một số là số hữu tỉ thì mẫu số của số đó khác 0.
Để A là một số hữu tỉ thì \(n - 2 \ne 0\) suy ra \(n \ne 2\).
Đáp án D.
Phát biểu nào sau đây đúng về hình lập phương \(ABCD.MNPQ\).
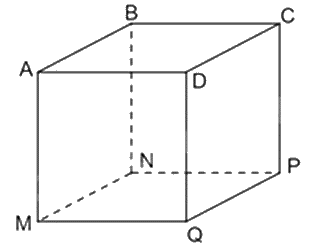
Bốn đường chéo \(AP,\,BP,\,CM,\,DB\).
Ba góc vuông ở đỉnh A: góc \(DAB\), góc \(DAM\), góc \(MAB\).
\(AM = AB = AD = AC\).
Bốn mặt bên là \(ABCD\), \(MNPQ\), \(AMNB\),\(BNPC\).
Đáp án : B
Dựa vào đặc điểm của hình lập phương.
Các đường chéo của hình lập phương là \(AP,BQ,CM,DN\) nên A sai.
Ba góc vuông ở đỉnh A là: góc \(DAB\), góc \(DAM\), góc \(MAB\) nên B đúng.
Vì ABCD.MNPQ là hình lập phương nên \(AM = AB = AD\). AC là đường chéo của ABCD nên AC không bằng AM. Do đó khẳng định C sai.
Bốn mặt bên của hình lập phương là ABNM, BCPN, CDQP, ADQM nên khẳng định D sai.
Đáp án B.
Cho các hình vẽ sau. Hình nào có dạng hình lăng trụ đứng?

Hình 1 và Hình 2.
Hình 2 và Hình 3.
Hình 3.
Tất cả các hình trên.
Đáp án : D
Dựa vào kiến thức về hình lăng trụ đứng.
Hình hộp chữ nhật và hình lập phương cũng là hình lăng trụ đứng tứ giác.
Cả 3 hình đều là hình lăng trụ đứng, trong đó Hình 1 và Hình 2 là hình lăng trụ đứng tứ giác (hình hộp chữ nhật và hình lập phương cũng là hình lăng trụ đứng tứ giác); Hình 3 là hình lăng trụ đứng tam giác.
Đáp án D.
Diện tích xung quanh của hình hộp chữ nhật có độ dài hai đáy là \(6\,cm;\,\,8\,cm\) và chiều cao \(10\,cm\) là:
\(6.8.10\,\left( {c{m^2}} \right)\).
\(\left( {6 + 8} \right).10\,\left( {c{m^2}} \right)\).
\(6 + 8 + 10\,\left( {c{m^2}} \right)\).
\(2.\left( {6 + 8} \right).10\,\left( {c{m^2}} \right)\).
Đáp án : D
Sử dụng công thức tính diện tích xung quanh của hình hộp chữ nhật:
Sxq = Cđáy . h
Diện tích xung quanh của hình hộp chữ nhật là:
\({S_{xq}} = 2(6 + 8).10\left( {c{m^2}} \right)\).
Đáp án D.
Cho lăng trụ đứng tam giác \(ABC.DEF\). Các mặt bên của lăng trụ là
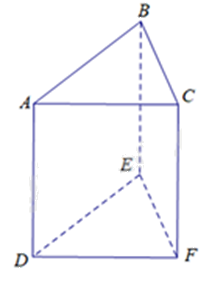
\(ABC;{\rm{ }}DEF\).
\(ABC;{\rm{ }}DEF;{\rm{ }}ACFD\).
\(ABED;{\rm{ }}BCFE\).
\(ABED;{\rm{ }}BCFE;{\rm{ }}ACFD\).
Đáp án : D
Dựa vào kiến thức về hình lăng trụ tam giác.
Các mặt bên của lăng trụ là: ABED, BCFE, ACFD.
Đáp án D.
Cho hình lăng trụ đứng có chu vi đáy, diện tích đáy và chiều cao lần lượt là \(C,S,h\). Khẳng định đúng là
\({S_{xq}} = C.h\).
\(V = C.S\).
\(V = C.h\).
\({S_{xq}} = \frac{V}{h}\).
Đáp án : A
Dựa vào công thức tính diện tích xung quanh và thể tích của hình lăng trụ.
Công thức tính diện tích xung quanh của hình lăng trụ đứng là: \({S_{xq}} = C.h\).
Thể tích của hình lăng trụ đứng là: \(V = S.h\).
Vậy đáp án đúng là A.
Đáp án A.
Cho hình vẽ sau. Góc kề bù với góc \(xOy\) là:
\(\widehat {zOy}\).
\(\widehat {tOy}\).
\(\widehat {tOz}\).
\(\widehat {xOt}\).
Đáp án : A
Dựa vào kiến thức về hai góc kề bù.
Góc kề bù với góc \(xOy\) là \(\widehat {zOy}\).
Đáp án A.
Góc COD có số đo bằng bao nhiêu độ?
\(140^\circ \).
\(90^\circ \).
\(50^\circ \).
\(40^\circ \).
Đáp án : D
Dựa vào kiến thức về hai góc đối đỉnh: hai góc đối đỉnh thì bằng nhau.
Vì \(\widehat {COD}\) và \(\widehat {AOB}\) là hai góc đối đỉnh nên \(\widehat {COD} = \widehat {AOB} = 40^\circ \).
Đáp án D.
Thực hiện phép tính (tính hợp lý nếu có thể):
a) \(\frac{7}{3} + \frac{{ - 8}}{{12}} + \frac{5}{4}.\)
b) \({\left( {\frac{{ - 2}}{3}} \right)^2}.\frac{{67}}{4} + \frac{{ - 7}}{4}.{\left( {\frac{{ - 2}}{3}} \right)^2}.\)
c) \(\left( {\frac{6}{{23}} - \frac{6}{{33}}} \right) - \left( {\frac{{27}}{{33}} - \frac{{17}}{{23}}} \right) + 2\frac{4}{7}.\)
Dựa vào quy tắc tính với số hữu tỉ, lũy thừa với số mũ tự nhiên.
a) \(\frac{7}{3} + \frac{{ - 8}}{{12}} + \frac{5}{4}\)
= \(\frac{{28}}{{12}} + \frac{{ - 8}}{{12}} + \frac{{15}}{{12}}\)
= \(\frac{{35}}{{12}}.\)
b) \({\left( {\frac{{ - 2}}{3}} \right)^2}.\frac{{67}}{4} + \frac{{ - 7}}{4}.{\left( {\frac{{ - 2}}{3}} \right)^2}\)
\( = {\left( {\frac{{ - 2}}{3}} \right)^2}.\left( {\frac{{67}}{4} + \frac{{ - 7}}{4}} \right)\)
\( = \frac{4}{9}.\frac{{60}}{4}\)\( = \frac{{60}}{9} = \frac{{20}}{3}.\)
c) \(\left( {\frac{6}{{23}} - \frac{6}{{33}}} \right) - \left( {\frac{{27}}{{33}} - \frac{{17}}{{23}}} \right) + 2\frac{4}{7}\)
\( = \frac{6}{{23}} - \frac{6}{{33}} - \frac{{27}}{{33}} + \frac{{17}}{{23}} + 2\frac{4}{7}\)
\( = \left( {\frac{6}{{23}} + \frac{{17}}{{23}}} \right) + \left( {\frac{{ - 6}}{{33}} + \frac{{ - 27}}{{33}}} \right) + 2\frac{4}{7}\)
\( = 1 + \left( { - 1} \right) + 2\frac{4}{7}\)\( = 2\frac{4}{7}\)
Tìm \(x\), biết:
a) \(\frac{6}{7} - x = \frac{{12}}{{28}}.\)
b) \(\frac{{ - 5}}{3} + \frac{7}{{10}}x = 0,2.\)
c) \({\left( {2x + 6} \right)^2} = \frac{{81}}{{25}}.\)
a), b) Chuyển vế để tìm x.
c) Với \({A^2} = {B^2}\), ta chia hai trường hợp: TH1: A = B; TH2: A = - B.
a) \(\frac{6}{7} - x = \frac{{12}}{{28}}\)
\(x = \frac{6}{7} - \frac{{12}}{{28}}\)
\(x = \frac{{24}}{{28}} - \frac{{12}}{{28}}\)
\(x = \frac{{12}}{{28}} = \frac{3}{7}\)
Vậy \(x = \frac{3}{7}\)
b) \(\frac{{ - 5}}{3} + \frac{7}{{10}}x = 0,2\)
\(\frac{7}{{10}}x = \frac{1}{5} + \frac{5}{3}\)
\(\frac{7}{{10}}x = \frac{3}{{15}} + \frac{{25}}{{15}} = \frac{{28}}{{15}}\)
\(x = \frac{{28}}{{15}}:\frac{7}{{10}}\)
\(x = \frac{8}{3}\)
Vậy \(x = \frac{8}{3}\)
c) \({\left( {2x + 6} \right)^2} = \frac{{81}}{{25}}\)
\({\left( {2x + 6} \right)^2} = {\left( {\frac{9}{5}} \right)^2} = {\left( {\frac{{ - 9}}{5}} \right)^2}.\)
* TH1: \(2x + 6 = \frac{9}{5}\)
\(2x = \frac{9}{5} - 6\)
\(2x = \frac{{ - 21}}{5}\)
\(x = \frac{{ - 21}}{5}:2\)
\(x = \frac{{ - 21}}{{10}}.\)
* TH2: \(2x + 6 = \frac{{ - 9}}{5}\)
\(2x = \frac{{ - 9}}{5} - 6\)
\(2x = \frac{{ - 39}}{5}\)
\(x = \frac{{ - 39}}{5}:2\)
\(x = \frac{{ - 39}}{{10}}.\)
Vậy \(x \in \left\{ {\frac{{ - 39}}{{10}};\frac{{ - 21}}{{10}}} \right\}\).
Cho hình vẽ bên.
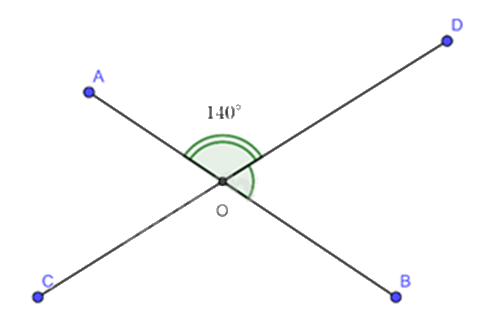
Tính \(\widehat {DOB}\) biết \(\widehat {AOD} = 140^\circ \).
Sử dụng kiến thức hai góc kề bù: Hai góc kề bù thì tổng của chúng bằng \(180^\circ \).
Vì \(\widehat {AOD}\) và \(\widehat {DOB}\) là 2 góc kề bù nên \(\widehat {AOD} + \widehat {DOB} = 180^\circ \)
\(140^\circ + \widehat {DOB} = 180^\circ \)
\(\widehat {DOB} = 180^\circ - 140^\circ \)
\(\widehat {DOB} = 40^\circ .\)
Vậy \(\widehat {DOB} = 40^\circ .\)
Thùng của một xe rùa điện có dạng hình lăng trụ đứng tứ giác; mặt đáy của hình lăng trụ này là một hình thang vuông có độ dài đáy lớn, đáy nhỏ và chiều cao lần lượt là \(0,9m\); \(0,6m\) và \(0,5m\), chiều cao của hình lăng trụ là \(0,6m\) (xem hình vẽ bên dưới). Để đảm bảo an toàn cho bác công nhân chở cát, mỗi chuyến xe chỉ vận chuyển được \(96\% \) thể tích của thùng xe. Hỏi bác công nhân phải vận chuyển ít nhất bao nhiêu chuyến xe để chở hết \(54{m^3}\) cát?
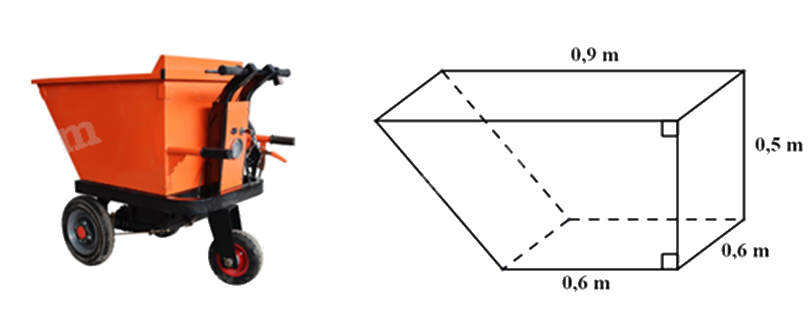
Sử dụng công thức tính thể tích hình lăng trụ đứng tứ giác.
Tính thể tích cát của mỗi chuyến xe.
Từ đó tính số chuyến xe ít nhất để vận chuyển hết cát.
Thể tích của thùng xe là:
\(\frac{{\left( {0,9 + 0,6} \right).0,5}}{2}.0,6 = 0,225\,\left( {{m^3}} \right)\)
Thể tích cát của mỗi chuyến xe là:
\(0,225.96\% = 0,216\,\left( {{m^3}} \right)\)
Ta có: \(54:0,216\, = 250\).
Vậy cần ít nhất 250 chuyến xe để có thể vận chuyển hết \(54\,{m^3}\) cát.
Một cửa hàng điện tử nhập về lô hàng gồm 50 chiếc điện thoại, giá tiền của một chiếc điện thoại khi nhập về là 10 000 000 đồng. Sau khi đã bán được 40 chiếc điện thoại với giá bằng \(120\% \)giá vốn mua ban đầu thì lượng khách hàng mua sản phẩm giảm xuống nên cửa hàng đã thực hiện chương trình giảm giá đặc biệt dành cho 10 chiếc điện thoại cuối cùng để thu hút khách hàng. Hỏi sau khi bán hết lô hàng trên, cửa hàng kỳ vọng lãi được 70 000 000 đồng thì phải giảm giá bao nhiêu phần trăm cho 10 chiếc điện thoại cuối cùng so với giá bán 40 chiếc điện thoại trước đó.
Tính giá vốn của 50 chiếc điện thoại.
Tính số tiền bán được của 40 chiếc điện thoại.
Tính giá tiền của một chiếc điện thoại khi bán với giá bằng \(120\% \)giá vốn.
Tính số tiền còn thiếu để được lãi \(70000000\) đồng từ lô hàng trên.
Tính giá tiền của một chiếc điện thoại sau khi giảm giá.
Tính phần trăm giá tiền của chiếc điện thoại sau khi giá so với giá bán trước đó.
Giá vốn của 50 chiếc điện thoại là:
\(50.10\,000\,000 = 500\,000\,000\) (đồng)
Số tiền bán được của 40 chiếc điện thoại là:
\(40.10\,000\,000.120\% = 480\,000\,000\) (đồng)
Giá tiền của một chiếc điện thoại khi bán với giá bằng \(120\% \) giá vốn là:
\(10\,000\,000.120\% = 12\,000\,000\) (đồng)
Số tiền còn thiếu để được lãi \(70\,000\,000\) đồng từ lô hàng trên là:
\(500\,000\,000 + 70\,000\,000 - 480\,000\,000 = 90\,000\,000\) (đồng)
Giá tiền của một chiếc điện thoại sau khi giảm giá là:
\(90\,000\,000:10 = 9\,000\,000\) (đồng)
Phần trăm giá tiền của chiếc điện thoại sau khi giá so với giá bán trước đó là:
\(\frac{{9\,000\,000}}{{12\,000\,000}} = 0,75 = 75\% \)
Vậy để lãi được \(70\,000\,000\) đồng từ lô hàng trên thì cửa hàng đã giảm \(100\% - 75\% = 25\% \) so với giá bán trước đó.
Đề thi giữa kì 1 Toán 7 - Đề số 12 là một bài kiểm tra quan trọng giúp học sinh đánh giá mức độ nắm vững kiến thức đã học trong nửa học kỳ đầu tiên của môn Toán lớp 7. Đề thi thường bao gồm các chủ đề chính như số tự nhiên, số nguyên, phân số, tỉ lệ thức, và các bài toán đại số cơ bản.
Cấu trúc đề thi có thể khác nhau tùy theo từng trường và giáo viên, nhưng thường bao gồm các phần sau:
Dưới đây là một số dạng bài tập thường xuất hiện trong đề thi giữa kì 1 Toán 7 - Đề số 12:
Các bài tập về số tự nhiên và số nguyên thường tập trung vào các phép toán cơ bản như cộng, trừ, nhân, chia, tìm ước, bội, và các tính chất của số tự nhiên và số nguyên.
Ví dụ: Tính giá trị của biểu thức: 12 + (-5) x 2 - 8 : 4
Phần này thường bao gồm các bài tập về quy đồng mẫu số, rút gọn phân số, so sánh phân số, và thực hiện các phép toán trên phân số.
Ví dụ: Rút gọn phân số: 24/36
Các bài tập về tỉ lệ thức yêu cầu học sinh nhận biết, lập tỉ lệ thức, và giải các bài toán liên quan đến tỉ lệ thức.
Ví dụ: Lập tỉ lệ thức từ các số sau: 2, 4, 6, 8
Phần này thường bao gồm các bài toán về giải phương trình đơn giản, tìm x, và các bài toán ứng dụng thực tế.
Ví dụ: Giải phương trình: x + 5 = 12
Để đạt kết quả tốt trong đề thi giữa kì 1 Toán 7 - Đề số 12, học sinh cần:
Để chuẩn bị tốt nhất cho đề thi giữa kì 1 Toán 7 - Đề số 12, học sinh có thể tham khảo các tài liệu sau:
Hãy dành thời gian ôn tập kiến thức một cách nghiêm túc và có kế hoạch. Đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè nếu gặp khó khăn trong quá trình học tập. Chúc các em học sinh đạt kết quả tốt trong đề thi giữa kì 1 Toán 7 - Đề số 12!
| Chủ đề | Mức độ quan trọng |
|---|---|
| Số tự nhiên và Số nguyên | Cao |
| Phân số | Trung bình |
| Tỉ lệ thức | Trung bình |
| Bài toán Đại số cơ bản | Thấp |
| Nguồn: giaitoan.edu.vn | |