Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 2 Toán 7 - Đề số 2 - Chân trời sáng tạo, một công cụ hữu ích giúp học sinh ôn luyện và đánh giá năng lực bản thân trước kỳ thi quan trọng. Đề thi được biên soạn theo chương trình học Toán 7, tập trung vào các kiến thức trọng tâm và có đáp án chi tiết đi kèm.
Đề thi này không chỉ giúp các em làm quen với cấu trúc đề thi mà còn rèn luyện kỹ năng giải quyết vấn đề, tư duy logic và áp dụng kiến thức vào thực tế.
I. TRẮC NGHIỆM ( 3 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
I. TRẮC NGHIỆM ( 3 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1. Thay tỉ số 1,25 : 3,45 bằng tỉ số giữa các số nguyên ta được
A. 12,5 : 34,5;
B. 29 : 65;
C. 25 : 69;
D. 1 : 3.
Câu 2. Biết 7x = 4y và y – x = 24. Khi đó, giá trị của x, y là
A. x = −56, y = −32;
B. x = 32, y = 56;
C. x = 56, y = 32;
D. x = 56, y = −32.
Câu 3. Biết y tỉ lệ thuận với x theo hệ số tỉ lệ k = 2. Khi x = –3 thì giá trị của y bằng bao nhiêu?
A. –6;
B. 0;
C. –9;
D. –1.
Câu 4. Cho x và y là hai đại lượng tỉ lệ nghịch với nhau và khi x = –12 thì y = 8. Khi x = 3 thì y bằng:
A. –32;
B. 32;
C. –2;
D. 2.
Câu 5. Biểu thức đại số biểu thị “Lập phương của tổng của hai số x và y” là
A. x3 – y3;
B. x + y;
C. x3 + y3;
D. (x + y)3.
Câu 6. Một tam giác có ba góc có số đo tỉ lệ với 3,4,5. Số đo ba góc của tam giác lần lượt là:
A. 450; 600; 750;
B. 300; 600; 900;
C. 200; 600; 1000;
D. Một kết quả khác.
Câu 7. Cho tam giác \(MNP\) có \(MN = MP\). Gọi \(A\) là trung điểm của \(NP\). Nếu \(\angle NMP = {50^0}\) thì số đo của \(\angle MPN\) là:
A. \({100^0}\).
B. \({130^0}\).
C. \({50^0}\).
D. \({65^0}\).
Câu 8. Cho tam giác \(ABC\) vuông tại \(A\) \(\left( {AB > AC} \right)\). Tia phân giác của góc \(B\) cắt \(AC\) ở \(D\). Kẻ \(DH\) vuông góc với \(BC\).Chọn câu đúng.
A. \(BH = BD\).
B. \(BH > BA\).
C. \(BH < BA\).
D. \(BH = BA\).
Câu 9. Cho tam giác MNP có: \(\widehat N = 70^\circ ;\widehat P = 55^\circ \). Khẳng định nào sau đây là đúng ?
A. MP < MN;
B. MP = MN;
C. MP > MN;
D. Không đủ dữ kiện so sánh.
Câu 10. Cho tam giác MNP có: MN < MP, MD ⊥ NP. Khẳng định nào sau đây là đúng?
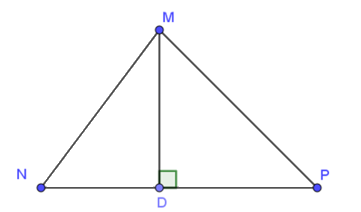
A. DN = DP;
B. MD < MP;
C. MD > MN;
D. MN = MP.
Câu 11. Bộ ba độ dài đoạn thẳng nào sau đây không thể tạo thành một tam giác?
A. 18cm; 28cm; 10cm;
B. 5cm; 4cm; 6cm;
C. 15cm; 18cm; 20cm;
D. 11cm; 9cm; 7cm.
Câu 12. Cho G là trọng tâm tam giác MNP có trung tuyến MK. Khẳng định nào sau đây là đúng?
A. \(\dfrac{{MG}}{{GK}} = \dfrac{1}{2}\);
B. \(\dfrac{{MG}}{{MK}} = \dfrac{1}{3}\) ;
C. \(\dfrac{{KG}}{{MK}} = \dfrac{1}{3}\);
D. \(\dfrac{{MG}}{{MK}} = \dfrac{2}{3}\).
II. PHẦN TỰ LUẬN (7,0 điểm)
Bài 1. (2 điểm) Tìm \(x\) biết:
a) \(x - \dfrac{2}{5} = \dfrac{{ - 9}}{{10}}\)
b) \(\dfrac{3}{4} + \dfrac{1}{4}x = \dfrac{{ - 5}}{6}\)
c) \(\dfrac{{x - 1}}{3} = \dfrac{{2 - x}}{{ - 2}}\)
Bài 2. (2 điểm) Tính chu vi của hình chữ nhật biết rằng chiều dài và chiều rộng của hình chữ nhật đó lần lượt tỉ lệ với \(5\,\,;\,\,3\) và hai lần chiều dài hơn ba lần chiều rộng là 8 cm.
Bài 3. (2,5 điểm) Cho \(\Delta ABC\) vuông tại \(A\), đường trung tuyến \(AM\). Trên tia đối của tia \(MA\) lấy điểm \(D\) sao cho \(DM = MA\).
a) Chứng minh \(\Delta AMB = \Delta DMC\).
b) Trên tia đối của tia \(CD\), lấy điểm \(I\) sao cho \(CI = CA\), qua điểm \(I\) vẽ đường thẳng song song với \(AC\) cắt \(AB\) tại \(E\). Chứng minh \(\Delta ACE = \Delta ICE\), từ đó suy ra \(\Delta ACE\) là tam giác vuông cân.
Bài 4. (0,5 điểm) Cho x,y,z thỏa mãn:\(\dfrac{x}{2} = \dfrac{y}{5} = \dfrac{z}{7}\) với x,y,z khác 0. Tính:
\(P = \dfrac{{x - y + z}}{{x + 2y - z}}\).
I. Trắc nghiệm
1.C | 2.B | 3. A | 4.A | 5.D | 6. A |
7.D | 8.D | 9.B | 10.B | 11.A | 12.C |
Câu 1.
Phương pháp
Nhân cả tử và mẫu của phân số với 1 số khác 0, ta được phân số có giá trị không đổi.
Lời giải
1,25 : 3,45 = 125 : 345 = 25 : 69.
Chọn C.
Câu 2.
Phương pháp
Áp dụng tính chất dãy tỉ số bằng nhau
Lời giải
Vì 7x = 4y nên \(\dfrac{x}{4} = \dfrac{y}{7}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{4} = \dfrac{y}{7} = \dfrac{{y - x}}{{7 - 4}} = \dfrac{{24}}{3} = 8\)
Do đó x = 4 . 8 = 32; y = 7 . 8 = 56.
Chọn B.
Câu 3.
Phương pháp
Đại lượng \(y\) tỉ lệ thuận với \(x\) theo hệ số tỉ lệ \(k\) thì \(y = kx\)
Lời giải
Khi x = - 3 thì \(y = kx = 2.( - 3) = - 6\)
Chọn A.
Câu 4.
Phương pháp
Tính chất hai đại lượng tỉ lệ nghịch: tích 2 giá trị tương ứng của 2 đại lượng luôn không đổi (bằng hệ số tỉ lệ)
Cách giải:
Hệ số tỉ lệ là: -12 . 8 = -96.
Khi x = 3 thì y = -96 : 3 = -32.
Chọn A
Câu 5.
Phương pháp
Mô tả
Cách giải:
Biểu thức đại số biểu thị “Lập phương của tổng của hai số x và y” là (x + y)3
Chọn D
Câu 6.
Phương pháp
Áp dụng:
Định lí Tổng định lí 3 góc trong một tam giác bằng 180 độ.
Tính chất của dãy tỉ số bằng nhau
Cách giải:
Gọi số đo 3 góc của tam giác lần lượt là a,b,c.
Vì tổng 3 góc trong một tam giác là 180 độ nên \(a + b + c = 180^\circ \).
Do số đo ba góc tỉ lệ với 3;4;5 nên \(\dfrac{a}{3} = \dfrac{b}{4} = \dfrac{c}{5}\).
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\begin{array}{l}\dfrac{a}{3} = \dfrac{b}{4} = \dfrac{c}{5} = \dfrac{{a + b + c}}{{3 + 4 + 5}} = \dfrac{{180}}{{12}} = 15\\ \Rightarrow a = 15.3 = 45;\\b = 15.4 = 60;\\c = 15.5 = 75.\end{array}\)
Chọn A.
Câu 7.
Phương pháp:
Vận dụng định lí:
+ Nếu ba cạnh của tam giác bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
+ Tổng ba góc trong một tam giác bằng \({180^0}\).
Cách giải:
* Vì \(A\) là trung điểm của \(NP\) nên \(AN = AP\) (tính chất trung điểm của đoạn thẳng)
* Xét \(\Delta AMN\) và \(\Delta AMP\) có:
\(MN = MP\) (giả thiết)
\(AN = AP\) (chứng minh trên)
\(AM\) là cạnh chung
Suy ra \(\Delta AMN = \Delta AMP\,\left( {c.c.c} \right)\)
Do đó, \(\angle MNA = \angle MPA\) (hai góc tương ứng) hay \(\angle MNP = \angle MPN\)
Xét \(\Delta MNP\) có: \(\angle MNP + NPM + \angle NMP = {180^0}\) (tổng ba góc trong một tam giác)
\(\begin{array}{l} \Rightarrow \angle MPN + \angle MPN + {50^0} = {180^0}\\ \Rightarrow 2\angle MPN = {180^0} - {50^0}\\ \Rightarrow 2\angle MPN = {130^0}\\ \Rightarrow \angle MPN = {130^0}:2\\ \Rightarrow \angle MPN = {65^0}\end{array}\)
Vậy \(\angle MPN = {65^0}\)
Chọn D.
Câu 8.
Phương pháp:
Chứng minh hai tam giác vuông bằng nhau theo trường hợp cạnh huyền – góc nhọn, từ đó suy ra cặp cạnh tương ứng bằng nhau.
Cách giải:
Xét \(\Delta BAD\) và \(\Delta BHD\) có:
\(\angle BAD = \angle BHD = 90^\circ \)
\(BD\) chung
\(\angle ABD = \angle HBD\) (vì \(BD\) là tia phân giác \(\angle B\))
\( \Rightarrow \Delta ABD = \Delta HBD\) (cạnh huyền – góc nhọn)
\( \Rightarrow BA = BH\)(hai cạnh tương ứng).
Chọn D.
Câu 9.
Phương pháp: Áp dụng định lí tổng ba góc trong tam giác, tính góc M.
Dựa vào quan hệ giữa cạnh và góc đối diện trong tam giác.
Cách giải:
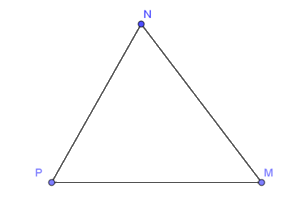
Xét tam giác MNP có: \(\widehat M + \widehat N + \widehat P = 180^\circ \) (định lí tổng ba góc trong một tam giác)
\( \Rightarrow \widehat M = 180^\circ - \widehat N - \widehat P = 180^\circ - 70^\circ - 55^\circ = 55^\circ \)
Ta được: \(\widehat M = \widehat P\)
Mà cạnh NP là cạnh đối của góc M, MN là cạnh đối của góc P.
Vậy NP = MN.
Chọn B.
Câu 10:
Phương pháp: Sử dụng mối quan hệ đường xiên và hình chiếu.
Sử dụng quan hệ đường vuông góc và đường xiên.
Cách giải:
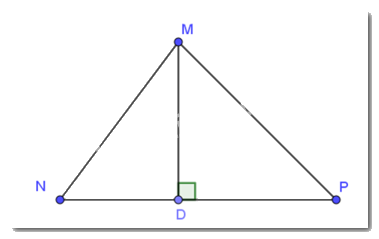
Trong tam giác MNP có MN < MP, hình chiếu của MN và MP trên cạnh NP lần lượt là ND và PD.
Do đó, ND < PD.
Ta có: MD < MP (đường vuông góc nhỏ hơn đường xiên)
Chọn B
Câu 11.
Phương pháp: Bất đẳng thức tam giác: Kiểm tra tổng độ dài 2 cạnh nhỏ hơn có lớn hơn độ dài cạnh lớn nhất không. Nếu không thì bộ 3 độ dài đó không tạo được thành tam giác.
Cách giải:
Vì 18 + 10 = 28 nên không thỏa mãn bất đẳng thức tam giác.
Do đó, bộ ba độ dài đoạn thẳng 18 cm; 28 cm; 10 cm không thể tạo thành một tam giác.
Chọn A.
Câu 12.
Phương pháp
Nếu \(\Delta ABC\) có trung tuyến \(AM\) và trọng tâm \(G\) thì \(AG = \dfrac{2}{3}AM\)
Lời giải
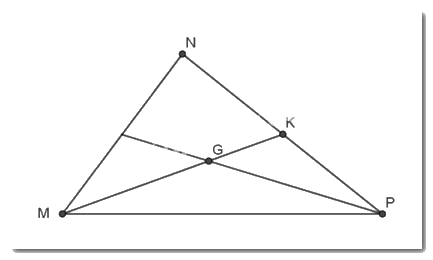
Vì G là trọng tâm tam giác MNP nên G là giao điểm của ba đường trung tuyến nên
\(MG = \dfrac{2}{3}MK;GK = \dfrac{1}{3}MK;MG = 2GK\)
Chọn C.
II. PHẦN TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm)
a) + b) Thực hiện các phép toán với số hữu tỉ.
c) Vận dụng định nghĩa hai phân thức bằng nhau.
Cách giải:
a) \(x - \dfrac{2}{5} = \dfrac{{ - 9}}{{10}}\)
\(\begin{array}{l}x = \dfrac{{ - 9}}{{10}} + \dfrac{2}{5}\\x = \dfrac{{ - 9 + 2.2}}{{10}}\\x = \dfrac{{ - 5}}{{10}} = \dfrac{{ - 1}}{2}\end{array}\)
Vậy \(x = - \dfrac{1}{2}\)
b) \(\dfrac{3}{4} + \dfrac{1}{4}x = \dfrac{{ - 5}}{6}\)
\(\begin{array}{l}\dfrac{1}{4}x = \dfrac{{ - 5}}{6} - \dfrac{3}{4}\\\dfrac{1}{4}x = \dfrac{{ - 5.2 - 3.3}}{{12}}\\\dfrac{1}{4}x = \dfrac{{ - 19}}{{12}}\\x = \dfrac{{ - 19}}{{12}}:\dfrac{1}{4}\\x = \dfrac{{ - 19}}{3}\end{array}\)
Vậy \(x = \dfrac{{ - 19}}{3}\)
c) \(\dfrac{{x - 1}}{3} = \dfrac{{2 - x}}{{ - 2}}\)
\(\begin{array}{l} - 2\left( {x - 1} \right) = 3\left( {2 - x} \right)\\ - 2x + 2 = 6 - 3x\\ - 2x + 3x = 6 - 2\\x = 4\end{array}\)
Vậy \(x = 4\)
Câu 2 (1 điểm)
Phương pháp:
Gọi chiều dài và chiều rộng của hình chữ nhật lần lượt là \(x,y\) (cm) (điều kiện: \(x,y > 0\))
Áp dụng tính chất của dãy tỉ số bằng nhau.
Cách giải:
Gọi chiều dài và chiều rộng của hình chữ nhật lần lượt là \(x,y\) (cm) (điều kiện: \(x,y > 0\))
Theo đề bài: chiều dài và chiều rộng của hình chữ nhật đó lần lượt tỉ lệ với \(5\,\,;\,\,3\) nên ta có: \(\dfrac{x}{5} = \dfrac{y}{3}\)
Hai lần chiều dài hơn ba lần chiều rộng là \(8\) cm nên \(2x - 3y = 8\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: \(\dfrac{x}{5} = \dfrac{y}{3} = \dfrac{{2x}}{{10}} = \dfrac{{3y}}{9} = \dfrac{{2x - 3y}}{{10 - 9}} = \dfrac{8}{1} = 8\)
Khi đó, \(\dfrac{x}{5} = 8 \Rightarrow x = 40\) (tmđk)
\(\dfrac{y}{3} = 8 \Rightarrow y = 24\) (tmđk)
Chu vi của hình chữ nhật là: \(2\left( {x + y} \right) = 2\left( {40 + 24} \right) = 128\) (cm)
Bài 5. (2,0 điểm)
Phương pháp:
a) Ta sẽ chứng minh: \(\Delta AMB = \Delta DMC\left( {c.g.c} \right)\)
b) Ta sẽ chứng minh: \(\angle EIC = {90^0}\), từ đó chứng minh được \(\Delta ACE = \Delta ICE\)(cạnh huyền – cạnh góc vuông)
\( \Rightarrow \angle ACE = \angle ICE\) (hai góc tương ứng)
\( \Rightarrow \Delta ACE\) vuông cân tại \(A\left( {\angle EAC = {{90}^0}} \right)\)
Cách giải:
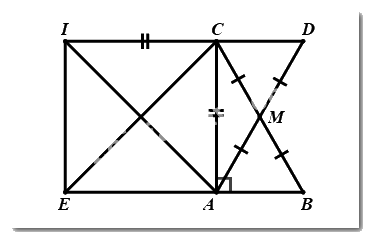
a) \(\Delta ABC\) vuông tại \(A,AM\) là đường trung tuyến\( \Rightarrow CM = BM\)
Ta có: \(\angle CMD = \angle AMB\) (hai góc đối đỉnh)
Xét \(\Delta AMB\) và \(\Delta DMC\) có:
\(\left. \begin{array}{l}CM = BM\left( {cmt} \right)\\\angle CMD = \angle AMB\left( {cmt} \right)\\AM = MD\left( {gt} \right)\end{array} \right\} \Rightarrow \Delta AMB = \Delta DMC\left( {c.g.c} \right)\)
b) Ta có: \(\Delta AMB = \Delta DMC\left( {cmt} \right) \Rightarrow \angle ABM = \angle DCM\) (hai góc tương ứng)
Mà hai góc \(\angle ABM;\angle DCM\) ở vị trí so le trong
\( \Rightarrow AB//CD\)
Mà \(AB \bot AC(\Delta ABC\) vuông tại \(A)\)
\( \Rightarrow CD \bot AC\) tại \(C \Rightarrow EI \bot CD\) tại \(I\) (vì \(EI//AC\)) hay \(\angle EIC = {90^0}\)
Xét \(\Delta ACE\) và \(\Delta ICE\) có:
\(\left. \begin{array}{l}\angle EAC = \angle EIC = {90^0}\\CE\,\,chung\\AC = IC\left( {gt} \right)\end{array} \right\} \Rightarrow \Delta ACE = \Delta ICE\) (cạnh huyền – cạnh góc vuông)
\( \Rightarrow \angle ACE = \angle ICE\) (hai góc tương ứng)
Mà \(\angle ICE = \angle AEC\) (vì \(AB//CD\))
\( \Rightarrow \angle ACE = \angle AEC\)
\( \Rightarrow \Delta ACE\) vuông cân tại \(A\left( {\angle EAC = {{90}^0}} \right)\)
Bài 4. (0,5 điểm)
Phương pháp:
Đặt \(\dfrac{x}{2} = \dfrac{y}{5} = \dfrac{z}{7} = k\)
Cách giải:
Đặt \(\dfrac{x}{2} = \dfrac{y}{5} = \dfrac{z}{7} = k \Rightarrow x = 2k;y = 5k;z = 7k.\)
Ta có: \(P = \dfrac{{x - y + z}}{{x + 2y - z}} = \dfrac{{2k - 5k + 7k}}{{2k + 2.5k - 7k}} = \dfrac{{4k}}{{5k}} = \dfrac{4}{5}.\)
Vậy \(P = \dfrac{4}{5}.\)
I. TRẮC NGHIỆM ( 3 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1. Thay tỉ số 1,25 : 3,45 bằng tỉ số giữa các số nguyên ta được
A. 12,5 : 34,5;
B. 29 : 65;
C. 25 : 69;
D. 1 : 3.
Câu 2. Biết 7x = 4y và y – x = 24. Khi đó, giá trị của x, y là
A. x = −56, y = −32;
B. x = 32, y = 56;
C. x = 56, y = 32;
D. x = 56, y = −32.
Câu 3. Biết y tỉ lệ thuận với x theo hệ số tỉ lệ k = 2. Khi x = –3 thì giá trị của y bằng bao nhiêu?
A. –6;
B. 0;
C. –9;
D. –1.
Câu 4. Cho x và y là hai đại lượng tỉ lệ nghịch với nhau và khi x = –12 thì y = 8. Khi x = 3 thì y bằng:
A. –32;
B. 32;
C. –2;
D. 2.
Câu 5. Biểu thức đại số biểu thị “Lập phương của tổng của hai số x và y” là
A. x3 – y3;
B. x + y;
C. x3 + y3;
D. (x + y)3.
Câu 6. Một tam giác có ba góc có số đo tỉ lệ với 3,4,5. Số đo ba góc của tam giác lần lượt là:
A. 450; 600; 750;
B. 300; 600; 900;
C. 200; 600; 1000;
D. Một kết quả khác.
Câu 7. Cho tam giác \(MNP\) có \(MN = MP\). Gọi \(A\) là trung điểm của \(NP\). Nếu \(\angle NMP = {50^0}\) thì số đo của \(\angle MPN\) là:
A. \({100^0}\).
B. \({130^0}\).
C. \({50^0}\).
D. \({65^0}\).
Câu 8. Cho tam giác \(ABC\) vuông tại \(A\) \(\left( {AB > AC} \right)\). Tia phân giác của góc \(B\) cắt \(AC\) ở \(D\). Kẻ \(DH\) vuông góc với \(BC\).Chọn câu đúng.
A. \(BH = BD\).
B. \(BH > BA\).
C. \(BH < BA\).
D. \(BH = BA\).
Câu 9. Cho tam giác MNP có: \(\widehat N = 70^\circ ;\widehat P = 55^\circ \). Khẳng định nào sau đây là đúng ?
A. MP < MN;
B. MP = MN;
C. MP > MN;
D. Không đủ dữ kiện so sánh.
Câu 10. Cho tam giác MNP có: MN < MP, MD ⊥ NP. Khẳng định nào sau đây là đúng?
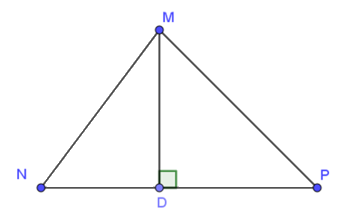
A. DN = DP;
B. MD < MP;
C. MD > MN;
D. MN = MP.
Câu 11. Bộ ba độ dài đoạn thẳng nào sau đây không thể tạo thành một tam giác?
A. 18cm; 28cm; 10cm;
B. 5cm; 4cm; 6cm;
C. 15cm; 18cm; 20cm;
D. 11cm; 9cm; 7cm.
Câu 12. Cho G là trọng tâm tam giác MNP có trung tuyến MK. Khẳng định nào sau đây là đúng?
A. \(\dfrac{{MG}}{{GK}} = \dfrac{1}{2}\);
B. \(\dfrac{{MG}}{{MK}} = \dfrac{1}{3}\) ;
C. \(\dfrac{{KG}}{{MK}} = \dfrac{1}{3}\);
D. \(\dfrac{{MG}}{{MK}} = \dfrac{2}{3}\).
II. PHẦN TỰ LUẬN (7,0 điểm)
Bài 1. (2 điểm) Tìm \(x\) biết:
a) \(x - \dfrac{2}{5} = \dfrac{{ - 9}}{{10}}\)
b) \(\dfrac{3}{4} + \dfrac{1}{4}x = \dfrac{{ - 5}}{6}\)
c) \(\dfrac{{x - 1}}{3} = \dfrac{{2 - x}}{{ - 2}}\)
Bài 2. (2 điểm) Tính chu vi của hình chữ nhật biết rằng chiều dài và chiều rộng của hình chữ nhật đó lần lượt tỉ lệ với \(5\,\,;\,\,3\) và hai lần chiều dài hơn ba lần chiều rộng là 8 cm.
Bài 3. (2,5 điểm) Cho \(\Delta ABC\) vuông tại \(A\), đường trung tuyến \(AM\). Trên tia đối của tia \(MA\) lấy điểm \(D\) sao cho \(DM = MA\).
a) Chứng minh \(\Delta AMB = \Delta DMC\).
b) Trên tia đối của tia \(CD\), lấy điểm \(I\) sao cho \(CI = CA\), qua điểm \(I\) vẽ đường thẳng song song với \(AC\) cắt \(AB\) tại \(E\). Chứng minh \(\Delta ACE = \Delta ICE\), từ đó suy ra \(\Delta ACE\) là tam giác vuông cân.
Bài 4. (0,5 điểm) Cho x,y,z thỏa mãn:\(\dfrac{x}{2} = \dfrac{y}{5} = \dfrac{z}{7}\) với x,y,z khác 0. Tính:
\(P = \dfrac{{x - y + z}}{{x + 2y - z}}\).
I. Trắc nghiệm
1.C | 2.B | 3. A | 4.A | 5.D | 6. A |
7.D | 8.D | 9.B | 10.B | 11.A | 12.C |
Câu 1.
Phương pháp
Nhân cả tử và mẫu của phân số với 1 số khác 0, ta được phân số có giá trị không đổi.
Lời giải
1,25 : 3,45 = 125 : 345 = 25 : 69.
Chọn C.
Câu 2.
Phương pháp
Áp dụng tính chất dãy tỉ số bằng nhau
Lời giải
Vì 7x = 4y nên \(\dfrac{x}{4} = \dfrac{y}{7}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{4} = \dfrac{y}{7} = \dfrac{{y - x}}{{7 - 4}} = \dfrac{{24}}{3} = 8\)
Do đó x = 4 . 8 = 32; y = 7 . 8 = 56.
Chọn B.
Câu 3.
Phương pháp
Đại lượng \(y\) tỉ lệ thuận với \(x\) theo hệ số tỉ lệ \(k\) thì \(y = kx\)
Lời giải
Khi x = - 3 thì \(y = kx = 2.( - 3) = - 6\)
Chọn A.
Câu 4.
Phương pháp
Tính chất hai đại lượng tỉ lệ nghịch: tích 2 giá trị tương ứng của 2 đại lượng luôn không đổi (bằng hệ số tỉ lệ)
Cách giải:
Hệ số tỉ lệ là: -12 . 8 = -96.
Khi x = 3 thì y = -96 : 3 = -32.
Chọn A
Câu 5.
Phương pháp
Mô tả
Cách giải:
Biểu thức đại số biểu thị “Lập phương của tổng của hai số x và y” là (x + y)3
Chọn D
Câu 6.
Phương pháp
Áp dụng:
Định lí Tổng định lí 3 góc trong một tam giác bằng 180 độ.
Tính chất của dãy tỉ số bằng nhau
Cách giải:
Gọi số đo 3 góc của tam giác lần lượt là a,b,c.
Vì tổng 3 góc trong một tam giác là 180 độ nên \(a + b + c = 180^\circ \).
Do số đo ba góc tỉ lệ với 3;4;5 nên \(\dfrac{a}{3} = \dfrac{b}{4} = \dfrac{c}{5}\).
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\begin{array}{l}\dfrac{a}{3} = \dfrac{b}{4} = \dfrac{c}{5} = \dfrac{{a + b + c}}{{3 + 4 + 5}} = \dfrac{{180}}{{12}} = 15\\ \Rightarrow a = 15.3 = 45;\\b = 15.4 = 60;\\c = 15.5 = 75.\end{array}\)
Chọn A.
Câu 7.
Phương pháp:
Vận dụng định lí:
+ Nếu ba cạnh của tam giác bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
+ Tổng ba góc trong một tam giác bằng \({180^0}\).
Cách giải:
* Vì \(A\) là trung điểm của \(NP\) nên \(AN = AP\) (tính chất trung điểm của đoạn thẳng)
* Xét \(\Delta AMN\) và \(\Delta AMP\) có:
\(MN = MP\) (giả thiết)
\(AN = AP\) (chứng minh trên)
\(AM\) là cạnh chung
Suy ra \(\Delta AMN = \Delta AMP\,\left( {c.c.c} \right)\)
Do đó, \(\angle MNA = \angle MPA\) (hai góc tương ứng) hay \(\angle MNP = \angle MPN\)
Xét \(\Delta MNP\) có: \(\angle MNP + NPM + \angle NMP = {180^0}\) (tổng ba góc trong một tam giác)
\(\begin{array}{l} \Rightarrow \angle MPN + \angle MPN + {50^0} = {180^0}\\ \Rightarrow 2\angle MPN = {180^0} - {50^0}\\ \Rightarrow 2\angle MPN = {130^0}\\ \Rightarrow \angle MPN = {130^0}:2\\ \Rightarrow \angle MPN = {65^0}\end{array}\)
Vậy \(\angle MPN = {65^0}\)
Chọn D.
Câu 8.
Phương pháp:
Chứng minh hai tam giác vuông bằng nhau theo trường hợp cạnh huyền – góc nhọn, từ đó suy ra cặp cạnh tương ứng bằng nhau.
Cách giải:
Xét \(\Delta BAD\) và \(\Delta BHD\) có:
\(\angle BAD = \angle BHD = 90^\circ \)
\(BD\) chung
\(\angle ABD = \angle HBD\) (vì \(BD\) là tia phân giác \(\angle B\))
\( \Rightarrow \Delta ABD = \Delta HBD\) (cạnh huyền – góc nhọn)
\( \Rightarrow BA = BH\)(hai cạnh tương ứng).
Chọn D.
Câu 9.
Phương pháp: Áp dụng định lí tổng ba góc trong tam giác, tính góc M.
Dựa vào quan hệ giữa cạnh và góc đối diện trong tam giác.
Cách giải:
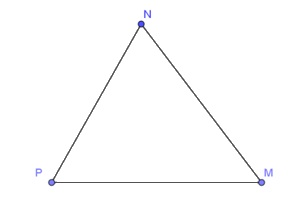
Xét tam giác MNP có: \(\widehat M + \widehat N + \widehat P = 180^\circ \) (định lí tổng ba góc trong một tam giác)
\( \Rightarrow \widehat M = 180^\circ - \widehat N - \widehat P = 180^\circ - 70^\circ - 55^\circ = 55^\circ \)
Ta được: \(\widehat M = \widehat P\)
Mà cạnh NP là cạnh đối của góc M, MN là cạnh đối của góc P.
Vậy NP = MN.
Chọn B.
Câu 10:
Phương pháp: Sử dụng mối quan hệ đường xiên và hình chiếu.
Sử dụng quan hệ đường vuông góc và đường xiên.
Cách giải:
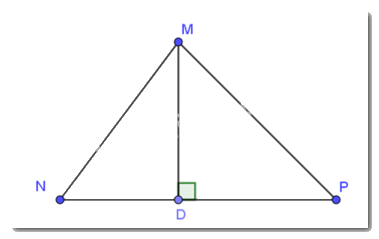
Trong tam giác MNP có MN < MP, hình chiếu của MN và MP trên cạnh NP lần lượt là ND và PD.
Do đó, ND < PD.
Ta có: MD < MP (đường vuông góc nhỏ hơn đường xiên)
Chọn B
Câu 11.
Phương pháp: Bất đẳng thức tam giác: Kiểm tra tổng độ dài 2 cạnh nhỏ hơn có lớn hơn độ dài cạnh lớn nhất không. Nếu không thì bộ 3 độ dài đó không tạo được thành tam giác.
Cách giải:
Vì 18 + 10 = 28 nên không thỏa mãn bất đẳng thức tam giác.
Do đó, bộ ba độ dài đoạn thẳng 18 cm; 28 cm; 10 cm không thể tạo thành một tam giác.
Chọn A.
Câu 12.
Phương pháp
Nếu \(\Delta ABC\) có trung tuyến \(AM\) và trọng tâm \(G\) thì \(AG = \dfrac{2}{3}AM\)
Lời giải
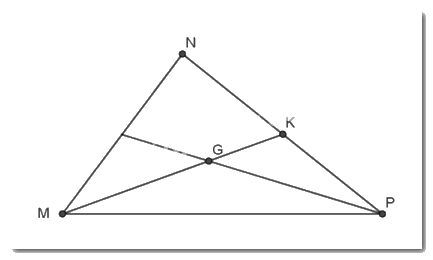
Vì G là trọng tâm tam giác MNP nên G là giao điểm của ba đường trung tuyến nên
\(MG = \dfrac{2}{3}MK;GK = \dfrac{1}{3}MK;MG = 2GK\)
Chọn C.
II. PHẦN TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm)
a) + b) Thực hiện các phép toán với số hữu tỉ.
c) Vận dụng định nghĩa hai phân thức bằng nhau.
Cách giải:
a) \(x - \dfrac{2}{5} = \dfrac{{ - 9}}{{10}}\)
\(\begin{array}{l}x = \dfrac{{ - 9}}{{10}} + \dfrac{2}{5}\\x = \dfrac{{ - 9 + 2.2}}{{10}}\\x = \dfrac{{ - 5}}{{10}} = \dfrac{{ - 1}}{2}\end{array}\)
Vậy \(x = - \dfrac{1}{2}\)
b) \(\dfrac{3}{4} + \dfrac{1}{4}x = \dfrac{{ - 5}}{6}\)
\(\begin{array}{l}\dfrac{1}{4}x = \dfrac{{ - 5}}{6} - \dfrac{3}{4}\\\dfrac{1}{4}x = \dfrac{{ - 5.2 - 3.3}}{{12}}\\\dfrac{1}{4}x = \dfrac{{ - 19}}{{12}}\\x = \dfrac{{ - 19}}{{12}}:\dfrac{1}{4}\\x = \dfrac{{ - 19}}{3}\end{array}\)
Vậy \(x = \dfrac{{ - 19}}{3}\)
c) \(\dfrac{{x - 1}}{3} = \dfrac{{2 - x}}{{ - 2}}\)
\(\begin{array}{l} - 2\left( {x - 1} \right) = 3\left( {2 - x} \right)\\ - 2x + 2 = 6 - 3x\\ - 2x + 3x = 6 - 2\\x = 4\end{array}\)
Vậy \(x = 4\)
Câu 2 (1 điểm)
Phương pháp:
Gọi chiều dài và chiều rộng của hình chữ nhật lần lượt là \(x,y\) (cm) (điều kiện: \(x,y > 0\))
Áp dụng tính chất của dãy tỉ số bằng nhau.
Cách giải:
Gọi chiều dài và chiều rộng của hình chữ nhật lần lượt là \(x,y\) (cm) (điều kiện: \(x,y > 0\))
Theo đề bài: chiều dài và chiều rộng của hình chữ nhật đó lần lượt tỉ lệ với \(5\,\,;\,\,3\) nên ta có: \(\dfrac{x}{5} = \dfrac{y}{3}\)
Hai lần chiều dài hơn ba lần chiều rộng là \(8\) cm nên \(2x - 3y = 8\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: \(\dfrac{x}{5} = \dfrac{y}{3} = \dfrac{{2x}}{{10}} = \dfrac{{3y}}{9} = \dfrac{{2x - 3y}}{{10 - 9}} = \dfrac{8}{1} = 8\)
Khi đó, \(\dfrac{x}{5} = 8 \Rightarrow x = 40\) (tmđk)
\(\dfrac{y}{3} = 8 \Rightarrow y = 24\) (tmđk)
Chu vi của hình chữ nhật là: \(2\left( {x + y} \right) = 2\left( {40 + 24} \right) = 128\) (cm)
Bài 5. (2,0 điểm)
Phương pháp:
a) Ta sẽ chứng minh: \(\Delta AMB = \Delta DMC\left( {c.g.c} \right)\)
b) Ta sẽ chứng minh: \(\angle EIC = {90^0}\), từ đó chứng minh được \(\Delta ACE = \Delta ICE\)(cạnh huyền – cạnh góc vuông)
\( \Rightarrow \angle ACE = \angle ICE\) (hai góc tương ứng)
\( \Rightarrow \Delta ACE\) vuông cân tại \(A\left( {\angle EAC = {{90}^0}} \right)\)
Cách giải:
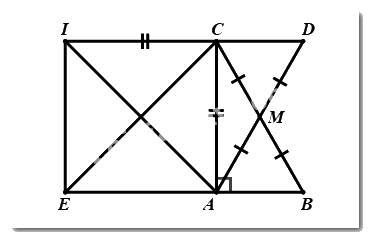
a) \(\Delta ABC\) vuông tại \(A,AM\) là đường trung tuyến\( \Rightarrow CM = BM\)
Ta có: \(\angle CMD = \angle AMB\) (hai góc đối đỉnh)
Xét \(\Delta AMB\) và \(\Delta DMC\) có:
\(\left. \begin{array}{l}CM = BM\left( {cmt} \right)\\\angle CMD = \angle AMB\left( {cmt} \right)\\AM = MD\left( {gt} \right)\end{array} \right\} \Rightarrow \Delta AMB = \Delta DMC\left( {c.g.c} \right)\)
b) Ta có: \(\Delta AMB = \Delta DMC\left( {cmt} \right) \Rightarrow \angle ABM = \angle DCM\) (hai góc tương ứng)
Mà hai góc \(\angle ABM;\angle DCM\) ở vị trí so le trong
\( \Rightarrow AB//CD\)
Mà \(AB \bot AC(\Delta ABC\) vuông tại \(A)\)
\( \Rightarrow CD \bot AC\) tại \(C \Rightarrow EI \bot CD\) tại \(I\) (vì \(EI//AC\)) hay \(\angle EIC = {90^0}\)
Xét \(\Delta ACE\) và \(\Delta ICE\) có:
\(\left. \begin{array}{l}\angle EAC = \angle EIC = {90^0}\\CE\,\,chung\\AC = IC\left( {gt} \right)\end{array} \right\} \Rightarrow \Delta ACE = \Delta ICE\) (cạnh huyền – cạnh góc vuông)
\( \Rightarrow \angle ACE = \angle ICE\) (hai góc tương ứng)
Mà \(\angle ICE = \angle AEC\) (vì \(AB//CD\))
\( \Rightarrow \angle ACE = \angle AEC\)
\( \Rightarrow \Delta ACE\) vuông cân tại \(A\left( {\angle EAC = {{90}^0}} \right)\)
Bài 4. (0,5 điểm)
Phương pháp:
Đặt \(\dfrac{x}{2} = \dfrac{y}{5} = \dfrac{z}{7} = k\)
Cách giải:
Đặt \(\dfrac{x}{2} = \dfrac{y}{5} = \dfrac{z}{7} = k \Rightarrow x = 2k;y = 5k;z = 7k.\)
Ta có: \(P = \dfrac{{x - y + z}}{{x + 2y - z}} = \dfrac{{2k - 5k + 7k}}{{2k + 2.5k - 7k}} = \dfrac{{4k}}{{5k}} = \dfrac{4}{5}.\)
Vậy \(P = \dfrac{4}{5}.\)
Kỳ thi giữa học kỳ 2 Toán 7 đóng vai trò quan trọng trong việc đánh giá quá trình học tập của học sinh. Đề thi giữa kì 2 Toán 7 - Đề số 2 - Chân trời sáng tạo là một bài kiểm tra được thiết kế để đánh giá mức độ nắm vững kiến thức và kỹ năng của học sinh sau khi học xong các chương trình Toán 7 trong học kỳ 1. Bài viết này sẽ cung cấp một cái nhìn tổng quan về đề thi, các dạng bài tập thường gặp, và hướng dẫn giải chi tiết để giúp học sinh tự tin hơn khi làm bài.
Đề thi thường bao gồm các phần sau:
Các chủ đề thường xuất hiện trong đề thi bao gồm:
Dưới đây là một số dạng bài tập thường gặp trong đề thi giữa kì 2 Toán 7 - Đề số 2 - Chân trời sáng tạo:
Ví dụ 1: Giải phương trình 2x + 5 = 11
Lời giải:
2x + 5 = 11
2x = 11 - 5
2x = 6
x = 6 / 2
x = 3
Ví dụ 2: Cho tam giác ABC, biết góc A = 60 độ, góc B = 80 độ. Tính góc C.
Lời giải:
Tổng ba góc trong một tam giác bằng 180 độ.
Góc C = 180 độ - góc A - góc B
Góc C = 180 độ - 60 độ - 80 độ
Góc C = 40 độ
Để đạt kết quả tốt trong kỳ thi giữa học kỳ 2 Toán 7, học sinh cần:
Giaitoan.edu.vn cung cấp nhiều tài nguyên hỗ trợ học tập, bao gồm:
Hy vọng rằng bài viết này sẽ giúp các em học sinh tự tin hơn khi làm bài thi giữa kì 2 Toán 7 - Đề số 2 - Chân trời sáng tạo. Chúc các em học tập tốt!