Chào mừng các em học sinh lớp 7 đến với đề thi học kì 2 môn Toán, đề số 12, chương trình Chân trời sáng tạo.
Đề thi này được thiết kế để giúp các em ôn tập và đánh giá kiến thức đã học trong học kì 2, chuẩn bị tốt nhất cho kỳ thi sắp tới.
Trong các phát biểu sau, phát biểu nào đúng?
Giá trị x thoả mãn tỉ lệ thức: \(\frac{6}{x} = \frac{{ - 10}}{5}\)
Trong các công thức sau, công thức nào phát biểu: “Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ 2”?
Biểu thức đại số biểu diễn công thức tính diện tích hình thang có 2 đáy độ dài a, b; chiều cao h ( a, b, h có cùng đơn vị đo độ dài)
Hệ số tự do của đa thức \( - {x^7} + 5{x^5} - 12x - 22\) là
Giá trị của đa thức \(g\left( x \right) = {x^8}{\rm{ + }}{x^4} + {x^2} + 1\) tại \(x = - 1\)bằng
Trong các biến cố sau, biến cố nào là biến cố ngẫu nhiên?
Gieo một đồng xu cân đối, đồng chất 1 lần. Xác suất của biến cố “Đồng xu xuất hiện mặt ngửa” là
Cho \(\Delta ABC\) vuông tại A có \(\widehat B = {65^0}.\) Chọn khẳng định đúng.
Cho tam giác \(ABC\) có AM là đường trung tuyến, trọng tâm \(G\). Khẳng định nào sau đây đúng?
Bộ ba số nào là độ dài ba cạnh của một tam giác?
Cho \(\Delta ABC\) có \(\widehat A = {35^0};\widehat B = {45^0}\). Số đo góc C là:
a) Tính giá trị của biểu thức \(A = (2x + y)(2x - y)\) tại \(x = - 2,\;y = \frac{1}{3}.\)
b) Tìm tất cả các giá trị của \(x\) thoả mãn \(x(3x - 2) - 3{x^2} = \frac{3}{4}.\)
Học sinh của ba lớp 7A, 7B, 7C làm 40 tấm thiệp để chúc mừng các thầy cô nhân ngày 20-11, biết số học sinh của ba lớp 7A, 7B, 7C theo thứ tự là 45; 42; 33. Hỏi trong ba lớp trên mỗi lớp làm bao nhiêu tấm thiệp, biết số học sinh tỉ lệ với số thiệp cần làm.
Cho hai đa thức \(A\left( x \right) = 5{x^4} - 7{x^2} - 3x - 6{x^2} + 11x - 30\) và \(B\left( x \right) = - 11{x^3} + 5x - 10 + 13{x^4} - 2 + 20{x^3} - 34x\)
a) Thu gọn hai đa thức \(A\left( x \right)\) và \(B\left( x \right)\) và sắp xếp theo lũy thừa giảm dần của biến.
b) Tính \(A\left( x \right) - B\left( x \right)\).
Cho tam giác ABC cân tại A. Kẻ \(BH \bot AC;CK \bot AB\) (\(H \in AC;\,\)\(K \in AB\)).
a) Chứng minh tam giác AKH là tam giác cân
b) Gọi I là giao của BH và CK; AI cắt BC tại M. Chứng minh rằng IM là phân giác của \(\widehat {BIC}\).
c) Chứng minh: \(HK\,{\rm{//}}\,BC\).
Tìm tất cả các số nguyên dương \(x,y,z\) thỏa mãn:
\(\frac{{2z - 4x}}{3} = \frac{{3x - 2y}}{4} = \frac{{4y - 3z}}{2}\)và \(200 < {y^2} + {z^2} < 450\).
Trong các phát biểu sau, phát biểu nào đúng?
Đáp án : B
Dựa vào kiến thức về tỉ lệ thức.
Ta có:
\(\frac{1}{2} = \frac{2}{4} \ne \frac{{ - 2}}{4}\) nên A sai.
\(\frac{1}{2} = \frac{5}{{10}}\) nên B đúng.
\(\frac{1}{2} = \frac{2}{4} \ne \frac{3}{4}\) nên C sai.
\(\frac{1}{2} = \frac{{ - 3}}{{ - 6}} \ne \frac{{ - 2}}{{ - 6}}\) nên D sai.
Đáp án B.
Giá trị x thoả mãn tỉ lệ thức: \(\frac{6}{x} = \frac{{ - 10}}{5}\)
Đáp án : B
Dựa vào kiến thức về tỉ lệ thức: Nếu \(\frac{a}{b} = \frac{c}{d}\) thì \(ad = bc\).
Ta có: \(\frac{6}{x} = \frac{{ - 10}}{5}\) nên
\(\begin{array}{l}6.5 = \left( { - 10} \right).x\\x = \frac{{6.5}}{{ - 10}}\\x = - 3\end{array}\)
Đáp án B.
Trong các công thức sau, công thức nào phát biểu: “Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ 2”?
Đáp án : A
Sử dụng kiến thức về hai đại lượng tỉ lệ thuận: Nếu đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ là a thì ta có công thức \(y = ax\)
Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ 2 nên y = 2x.
Đáp án A.
Biểu thức đại số biểu diễn công thức tính diện tích hình thang có 2 đáy độ dài a, b; chiều cao h ( a, b, h có cùng đơn vị đo độ dài)
Đáp án : D
Sử dụng công thức tính diện tích hình thang để viết biểu thức.
Biểu thức đại số biểu diễn công thức tính diện tích hình thang có 2 đáy độ dài a, b; chiều cao h ( a, b, h có cùng đơn vị đo độ dài) là: \(\frac{{\left( {a + b} \right).h}}{2}\).
Đáp án D.
Hệ số tự do của đa thức \( - {x^7} + 5{x^5} - 12x - 22\) là
Đáp án : A
Hệ số của hạng tử bậc 0 gọi là hệ số tự do của đa thức đó.
Hệ số tự do của đa thức \( - {x^7} + 5{x^5} - 12x - 22\) là – 22.
Đáp án A.
Giá trị của đa thức \(g\left( x \right) = {x^8}{\rm{ + }}{x^4} + {x^2} + 1\) tại \(x = - 1\)bằng
Đáp án : D
Thay \(x = - 1\) vào đa thức để tính giá trị.
Thay \(x = - 1\) vào đa thức g(x) ta được:
\(g\left( x \right) = {\left( { - 1} \right)^8}{\rm{ + }}{\left( { - 1} \right)^4} + {\left( { - 1} \right)^2} + 1 = 1 + 1 + 1 + 1 = 4\)
Đáp án D.
Trong các biến cố sau, biến cố nào là biến cố ngẫu nhiên?
Đáp án : D
Dựa vào kiến thức về các loại biến cố.
Biến cố “Gieo hai con xúc xắc 1 lần, tổng số chấm xuất hiện trên hai con xúc xắc là 7” là biến cố ngẫu nhiên.
Đáp án D.
Gieo một đồng xu cân đối, đồng chất 1 lần. Xác suất của biến cố “Đồng xu xuất hiện mặt ngửa” là
Đáp án : C
Dựa vào kiến thức về xác suất của các biến cố đồng khả năng.
Do đồng xu cân đối nên biến cố “Đồng xu xuất hiện mặt ngửa” và “Đồng xu xuất hiện mặt sấp” là đồng khả năng nên xác suất của 2 biến cố này bằng nhau và bằng \(\frac{1}{2}\).
Đáp án C.
Cho \(\Delta ABC\) vuông tại A có \(\widehat B = {65^0}.\) Chọn khẳng định đúng.
Đáp án : B
Dựa vào mối quan hệ giữa góc và cạnh đối nhau trong một tam giác và định lí tổng ba góc của một tam giác bằng \({180^0}\).
Tam giác ABC vuông tại A có \(\widehat B = {65^0}\) nên
\(\widehat C = {180^0} - \widehat A - \widehat B = {180^0} - {90^0} - {65^0} = {25^0}\).
Vì \(\widehat A > \widehat B > \widehat C\left( {{{90}^0} > {{65}^0} > {{25}^0}} \right)\) nên \(BC > AC > AB\).
Đáp án B.
Cho tam giác \(ABC\) có AM là đường trung tuyến, trọng tâm \(G\). Khẳng định nào sau đây đúng?
Đáp án : B
Dựa vào kiến thức về trọng tâm của tam giác.
Vì G là trọng tâm của tam giác ABC nên \(AG = \frac{2}{3}AM\) suy ra \(GM = AM - AG = AM - \frac{2}{3}AM = \frac{1}{3}AM\).
Suy ra \(\frac{{GM}}{{AG}} = \frac{{\frac{1}{3}AM}}{{\frac{2}{3}AM}} = \frac{1}{2}\) hay \(AG = 2GM\).
Đáp án B.
Bộ ba số nào là độ dài ba cạnh của một tam giác?
Đáp án : C
Dựa vào quan hệ giữa các cạnh của một tam giác.
Ta có:
4 + 5 = 9 < 10, ba độ dài \(4cm,\;5cm,\;10cm\) không thỏa mãn một bất đẳng thức tam giác nên không là độ dài ba cạnh của một tam giác.
5 + 5 = 10 < 12, ba độ dài \(5cm,\;5cm,\;12cm\) không thỏa mãn một bất đẳng thức tam giác nên không là độ dài ba cạnh của một tam giác.
11 > 20 – 11 = 9, ba độ dài \(11cm,\;11cm,\;20cm\) thỏa mãn điều kiện của bất đẳng thức tam giác nên đây có thể là độ dài ba cạnh của một tam giác.
11 = 20 – 9, ba độ dài \(9cm,\;20cm,\;11cm\) không thỏa mãn một bất đẳng thức tam giác nên không là độ dài ba cạnh của một tam giác.
Đáp án C.
Cho \(\Delta ABC\) có \(\widehat A = {35^0};\widehat B = {45^0}\). Số đo góc C là:
Đáp án : D
Dựa vào định lí tổng ba góc của một tam giác bằng \({180^0}\).
Số đo góc C là:
\(\begin{array}{l}\widehat C = {180^0} - \widehat A - \widehat B\\ = {180^0} - {35^0} - {45^0}\\ = {100^0}\end{array}\)
Đáp án D.
a) Tính giá trị của biểu thức \(A = (2x + y)(2x - y)\) tại \(x = - 2,\;y = \frac{1}{3}.\)
b) Tìm tất cả các giá trị của \(x\) thoả mãn \(x(3x - 2) - 3{x^2} = \frac{3}{4}.\)
a) Thay \(x = - 2,\;y = \frac{1}{3}\) vào A để tính giá trị biểu thức.
b) Sử dụng các phép tính với đa thức một biến để tìm giá trị của x.
a) Tại \(x = - 2,\;y = \frac{1}{3}\) ta có
\(\begin{array}{l}A = \left[ {2 \cdot ( - 2) + \frac{1}{3}} \right]\left[ {2 \cdot ( - 2) - \frac{1}{3}} \right]\\ = \left( { - 4 + \frac{1}{3}} \right)\left( { - 4 - \frac{1}{3}} \right)\\ = \frac{{ - 11}}{3}.\frac{{ - 13}}{3}\\ = \frac{{143}}{9}.\end{array}\)
b) \(x(3x - 2) - 3{x^2} = \frac{3}{4}\)
\(\begin{array}{l}3{x^2} - 2x - 3{x^2} = \frac{3}{4}\\ - 2x = \frac{3}{4}\\x = \frac{{ - 3}}{8}.\end{array}\)
Vậy \(x = \frac{{ - 3}}{8}\).
Học sinh của ba lớp 7A, 7B, 7C làm 40 tấm thiệp để chúc mừng các thầy cô nhân ngày 20-11, biết số học sinh của ba lớp 7A, 7B, 7C theo thứ tự là 45; 42; 33. Hỏi trong ba lớp trên mỗi lớp làm bao nhiêu tấm thiệp, biết số học sinh tỉ lệ với số thiệp cần làm.
Gọi số tấm thiệp của ba lớp 7A, 7B, 7C lần lượt là \(x,y,z\left( {x,y,z \in {\mathbb{N}^ * }} \right)\)
Viết phương trình dựa vào đề bài.
Áp dụng tính chất dãy tỉ số bằng nhau để tìm x, y, z.
Gọi số tấm thiệp của ba lớp 7A, 7B, 7C lần lượt là \(x,y,z\left( {x,y,z \in {\mathbb{N}^ * }} \right)\)
Vì có 40 tấm thiệp nên x + y + z = 40
Vì số học sinh tỉ lệ với số thiệp cần làm nên ta có \(\frac{x}{{45}} = \frac{y}{{42}} = \frac{z}{{33}}\).
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{{45}} = \frac{y}{{42}} = \frac{z}{{33}} = \frac{{x + y + z}}{{45 + 42 + 33}} = \frac{{40}}{{120}} = \frac{1}{3}\)
suy ra \( x = \frac{1}{3}.45 = 15; y = \frac{1}{3}.42 = 14; z = \frac{1}{3}.33 = 11\)
Vậy số tấm thiệp của ba lớp 7A, 7B, 7C lần lượt là 15; 14; 11.
Cho hai đa thức \(A\left( x \right) = 5{x^4} - 7{x^2} - 3x - 6{x^2} + 11x - 30\) và \(B\left( x \right) = - 11{x^3} + 5x - 10 + 13{x^4} - 2 + 20{x^3} - 34x\)
a) Thu gọn hai đa thức \(A\left( x \right)\) và \(B\left( x \right)\) và sắp xếp theo lũy thừa giảm dần của biến.
b) Tính \(A\left( x \right) - B\left( x \right)\).
Thực hiện tính toán với đa thức một biến.
a) \(A\left( x \right) = 5{x^4} - 7{x^2} - 3x - 6{x^2} + 11x - 30\)
\(\begin{array}{l} = 5{x^4} + \left( { - 7{x^2} - 6{x^2}} \right) + \left( { - 3x + 11x} \right) - 30\\ = 5{x^4} - 13{x^2} + 8x - 30\end{array}\)
\(B\left( x \right) = - 11{x^3} + 5x - 10 + 13{x^4} - 2 + 20{x^3} - 34x\)
\(\begin{array}{l} = 13{x^4} + \left( { - 11{x^3} + 20{x^3}} \right) + \left( {5x - 34x} \right) + \left( { - 10 - 2} \right)\\ = 13{x^4} + 9{x^3} - 29x - 12\end{array}\)
b) \(A\left( x \right) - B\left( x \right) = \left( {5{x^4} - 13{x^2} + 8x - 30} \right) - \left( {13{x^4} + 9{x^3} - 29x - 12} \right)\)
\(\begin{array}{l} = 5{x^4} - 13{x^2} + 8x - 30 - 13{x^4} - 9{x^3} + 29x + 12\\ = \left( {5{x^4} - 13{x^4}} \right) - 9{x^3} - 13{x^2} + \left( {8x + 29x} \right) + \left( { - 30 + 12} \right)\\ = -8{x^4} - 9{x^3} - 13{x^2} + 37x - 18\end{array}\)
Cho tam giác ABC cân tại A. Kẻ \(BH \bot AC;CK \bot AB\) (\(H \in AC;\,\)\(K \in AB\)).
a) Chứng minh tam giác AKH là tam giác cân
b) Gọi I là giao của BH và CK; AI cắt BC tại M. Chứng minh rằng IM là phân giác của \(\widehat {BIC}\).
c) Chứng minh: \(HK\,{\rm{//}}\,BC\).
a) Chứng minh \(\Delta ABH = \Delta ACK\) theo trường hợp cạnh huyền – góc nhọn. suy ra AH = AK nên tam giác AKH là tam giác cân.
b) Chứng minh \(\widehat {{P_1}} = \widehat {{N_1}}\) nên \(\Delta AKI = \Delta AHI\) theo trường hợp cạnh huyền – cạnh góc vuông suy ra \(\widehat {AIK} = \widehat {AIH}\)
Từ đó ta có \(\widehat {CIM} = \widehat {BIM}\) nên IM là phân giác của góc BIC
c) Từ tam giác cân ABC và AHK ta có \(\widehat {ABC} = \frac{{180^\circ - \widehat A}}{2}\), \(\widehat {AKH} = \frac{{180^\circ - \widehat A}}{2}\) nên \(\widehat {ABC} = \widehat {AKH}\).
Mà hai góc này ở vị trí đồng vị nên HK // BC.
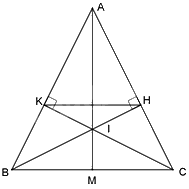
a) Xét \(\Delta ABH\) và \(\Delta ACK\) có:
\(\widehat {AHB} = \widehat {AKC} = 90^\circ \) (vì \(BH \bot AC;CK \bot AB\))
AB = AC (\(\Delta ABC\) cân);
góc A chung;
Do đó: \(\Delta ABH = \Delta ACK\) (cạnh huyền – góc nhọn).
\( \Rightarrow AH = AK \Rightarrow \Delta AHK\) cân tại A (đpcm).
b) Xét \(\Delta AKI\) và \(\Delta AHI\) có: \(\widehat {AKI} = \widehat {AHI} = 90^\circ \) (vì \(BH \bot AC;CK \bot AB\))
AK = AH (\(\Delta AHK\) cân tại A);
cạnh AI chung;
Do đó: \(\Delta AKI = \Delta AHI\) (cạnh huyền – cạnh góc vuông).
\( \Rightarrow \widehat {AIK} = \widehat {AIH}\).
Mà: \(\widehat {AIK} = \widehat {CIM};\widehat {AIH} = \widehat {BIM}\) (2 góc đối đỉnh).
Do đó: \(\widehat {CIM} = \widehat {BIM}\)\( \Rightarrow IM\)là phân giác của góc BIC (đpcm).
c) \(\Delta ABC\) cân tại A nên: \(\widehat {ABC} = \frac{{180^\circ - \widehat A}}{2}\) .
\(\Delta AHK\) cân tại A nên: \(\widehat {AKH} = \frac{{180^\circ - \widehat A}}{2}\) .
Suy ra \(\widehat {ABC} = \widehat {AKH}\).
Mà 2 góc này ở vị trí đồng vị.
Do đó: KH // BC (đpcm).
Tìm tất cả các số nguyên dương \(x,y,z\) thỏa mãn:
\(\frac{{2z - 4x}}{3} = \frac{{3x - 2y}}{4} = \frac{{4y - 3z}}{2}\)và \(200 < {y^2} + {z^2} < 450\).
Biến đổi \(\frac{{2z - 4x}}{3} = \frac{{3x - 2y}}{4} = \frac{{4y - 3z}}{2}\) thành \(\frac{{6z - 12x}}{9} = \frac{{12x - 8y}}{{16}} = \frac{{8y - 6z}}{4}\).
Áp dụng tính chất dãy tỉ số bằng nhau để suy ra \(\frac{{2z - 4x}}{3} = \frac{{3x - 2y}}{4} = \frac{{4y - 3z}}{2} = 0\)
Từ đó ta có \(6z = 12x = 8y\).
Đặt \(6z = 12x = 8y = 24k\left( {k > 0} \right) \Rightarrow \left( {x;y;z} \right) = \left( {2k;3k;4k} \right)\)
Tìm k dựa vào \(200 < {y^2} + {z^2} < 450\)
Từ đó tính được x, y, z.
Ta có \(\frac{{2z - 4x}}{3} = \frac{{3x - 2y}}{4} = \frac{{4y - 3z}}{2}\) nên
\(\begin{array}{l}\frac{{3\left( {z - 4x} \right)}}{{3.3}} = \frac{{4\left( {3x - 2y} \right)}}{{4.4}} = \frac{{2\left( {4y - 3z} \right)}}{{2.2}}\\\frac{{6z - 12x}}{9} = \frac{{12x - 8y}}{{16}} = \frac{{8y - 6z}}{4}\end{array}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{{6z - 12x}}{9} = \frac{{12x - 8y}}{{16}} = \frac{{8y - 6z}}{4} = \frac{{6z - 12x + 12x - 8y + 8y - 6z}}{{9 + 16 + 4}} = \frac{0}{{29}} = 0\)
Do đó \(\left\{ \begin{array}{l}6z - 12x = 0\\12x - 8y = 0\\8y - 6z = 0\end{array} \right.\) hay \(6z = 12x = 8y\).
Đặt \(6z = 12x = 8y = 24k\left( {k > 0} \right)\) ta được \(\left( {x;y;z} \right) = \left( {2k;3k;4k} \right)\)
Theo giả thiết \(200 < {y^2} + {z^2} < 450\)
nên \(200 < (3k)^2 + (4k)^2 < 450\)
\(200 < 9{k^2} + 16{k^2} < 450\)
suy ra \(200 < 25{k^2} < 450\)
\(8 < k^2 < 18\)
Do đó \(k \in \left\{ {3;4} \right\}\)
Từ đó tìm được \(\left( {x;y;z} \right) \in \left\{ {\left( {6;9;12} \right);\left( {8;12;16} \right)} \right\}\)
Kỳ thi học kì 2 Toán 7 đóng vai trò quan trọng trong việc đánh giá năng lực học tập của học sinh sau một học kỳ rèn luyện kiến thức. Đề thi học kì 2 Toán 7 - Đề số 12 - Chân trời sáng tạo là một trong những đề thi được nhiều trường học lựa chọn để đánh giá học sinh. Bài viết này sẽ cung cấp thông tin chi tiết về cấu trúc đề thi, các dạng bài tập thường gặp, và hướng dẫn giải chi tiết để giúp các em học sinh ôn tập hiệu quả.
Đề thi học kì 2 Toán 7 - Đề số 12 - Chân trời sáng tạo thường bao gồm các phần sau:
Các chủ đề thường xuất hiện trong đề thi bao gồm:
Dưới đây là một số dạng bài tập thường gặp trong Đề thi học kì 2 Toán 7 - Đề số 12 - Chân trời sáng tạo:
Các bài tập này yêu cầu học sinh thực hiện các phép tính cộng, trừ, nhân, chia với số hữu tỉ và số thực. Ví dụ:
Tính: (1/2) + (3/4) - (5/8)
Học sinh cần giải các phương trình và bất phương trình bậc nhất một ẩn. Ví dụ:
Giải phương trình: 2x + 5 = 11
Các bài tập này yêu cầu học sinh xác định hàm số tuyến tính, vẽ đồ thị hàm số, và giải các bài toán liên quan đến hàm số. Ví dụ:
Cho hàm số y = 2x - 1. Tìm giá trị của y khi x = 3.
Các bài tập hình học yêu cầu học sinh chứng minh các tính chất hình học, tính góc, tính độ dài đoạn thẳng, và giải các bài toán liên quan đến tam giác, tứ giác. Ví dụ:
Cho tam giác ABC vuông tại A. Tính độ dài cạnh BC biết AB = 3cm và AC = 4cm.
Để giải tốt các bài tập trong Đề thi học kì 2 Toán 7 - Đề số 12 - Chân trời sáng tạo, học sinh cần nắm vững kiến thức cơ bản, hiểu rõ các định nghĩa, định lý, và công thức toán học. Ngoài ra, học sinh cần luyện tập thường xuyên để rèn luyện kỹ năng giải toán.
Dưới đây là một số lời khuyên hữu ích:
Để chuẩn bị tốt nhất cho kỳ thi học kì 2 Toán 7, học sinh có thể tham khảo các tài liệu sau:
Đề thi học kì 2 Toán 7 - Đề số 12 - Chân trời sáng tạo là một cơ hội để học sinh đánh giá năng lực học tập của mình và chuẩn bị tốt nhất cho các kỳ thi tiếp theo. Hy vọng rằng với những thông tin và hướng dẫn chi tiết trong bài viết này, các em học sinh sẽ tự tin và đạt kết quả tốt nhất trong kỳ thi sắp tới.