Giaitoan.edu.vn xin giới thiệu Đề thi học kì 1 Toán 7 Chân trời sáng tạo - Đề số 11, một công cụ hữu ích giúp học sinh ôn luyện và đánh giá năng lực bản thân trước kỳ thi quan trọng.
Đề thi được biên soạn bám sát chương trình học, bao gồm các dạng bài tập khác nhau, từ cơ bản đến nâng cao, giúp học sinh làm quen với cấu trúc đề thi thực tế.
Cùng với đề thi, chúng tôi cung cấp đáp án chi tiết và lời giải bài tập, giúp học sinh tự học hiệu quả và nắm vững kiến thức.
Khẳng định nào sau đây sai:
Số đối của \(\frac{5}{6}\) là:
Căn bậc hai số học của 196 là:
Số nào là số vô tỉ trong các số sau:
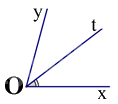
Cho \(\widehat {{\rm{xOy}}} = {70^0}\)và tia Ot là tia phân giác của \(\widehat {{\rm{xOy}}}\). Số đo \(\widehat {{\rm{xOt}}}\) bằng:
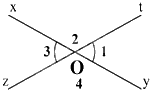
Cho hình vẽ bên, biết \({\widehat {\rm{O}}_1} = {60^0}\). Số đo \({\widehat {\rm{O}}_3}\) là:
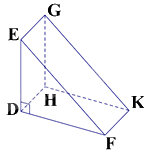
Quan sát hình lăng trụ. ở hình bên. Hãy chọn câu đúng:
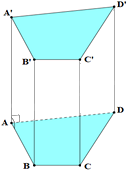
Hãy chọn câu sai. Hình lăng trụ đứng tứ giác có:
Trong các dữ liệu sau, dữ liệu nào không phải là dữ liệu định lượng?
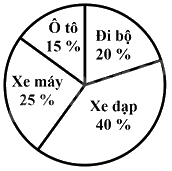
Theo số liệu biểu đồ hình quạt tròn ở hình bên thì tỉ lệ phần trăm đi xe đạp đến trường của các em học sinh ở một trường THCS là:
Kết quả tìm hiểu về sở thích chơi game của một số học sinh trong một trường
THCS được ghi bởi bảng thống kê sau. Hãy cho biết nhiều học sinh lựa chọn loại nào nhất?

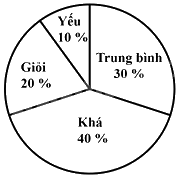
Biểu đồ hình quạt tròn ở hình bên biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) xếp loại học lực giữa kì I của học sinh lớp 7A. Hỏi học sinh đạt loại gì là nhiều nhất?
Thực hiện phép tính:
a) \({\left( {\frac{2}{3} - 1} \right)^2} - \frac{3}{5}:\frac{9}{{10}} + {1^{2022}}\).
b) \(\frac{8}{7} \cdot \left| {\frac{{ - 3}}{5}} \right| + \frac{8}{7} \cdot \sqrt {\frac{4}{{25}}} - \frac{{\sqrt 9 }}{4}\).
Tìm x, biết:
a) \(x + 0,75 = \frac{2}{3}\).
b) \(\left| {\frac{1}{2} - x} \right| = \frac{4}{5}\).
Diện tích nước Việt Nam là 331 698 km2. Hãy làm tròn diện tích này đến hàng nghìn.
Một tủ gỗ có dạng hình hộp chữ nhật có kích thước: dài 70cm, rộng 60cm, cao 200cm như hình bên. Người ta muốn sơn tất cả các mặt của cây tủ trừ mặt tiếp giáp với mặt đất thì không sơn.

a) Tính diện tích xung quanh của cây tủ và tính diện tích phần cần sơn?
b) Chi phí để sơn mỗi m2 tủ là 100 000 đồng. Hỏi tổng chi phí để sơn là bao nhiêu?
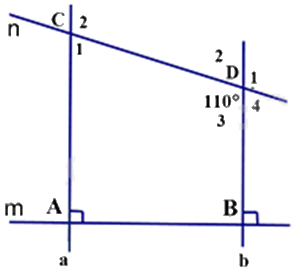
Cho hình vẽ bên, biết: \(m \bot a;m \bot b;\widehat {CDb} = {110^0}\).
a) Chứng minh: a // b
b) Tính số đo: \({\widehat {\rm{D}}_1}\) và \(\widehat {{\rm{ ACD}}}\)
(Học sinh vẽ lại hình vào bài làm)
Khẳng định nào sau đây sai:
Đáp án : D
Dựa vào kiến thức về số hữu tỉ.
+) \(0,\left( {001} \right) = \frac{1}{{999}} \in \mathbb{Q}\) nên A đúng.
+) \(\frac{7}{{33}} \in \mathbb{Q}\) nên B đúng.
+) \( - {\rm{ }}2\frac{3}{5} = - \frac{{13}}{5} \in \mathbb{Q}\) nên C đúng.
+) \(\sqrt 8 \) là số vô tỉ \( \Rightarrow \sqrt 8 \notin \mathbb{Q}\) nên D sai.
Số đối của \(\frac{5}{6}\) là:
Đáp án : D
Dựa vào khái niệm số đối.
Số đối của \(\frac{5}{6}\) là \( - \frac{5}{6}\).
Căn bậc hai số học của 196 là:
Đáp án : C
Sử dụng kiến thức về căn bậc hai số học: Căn bậc hai số học của số a không âm là số x không âm sao cho \({x^2} = a\).
Căn bậc hai số học của 196 là \(\sqrt {196} = 14\).
Số nào là số vô tỉ trong các số sau:
Đáp án : C
Số vô tỉ được biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn.
Ta có: \(\sqrt {\frac{1}{9}} = \frac{1}{3};0 = \frac{0}{1}\). Các số \(\frac{5}{{11}};\sqrt {\frac{1}{9}} ;0\) là số hữu tỉ nên không phải là số vô tỉ.
Vậy chỉ có \(\sqrt {12} \) là số vô tỉ.
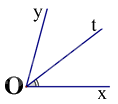
Cho \(\widehat {{\rm{xOy}}} = {70^0}\)và tia Ot là tia phân giác của \(\widehat {{\rm{xOy}}}\). Số đo \(\widehat {{\rm{xOt}}}\) bằng:
Đáp án : A
Dựa vào kiến thức về tia phân giác.
Vì Ot là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOt} = \widehat {tOy} = \frac{1}{2}\widehat {xOy} = \frac{1}{2}{.70^0} = {35^0}\).
Cho hình vẽ bên, biết \({\widehat {\rm{O}}_1} = {60^0}\). Số đo \({\widehat {\rm{O}}_3}\) là:
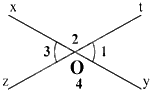
Đáp án : C
Góc \({O_1}\) và góc \({O_3}\) là hai góc đối đỉnh nên \(\widehat {{O_1}} = \widehat {{O_3}}\).
Vì góc \({O_1}\) và góc \({O_3}\) là hai góc đối đỉnh nên \(\widehat {{O_1}} = \widehat {{O_3}}\). Mà \(\widehat {{O_1}} = {60^0}\) nên \(\widehat {{O_3}} = {60^0}\).
Quan sát hình lăng trụ. ở hình bên. Hãy chọn câu đúng:
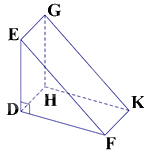
Đáp án : D
Dựa vào khái niệm hình lăng trụ.
Hình lăng trụ DEF.HGK có DEF và HGK là hai mặt đáy của hình lăng trụ nên chỉ có đáp án D đúng.
Hãy chọn câu sai. Hình lăng trụ đứng tứ giác có:
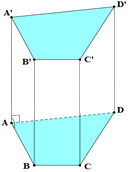
Đáp án : B
Quan sát hình vẽ để xác định.
Hình trên là hình lăng trụ đứng tứ giác nên hai mặt đáy song song với nhau nên A đúng.
Hai mặt đáy ABCD và A’B’C’D’ là hình tứ giác nên B sai, C đúng.
Các mặt bên của hình lăng trụ đứng tứ giác là hình chữ nhật nên D đúng.
Trong các dữ liệu sau, dữ liệu nào không phải là dữ liệu định lượng?
Đáp án : B
Dựa vào phân loại dữ liệu: Dữ liệu được chia thành hai loại: dữ liệu định tính và dữ liệu định lượng.
Trong các dữ liệu trên, chỉ có dữ liệu quốc tích của các học sinh trong trường quốc tế không phải là dữ liệu định lượng.
Theo số liệu biểu đồ hình quạt tròn ở hình bên thì tỉ lệ phần trăm đi xe đạp đến trường của các em học sinh ở một trường THCS là:
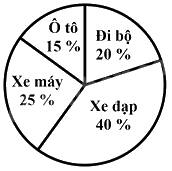
Đáp án : A
Quan sát biểu đồ để xác định.
Quan sát biểu đồ, tỉ lệ phần trăm học sinh đi xe đạp đến trường là 40%.
Kết quả tìm hiểu về sở thích chơi game của một số học sinh trong một trường
THCS được ghi bởi bảng thống kê sau. Hãy cho biết nhiều học sinh lựa chọn loại nào nhất?

Đáp án : A
Quan sát bảng thống kê, lập bảng số liệu biểu thị sở thích chơi game của các học sinh đó theo số lượng để biết học sinh lựa chọn loại nào nhiều nhất.
Ta có bảng số liệu sở thích chơi game của các học sinh theo số lượng như sau:
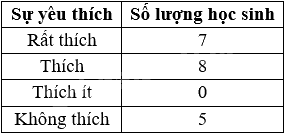
Quan sát bảng số liệu trên, ta thấy học sinh lựa chọn “Thích” có số lượng nhiều nhất.
Biểu đồ hình quạt tròn ở hình bên biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) xếp loại học lực giữa kì I của học sinh lớp 7A. Hỏi học sinh đạt loại gì là nhiều nhất?
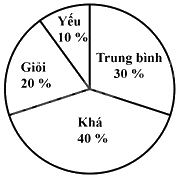
Đáp án : B
Quan sát biểu đồ để xác định.
Quan sát biểu đồ trên, ta thấy số học sinh khá chiếm tỉ lệ nhiều nhất (40%).
Thực hiện phép tính:
a) \({\left( {\frac{2}{3} - 1} \right)^2} - \frac{3}{5}:\frac{9}{{10}} + {1^{2022}}\).
b) \(\frac{8}{7} \cdot \left| {\frac{{ - 3}}{5}} \right| + \frac{8}{7} \cdot \sqrt {\frac{4}{{25}}} - \frac{{\sqrt 9 }}{4}\).
Sử dụng các quy tắc thực hiện phép tính.
a) \({\left( {\frac{2}{3} - 1} \right)^2} - \frac{3}{5}:\frac{9}{{10}} + {1^{2022}}\)
\(\begin{array}{l} = {\left( {\frac{2}{3} - \frac{3}{3}} \right)^2} - \frac{3}{5} \cdot \frac{{10}}{9} + 1\\ = {\left( {\frac{{ - 1}}{3}} \right)^2} - \frac{2}{3} + 1\\{\rm{ = }}\frac{1}{9} - \frac{6}{9} + \frac{9}{9}\\ = \frac{4}{9}\end{array}\)
b) \(\frac{8}{7} \cdot \left| {\frac{{ - 3}}{5}} \right| + \frac{8}{7} \cdot \sqrt {\frac{4}{{25}}} - \frac{{\sqrt 9 }}{4}\)
\(\begin{array}{l} = \frac{8}{7} \cdot \frac{3}{5} + \frac{8}{7} \cdot \frac{2}{5} - \frac{3}{4}\\ = \frac{8}{7} \cdot \left( {\frac{3}{5} + \frac{2}{5}} \right) - \frac{3}{4} = \frac{8}{7} \cdot 1 - \frac{3}{4}\\ = \frac{{32}}{{28}} - \frac{{21}}{{28}} = \frac{{11}}{{28}}\end{array}\)
Tìm x, biết:
a) \(x + 0,75 = \frac{2}{3}\).
b) \(\left| {\frac{1}{2} - x} \right| = \frac{4}{5}\).
a) Dựa vào quy tắc chuyển vế để tìm x.
b) Chia hai trường hợp: \(\frac{1}{2} - x = \frac{4}{5}\) hoặc \(\frac{1}{2} - x = \frac{{ - {\rm{ }}4}}{5}\).
a) \(x + 0,75 = \frac{2}{3}\)
\(\begin{array}{l}x + \frac{3}{4} = \frac{2}{3}\\x = \frac{2}{3} - \frac{3}{4}\\x = \frac{{ - 1}}{{12}}\end{array}\)
Vậy \(x = \frac{{ - 1}}{{12}}\).
b) \(\left| {\frac{1}{2} - x} \right| = \frac{4}{5}\) thì \(\frac{1}{2} - x = \frac{4}{5}\) hoặc \(\frac{1}{2} - x = \frac{{ - {\rm{ }}4}}{5}\).
TH1. \(\frac{1}{2} - x = \frac{4}{5}\)
\(\begin{array}{l}x = \frac{1}{2} - \frac{4}{5}\\x = \frac{{ - 3}}{{10}}\end{array}\)
TH2. \(\frac{1}{2} - x = \frac{{ - {\rm{ }}4}}{5}\)
\(\begin{array}{l}x = \frac{1}{2} + \frac{4}{5}\\x = \frac{{13}}{{10}}\end{array}\)
Vậy \(x \in \left\{ {\frac{{ - 3}}{{10}};\frac{{13}}{{10}}} \right\}\).
Diện tích nước Việt Nam là 331 698 km2. Hãy làm tròn diện tích này đến hàng nghìn.
Dựa vào cách làm tròn số với độ chính xác cho trước.
Ta có: 331 698 \( \approx \) 332 000.
Vậy diện tích nước Việt Nam được làm tròn đến hàng nghìn là khoảng 332 000 km2.
Một tủ gỗ có dạng hình hộp chữ nhật có kích thước: dài 70cm, rộng 60cm, cao 200cm như hình bên. Người ta muốn sơn tất cả các mặt của cây tủ trừ mặt tiếp giáp với mặt đất thì không sơn.

a) Tính diện tích xung quanh của cây tủ và tính diện tích phần cần sơn?
b) Chi phí để sơn mỗi m2 tủ là 100 000 đồng. Hỏi tổng chi phí để sơn là bao nhiêu?
a) Dựa vào công thức tính diện tích xung quanh của hình hộp chữ nhật.
Diện tích phần cần sơn là diện tích xung quanh + diện tích một đáy của tủ.
b) Chi phí sơn tủ = diện tích phần cần sơn . chi phí sơn mỗi m2 tủ. (nhớ đổi đơn vị m2).
a) Diện tích xung quanh của cây tủ là: (60 + 70).2.200 = 52 000 (cm2)
Diện tích phần cần sơn là: (60 + 70).2.200 + 60.70 = 52 000 + 4 200 = 56 200 (cm2)
b) Đổi: 56 200 (cm2) = 5,62 (m2)
Chi phí để sơn tất cả các mặt của cây tủ (trừ mặt tiếp giáp với mặt đất không sơn) là: 5,62 . 100 000 = 562 000 (đồng)
Cho hình vẽ bên, biết: \(m \bot a;m \bot b;\widehat {CDb} = {110^0}\).
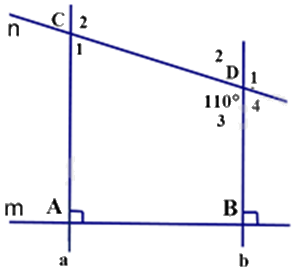
a) Chứng minh: a // b
b) Tính số đo: \({\widehat {\rm{D}}_1}\) và \(\widehat {{\rm{ ACD}}}\)
(Học sinh vẽ lại hình vào bài làm)
a) Chứng minh a và b cùng vuông góc với m nên song song với nhau.
b) Dựa vào kiến thức về hai góc đối, hai đường thẳng song song để tính số đo \({\widehat {\rm{D}}_1}\) và \(\widehat {{\rm{ ACD}}}\).
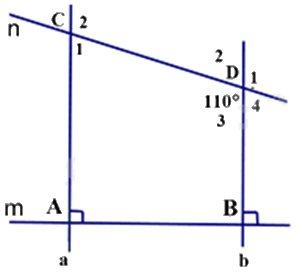
a) Vì \(m \bot a;m \bot b\) (gt) nên a // b (đpcm).
b) Ta có: \(\widehat {{D_1}} = \widehat {{D_3}} = {110^0}\) (hai góc đối đỉnh).
Ta có: a // b (cmt) suy ra:\({\rm{ }}{\widehat {\rm{C}}_2} = {\widehat {\rm{D}}_3} = {110^0}\)(2 góc so le trong)
Ta có:\({\rm{ }}{\widehat {\rm{C}}_2} + {\widehat {\rm{C}}_1} = {180^0}\) (2 góc kề bù)
\(\begin{array}{l}{110^0} + {\widehat {\rm{C}}_1} = {180^0}\\{\widehat {\rm{C}}_1} = {180^0} - {110^0} = {70^0}\end{array}\)
Vậy \(\widehat {{D_1}} = {110^0};\widehat {{C_1}} = {70^0}\).
Kỳ thi học kì 1 Toán 7 là một bước quan trọng trong quá trình học tập của học sinh. Việc chuẩn bị kỹ lưỡng không chỉ giúp học sinh đạt kết quả tốt mà còn tạo nền tảng vững chắc cho các kiến thức tiếp theo. Đề thi học kì 1 Toán 7 Chân trời sáng tạo - Đề số 11 do giaitoan.edu.vn cung cấp là một tài liệu ôn tập hữu ích, được thiết kế để giúp học sinh tự tin đối mặt với kỳ thi.
Đề thi này bao gồm các dạng bài tập thường gặp trong chương trình Toán 7 học kì 1, cụ thể:
Đề thi được chia thành các phần nhỏ, với mức độ khó tăng dần, giúp học sinh làm quen với các dạng bài tập khác nhau và rèn luyện kỹ năng giải quyết vấn đề.
Để giải đề thi này hiệu quả, học sinh cần nắm vững các kiến thức cơ bản và kỹ năng giải toán. Dưới đây là một số lời khuyên:
Bài 1: Giải phương trình sau: 2x + 5 = 11
Lời giải:
2x + 5 = 11
2x = 11 - 5
2x = 6
x = 3
Luyện tập thường xuyên là yếu tố then chốt để đạt kết quả tốt trong kỳ thi học kì 1 Toán 7. Học sinh nên giải nhiều đề thi khác nhau để làm quen với các dạng bài tập và rèn luyện kỹ năng giải toán. Ngoài ra, học sinh cũng nên tham khảo các tài liệu ôn tập, sách giáo khoa, và các trang web học toán online như giaitoan.edu.vn để bổ sung kiến thức và kỹ năng.
Hãy dành thời gian ôn tập và luyện tập thường xuyên để chuẩn bị tốt nhất cho kỳ thi học kì 1 Toán 7. Đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè nếu gặp khó khăn. Chúc các em học sinh đạt kết quả tốt nhất!
| Chủ đề | Tỷ lệ xuất hiện |
|---|---|
| Đại số | 30% |
| Hình học | 40% |
| Số học | 30% |