Chào mừng các em học sinh lớp 7 đến với đề thi học kì 1 môn Toán, đề số 10, chương trình Chân trời sáng tạo.
Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong học kì 1.
Giaitoan.edu.vn cung cấp đề thi với đáp án chi tiết, giúp các em tự học và nâng cao khả năng giải toán.
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I: Trắc nghiệm:
1.A | 2.A | 3.B | 4.D | 5.D | 6.D | 7.B | 8.D | 9.A | 10.B |
Câu 1
Phương pháp:
Số đối của số hữu tỉ \(a\) kí hiệu là \( - a\).
Cách giải:
Số đối của \(\dfrac{{ - 7}}{{12}}\) là: \( - \left( {\dfrac{{ - 7}}{{12}}} \right) = \dfrac{7}{{12}}\)
Chọn A.
Câu 2
Phương pháp:
Sử dụng phương pháp so sánh trung gian.
Cách giải:
+ Ta có: \(37 < 41\) nên \(\dfrac{{37}}{{41}} < 1\) suy ra \(\dfrac{{ - 37}}{{41}} > - 1\) (1)
\(23 > 17\) nên \(\dfrac{{23}}{{17}} > 1\) suy ra \(\dfrac{{23}}{{ - 17}} < - 1\) (2)
Từ (1) và (2), suy ra \(\dfrac{{23}}{{ - 17}} < - 1 < \dfrac{{ - 37}}{{41}}\), do đó, \(\dfrac{{ - 37}}{{41}} > \dfrac{{23}}{{ - 17}}\)
Vậy đáp án A đúng.
Chọn A.
Câu 3
Phương pháp:
Căn bậc hai số học của số \(a\) không âm là số \(x\) không âm sao cho \({x^2} = a\).
Sử dụng tính chất: \({x^2} = {\left( { - x} \right)^2}\)
Cách giải:
\(\sqrt {{{\left( { - \dfrac{2}{3}} \right)}^2}} = \sqrt {{{\left( {\dfrac{2}{3}} \right)}^2}} = \sqrt {\dfrac{4}{9}} = \dfrac{2}{3}\) nên đáp án A,C,D đúng
Do chỉ tồn tại căn bậc hai số học của một số không âm nên đáp án B sai.
Chọn B.
Câu 4
Phương pháp:
Vận dụng kiến thức giá trị tuyệt đối của một số thực, tìm phát biểu sai.
Cách giải:
Phát biểu A đúng vì giá trị tuyệt đối của một số thực là một số không âm.
Phát biểu B đúng vì hai số có giá trị tuyệt đối bằng nhau là hai số bằng nhau hoặc đối nhau.
Phát biểu C đúng vì hai số đối nhau có điểm biểu diễn cách đều điểm gốc 0 nên giá trị tuyệt đối của chúng bằng nhau.
Phát biểu D sai vì giá trị tuyệt đối của số âm là số đối của nó.
Chọn D.
Câu 5
Phương pháp:
Đọc biểu đồ quạt tròn, xác định tỉ lệ học sinh sử dụng internet cho từng mục đích
Cách giải:
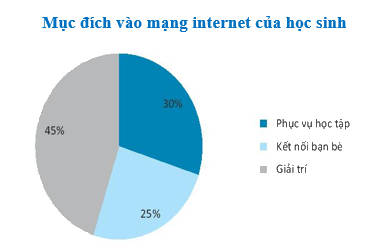
Tỉ lệ học sinh sử dụng internet:
+Phục vụ học tập là 40%
+Kết nối bạn bè là 25%
+Giải trí là 45%
Vậy % học sinh sử dụng internet không phục vụ học tập là: 25%+45%=70%
Chọn D.
Câu 6
Phương pháp:
Đọc biểu đồ đoạn thẳng
Cách giải:
Năm 2021 tỉ lệ học sinh THCS nghiện điện thoại di động là cao nhất (15%).
Chọn D.
Câu 7
Phương pháp:
Thể tích của hình hộp chữ nhật có chiều dài đáy là \(a\), chiều rộng đáy là \(b\) và chiều cao là \(c:V = abc\)
Thể tích của hình lập phương có một cạnh là \(a:V = {a^3}\)
Cách giải:
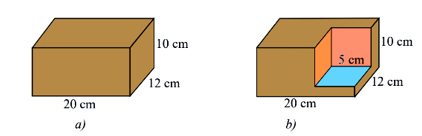
Thể tích ban đầu của khối gỗ là: \({V_1} = 20.12.10 = 2400\,\left( {c{m^3}} \right)\)
Thể tích phần khối gỗ cắt bỏ đi là: \({V_2} = {5^3} = 125\,\left( {c{m^3}} \right)\)
Thể tích phần còn lại của khối gỗ là: \(V = {V_1} - {V_2} = 2400 - 125 = 2275\,\left( {c{m^3}} \right)\)
Chọn B.
Câu 8
Phương pháp:
Hình lăng trụ đứng tứ giác là hình có hai mặt đáy cùng là tứ giác và song song với nhau; các mặt bên đều là hình chữ nhật; các cạnh bên bằng nhau.
Cách giải:
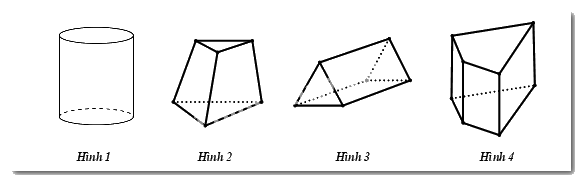
Trong 4 hình vẽ, ta nhận thấy Hình 4 là hình lăng trụ đứng tứ giác.
Chọn D.
Câu 9
Phương pháp:
Định lí là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … thì ….
Cách giải:
Phát biểu định lí: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
Chọn A.
Câu 10
Phương pháp
\(Oz\) là tia phân giác của \(\angle xOy\) thì ta có: \(\angle xOz = \angle zOy = \dfrac{{\angle xOy}}{2}\)
\(\angle xOz\) và \(\angle zOy\) là hai góc kề nhau thì ta có: \(\angle xOz + \angle zOy = \angle xOy\).
\(\angle xOz\) và \(\angle zOy\) là hai góc kề bù thì ta có: \(\angle xOy = \angle xOz + \angle zOy = {180^0}\)
Cách giải:
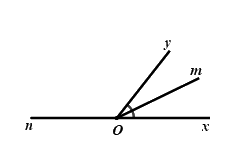
Vì \(Om\) là tia phân giác của \(\angle xOy\) nên \(\angle mOy = \dfrac{{\angle xOy}}{2} = \dfrac{{{{50}^0}}}{2} = {25^0}\)
Ta có: \(\angle nOy\) và \(\angle yOx\) là hai góc kề bù nên \(\angle nOy + \angle yOx = {180^0}\)
\(\begin{array}{l} \Rightarrow \angle nOy + {50^0} = {180^0}\\ \Rightarrow \angle nOy = {180^0} - {50^0} = {130^0}\end{array}\)
Ta có: \(\angle nOy\) và \(\angle yOm\) là hai góc kề nhau nên \(\angle nOy + \angle yOm = \angle nOm\)
\( \Rightarrow {130^0} + {25^0} = {155^0} = \angle nOm\)
Vậy \(\angle mOn = {155^0}\)
Chọn B.
Phần II. Tự luận (7 điểm):
Bài 1
Phương pháp:
a) Đổi số thập phân sang phân số
Thực hiện các phép toán với số hữu tỉ.
b) Lũy thừa của một số hữu tỉ: \({\left( {\dfrac{a}{b}} \right)^n} = \dfrac{{{a^n}}}{{{b^n}}}\,\,\left( {b \ne 0;n \in \mathbb{Z}} \right)\)
Thực hiện các phép toán với số hữu tỉ.
c) Tính căn bậc hai số học của một số thực
Thực hiện các phép toán với số hữu tỉ.
d) Lũy thừa của một số hữu tỉ: \({\left( {\dfrac{a}{b}} \right)^n} = \dfrac{{{a^n}}}{{{b^n}}}\,\,\left( {b \ne 0;n \in \mathbb{Z}} \right)\)
Tính căn bậc hai số học của một số thực
Vận dụng kiến thức giá trị tuyệt đối của một số thực: \(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,\,\,\,khi\,\,\,x > 0\\ - x\,\,\,khi\,\,x < 0\\0\,\,\,\,\,\,\,khi\,\,\,x = 0\end{array} \right.\)
Thực hiện các phép toán với số hữu tỉ.
Cách giải:
a) \(\dfrac{2}{9} + \dfrac{1}{3}:\left( { - \dfrac{3}{2}} \right) + \dfrac{1}{2}.{\left( { - 0,5} \right)^0}\)
\(\begin{array}{l} = \dfrac{2}{9} + \dfrac{1}{3}.\left( {\dfrac{{ - 2}}{3}} \right) + \dfrac{1}{2}.1\\ = \dfrac{2}{9} + \dfrac{{ - 2}}{9} + \dfrac{1}{2}\\ = 0 + \dfrac{1}{2}\\ = \dfrac{1}{2}\end{array}\)
b) \({\left( {\dfrac{{ - 1}}{2}} \right)^2} - \dfrac{5}{8}:{\left( {0,5} \right)^3} - \dfrac{5}{3}.\left( { - 6} \right)\)
\(\begin{array}{l} = \dfrac{{{{\left( { - 1} \right)}^2}}}{{{2^2}}} - \dfrac{5}{8}:{\left( {\dfrac{1}{2}} \right)^3} - 5.\left( { - 2} \right)\\ = \dfrac{1}{4} - \dfrac{5}{8}:\dfrac{{{1^3}}}{{{2^3}}} - \left( { - 10} \right)\\ = \dfrac{1}{4} - \dfrac{5}{8}:\dfrac{1}{8} + 10\\ = \dfrac{1}{4} - \dfrac{5}{8}.\dfrac{8}{1} + 10\\ = \dfrac{1}{4} - 5 + 10 = \dfrac{1}{4} + 5\\ = \dfrac{1}{4} + \dfrac{{20}}{4} = \dfrac{{21}}{4}\end{array}\)
c) \(\sqrt {0,04} + \sqrt {0,25} + 2,31\)
\(\begin{array}{l} = \sqrt {{{\left( {0,2} \right)}^2}} + \sqrt {{{\left( {0,5} \right)}^2}} + 2,31\\ = 0,2 + 0,5 + 2,31\\ = 3,01\end{array}\)
d) \(\left| {\sqrt {169} - \sqrt {900} } \right| - \left| {\dfrac{{ - 5}}{4}} \right|:{\left( {\dfrac{1}{3} - \dfrac{1}{2}} \right)^2}\)
\(\begin{array}{l} = \left| {\sqrt {{{13}^2}} - \sqrt {{{30}^2}} } \right| - \dfrac{5}{4}:{\left( {\dfrac{2}{6} - \dfrac{3}{6}} \right)^2}\\ = \left| {13 - 30} \right| - \dfrac{5}{4}:{\left( {\dfrac{1}{6}} \right)^2}\\ = \left| { - 17} \right| - \dfrac{5}{4}:\dfrac{1}{{36}}\\ = 17 - \dfrac{5}{4}.36\\ = 17 - 45\\ = - 28\end{array}\)
Bài 2
Phương pháp:
a) Thực hiện các phép toán với số hữu tỉ
Vận dụng quy tắc chuyển vế, tìm \(x\).
b) Giải \({\left[ {A\left( x \right)} \right]^2} = {a^2} = {\left( { - a} \right)^2}\)
Trường hợp 1: \(A\left( x \right) = a\)
Trường hợp 2: \(A\left( x \right) = - a\)
c) Tính căn bậc hai số học của số thực
Thực hiện các phép toán với số hữu tỉ
Vận dụng quy tắc chuyển vế, tìm \(x\).
d) \(\left| x \right| = a\)
Trường hợp \(a < 0\), khi đó phương trình không có nghiệm \(x\)
Trường hợp \(a > 0\), vận dụng kiến thức giá trị tuyệt đối của một số thực: \(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,\,\,\,khi\,\,\,x > 0\\ - x\,\,\,khi\,\,x < 0\\0\,\,\,\,\,\,\,khi\,\,\,x = 0\end{array} \right.\)
Cách giải:
a) \(\dfrac{1}{3}x + \dfrac{2}{5}\left( {x - 1} \right) = 0\)
\(\begin{array}{l}\dfrac{1}{3}x + \dfrac{2}{5}x - \dfrac{2}{5} = 0\\x.\left( {\dfrac{1}{3} + \dfrac{2}{5}} \right) = \dfrac{2}{5}\\x.\left( {\dfrac{5}{{15}} + \dfrac{6}{{15}}} \right) = \dfrac{2}{5}\\x.\dfrac{{11}}{{15}} = \dfrac{2}{5}\\x = \dfrac{2}{5}:\dfrac{{11}}{{15}}\\x = \dfrac{2}{5}.\dfrac{{15}}{{11}}\\x = \dfrac{6}{{11}}\end{array}\)
Vậy \(x = \dfrac{6}{{11}}\)
b) \({\left( {2x + 1} \right)^2} = \dfrac{{36}}{{25}}\)
\({\left( {2x + 1} \right)^2} = {\left( {\dfrac{6}{5}} \right)^2} = {\left( { - \dfrac{6}{5}} \right)^2}\)
Trường hợp 1:
\(\begin{array}{l}2x + 1 = \dfrac{6}{5}\\2x = \dfrac{6}{5} - 1 = \dfrac{6}{5} - \dfrac{5}{5}\\2x = \dfrac{1}{5}\\x = \dfrac{1}{5}:2 = \dfrac{1}{5}.\dfrac{1}{2}\\x = \dfrac{1}{{10}}\end{array}\)
Vậy \(x \in \left\{ {\dfrac{1}{{10}};\dfrac{{ - 11}}{{10}}} \right\}\)
Trường hợp 2:
\(\begin{array}{l}2x + 1 = - \dfrac{6}{5}\\2x = \dfrac{{ - 6}}{5} - 1 = \dfrac{{ - 6}}{5} - \dfrac{5}{5}\\2x = \dfrac{{ - 11}}{5}\\x = \dfrac{{ - 11}}{5}:2 = \dfrac{{ - 11}}{5}.\dfrac{1}{2}\\x = \dfrac{{ - 11}}{{10}}\end{array}\)
c) \(\dfrac{1}{2}x + \sqrt {0,04} = \sqrt {1,96} \)
\(\begin{array}{l}\dfrac{1}{2}x + \sqrt {{{\left( {0,2} \right)}^2}} = \sqrt {{{\left( {1,4} \right)}^2}} \\\dfrac{1}{2}x + 0,2 = 1,4\\\dfrac{1}{2}x = 1,4 - 0,2 = 1,2\\x = 1,2:\dfrac{1}{2} = 1,2.2\\x = 2,4\end{array}\)
Vậy \(x = 2,4\).
d) \(\left| {\left| {2x - 1} \right| + \dfrac{1}{2}} \right| = \dfrac{4}{5}\)
Trường hợp 1:
\(\begin{array}{l}\left| {2x - 1} \right| + \dfrac{1}{2} = \dfrac{4}{5}\\\left| {2x - 1} \right| = \dfrac{4}{5} - \dfrac{1}{2} = \dfrac{8}{{10}} - \dfrac{5}{{10}}\\\left| {2x - 1} \right| = \dfrac{3}{{10}}\end{array}\)
*\(2x - 1 = \dfrac{3}{{10}}\)
\(\begin{array}{l}2x = \dfrac{3}{{10}} + 1 = \dfrac{3}{{10}} + \dfrac{{10}}{{10}}\\2x = \dfrac{{13}}{{10}}\\x = \dfrac{{13}}{{10}}:2 = \dfrac{{13}}{{10}}.\dfrac{1}{2}\\x = \dfrac{{13}}{{20}}\end{array}\)
*\(2x - 1 = \dfrac{{ - 3}}{{10}}\)
\(\begin{array}{l}2x = \dfrac{{ - 3}}{{10}} + 1 = \dfrac{{ - 3}}{{10}} + \dfrac{{10}}{{10}}\\2x = \dfrac{7}{{10}}\\x = \dfrac{7}{{10}}:2 = \dfrac{7}{{10}}.\dfrac{1}{2}\\x = \dfrac{7}{{20}}\end{array}\)
Trường hợp 2:
\(\begin{array}{l}\left| {2x - 1} \right| + \dfrac{1}{2} = - \dfrac{4}{5}\\\left| {2x - 1} \right| = - \dfrac{4}{5} - \dfrac{1}{2} = \dfrac{{ - 8}}{{10}} - \dfrac{5}{{10}}\\\left| {2x - 1} \right| = \dfrac{{ - 13}}{{10}}\end{array}\)
Vì \(\dfrac{{ - 13}}{{10}} < 0\) nên không có \(x\) thỏa mãn \(\left| {2x - 1} \right| = \dfrac{{ - 13}}{{10}}\).
Vậy \(x \in \left\{ {\dfrac{{13}}{{20}};\dfrac{7}{{20}}} \right\}\)
Bài 3
Phương pháp:
Áp dụng tính chất hai đường thẳng song song, tiên đề Ơ-Clit.
Tính chất: Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau.
Cách giải:
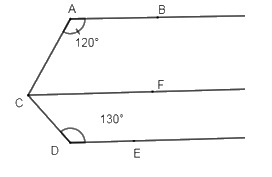
Kẻ \(CF//\,AB \Rightarrow \widehat {BAC} + \widehat {ACF} = {180^0}\) (2 góc trong cùng phía)
\( \Rightarrow \widehat {ACF} = {180^0} - \widehat {BAC} = {180^0} - {120^0} = {60^0}\)
Ta có: \(\left\{ \begin{array}{l}AB//\,DE\\CF//\,AB\end{array} \right.\left( {gt} \right) \Rightarrow DE//\,CF.\)
\( \Rightarrow \widehat {FCD} + \widehat {C{\rm{D}}E} = {180^0}\) (2 góc trong cùng phía)
\(\begin{array}{l} \Rightarrow \widehat {DCF} = {180^0} - \widehat {C{\rm{D}}E} = {180^0} - {130^0} = {50^0}\\ \Rightarrow \widehat {AC{\rm{D}}} = \widehat {ACF} + \widehat {FC{\rm{D}}} = {60^0} + {50^0} = {110^0}\\ \Rightarrow \widehat {BAC} + \widehat {AC{\rm{D}}} + \widehat {C{\rm{D}}E} = {120^0} + {110^0} + {130^0} = {360^0}\end{array}\)
Bài 4
Phương pháp:
a) Thể tích của hình lăng trụ đứng tam giác: \(V = S\)đáy\(.h\)
Trong đó: \(V:\) thể tích của hình lăng trụ đứng tam giác
\(S\)đáy: diện tích một đáy của hình lăng trụ đứng tam giác
\(h\): chiều cao của hình lăng trụ đứng tam giác
b) Diện tích xung quanh của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác: \({S_{xq}} = C\)đáy.\(h\)
Trong đó: \({S_{xq}}:\) diện tích xung quanh hình lăng trụ đứng tam giác
\(C\)đáy: diện tích một đáy của hình lăng trụ đứng tam giác
\(h\): chiều cao của hình lăng trụ đứng tam giác
Chi phí làm hộp = (diện tích xung quanh + diện tích hai đáy) . giá tiền 1 mét vuông bìa
Cách giải:
a) Đáy của hình lăng trụ tam giác là một tam giác vuông nên diện tích đáy là: \(S\)đáy\( = \)\(\dfrac{1}{2}.9.12 = 54\,\left( {c{m^2}} \right)\)
Thể tích cái bánh là: \(V = S\)đáy\(.h = 54.5 = 270\,\left( {c{m^3}} \right)\)
b) Chu vi đáy của cái bánh là: \(C = 9 + 12 + 15 = 36\,\left( {cm} \right)\)
Diện tích xung quanh của cái bánh là: \({S_{xq}} = C.h = 36.5 = 180\,\left( {c{m^2}} \right)\)
Diện tích hai đáy của cái bánh là: \(S = 2.54 = 108\,\left( {c{m^2}} \right)\)
Diện tích làm hộp của cái bánh là: \({S_{xq}} + S = 180 + 108 = 288\left( {c{m^2}} \right) = 0,0288\,\left( {{m^2}} \right)\)
Chi phí làm hộp là: \(0,0288.22500 = 648\) (đồng)
Bài 5
Phương pháp:
Đánh giá các số hạng của tổng để tìm giá trị nhỏ nhất của \(A\).
Chú ý: \({x^2} \ge 0,\forall x \in \mathbb{R}\).
Cách giải:
Ta có: \({x^2} \ge 0;\sqrt x \ge 0\) với mọi số thực \(x \ge 0\) nên \({x^2} + \sqrt x \ge 0\) với mọi số thực \(x \ge 0\).
Suy ra \({x^2} + \sqrt x - 113 \ge - 113\) với mọi số thực \(x \ge 0.\) Hay \(A \ge - 113\) với mọi số thực \(x \ge 0.\)
Dấu “=” xảy ra \( \Leftrightarrow x = 0\).
Vậy \(\min A = - 113 \Leftrightarrow x = 0\).
8.D | 10.B |
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Số đối của \(\dfrac{{ - 7}}{{12}}\) là:
A. \(\dfrac{7}{{12}}\)
B. \(\dfrac{7}{{ - 12}}\)
C. \(\dfrac{{12}}{{ - 7}}\)
D. \(\dfrac{{12}}{7}\)
Câu 2: Chọn khẳng định đúng.
A. \(\dfrac{{ - 37}}{{41}} > \dfrac{{23}}{{ - 17}}\)
B. \({\left( {\dfrac{1}{3}} \right)^{12}} > {\left( {\dfrac{1}{3}} \right)^{10}}\)
C. \({\left( {2,5} \right)^6} = {\left( {0,5} \right)^{12}}\)
D. \({\left( {2,5} \right)^4} < {\left( { - 2,5} \right)^5}\)
Câu 3: Chọn đáp án sai. Nếu \(\sqrt x = \dfrac{2}{3}\) thì:
A. \(x = {\left( { - \dfrac{2}{3}} \right)^2}\)
B. \(x = - {\left( { - \dfrac{2}{3}} \right)^2}\)
C. \(x = \dfrac{4}{9}\)
D. \(x = {\left( {\dfrac{2}{3}} \right)^2}\)
Câu 4: Trong các phát biểu sau, phát biểu nào sai?
A. Giá trị tuyệt đối của một số thực là một số dương hoặc bằng 0.
B. Hai số có giá trị tuyệt đối bằng nhau là hai số bằng nhau hoặc đối nhau.
C. Hai số đối nhau có giá trị tuyệt đối bằng nhau.
D. Giá trị tuyệt đối của một số thực luôn bằng chính nó.
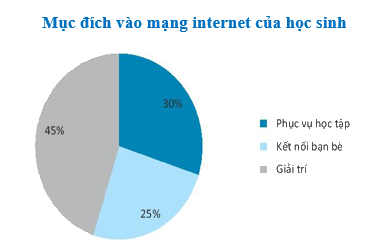
Câu 5: Căn cứ vào biểu đồ sau đây, hãy xác định bao nhiêu % học sinh THCS sử dụng internet KHÔNG phục vụ học tập?
A. \(30.\)
B. \(45.\)
C. \(25.\)
D. \(70.\)
Câu 6: Cho biểu đồ sau:
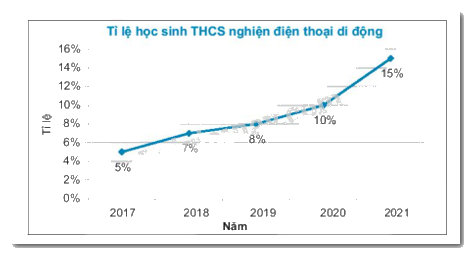
Năm nào có tỉ lệ học sinh THCS nghiện điện thoại cao nhất?
A. 2018.
B. 2019.
C. 2020.
D. 2021.
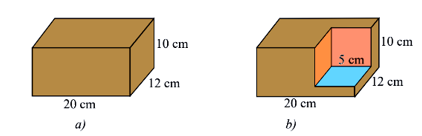
Câu 7: Một khối gỗ dạng hình hộp chữ nhật có kịch thước như Hình a). Người ta cắt đi một phần khối gỗ có dạng hình lập phương cạnh 5 cm. Tính thể tích phần còn lại của khối gỗ (Hình b).
A. \(1888c{m^3}\)
B. \(2275\,c{m^3}\)
C. \(2144c{m^3}\)
D. \(2300c{m^3}\)
Câu 8: Trong các hình sau, hình nào là hình lăng trụ đứng tứ giác?
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Câu 9: Phát biểu định lí sau bằng lời:
GT | \(a//b,c \bot a\) |
KL | \(c \bot b\) |
A. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
B. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó song song với đường thẳng kia.
C. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó tạo với đường thẳng kia một góc \({60^0}\).
D. Cả A, B, C đều đúng.
Câu 10: Vẽ \(\angle xOy = {50^0}\). Vẽ tia \(Om\) là tia phân giác của góc \(xOy\). Vẽ tia \(On\) là tia đối của tia \(Ox\). Tính góc \(mOn\).
A. \(\angle mOn = {125^0}\)
B. \(\angle mOn = {155^0}\)
C. \(\angle mOn = {160^0}\)
D. \(\angle mOn = {175^0}\)
Phần II. Tự luận (7 điểm):
Bài 1: (2,0 điểm)
Thực hiện phép tính:
a) \(\dfrac{2}{9} + \dfrac{1}{3}:\left( { - \dfrac{3}{2}} \right) + \dfrac{1}{2}.{\left( { - 0,5} \right)^0}\)
b) \({\left( {\dfrac{{ - 1}}{2}} \right)^2} - \dfrac{5}{8}:{\left( {0,5} \right)^3} - \dfrac{5}{3}.\left( { - 6} \right)\)
c) \(\sqrt {0,04} + \sqrt {0,25} + 2,31\)
d) \(\left| {\sqrt {169} - \sqrt {900} } \right| - \left| {\dfrac{{ - 5}}{4}} \right|:{\left( {\dfrac{1}{3} - \dfrac{1}{2}} \right)^2}\)
Bài 2: (2,0 điểm)
Tìm \(x\), biết:
a) \(\dfrac{1}{3}x + \dfrac{2}{5}\left( {x - 1} \right) = 0\)
b) \({\left( {2x + 1} \right)^2} = \dfrac{{36}}{{25}}\)
c) \(\dfrac{1}{2}x + \sqrt {0,04} = \sqrt {1,96} \)
d) \(\left| {\left| {2x - 1} \right| + \dfrac{1}{2}} \right| = \dfrac{4}{5}\)
Bài 3: (1,0 điểm)
Cho hình vẽ sau:
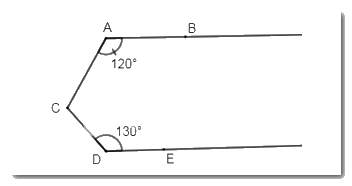
Biết \(AB//\,DE,\,\widehat {BAC} = {120^0},\,\widehat {CDE} = {130^0}.\) Tính: \(\widehat {BAC} + \widehat {AC{\rm{D}}} + \widehat {C{\rm{D}}E}\).
Bài 4: (1,5 điểm)
Một chiếc bánh ngọt có dạng hình lăng trụ đứng tam giác, có kích thước như hình vẽ bên dưới.
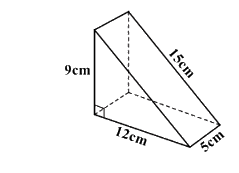
a) Tính thể tích cái bánh.
b) Nếu phải làm một chiếc hộp để đựng vừa khít cái bánh này thì chi phí làm hộp là bao nhiêu biết giá 1 mét vuông bìa là 22500 đồng.
Bài 5: (0,5 điểm)
Tìm giá trị nhỏ nhất của biểu thức \(A = {x^2} + \sqrt x - 113\) với \(x \ge 0\).
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Số đối của \(\dfrac{{ - 7}}{{12}}\) là:
A. \(\dfrac{7}{{12}}\)
B. \(\dfrac{7}{{ - 12}}\)
C. \(\dfrac{{12}}{{ - 7}}\)
D. \(\dfrac{{12}}{7}\)
Câu 2: Chọn khẳng định đúng.
A. \(\dfrac{{ - 37}}{{41}} > \dfrac{{23}}{{ - 17}}\)
B. \({\left( {\dfrac{1}{3}} \right)^{12}} > {\left( {\dfrac{1}{3}} \right)^{10}}\)
C. \({\left( {2,5} \right)^6} = {\left( {0,5} \right)^{12}}\)
D. \({\left( {2,5} \right)^4} < {\left( { - 2,5} \right)^5}\)
Câu 3: Chọn đáp án sai. Nếu \(\sqrt x = \dfrac{2}{3}\) thì:
A. \(x = {\left( { - \dfrac{2}{3}} \right)^2}\)
B. \(x = - {\left( { - \dfrac{2}{3}} \right)^2}\)
C. \(x = \dfrac{4}{9}\)
D. \(x = {\left( {\dfrac{2}{3}} \right)^2}\)
Câu 4: Trong các phát biểu sau, phát biểu nào sai?
A. Giá trị tuyệt đối của một số thực là một số dương hoặc bằng 0.
B. Hai số có giá trị tuyệt đối bằng nhau là hai số bằng nhau hoặc đối nhau.
C. Hai số đối nhau có giá trị tuyệt đối bằng nhau.
D. Giá trị tuyệt đối của một số thực luôn bằng chính nó.
Câu 5: Căn cứ vào biểu đồ sau đây, hãy xác định bao nhiêu % học sinh THCS sử dụng internet KHÔNG phục vụ học tập?
A. \(30.\)
B. \(45.\)
C. \(25.\)
D. \(70.\)
Câu 6: Cho biểu đồ sau:
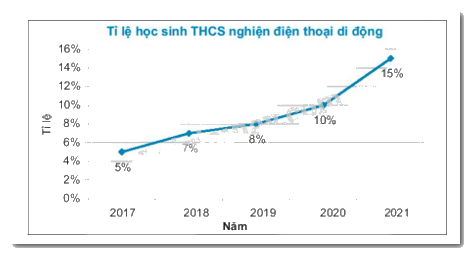
Năm nào có tỉ lệ học sinh THCS nghiện điện thoại cao nhất?
A. 2018.
B. 2019.
C. 2020.
D. 2021.
Câu 7: Một khối gỗ dạng hình hộp chữ nhật có kịch thước như Hình a). Người ta cắt đi một phần khối gỗ có dạng hình lập phương cạnh 5 cm. Tính thể tích phần còn lại của khối gỗ (Hình b).
A. \(1888c{m^3}\)
B. \(2275\,c{m^3}\)
C. \(2144c{m^3}\)
D. \(2300c{m^3}\)
Câu 8: Trong các hình sau, hình nào là hình lăng trụ đứng tứ giác?
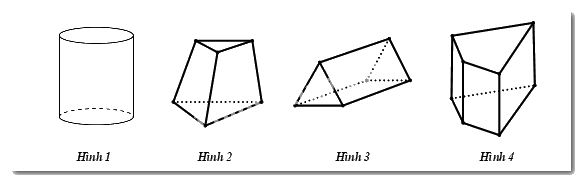
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Câu 9: Phát biểu định lí sau bằng lời:
GT | \(a//b,c \bot a\) |
KL | \(c \bot b\) |
A. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
B. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó song song với đường thẳng kia.
C. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó tạo với đường thẳng kia một góc \({60^0}\).
D. Cả A, B, C đều đúng.
Câu 10: Vẽ \(\angle xOy = {50^0}\). Vẽ tia \(Om\) là tia phân giác của góc \(xOy\). Vẽ tia \(On\) là tia đối của tia \(Ox\). Tính góc \(mOn\).
A. \(\angle mOn = {125^0}\)
B. \(\angle mOn = {155^0}\)
C. \(\angle mOn = {160^0}\)
D. \(\angle mOn = {175^0}\)
Phần II. Tự luận (7 điểm):
Bài 1: (2,0 điểm)
Thực hiện phép tính:
a) \(\dfrac{2}{9} + \dfrac{1}{3}:\left( { - \dfrac{3}{2}} \right) + \dfrac{1}{2}.{\left( { - 0,5} \right)^0}\)
b) \({\left( {\dfrac{{ - 1}}{2}} \right)^2} - \dfrac{5}{8}:{\left( {0,5} \right)^3} - \dfrac{5}{3}.\left( { - 6} \right)\)
c) \(\sqrt {0,04} + \sqrt {0,25} + 2,31\)
d) \(\left| {\sqrt {169} - \sqrt {900} } \right| - \left| {\dfrac{{ - 5}}{4}} \right|:{\left( {\dfrac{1}{3} - \dfrac{1}{2}} \right)^2}\)
Bài 2: (2,0 điểm)
Tìm \(x\), biết:
a) \(\dfrac{1}{3}x + \dfrac{2}{5}\left( {x - 1} \right) = 0\)
b) \({\left( {2x + 1} \right)^2} = \dfrac{{36}}{{25}}\)
c) \(\dfrac{1}{2}x + \sqrt {0,04} = \sqrt {1,96} \)
d) \(\left| {\left| {2x - 1} \right| + \dfrac{1}{2}} \right| = \dfrac{4}{5}\)
Bài 3: (1,0 điểm)
Cho hình vẽ sau:
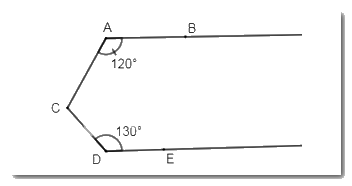
Biết \(AB//\,DE,\,\widehat {BAC} = {120^0},\,\widehat {CDE} = {130^0}.\) Tính: \(\widehat {BAC} + \widehat {AC{\rm{D}}} + \widehat {C{\rm{D}}E}\).
Bài 4: (1,5 điểm)
Một chiếc bánh ngọt có dạng hình lăng trụ đứng tam giác, có kích thước như hình vẽ bên dưới.
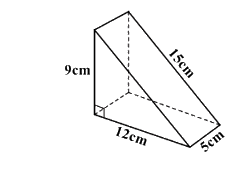
a) Tính thể tích cái bánh.
b) Nếu phải làm một chiếc hộp để đựng vừa khít cái bánh này thì chi phí làm hộp là bao nhiêu biết giá 1 mét vuông bìa là 22500 đồng.
Bài 5: (0,5 điểm)
Tìm giá trị nhỏ nhất của biểu thức \(A = {x^2} + \sqrt x - 113\) với \(x \ge 0\).
Phần I: Trắc nghiệm:
1.A | 2.A | 3.B | 4.D | 5.D | 6.D | 7.B | 8.D | 9.A | 10.B |
Câu 1
Phương pháp:
Số đối của số hữu tỉ \(a\) kí hiệu là \( - a\).
Cách giải:
Số đối của \(\dfrac{{ - 7}}{{12}}\) là: \( - \left( {\dfrac{{ - 7}}{{12}}} \right) = \dfrac{7}{{12}}\)
Chọn A.
Câu 2
Phương pháp:
Sử dụng phương pháp so sánh trung gian.
Cách giải:
+ Ta có: \(37 < 41\) nên \(\dfrac{{37}}{{41}} < 1\) suy ra \(\dfrac{{ - 37}}{{41}} > - 1\) (1)
\(23 > 17\) nên \(\dfrac{{23}}{{17}} > 1\) suy ra \(\dfrac{{23}}{{ - 17}} < - 1\) (2)
Từ (1) và (2), suy ra \(\dfrac{{23}}{{ - 17}} < - 1 < \dfrac{{ - 37}}{{41}}\), do đó, \(\dfrac{{ - 37}}{{41}} > \dfrac{{23}}{{ - 17}}\)
Vậy đáp án A đúng.
Chọn A.
Câu 3
Phương pháp:
Căn bậc hai số học của số \(a\) không âm là số \(x\) không âm sao cho \({x^2} = a\).
Sử dụng tính chất: \({x^2} = {\left( { - x} \right)^2}\)
Cách giải:
\(\sqrt {{{\left( { - \dfrac{2}{3}} \right)}^2}} = \sqrt {{{\left( {\dfrac{2}{3}} \right)}^2}} = \sqrt {\dfrac{4}{9}} = \dfrac{2}{3}\) nên đáp án A,C,D đúng
Do chỉ tồn tại căn bậc hai số học của một số không âm nên đáp án B sai.
Chọn B.
Câu 4
Phương pháp:
Vận dụng kiến thức giá trị tuyệt đối của một số thực, tìm phát biểu sai.
Cách giải:
Phát biểu A đúng vì giá trị tuyệt đối của một số thực là một số không âm.
Phát biểu B đúng vì hai số có giá trị tuyệt đối bằng nhau là hai số bằng nhau hoặc đối nhau.
Phát biểu C đúng vì hai số đối nhau có điểm biểu diễn cách đều điểm gốc 0 nên giá trị tuyệt đối của chúng bằng nhau.
Phát biểu D sai vì giá trị tuyệt đối của số âm là số đối của nó.
Chọn D.
Câu 5
Phương pháp:
Đọc biểu đồ quạt tròn, xác định tỉ lệ học sinh sử dụng internet cho từng mục đích
Cách giải:
Tỉ lệ học sinh sử dụng internet:
+Phục vụ học tập là 40%
+Kết nối bạn bè là 25%
+Giải trí là 45%
Vậy % học sinh sử dụng internet không phục vụ học tập là: 25%+45%=70%
Chọn D.
Câu 6
Phương pháp:
Đọc biểu đồ đoạn thẳng
Cách giải:
Năm 2021 tỉ lệ học sinh THCS nghiện điện thoại di động là cao nhất (15%).
Chọn D.
Câu 7
Phương pháp:
Thể tích của hình hộp chữ nhật có chiều dài đáy là \(a\), chiều rộng đáy là \(b\) và chiều cao là \(c:V = abc\)
Thể tích của hình lập phương có một cạnh là \(a:V = {a^3}\)
Cách giải:
Thể tích ban đầu của khối gỗ là: \({V_1} = 20.12.10 = 2400\,\left( {c{m^3}} \right)\)
Thể tích phần khối gỗ cắt bỏ đi là: \({V_2} = {5^3} = 125\,\left( {c{m^3}} \right)\)
Thể tích phần còn lại của khối gỗ là: \(V = {V_1} - {V_2} = 2400 - 125 = 2275\,\left( {c{m^3}} \right)\)
Chọn B.
Câu 8
Phương pháp:
Hình lăng trụ đứng tứ giác là hình có hai mặt đáy cùng là tứ giác và song song với nhau; các mặt bên đều là hình chữ nhật; các cạnh bên bằng nhau.
Cách giải:
Trong 4 hình vẽ, ta nhận thấy Hình 4 là hình lăng trụ đứng tứ giác.
Chọn D.
Câu 9
Phương pháp:
Định lí là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … thì ….
Cách giải:
Phát biểu định lí: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
Chọn A.
Câu 10
Phương pháp
\(Oz\) là tia phân giác của \(\angle xOy\) thì ta có: \(\angle xOz = \angle zOy = \dfrac{{\angle xOy}}{2}\)
\(\angle xOz\) và \(\angle zOy\) là hai góc kề nhau thì ta có: \(\angle xOz + \angle zOy = \angle xOy\).
\(\angle xOz\) và \(\angle zOy\) là hai góc kề bù thì ta có: \(\angle xOy = \angle xOz + \angle zOy = {180^0}\)
Cách giải:
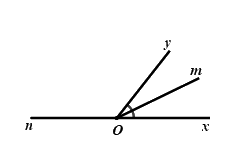
Vì \(Om\) là tia phân giác của \(\angle xOy\) nên \(\angle mOy = \dfrac{{\angle xOy}}{2} = \dfrac{{{{50}^0}}}{2} = {25^0}\)
Ta có: \(\angle nOy\) và \(\angle yOx\) là hai góc kề bù nên \(\angle nOy + \angle yOx = {180^0}\)
\(\begin{array}{l} \Rightarrow \angle nOy + {50^0} = {180^0}\\ \Rightarrow \angle nOy = {180^0} - {50^0} = {130^0}\end{array}\)
Ta có: \(\angle nOy\) và \(\angle yOm\) là hai góc kề nhau nên \(\angle nOy + \angle yOm = \angle nOm\)
\( \Rightarrow {130^0} + {25^0} = {155^0} = \angle nOm\)
Vậy \(\angle mOn = {155^0}\)
Chọn B.
Phần II. Tự luận (7 điểm):
Bài 1
Phương pháp:
a) Đổi số thập phân sang phân số
Thực hiện các phép toán với số hữu tỉ.
b) Lũy thừa của một số hữu tỉ: \({\left( {\dfrac{a}{b}} \right)^n} = \dfrac{{{a^n}}}{{{b^n}}}\,\,\left( {b \ne 0;n \in \mathbb{Z}} \right)\)
Thực hiện các phép toán với số hữu tỉ.
c) Tính căn bậc hai số học của một số thực
Thực hiện các phép toán với số hữu tỉ.
d) Lũy thừa của một số hữu tỉ: \({\left( {\dfrac{a}{b}} \right)^n} = \dfrac{{{a^n}}}{{{b^n}}}\,\,\left( {b \ne 0;n \in \mathbb{Z}} \right)\)
Tính căn bậc hai số học của một số thực
Vận dụng kiến thức giá trị tuyệt đối của một số thực: \(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,\,\,\,khi\,\,\,x > 0\\ - x\,\,\,khi\,\,x < 0\\0\,\,\,\,\,\,\,khi\,\,\,x = 0\end{array} \right.\)
Thực hiện các phép toán với số hữu tỉ.
Cách giải:
a) \(\dfrac{2}{9} + \dfrac{1}{3}:\left( { - \dfrac{3}{2}} \right) + \dfrac{1}{2}.{\left( { - 0,5} \right)^0}\)
\(\begin{array}{l} = \dfrac{2}{9} + \dfrac{1}{3}.\left( {\dfrac{{ - 2}}{3}} \right) + \dfrac{1}{2}.1\\ = \dfrac{2}{9} + \dfrac{{ - 2}}{9} + \dfrac{1}{2}\\ = 0 + \dfrac{1}{2}\\ = \dfrac{1}{2}\end{array}\)
b) \({\left( {\dfrac{{ - 1}}{2}} \right)^2} - \dfrac{5}{8}:{\left( {0,5} \right)^3} - \dfrac{5}{3}.\left( { - 6} \right)\)
\(\begin{array}{l} = \dfrac{{{{\left( { - 1} \right)}^2}}}{{{2^2}}} - \dfrac{5}{8}:{\left( {\dfrac{1}{2}} \right)^3} - 5.\left( { - 2} \right)\\ = \dfrac{1}{4} - \dfrac{5}{8}:\dfrac{{{1^3}}}{{{2^3}}} - \left( { - 10} \right)\\ = \dfrac{1}{4} - \dfrac{5}{8}:\dfrac{1}{8} + 10\\ = \dfrac{1}{4} - \dfrac{5}{8}.\dfrac{8}{1} + 10\\ = \dfrac{1}{4} - 5 + 10 = \dfrac{1}{4} + 5\\ = \dfrac{1}{4} + \dfrac{{20}}{4} = \dfrac{{21}}{4}\end{array}\)
c) \(\sqrt {0,04} + \sqrt {0,25} + 2,31\)
\(\begin{array}{l} = \sqrt {{{\left( {0,2} \right)}^2}} + \sqrt {{{\left( {0,5} \right)}^2}} + 2,31\\ = 0,2 + 0,5 + 2,31\\ = 3,01\end{array}\)
d) \(\left| {\sqrt {169} - \sqrt {900} } \right| - \left| {\dfrac{{ - 5}}{4}} \right|:{\left( {\dfrac{1}{3} - \dfrac{1}{2}} \right)^2}\)
\(\begin{array}{l} = \left| {\sqrt {{{13}^2}} - \sqrt {{{30}^2}} } \right| - \dfrac{5}{4}:{\left( {\dfrac{2}{6} - \dfrac{3}{6}} \right)^2}\\ = \left| {13 - 30} \right| - \dfrac{5}{4}:{\left( {\dfrac{1}{6}} \right)^2}\\ = \left| { - 17} \right| - \dfrac{5}{4}:\dfrac{1}{{36}}\\ = 17 - \dfrac{5}{4}.36\\ = 17 - 45\\ = - 28\end{array}\)
Bài 2
Phương pháp:
a) Thực hiện các phép toán với số hữu tỉ
Vận dụng quy tắc chuyển vế, tìm \(x\).
b) Giải \({\left[ {A\left( x \right)} \right]^2} = {a^2} = {\left( { - a} \right)^2}\)
Trường hợp 1: \(A\left( x \right) = a\)
Trường hợp 2: \(A\left( x \right) = - a\)
c) Tính căn bậc hai số học của số thực
Thực hiện các phép toán với số hữu tỉ
Vận dụng quy tắc chuyển vế, tìm \(x\).
d) \(\left| x \right| = a\)
Trường hợp \(a < 0\), khi đó phương trình không có nghiệm \(x\)
Trường hợp \(a > 0\), vận dụng kiến thức giá trị tuyệt đối của một số thực: \(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,\,\,\,khi\,\,\,x > 0\\ - x\,\,\,khi\,\,x < 0\\0\,\,\,\,\,\,\,khi\,\,\,x = 0\end{array} \right.\)
Cách giải:
a) \(\dfrac{1}{3}x + \dfrac{2}{5}\left( {x - 1} \right) = 0\)
\(\begin{array}{l}\dfrac{1}{3}x + \dfrac{2}{5}x - \dfrac{2}{5} = 0\\x.\left( {\dfrac{1}{3} + \dfrac{2}{5}} \right) = \dfrac{2}{5}\\x.\left( {\dfrac{5}{{15}} + \dfrac{6}{{15}}} \right) = \dfrac{2}{5}\\x.\dfrac{{11}}{{15}} = \dfrac{2}{5}\\x = \dfrac{2}{5}:\dfrac{{11}}{{15}}\\x = \dfrac{2}{5}.\dfrac{{15}}{{11}}\\x = \dfrac{6}{{11}}\end{array}\)
Vậy \(x = \dfrac{6}{{11}}\)
b) \({\left( {2x + 1} \right)^2} = \dfrac{{36}}{{25}}\)
\({\left( {2x + 1} \right)^2} = {\left( {\dfrac{6}{5}} \right)^2} = {\left( { - \dfrac{6}{5}} \right)^2}\)
Trường hợp 1:
\(\begin{array}{l}2x + 1 = \dfrac{6}{5}\\2x = \dfrac{6}{5} - 1 = \dfrac{6}{5} - \dfrac{5}{5}\\2x = \dfrac{1}{5}\\x = \dfrac{1}{5}:2 = \dfrac{1}{5}.\dfrac{1}{2}\\x = \dfrac{1}{{10}}\end{array}\)
Vậy \(x \in \left\{ {\dfrac{1}{{10}};\dfrac{{ - 11}}{{10}}} \right\}\)
Trường hợp 2:
\(\begin{array}{l}2x + 1 = - \dfrac{6}{5}\\2x = \dfrac{{ - 6}}{5} - 1 = \dfrac{{ - 6}}{5} - \dfrac{5}{5}\\2x = \dfrac{{ - 11}}{5}\\x = \dfrac{{ - 11}}{5}:2 = \dfrac{{ - 11}}{5}.\dfrac{1}{2}\\x = \dfrac{{ - 11}}{{10}}\end{array}\)
c) \(\dfrac{1}{2}x + \sqrt {0,04} = \sqrt {1,96} \)
\(\begin{array}{l}\dfrac{1}{2}x + \sqrt {{{\left( {0,2} \right)}^2}} = \sqrt {{{\left( {1,4} \right)}^2}} \\\dfrac{1}{2}x + 0,2 = 1,4\\\dfrac{1}{2}x = 1,4 - 0,2 = 1,2\\x = 1,2:\dfrac{1}{2} = 1,2.2\\x = 2,4\end{array}\)
Vậy \(x = 2,4\).
d) \(\left| {\left| {2x - 1} \right| + \dfrac{1}{2}} \right| = \dfrac{4}{5}\)
Trường hợp 1:
\(\begin{array}{l}\left| {2x - 1} \right| + \dfrac{1}{2} = \dfrac{4}{5}\\\left| {2x - 1} \right| = \dfrac{4}{5} - \dfrac{1}{2} = \dfrac{8}{{10}} - \dfrac{5}{{10}}\\\left| {2x - 1} \right| = \dfrac{3}{{10}}\end{array}\)
*\(2x - 1 = \dfrac{3}{{10}}\)
\(\begin{array}{l}2x = \dfrac{3}{{10}} + 1 = \dfrac{3}{{10}} + \dfrac{{10}}{{10}}\\2x = \dfrac{{13}}{{10}}\\x = \dfrac{{13}}{{10}}:2 = \dfrac{{13}}{{10}}.\dfrac{1}{2}\\x = \dfrac{{13}}{{20}}\end{array}\)
*\(2x - 1 = \dfrac{{ - 3}}{{10}}\)
\(\begin{array}{l}2x = \dfrac{{ - 3}}{{10}} + 1 = \dfrac{{ - 3}}{{10}} + \dfrac{{10}}{{10}}\\2x = \dfrac{7}{{10}}\\x = \dfrac{7}{{10}}:2 = \dfrac{7}{{10}}.\dfrac{1}{2}\\x = \dfrac{7}{{20}}\end{array}\)
Trường hợp 2:
\(\begin{array}{l}\left| {2x - 1} \right| + \dfrac{1}{2} = - \dfrac{4}{5}\\\left| {2x - 1} \right| = - \dfrac{4}{5} - \dfrac{1}{2} = \dfrac{{ - 8}}{{10}} - \dfrac{5}{{10}}\\\left| {2x - 1} \right| = \dfrac{{ - 13}}{{10}}\end{array}\)
Vì \(\dfrac{{ - 13}}{{10}} < 0\) nên không có \(x\) thỏa mãn \(\left| {2x - 1} \right| = \dfrac{{ - 13}}{{10}}\).
Vậy \(x \in \left\{ {\dfrac{{13}}{{20}};\dfrac{7}{{20}}} \right\}\)
Bài 3
Phương pháp:
Áp dụng tính chất hai đường thẳng song song, tiên đề Ơ-Clit.
Tính chất: Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau.
Cách giải:
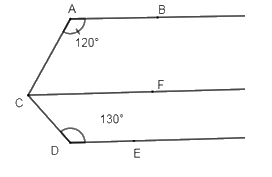
Kẻ \(CF//\,AB \Rightarrow \widehat {BAC} + \widehat {ACF} = {180^0}\) (2 góc trong cùng phía)
\( \Rightarrow \widehat {ACF} = {180^0} - \widehat {BAC} = {180^0} - {120^0} = {60^0}\)
Ta có: \(\left\{ \begin{array}{l}AB//\,DE\\CF//\,AB\end{array} \right.\left( {gt} \right) \Rightarrow DE//\,CF.\)
\( \Rightarrow \widehat {FCD} + \widehat {C{\rm{D}}E} = {180^0}\) (2 góc trong cùng phía)
\(\begin{array}{l} \Rightarrow \widehat {DCF} = {180^0} - \widehat {C{\rm{D}}E} = {180^0} - {130^0} = {50^0}\\ \Rightarrow \widehat {AC{\rm{D}}} = \widehat {ACF} + \widehat {FC{\rm{D}}} = {60^0} + {50^0} = {110^0}\\ \Rightarrow \widehat {BAC} + \widehat {AC{\rm{D}}} + \widehat {C{\rm{D}}E} = {120^0} + {110^0} + {130^0} = {360^0}\end{array}\)
Bài 4
Phương pháp:
a) Thể tích của hình lăng trụ đứng tam giác: \(V = S\)đáy\(.h\)
Trong đó: \(V:\) thể tích của hình lăng trụ đứng tam giác
\(S\)đáy: diện tích một đáy của hình lăng trụ đứng tam giác
\(h\): chiều cao của hình lăng trụ đứng tam giác
b) Diện tích xung quanh của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác: \({S_{xq}} = C\)đáy.\(h\)
Trong đó: \({S_{xq}}:\) diện tích xung quanh hình lăng trụ đứng tam giác
\(C\)đáy: diện tích một đáy của hình lăng trụ đứng tam giác
\(h\): chiều cao của hình lăng trụ đứng tam giác
Chi phí làm hộp = (diện tích xung quanh + diện tích hai đáy) . giá tiền 1 mét vuông bìa
Cách giải:
a) Đáy của hình lăng trụ tam giác là một tam giác vuông nên diện tích đáy là: \(S\)đáy\( = \)\(\dfrac{1}{2}.9.12 = 54\,\left( {c{m^2}} \right)\)
Thể tích cái bánh là: \(V = S\)đáy\(.h = 54.5 = 270\,\left( {c{m^3}} \right)\)
b) Chu vi đáy của cái bánh là: \(C = 9 + 12 + 15 = 36\,\left( {cm} \right)\)
Diện tích xung quanh của cái bánh là: \({S_{xq}} = C.h = 36.5 = 180\,\left( {c{m^2}} \right)\)
Diện tích hai đáy của cái bánh là: \(S = 2.54 = 108\,\left( {c{m^2}} \right)\)
Diện tích làm hộp của cái bánh là: \({S_{xq}} + S = 180 + 108 = 288\left( {c{m^2}} \right) = 0,0288\,\left( {{m^2}} \right)\)
Chi phí làm hộp là: \(0,0288.22500 = 648\) (đồng)
Bài 5
Phương pháp:
Đánh giá các số hạng của tổng để tìm giá trị nhỏ nhất của \(A\).
Chú ý: \({x^2} \ge 0,\forall x \in \mathbb{R}\).
Cách giải:
Ta có: \({x^2} \ge 0;\sqrt x \ge 0\) với mọi số thực \(x \ge 0\) nên \({x^2} + \sqrt x \ge 0\) với mọi số thực \(x \ge 0\).
Suy ra \({x^2} + \sqrt x - 113 \ge - 113\) với mọi số thực \(x \ge 0.\) Hay \(A \ge - 113\) với mọi số thực \(x \ge 0.\)
Dấu “=” xảy ra \( \Leftrightarrow x = 0\).
Vậy \(\min A = - 113 \Leftrightarrow x = 0\).
8.D | 10.B |
Đề thi học kì 1 Toán 7 - Đề số 10, chương trình Chân trời sáng tạo, là một bài kiểm tra quan trọng giúp học sinh đánh giá mức độ nắm vững kiến thức đã học trong nửa học kì đầu tiên. Đề thi bao gồm các dạng bài tập khác nhau, từ trắc nghiệm đến tự luận, tập trung vào các chủ đề chính như số hữu tỉ, số thực, biểu thức đại số, phương trình bậc nhất một ẩn, và các ứng dụng thực tế của toán học.
Đề thi thường được chia thành các phần sau:
Phần này tập trung vào việc ôn tập các khái niệm về số hữu tỉ, số thực, cách biểu diễn trên trục số, và các phép toán trên chúng. Học sinh cần nắm vững các tính chất của phép cộng, trừ, nhân, chia số hữu tỉ và số thực, cũng như cách so sánh và sắp xếp chúng.
Học sinh cần hiểu rõ về các khái niệm như biến, hằng số, biểu thức đại số, và cách đơn giản hóa biểu thức. Các bài tập thường yêu cầu học sinh thực hiện các phép toán cộng, trừ, nhân, chia đa thức, và sử dụng các quy tắc về dấu ngoặc.
Đây là một trong những chủ đề quan trọng nhất của chương trình Toán 7. Học sinh cần nắm vững các khái niệm về phương trình, nghiệm của phương trình, và các bước giải phương trình bậc nhất một ẩn. Các bài tập thường yêu cầu học sinh giải phương trình, tìm nghiệm, và kiểm tra lại nghiệm.
Phần này giúp học sinh hiểu rõ hơn về tính ứng dụng của toán học trong cuộc sống. Các bài tập thường liên quan đến các tình huống thực tế như tính tiền, đo đạc, và giải quyết các vấn đề liên quan đến số lượng và tỷ lệ.
Để giải đề thi hiệu quả, học sinh cần:
Giaitoan.edu.vn cung cấp nhiều tài nguyên hỗ trợ học tập, bao gồm:
Để đạt kết quả tốt trong kỳ thi học kì 1, học sinh cần:
Đề thi học kì 1 Toán 7 - Đề số 10 - Chân trời sáng tạo là một cơ hội tốt để học sinh đánh giá kiến thức và chuẩn bị cho các kỳ thi tiếp theo. Với sự chuẩn bị kỹ lưỡng và tinh thần học tập tích cực, các em sẽ đạt được kết quả tốt nhất.