Giaitoan.edu.vn xin giới thiệu Đề thi học kì 1 Toán 7 Chân trời sáng tạo - Đề số 14, một công cụ hữu ích giúp học sinh ôn luyện và đánh giá năng lực trước kỳ thi quan trọng. Đề thi được biên soạn bám sát chương trình học, đảm bảo tính chính xác và cập nhật.
Với cấu trúc đề thi đa dạng, bao gồm các dạng bài tập khác nhau, học sinh có thể rèn luyện kỹ năng giải quyết vấn đề và áp dụng kiến thức đã học vào thực tế.
Điểm A trong hình dưới đây biểu diễn số hữu tỉ nào?
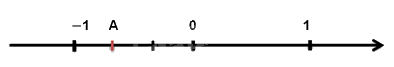
Cho các số \(\frac{2}{{ - 5}};\,\frac{{ - 3}}{{ - 4}} ;\,\frac{5}{7};\,\sqrt 2 ;\,\frac{{ - 9}}{{11}}\). Các số hữu tỉ dương là:
Cho biểu thức \({\left( {\frac{{ - 2}}{3}} \right)^6}:{\left( {\frac{4}{9}} \right)^2}\). Kết quả phép tính ở dạng lũy thừa là:
Cho 2 số thực a và b với \(a > 0\) và \(b < 0\). Giá trị tuyệt đối của tích a.b là:
Khi thực hiện phép tính \(\sqrt {{3^2} + {4^2}} \). Biến đổi đúng là:
Cho các số: \(\frac{2}{3};\,\frac{{ - 3}}{5};\,\frac{7}{{20}};\,\frac{5}{{22}};\,\frac{1}{{ - 8}};\,\frac{\pi }{2}\). Các số viết được dưới dạng số thập phân hữu hạn là:
Làm tròn số 75647 với độ chính xác \(d = 50\). Kết quả là:
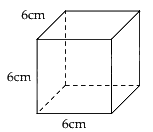
Cho hình lập phương như hình vẽ dưới đây. Diện tích xung quanh của hình lập phương là:
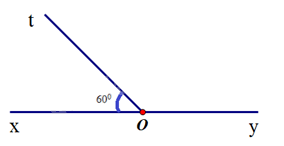
Cho hai góc \(\widehat {xOt}\) và \(\widehat {tOy}\) là hai góc kề bù. Biết \(\widehat {xOt} = {60^0}\), số đo góc \(\widehat {tOy}\) là:
Nếu một đường thẳng cắt hai đường thẳng song song, khẳng định đúng là:
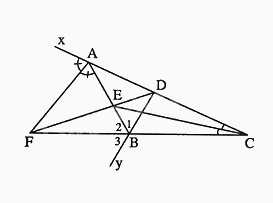
Cho hình vẽ dưới đây, khẳng định đúng là:
Cho hai đường thẳng m và n song song với nhau như hình vẽ dưới đây, giá trị của x là:
Thực hiện phép tính:
a) \(\frac{{ - 7}}{5}.\left( {\frac{{15}}{{14}} + \frac{5}{7}} \right) + \left| {\frac{{ - 7}}{2}} \right|\).
b) \(\frac{1}{{13}} + \left( {\frac{{ - 5}}{{18}} - \frac{1}{{13}} + \frac{9}{{25}}} \right) - \left[ {{{\left( {\frac{3}{5}} \right)}^2} - \frac{{\sqrt {25} }}{{18}} + \frac{{19}}{{11}}} \right]\).
Ông Newton gửi tiết kiệm 500 triệu đồng vào một ngân hàng theo thể thức kì hạn một năm. Hết thời hạn một năm, ông nhận được cả vốn lần lãi là 534 triệu đồng. Tính lãi suất ngân hàng theo thể thức gửi tiết kiệm này.
Bảng sau thống kê điểm thi môn Toán của lớp 7A:

Tính điểm thi trung bình môn Toán của lớp 7A?
Cho hình vẽ sau:
a) Chứng minh: \(m//n\).
b) Tính số đo góc \({\widehat K_1}\).
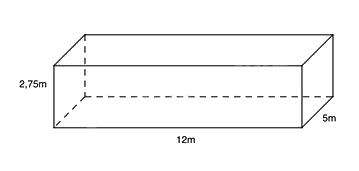
Một bể bơi dạng hình hộp chữ nhật có chiều dài 12m, chiều rộng 5m và sâu 2,75m như hình vẽ.
a) Tính diện tích xung quanh thành bể và diện tích đáy của bể bơi.
b) Hỏi người thợ phải dùng bao nhiêu viên gạch men để lát đáy và xung quanh thành bể đó? Biết rằng mỗi viên gạch có chiều dài 25cm, chiều rộng 20 cm và diện tích mạch vữa lát không đáng kể.
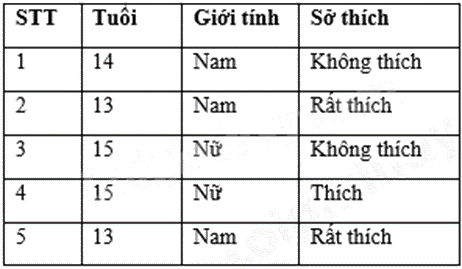
Tìm hiểu về sở thích đối với môn bơi lội của 5 bạn học sinh một trường Trung học cơ sở được cho bởi bảng thống kê sau:
Hãy phân loại dữ liệu trong bảng thống kê theo hai tiêu chí định tính và định lượng. Tính độ tuổi trung bình của các bạn được điều tra.
Điểm A trong hình dưới đây biểu diễn số hữu tỉ nào?
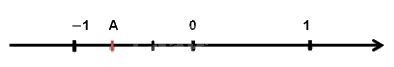
Đáp án : C
Dựa vào cách biểu diễn số hữu tỉ trên trục số.
Điểm A nằm bên trái số 0 nên A là số hữu tỉ âm. Ta thấy từ -1 đến 0 được chia làm 3 phần bằng nhau nên mẫu số bằng 3.
Điểm A chiếm hai phần về phía chiều âm trục số nên tử số bằng -2.
Vậy số hữu tỉ A = \( - \frac{2}{3}\)
Cho các số \(\frac{2}{{ - 5}};\,\frac{{ - 3}}{{ - 4}} ;\,\frac{5}{7};\,\sqrt 2 ;\,\frac{{ - 9}}{{11}}\). Các số hữu tỉ dương là:
Đáp án : D
Số hữu tỉ dương là số lớn hơn 0.
Ta có:
\(\begin{array}{l}\frac{2}{{ - 5}} = \frac{{ - 2}}{5} < 0\\\frac{{ - 3}}{{ - 4}} = \frac{3}{4} > 0\\\frac{5}{7} > 0\end{array}\)
\(\sqrt 2 \) không phải là số hữu tỉ.
\(\frac{{ - 9}}{{11}} < 0\)
Vậy chỉ có \(\frac{{ - 3}}{{ - 4}};\frac{5}{7}\) là số hữu tỉ dương.
Cho biểu thức \({\left( {\frac{{ - 2}}{3}} \right)^6}:{\left( {\frac{4}{9}} \right)^2}\). Kết quả phép tính ở dạng lũy thừa là:
Đáp án : A
Biến đổi biểu thức về phép chia hai lũy thừa cùng cơ số.
Ta có:
\({\left( {\frac{{ - 2}}{3}} \right)^6}:{\left( {\frac{4}{9}} \right)^2} = {\left( {\frac{{ - 2}}{3}} \right)^6}:{\left[ {{{\left( {\frac{{ - 2}}{3}} \right)}^2}} \right]^2} = {\left( {\frac{{ - 2}}{3}} \right)^6}:{\left( {\frac{{ - 2}}{3}} \right)^4} = {\left( {\frac{{ - 2}}{3}} \right)^{6 - 4}} = {\left( {\frac{{ - 2}}{3}} \right)^2} = {\left( {\frac{2}{3}} \right)^2}\).
Cho 2 số thực a và b với \(a > 0\) và \(b < 0\). Giá trị tuyệt đối của tích a.b là:
Đáp án : B
Sử dụng định nghĩa giá trị tuyệt đối của một số:
\(\left| x \right| = \left\{ \begin{array}{l}x\,khi\,x \ge 0\\ - x\,khi\,x < 0\end{array} \right.\).
Vì a > 0 và b < 0 nên tích a.b < 0.
Khi đó giá trị tuyệt đối của tích a.b là: \(\left| {ab} \right| = - \left( {ab} \right) = - ab\).
Khi thực hiện phép tính \(\sqrt {{3^2} + {4^2}} \). Biến đổi đúng là:
Đáp án : A
Tính phép tính trong căn bậc hai.
Ta có: \(\sqrt {{3^2} + {4^2}} = \sqrt {9 + 16} = \sqrt {25} \).
Cho các số: \(\frac{2}{3};\,\frac{{ - 3}}{5};\,\frac{7}{{20}};\,\frac{5}{{22}};\,\frac{1}{{ - 8}};\,\frac{\pi }{2}\). Các số viết được dưới dạng số thập phân hữu hạn là:
Đáp án : C
Các phân số tối giản với mẫu số dương mà mẫu chỉ có ước nguyên tố là 2 và 5 đều viết được dưới dạng số thập phân hữu hạn.
Trong các số hữu tỉ trên, chỉ có \(\frac{{ - 3}}{5};\frac{7}{{20}};\frac{1}{{ - 8}}\) có mẫu số chỉ có ước nguyên tố là 2 và 5 nên các số này là số thập phân hữu hạn.
Đặc biệt, số \(\frac{\pi }{2}\) có mẫu số bằng 2 nhưng tử số là số thập phân vô hạn không tuần hoàn nên \(\frac{\pi }{2}\) không phải là số thập phân hữu hạn.
Làm tròn số 75647 với độ chính xác \(d = 50\). Kết quả là:
Đáp án : C
Dựa vào cách làm tròn số với độ chính xác cho trước.
Làm tròn số 75647 với độ chính xác 50 tức là làm tròn số 75647 đến hàng trăm.
Số 75647 đến hàng trăm làm tròn đến hàng trăm ta được số 75 600.
Cho hình lập phương như hình vẽ dưới đây. Diện tích xung quanh của hình lập phương là:
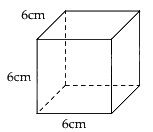
Đáp án : B
Dựa vào công thức tính diện tích xung quanh của hình lập phương. Sxq = 4.cạnh2.
Diện tích xung quanh hình lập phương đó là: 4.62 = 144 (cm2).
Cho hai góc \(\widehat {xOt}\) và \(\widehat {tOy}\) là hai góc kề bù. Biết \(\widehat {xOt} = {60^0}\), số đo góc \(\widehat {tOy}\) là:
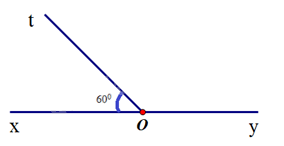
Đáp án : D
Hai góc kề bù có tổng số đo bằng 1800.
Ta có góc xOt và góc tOy là hai góc kề bù nên \(\widehat {xOt} + \widehat {tOy} = {180^0}\). Suy ra \(\widehat {tOy} = {180^0} - {60^0} = {120^0}\).
Nếu một đường thẳng cắt hai đường thẳng song song, khẳng định đúng là:
Đáp án : A
Dựa vào tính chất hai đường thẳng song song.
Nếu một đường thẳng cắt hai đường thẳng song song thì:
+ Hai góc so le trong bằng nhau
+ Hai góc đồng vị bằng nhau
+ Các góc so le ngoài bằng nhau
+ Các góc trong cùng phía bù nhau
nên A đúng.
Cho hình vẽ dưới đây, khẳng định đúng là:
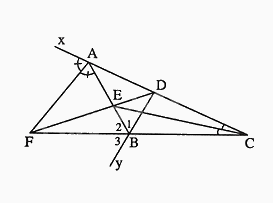
Đáp án : B
Dựa vào dấu hiệu nhận biết tia phân giác
Ta có tia AF nằm AB và Ax, \(\widehat {BAF} = \widehat {FAx}\) nên AF là tia phân giác của góc BAx.
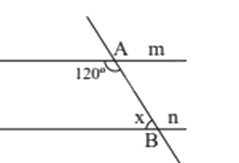
Cho hai đường thẳng m và n song song với nhau như hình vẽ dưới đây, giá trị của x là:
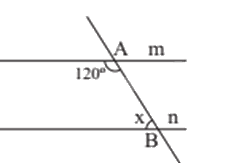
Đáp án : D
Dựa vào tính chất hai góc kề bù và hai góc so le trong của hai đường thẳng song song.
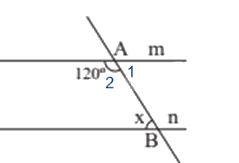
Ta có góc A1 và góc A2 là hai góc kề bù nên số đo góc A1 là: \({180^0} - \widehat {{A_2}} = {180^0} - {120^0} = {60^0}\).
Vì m // n nên \(\widehat {{A_1}} = x = {60^0}\) (hai góc so le trong)
Thực hiện phép tính:
a) \(\frac{{ - 7}}{5}.\left( {\frac{{15}}{{14}} + \frac{5}{7}} \right) + \left| {\frac{{ - 7}}{2}} \right|\).
b) \(\frac{1}{{13}} + \left( {\frac{{ - 5}}{{18}} - \frac{1}{{13}} + \frac{9}{{25}}} \right) - \left[ {{{\left( {\frac{3}{5}} \right)}^2} - \frac{{\sqrt {25} }}{{18}} + \frac{{19}}{{11}}} \right]\).
- Sử dụng tính chất của phép nhân.
- Sử dụng định nghĩa giá trị tuyệt đối của một số:
\(\left| x \right| = \left\{ \begin{array}{l}x\,khi\,x \ge 0\\ - x\,khi\,x < 0\end{array} \right.\).
a) \(\frac{{ - 7}}{5}.\left( {\frac{{15}}{{14}} + \frac{5}{7}} \right) + \left| {\frac{{ - 7}}{2}} \right|\)
\(\begin{array}{l} = \frac{{ - 7}}{5}.\frac{{15}}{{14}} + \left( {\frac{{ - 7}}{5}} \right).\frac{5}{7} + \frac{7}{2}\\ = \frac{{ - 3}}{2} + \left( { - 1} \right) + \frac{7}{2} = \left( {\frac{{ - 3}}{2} + \frac{7}{2}} \right) - 1 = 2 - 1 = 1\end{array}\)
b) \(\frac{1}{{13}} + \left( {\frac{{ - 5}}{{18}} - \frac{1}{{13}} + \frac{9}{{25}}} \right) - \left[ {{{\left( {\frac{3}{5}} \right)}^2} - \frac{{\sqrt {25} }}{{18}} + \frac{{19}}{{11}}} \right]\)
\(\begin{array}{l} = \frac{1}{{13}} + \left( {\frac{{ - 5}}{{18}} - \frac{1}{{13}} + \frac{9}{{25}}} \right) - \left[ {\frac{9}{{25}} - \frac{5}{{18}} + \frac{{19}}{{11}}} \right]\\ = \frac{1}{{13}} - \frac{5}{{18}} - \frac{1}{{13}} + \frac{9}{{25}} - \frac{9}{{25}} + \frac{5}{{18}} + \frac{{19}}{{11}}\\ = \left( {\frac{1}{{13}} - \frac{1}{{13}}} \right) + \left( {\frac{5}{{18}} - \frac{5}{{18}}} \right) + \left( {\frac{9}{{25}} - \frac{9}{{25}}} \right) + \frac{{19}}{{11}}\\ = \frac{{19}}{{11}}\end{array}\)
Ông Newton gửi tiết kiệm 500 triệu đồng vào một ngân hàng theo thể thức kì hạn một năm. Hết thời hạn một năm, ông nhận được cả vốn lần lãi là 534 triệu đồng. Tính lãi suất ngân hàng theo thể thức gửi tiết kiệm này.
Tính số tiền lãi ông Newton nhận được khi hết thời hạn một năm.
Tính lãi suất ngân hàng.
Số tiền lãi ông Newton nhận được khi hết thời hạn một năm là:
\(534 - 500 = 34\)(triệu đồng)
Lãi suất ngân hàng là:
\(\frac{{34}}{{500}}.100\% = 6,8\% \)
Bảng sau thống kê điểm thi môn Toán của lớp 7A:

Tính điểm thi trung bình môn Toán của lớp 7A?
Tính tổng số điểm của lớp 7A.
Tính tổng số học sinh lớp 7A.
Điểm thi trung bình của lớp 7A bằng tổng số điểm chia cho tổng số học sinh.
Tổng điểm lớp 7A:
\(S = 4.1 + 5.2 + 6.5 + 7.6 + 8.7 + 9.10 + 10.4 = 272\)
Số học sinh lớp 7A:
\(N = 1 + 2 + 5 + 6 + 7 + 10 + 4 = 35\)
Điểm trung bình môn Toán của lớp 7A là:
\(\overline X = \frac{S}{N} = \frac{{272}}{{35}} \approx 7,8\)
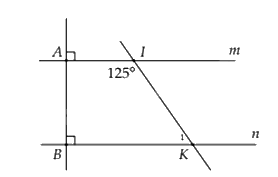
Cho hình vẽ sau:
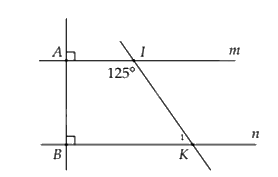
a) Chứng minh: \(m//n\).
b) Tính số đo góc \({\widehat K_1}\).
a) Sử dụng dấu hiệu nhận biết hai đường thẳng song song.
b) Dựa vào tính chất của đường thẳng song song và hai góc kề bù.
a) Ta có:
\(\left. \begin{array}{l}m \bot AB\\n \bot AB\end{array} \right\} \Rightarrow m//n\)
b) Ta có:
\(m//n \Rightarrow \widehat {IKn} = \widehat {AIK} = {125^0}(soletrong)\)
Mà: \(\widehat {IKn} + \widehat {{K_1}} = {180^0}\)(kề bù)
\( \Rightarrow {125^0} + {\widehat K_1} = {180^0} \Rightarrow {\widehat K_1} = {55^0}\)
Một bể bơi dạng hình hộp chữ nhật có chiều dài 12m, chiều rộng 5m và sâu 2,75m như hình vẽ.
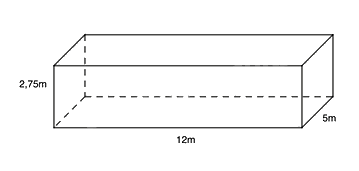
a) Tính diện tích xung quanh thành bể và diện tích đáy của bể bơi.
b) Hỏi người thợ phải dùng bao nhiêu viên gạch men để lát đáy và xung quanh thành bể đó? Biết rằng mỗi viên gạch có chiều dài 25cm, chiều rộng 20 cm và diện tích mạch vữa lát không đáng kể.
a) Sử dụng công thức tính diện tích xung quanh hình hộp chữ nhật: Sxq = chu vi đáy.chiều cao.
Sử dụng công thức tính diện tích hình chữ nhật để tính diện tích đáy bể bơi.
b) Tổng diện tích xung quanh và diện tích đáy bể chính là diện tích cần lát gạch.
Tính diện tích mỗi viên gạch.
Số viên gạch bằng diện tích cần lát : diện tích mỗi viên gạch.
a) Diện tích xung quanh thành bể:
\(\left[ {(12 + 5).2} \right].2,75 = 93,5\,{m^2}\)
Diện tích đáy bể:
\(12.5 = 60\,{m^2}\)
b) Diện tích cần lát gạch:
\(93,5 + 60 = 153,5\,{m^2}\)
Diện tích mỗi viên gạch:
\(0,25.0,2 = 0,05\,{m^2}\)
Số viên gạch cần lát là: \(153,5:0,05 = 3070\)(viên).
Vậy cần dùng 3070 viên gạch để lát.
Tìm hiểu về sở thích đối với môn bơi lội của 5 bạn học sinh một trường Trung học cơ sở được cho bởi bảng thống kê sau:
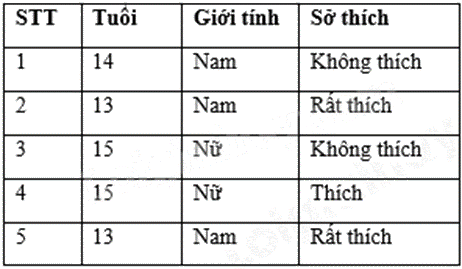
Hãy phân loại dữ liệu trong bảng thống kê theo hai tiêu chí định tính và định lượng. Tính độ tuổi trung bình của các bạn được điều tra.
Dữ liệu định tính là dữ liệu không phải là số.
Dữ liệu định lượng là dữ liệu số.
Độ tuổi trung bình bằng tổng số tuổi chia cho số lượng người.
- Dữ liệu định tính: Giới tính, sở thích.
- Dữ liệu định lượng: Tuổi.
- Độ tuổi trung bình: \(\frac{{14 + 13.2 + 15.2}}{5} = 14\) tuổi
Kỳ thi học kì 1 Toán 7 đóng vai trò quan trọng trong việc đánh giá quá trình học tập của học sinh trong nửa học kỳ đầu tiên. Đề thi không chỉ kiểm tra kiến thức mà còn đánh giá khả năng vận dụng kiến thức vào giải quyết các bài toán thực tế. Đề thi học kì 1 Toán 7 Chân trời sáng tạo - Đề số 14 được thiết kế để đáp ứng những yêu cầu đó.
Đề thi học kì 1 Toán 7 Chân trời sáng tạo - Đề số 14 thường bao gồm các phần sau:
Các dạng bài tập thường xuất hiện trong đề thi bao gồm:
Ví dụ: Tính giá trị của biểu thức A = (1/2 + 1/3) * 6/5. Hướng dẫn: Thực hiện các phép tính trong ngoặc trước, sau đó thực hiện phép nhân.
Ví dụ: Giải phương trình 2x + 3 = 7. Hướng dẫn: Chuyển số hạng tự do sang vế phải, sau đó chia cả hai vế cho hệ số của x.
Ví dụ: Cho hai đường thẳng a và b cắt đường thẳng c. Biết góc so le trong bằng nhau. Chứng minh a song song b. Hướng dẫn: Áp dụng định lý về hai đường thẳng song song.
Luyện tập thường xuyên là yếu tố then chốt để đạt kết quả tốt trong kỳ thi học kì. Học sinh nên giải nhiều đề thi khác nhau để làm quen với các dạng bài tập và rèn luyện kỹ năng giải quyết vấn đề. Giaitoan.edu.vn cung cấp một kho đề thi phong phú, đa dạng, giúp học sinh có thể luyện tập hiệu quả.
Giaitoan.edu.vn là một nền tảng học toán online uy tín, cung cấp các tài liệu học tập chất lượng, bao gồm:
Hãy truy cập giaitoan.edu.vn ngay hôm nay để bắt đầu hành trình chinh phục môn Toán!
Chương trình Toán 7 Chân trời sáng tạo tập trung vào việc phát triển tư duy logic, khả năng giải quyết vấn đề và ứng dụng toán học vào thực tế. Chương trình cũng chú trọng đến việc rèn luyện các kỹ năng tính toán, vẽ hình và chứng minh. Việc nắm vững kiến thức và kỹ năng trong chương trình Toán 7 là nền tảng quan trọng cho việc học tập các môn Toán ở các lớp trên.
Hãy dành thời gian ôn tập kiến thức đều đặn, làm bài tập thường xuyên và tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè khi gặp khó khăn. Đừng ngại đặt câu hỏi và trao đổi kiến thức với những người xung quanh. Chúc các em học sinh đạt kết quả tốt trong kỳ thi học kì 1!