Chào mừng các em học sinh đến với đề thi giữa kì 1 Toán 7 - Đề số 8 chương trình Kết nối tri thức. Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong giai đoạn đầu của năm học.
Giaitoan.edu.vn cung cấp đề thi kèm đáp án chi tiết, giúp các em tự học và kiểm tra kết quả một cách hiệu quả. Chúc các em làm bài tốt!
Phần trắc nghiệm (3 điểm) Câu 1. Chọn khẳng định đúng
Phần trắc nghiệm (3 điểm)
Câu 1. Chọn khẳng định đúng
A. \(\frac{3}{2} \in \mathbb{Q}.\)
B. \(\frac{3}{2} \in \mathbb{Z}\).
C. \(\frac{{ - 9}}{5} \notin \mathbb{Q}\).
D. \( - 6 \in \mathbb{N}\).
Câu 2. Số hữu tỉ dương là
A. \(\frac{{ - 11}}{3}.\)
B. \( - \frac{{12}}{5}.\)
C. \(\frac{{ - 5}}{{ - 7}}.\)
D. \(\frac{{15}}{{ - 13}}.\)
Câu 3. Kết quả phép tính \(\frac{3}{7} + \frac{4}{7}.\frac{{ - 21}}{{35}}\) là
A. \(\frac{3}{{35}}\).
B. \(\frac{{ - 21}}{{35}}\).
C. \(\frac{{ - 11}}{{35}}\).
D. \(\frac{{11}}{{35}}\).
Câu 4. Giá trị của \(x\) trong phép tính \(\frac{2}{5} - x = \frac{1}{3}\) bằng
A. \(\frac{7}{{30}}.\)
B. \(\frac{{ - 1}}{{15}}.\)
C. \(\frac{{11}}{{15}}.\)
D. \(\frac{1}{{15}}.\)
Câu 5. Căn bậc hai số học của 81 là
A. 9 và -9
B. \(\frac{{ - 1}}{{81}}.\)
C. \( - 9.\)
D. \(9.\)
Câu 6. Khẳng định đúng là
A. \(\left| { - 3,5} \right| = - 3,5\)
B. \(\left| { - 3,5} \right| = 3,5.\)
C. \(\left| { - 3,5} \right| = \pm 3,5\)
D. \(\left| { - 3,5} \right| > 3,5.\)
Câu 7. Số nào trong các số dưới đây viết được dưới dạng số thập phân hữu hạn
A. \(\frac{{ - 7}}{{15}}\).
B. \(\frac{{ - 7}}{{24}}\).
C. \(\frac{{ - 5}}{{32}}\).
D. \(\frac{{12}}{{45}}\).
Câu 8. Giá trị của x trong đẳng thức - 0,6 = 1,4 là
A. 2 hoặc -2.
B. 0,6 hoặc -0,6.
C. 2.
D. -2.
Câu 9. Giá trị của đẳng thức\(\sqrt {2 + 3 + 4 + 3 + 4} \)
A. 16.
B. -16.
C. 4.
D. -4.
Câu 10. Cho ba đường thẳng phân biệt a, b, c biết \(a \bot c\)và \(c \bot b\). Kết luận nào đúng?
A. \(a//b.\)
B. \(c//b.\)
C. \(c \bot b.\)
D. \(c//a.\)
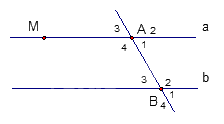
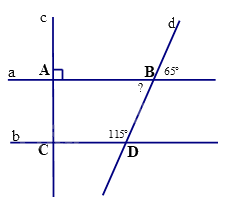
Câu 11. Cho hình vẽ số đo góc “?” ở hình vẽ là
A. 1300.
B. 650.
C. 900.
D. 500.
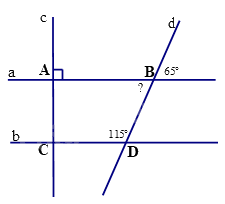
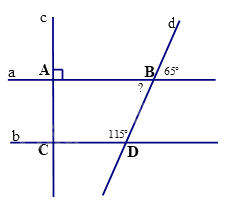
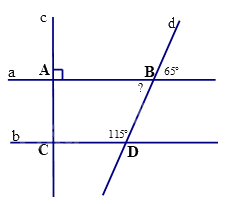
Câu 12. Cho hình vẽ số đo góc tại đỉnh C ở hình vẽ là
A. 1150.
B. 650.
C. 900.
D. 500.
PHẦN II. TỰ LUẬN (7 điểm)
Bài 1. ( 2,0 điểm)
1. So sánh: - 3,7634 và – 3,7654.
2. Thực hiện các phép tính sau
a. \(\frac{2}{9} - {\left( {\frac{1}{2}} \right)^2} + \frac{5}{{18}}\)
b. \(17\frac{1}{3}.\left( {\frac{{ - 5}}{7}} \right) - 10\frac{1}{3}.\left( {\frac{{ - 5}}{7}} \right)\)
Bài 2. ( 1,75 điểm) Tìm x, biết
a. x + 4,5 = 7,5
b. \(\frac{2}{3}.x + \frac{1}{2} = \frac{4}{9}\)
c. |x| - 0,7 = 1,3
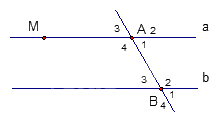
Bài 3. (2,25 điểm) Cho hình vẽ bên. Biết hai đường thẳng a và b song song với nhau và \(\widehat {{A_1}} = {70^0}\).
1. Hãy viết tên các cặp so le trong và các cặp góc trong cùng phía.
2. Tính số đo của \(\widehat {{A_3}};\,\widehat {{B_3}}\)
3. Kẻ đường thẳng c vuông góc với đường thẳng a tại M.
Chứng tỏ rằng: c \( \bot \) b
Bài 4. ( 1,0 điểm). So sánh A và B biết:
\(A = \frac{{{{2023}^{2023}} + 1}}{{{{2023}^{2024}} + 1}}\) và \(B = \frac{{{{2023}^{2022}} + 1}}{{{{2023}^{2023}} + 1}}\)
-------- Hết --------
Phần trắc nghiệm (3 điểm)
Câu 1: A | Câu 2: C | Câu 3: A | Câu 4: D | Câu 5: D | Câu 6: B |
Câu 7. C | Câu 8. A | Câu 9. C | Câu 10. A | Câu 11. B | Câu 12. C |
Câu 1. Chọn khẳng định đúng
A. \(\frac{3}{2} \in \mathbb{Q}.\) | B. \(\frac{3}{2} \in \mathbb{Z}\). |
C. \(\frac{{ - 9}}{5} \notin \mathbb{Q}\). | D. \( - 6 \in \mathbb{N}\). |
Phương pháp
Dựa vào khái niệm các tập hợp đã học.
Lời giải
\(\frac{3}{2}\) là số hữu tỉ nên \(\frac{3}{2} \in \mathbb{Q}.\)
Đáp án A.
Câu 2. Số hữu tỉ dương là
A. \(\frac{{ - 11}}{3}.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\) | B. \( - \frac{{12}}{5}.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\) |
C. \(\frac{{ - 5}}{{ - 7}}.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\) | D. \(\frac{{15}}{{ - 13}}.\) |
Phương pháp
Dựa vào khái niệm số hữu tỉ.
Lời giải
\(\frac{{ - 5}}{{ - 7}} = \frac{5}{7}\) nên là số hữu tỉ dương.
Đáp án C.
Câu 3. Kết quả phép tính \(\frac{3}{7} + \frac{4}{7}.\frac{{ - 21}}{{35}}\) là
A. \(\frac{3}{{35}}\). | B. \(\frac{{ - 21}}{{35}}\). |
C. \(\frac{{ - 11}}{{35}}\). | D. \(\frac{{11}}{{35}}\). |
Phương pháp
Dựa vào quy tắc tính với số hữu tỉ.
Lời giải
\(\begin{array}{l}\frac{3}{7} + \frac{4}{7}.\frac{{ - 21}}{{35}} = \frac{3}{7} + \frac{4}{7}.\frac{{ - 3}}{5} = \frac{3}{7} + \frac{{ - 12}}{{35}}\\ = \frac{{3.5 - 12}}{{35}} = \frac{3}{{35}}\end{array}\)
Đáp án A.
Câu 4. Giá trị của \(x\) trong phép tính \(\frac{2}{5} - x = \frac{1}{3}\) bằng
A. \(\frac{7}{{30}}.\) | B. \(\frac{{ - 1}}{{15}}.\) |
C. \(\frac{{11}}{{15}}.\) | D. \(\frac{1}{{15}}.\) |
Phương pháp
Sử dụng quy tắc trừ để tìm x.
Lời giải
\(\begin{array}{l}\frac{2}{5} - x = \frac{1}{3}\\x = \frac{2}{5} - \frac{1}{3}\\x = \frac{1}{{15}}\end{array}\).
Vậy \(x = \frac{1}{{15}}\)
Đáp án D.
Câu 5. Căn bậc hai số học của 81 là
A. 9 và -9 | B. \(\frac{{ - 1}}{{81}}.\) |
C. \( - 9.\) | D. \(9.\) |
Phương pháp
Dựa vào kiến thức về căn bậc hai số học.
Lời giải
Căn bậc hai số học của 81 là 9.
Đáp án D.
Câu 6. Khẳng định đúng là
A. \(\left| { - 3,5} \right| = - 3,5\) | B. \(\left| { - 3,5} \right| = 3,5.\) |
C. \(\left| { - 3,5} \right| = \pm 3,5\) | D. \(\left| { - 3,5} \right| > 3,5.\) |
Phương pháp
Dựa vào kiến thức về giá trị tuyệt đối.
Lời giải
Vì -3,5 < 0 nên |-3,5| = - (-3,5) = 3,5.
Đáp án B.
Câu 7. Số nào trong các số dưới đây viết được dưới dạng số thập phân hữu hạn
A. \(\frac{{ - 7}}{{15}}\). | B. \(\frac{{ - 7}}{{24}}\). |
C. \(\frac{{ - 5}}{{32}}\). | D. \(\frac{{12}}{{45}}\). |
Phương pháp
Dựa vào kiến thức về số thập phân hữu hạn.
Lời giải
\(\frac{{ - 7}}{{15}} = - 0,4(6)\).
\(\frac{{ - 7}}{{24}} = - 0,291(6)\).
\(\frac{{ - 5}}{{32}} = - 0,15625\).
\(\frac{{12}}{{45}} = 0,2(6)\).
Đáp án C.
Câu 8. Giá trị của x trong đẳng thức |x| - 0,6 = 1,4 là
A. 2 hoặc -2. | B. 0,6 hoặc -0,6. |
C. 2. | D. -2. |
Phương pháp
Sử dụng quy tắc cộng và kiến thức về giá trị tuyệt đối để tìm x.
Lời giải
|x| - 0,6 = 1,4
|x| = 1,4 + 0,6
|x| = 2
Vậy x = 2 hoặc x = -2.
Đáp án A.
Câu 9. Giá trị của đẳng thức \(\sqrt {2 + 3 + 4 + 3 + 4} \)
A. 16. | B. -16. |
C. 4. | D. -4. |
Phương pháp
Sử dụng quy tắc cộng và kiến thức về căn bậc hai để tính giá trị của đẳng thức.
Lời giải
\(\sqrt {2 + 3 + 4 + 3 + 4} = \sqrt {16} = 4\)
Đáp án C.
Câu 10. Cho ba đường thẳng phân biệt a, b, c biết \(a \bot c\)và \(c \bot b\). Kết luận nào đúng?
A. \(a//b.\) | B. \(c//b.\) |
C. \(c \bot b.\) | D. \(c//a.\) |
Phương pháp
Dựa vào kiến thức về hai đường thẳng song song.
Lời giải
Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song. Vậy nếu biết \(a \bot c\)và \(c \bot b\) ta suy ra a // b.
Đáp án A.
Câu 11. Cho hình vẽ số đo góc “?” ở hình vẽ là
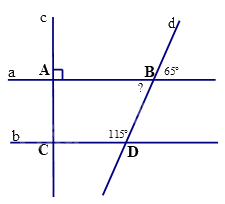
A. 1300. | B. 650. |
C. 900. | D. 500. |
Phương pháp
Dựa vào tính chất hai góc đối đỉnh.
Lời giải
Quan sát hình vẽ, ta thấy \(? = {65^0}\).
Đáp án D.
Câu 12. Cho hình vẽ số đo góc tại đỉnh C ở hình vẽ là
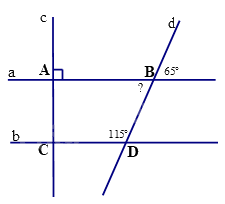
A. 1150. | B. 650. |
C. 900. | D. 500. |
Phương pháp
Tính số đo góc dBA, so sánh với góc BDC để xét AB // CD.
Lời giải
Ta có góc dBA kề bù với góc 650 nên \(\widehat {dBA} = {180^0} - {65^0} = {115^0} = \widehat {BDC}\).
Mà góc dBA và góc BDC là hai góc đồng vị nên AB // CD.
Do đó, \(\widehat C = \widehat A = {90^0}\)(hai góc đồng vị).
Đáp án C.
Phần tự luận.
Bài 1. ( 2,0 điểm)
1. So sánh: - 3,7634 và – 3,7654.
2. Thực hiện các phép tính sau
a. \(\frac{2}{9} - {\left( {\frac{1}{2}} \right)^2} + \frac{5}{{18}}\) | b. \(17\frac{1}{3}.\left( {\frac{{ - 5}}{7}} \right) - 10\frac{1}{3}.\left( {\frac{{ - 5}}{7}} \right)\) |
Phương pháp
1. So sánh 3,7634 với 3,7654, số nào lớn hơn thì thêm dấu trừ sẽ là số nhỏ hơn.
2. Sử dụng các quy tắc tính toán với số hữu tỉ để thực hiện phép tính.
Lời giải
1. Ta có: 3,7634 < 3,7654 nên – 3,7634 > - 3,7654.
2.
a. \(\frac{2}{9} - {\left( {\frac{1}{2}} \right)^2} + \frac{5}{{18}}\)
\(\begin{array}{l}\frac{2}{9} - \frac{1}{4} + \frac{5}{{18}}\\ = \left( {\frac{2}{9} + \frac{5}{{18}}} \right) - \frac{1}{4}\\ = \frac{1}{2} - \frac{1}{4}\\ = \frac{1}{4}\end{array}\)
b. \(17\frac{1}{3}.\left( {\frac{{ - 5}}{7}} \right) - 10\frac{1}{3}.\left( {\frac{{ - 5}}{7}} \right)\)
\(\begin{array}{l}\left( {17\frac{1}{3} - 10\frac{1}{3}} \right).\left( {\frac{{ - 5}}{7}} \right)\\ = 7.\left( {\frac{{ - 5}}{7}} \right)\\ = - 5\end{array}\)
Bài 2. ( 1,75 điểm) Tìm x, biết
a. x + 4,5 = 7,5 | b. \(\frac{2}{3}.x + \frac{1}{2} = \frac{4}{9}\) | c. |x| - 0,7 = 1,3 |
Phương pháp
Dựa vào quy tắc tính để tìm x.
Lời giải
a. x + 4,5 = 7,5
x = 7,5 – 4,5
x = 3
Vậy x = 3.
b. \(\frac{2}{3}.x + \frac{1}{2} = \frac{4}{9}\)
\(\begin{array}{l}\frac{2}{3}.x = \frac{4}{9} - \frac{1}{2}\\\frac{2}{3}x = - \frac{1}{{18}}\\x = - \frac{1}{{18}}:\frac{2}{3}\\x = - \frac{1}{{12}}\end{array}\)
Vậy \(x = - \frac{1}{{12}}\).
c. |x| - 0,7 = 1,3
|x| = 1,3 + 0,7
|x| = 2
x = -2 hoặc x = 2.
Vậy x = -2 hoặc x = 2.
Bài 3. (2,25 điểm) Cho hình vẽ bên. Biết hai đường thẳng a và b song song với nhau và \(\widehat {{A_1}} = {70^0}\).
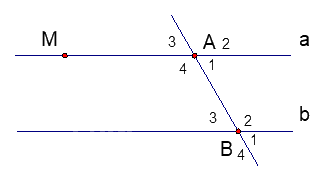
1. Hãy viết tên các cặp so le trong và các cặp góc trong cùng phía.
2. Tính số đo của \(\widehat {{A_3}};\,\widehat {{B_3}}\)
3. Kẻ đường thẳng c vuông góc với đường thẳng a tại M.
Chứng tỏ rằng: c \( \bot \) b
Phương pháp
1. Dựa vào tính chất của hai đường thẳng song song.
2. Dựa vào hai góc đối đỉnh và tính chất các góc của hai đường thẳng song song.
3. Dựa vào quan hệ giữa tính vuông góc và song song.
Lời giải
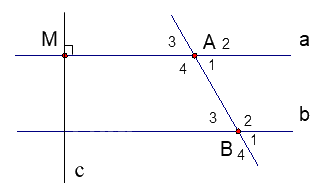
1. Ta có a // b nên các cặp góc so le trong là: \(\widehat {{A_1}}\) và \(\widehat {{B_3}}\), \(\widehat {{A_4}}\) và \(\widehat {{B_2}}\).
Các cặp góc trong cùng phía là \(\widehat {{A_1}}\) và \(\widehat {{B_2}}\), \(\widehat {{A_4}}\) và \(\widehat {{B_3}}\).
2. Ta có \(\widehat {{A_1}}\) và \(\;\widehat {{A_3}}\) là hai góc đối đỉnh nên \(\widehat {{A_1}}\) = \(\;\widehat {{A_3}}\) = 700.
Vì a // b nên ta có \(\widehat {{A_3}} = \widehat {{B_3}}\) (hai góc đồng vị) nên \(\;\widehat {{A_3}}\)= \(\widehat {{B_3}}\) = 700.
3. Vì a \( \bot \) c và a // b nên b \( \bot \) c (mối quan hệ giữa tính vuông góc và song song.
Bài 4. ( 1,0 điểm). So sánh A và B biết:
\(A = \frac{{{{2023}^{2023}} + 1}}{{{{2023}^{2024}} + 1}}\) và \(B = \frac{{{{2023}^{2022}} + 1}}{{{{2023}^{2023}} + 1}}\)
Phương pháp
Nhân cả A và B với 2023, đưa A và B về so sánh 2 phân số cùng tử, từ đó so sánh được A và B.
Lời giải
Nhân A với 2023, ta được: \(2023A = \frac{{2023\left( {{{2023}^{2023}} + 1} \right)}}{{{{2023}^{2024}} + 1}} = \frac{{{{2023}^{2024}} + 2023}}{{{{2023}^{2024}} + 1}} = 1 + \frac{{2022}}{{{{2023}^{2024}} + 1}}\).
Nhân B với 2023, ta được: \(2023B = \frac{{2023\left( {{{2023}^{2022}} + 1} \right)}}{{{{2023}^{2023}} + 1}} = \frac{{{{2023}^{2023}} + 2023}}{{{{2023}^{2023}} + 1}} = 1 + \frac{{2022}}{{{{2023}^{2023}} + 1}}\).
Ta có:
\(\begin{array}{l}{2023^{2024}} > {2023^{2023}}\\{2023^{2024}} + 1 > {2023^{2023}} + 1\\\frac{1}{{{{2023}^{2024}} + 1}} < \frac{1}{{{{2023}^{2023}} + 1}}\\\frac{{2022}}{{{{2023}^{2024}} + 1}} < \frac{{2022}}{{{{2023}^{2023}} + 1}}\\1 + \frac{{2022}}{{{{2023}^{2024}} + 1}} < 1 + \frac{{2022}}{{{{2023}^{2023}} + 1}}\\2023A < 2023B\\A < B\end{array}\)
Vậy A < B.
Tải về
Phần trắc nghiệm (3 điểm)
Câu 1. Chọn khẳng định đúng
A. \(\frac{3}{2} \in \mathbb{Q}.\)
B. \(\frac{3}{2} \in \mathbb{Z}\).
C. \(\frac{{ - 9}}{5} \notin \mathbb{Q}\).
D. \( - 6 \in \mathbb{N}\).
Câu 2. Số hữu tỉ dương là
A. \(\frac{{ - 11}}{3}.\)
B. \( - \frac{{12}}{5}.\)
C. \(\frac{{ - 5}}{{ - 7}}.\)
D. \(\frac{{15}}{{ - 13}}.\)
Câu 3. Kết quả phép tính \(\frac{3}{7} + \frac{4}{7}.\frac{{ - 21}}{{35}}\) là
A. \(\frac{3}{{35}}\).
B. \(\frac{{ - 21}}{{35}}\).
C. \(\frac{{ - 11}}{{35}}\).
D. \(\frac{{11}}{{35}}\).
Câu 4. Giá trị của \(x\) trong phép tính \(\frac{2}{5} - x = \frac{1}{3}\) bằng
A. \(\frac{7}{{30}}.\)
B. \(\frac{{ - 1}}{{15}}.\)
C. \(\frac{{11}}{{15}}.\)
D. \(\frac{1}{{15}}.\)
Câu 5. Căn bậc hai số học của 81 là
A. 9 và -9
B. \(\frac{{ - 1}}{{81}}.\)
C. \( - 9.\)
D. \(9.\)
Câu 6. Khẳng định đúng là
A. \(\left| { - 3,5} \right| = - 3,5\)
B. \(\left| { - 3,5} \right| = 3,5.\)
C. \(\left| { - 3,5} \right| = \pm 3,5\)
D. \(\left| { - 3,5} \right| > 3,5.\)
Câu 7. Số nào trong các số dưới đây viết được dưới dạng số thập phân hữu hạn
A. \(\frac{{ - 7}}{{15}}\).
B. \(\frac{{ - 7}}{{24}}\).
C. \(\frac{{ - 5}}{{32}}\).
D. \(\frac{{12}}{{45}}\).
Câu 8. Giá trị của x trong đẳng thức - 0,6 = 1,4 là
A. 2 hoặc -2.
B. 0,6 hoặc -0,6.
C. 2.
D. -2.
Câu 9. Giá trị của đẳng thức\(\sqrt {2 + 3 + 4 + 3 + 4} \)
A. 16.
B. -16.
C. 4.
D. -4.
Câu 10. Cho ba đường thẳng phân biệt a, b, c biết \(a \bot c\)và \(c \bot b\). Kết luận nào đúng?
A. \(a//b.\)
B. \(c//b.\)
C. \(c \bot b.\)
D. \(c//a.\)
Câu 11. Cho hình vẽ số đo góc “?” ở hình vẽ là
A. 1300.
B. 650.
C. 900.
D. 500.
Câu 12. Cho hình vẽ số đo góc tại đỉnh C ở hình vẽ là
A. 1150.
B. 650.
C. 900.
D. 500.
PHẦN II. TỰ LUẬN (7 điểm)
Bài 1. ( 2,0 điểm)
1. So sánh: - 3,7634 và – 3,7654.
2. Thực hiện các phép tính sau
a. \(\frac{2}{9} - {\left( {\frac{1}{2}} \right)^2} + \frac{5}{{18}}\)
b. \(17\frac{1}{3}.\left( {\frac{{ - 5}}{7}} \right) - 10\frac{1}{3}.\left( {\frac{{ - 5}}{7}} \right)\)
Bài 2. ( 1,75 điểm) Tìm x, biết
a. x + 4,5 = 7,5
b. \(\frac{2}{3}.x + \frac{1}{2} = \frac{4}{9}\)
c. |x| - 0,7 = 1,3
Bài 3. (2,25 điểm) Cho hình vẽ bên. Biết hai đường thẳng a và b song song với nhau và \(\widehat {{A_1}} = {70^0}\).
1. Hãy viết tên các cặp so le trong và các cặp góc trong cùng phía.
2. Tính số đo của \(\widehat {{A_3}};\,\widehat {{B_3}}\)
3. Kẻ đường thẳng c vuông góc với đường thẳng a tại M.
Chứng tỏ rằng: c \( \bot \) b
Bài 4. ( 1,0 điểm). So sánh A và B biết:
\(A = \frac{{{{2023}^{2023}} + 1}}{{{{2023}^{2024}} + 1}}\) và \(B = \frac{{{{2023}^{2022}} + 1}}{{{{2023}^{2023}} + 1}}\)
-------- Hết --------
Phần trắc nghiệm (3 điểm)
Câu 1: A | Câu 2: C | Câu 3: A | Câu 4: D | Câu 5: D | Câu 6: B |
Câu 7. C | Câu 8. A | Câu 9. C | Câu 10. A | Câu 11. B | Câu 12. C |
Câu 1. Chọn khẳng định đúng
A. \(\frac{3}{2} \in \mathbb{Q}.\) | B. \(\frac{3}{2} \in \mathbb{Z}\). |
C. \(\frac{{ - 9}}{5} \notin \mathbb{Q}\). | D. \( - 6 \in \mathbb{N}\). |
Phương pháp
Dựa vào khái niệm các tập hợp đã học.
Lời giải
\(\frac{3}{2}\) là số hữu tỉ nên \(\frac{3}{2} \in \mathbb{Q}.\)
Đáp án A.
Câu 2. Số hữu tỉ dương là
A. \(\frac{{ - 11}}{3}.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\) | B. \( - \frac{{12}}{5}.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\) |
C. \(\frac{{ - 5}}{{ - 7}}.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\) | D. \(\frac{{15}}{{ - 13}}.\) |
Phương pháp
Dựa vào khái niệm số hữu tỉ.
Lời giải
\(\frac{{ - 5}}{{ - 7}} = \frac{5}{7}\) nên là số hữu tỉ dương.
Đáp án C.
Câu 3. Kết quả phép tính \(\frac{3}{7} + \frac{4}{7}.\frac{{ - 21}}{{35}}\) là
A. \(\frac{3}{{35}}\). | B. \(\frac{{ - 21}}{{35}}\). |
C. \(\frac{{ - 11}}{{35}}\). | D. \(\frac{{11}}{{35}}\). |
Phương pháp
Dựa vào quy tắc tính với số hữu tỉ.
Lời giải
\(\begin{array}{l}\frac{3}{7} + \frac{4}{7}.\frac{{ - 21}}{{35}} = \frac{3}{7} + \frac{4}{7}.\frac{{ - 3}}{5} = \frac{3}{7} + \frac{{ - 12}}{{35}}\\ = \frac{{3.5 - 12}}{{35}} = \frac{3}{{35}}\end{array}\)
Đáp án A.
Câu 4. Giá trị của \(x\) trong phép tính \(\frac{2}{5} - x = \frac{1}{3}\) bằng
A. \(\frac{7}{{30}}.\) | B. \(\frac{{ - 1}}{{15}}.\) |
C. \(\frac{{11}}{{15}}.\) | D. \(\frac{1}{{15}}.\) |
Phương pháp
Sử dụng quy tắc trừ để tìm x.
Lời giải
\(\begin{array}{l}\frac{2}{5} - x = \frac{1}{3}\\x = \frac{2}{5} - \frac{1}{3}\\x = \frac{1}{{15}}\end{array}\).
Vậy \(x = \frac{1}{{15}}\)
Đáp án D.
Câu 5. Căn bậc hai số học của 81 là
A. 9 và -9 | B. \(\frac{{ - 1}}{{81}}.\) |
C. \( - 9.\) | D. \(9.\) |
Phương pháp
Dựa vào kiến thức về căn bậc hai số học.
Lời giải
Căn bậc hai số học của 81 là 9.
Đáp án D.
Câu 6. Khẳng định đúng là
A. \(\left| { - 3,5} \right| = - 3,5\) | B. \(\left| { - 3,5} \right| = 3,5.\) |
C. \(\left| { - 3,5} \right| = \pm 3,5\) | D. \(\left| { - 3,5} \right| > 3,5.\) |
Phương pháp
Dựa vào kiến thức về giá trị tuyệt đối.
Lời giải
Vì -3,5 < 0 nên |-3,5| = - (-3,5) = 3,5.
Đáp án B.
Câu 7. Số nào trong các số dưới đây viết được dưới dạng số thập phân hữu hạn
A. \(\frac{{ - 7}}{{15}}\). | B. \(\frac{{ - 7}}{{24}}\). |
C. \(\frac{{ - 5}}{{32}}\). | D. \(\frac{{12}}{{45}}\). |
Phương pháp
Dựa vào kiến thức về số thập phân hữu hạn.
Lời giải
\(\frac{{ - 7}}{{15}} = - 0,4(6)\).
\(\frac{{ - 7}}{{24}} = - 0,291(6)\).
\(\frac{{ - 5}}{{32}} = - 0,15625\).
\(\frac{{12}}{{45}} = 0,2(6)\).
Đáp án C.
Câu 8. Giá trị của x trong đẳng thức |x| - 0,6 = 1,4 là
A. 2 hoặc -2. | B. 0,6 hoặc -0,6. |
C. 2. | D. -2. |
Phương pháp
Sử dụng quy tắc cộng và kiến thức về giá trị tuyệt đối để tìm x.
Lời giải
|x| - 0,6 = 1,4
|x| = 1,4 + 0,6
|x| = 2
Vậy x = 2 hoặc x = -2.
Đáp án A.
Câu 9. Giá trị của đẳng thức \(\sqrt {2 + 3 + 4 + 3 + 4} \)
A. 16. | B. -16. |
C. 4. | D. -4. |
Phương pháp
Sử dụng quy tắc cộng và kiến thức về căn bậc hai để tính giá trị của đẳng thức.
Lời giải
\(\sqrt {2 + 3 + 4 + 3 + 4} = \sqrt {16} = 4\)
Đáp án C.
Câu 10. Cho ba đường thẳng phân biệt a, b, c biết \(a \bot c\)và \(c \bot b\). Kết luận nào đúng?
A. \(a//b.\) | B. \(c//b.\) |
C. \(c \bot b.\) | D. \(c//a.\) |
Phương pháp
Dựa vào kiến thức về hai đường thẳng song song.
Lời giải
Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song. Vậy nếu biết \(a \bot c\)và \(c \bot b\) ta suy ra a // b.
Đáp án A.
Câu 11. Cho hình vẽ số đo góc “?” ở hình vẽ là
A. 1300. | B. 650. |
C. 900. | D. 500. |
Phương pháp
Dựa vào tính chất hai góc đối đỉnh.
Lời giải
Quan sát hình vẽ, ta thấy \(? = {65^0}\).
Đáp án D.
Câu 12. Cho hình vẽ số đo góc tại đỉnh C ở hình vẽ là
A. 1150. | B. 650. |
C. 900. | D. 500. |
Phương pháp
Tính số đo góc dBA, so sánh với góc BDC để xét AB // CD.
Lời giải
Ta có góc dBA kề bù với góc 650 nên \(\widehat {dBA} = {180^0} - {65^0} = {115^0} = \widehat {BDC}\).
Mà góc dBA và góc BDC là hai góc đồng vị nên AB // CD.
Do đó, \(\widehat C = \widehat A = {90^0}\)(hai góc đồng vị).
Đáp án C.
Phần tự luận.
Bài 1. ( 2,0 điểm)
1. So sánh: - 3,7634 và – 3,7654.
2. Thực hiện các phép tính sau
a. \(\frac{2}{9} - {\left( {\frac{1}{2}} \right)^2} + \frac{5}{{18}}\) | b. \(17\frac{1}{3}.\left( {\frac{{ - 5}}{7}} \right) - 10\frac{1}{3}.\left( {\frac{{ - 5}}{7}} \right)\) |
Phương pháp
1. So sánh 3,7634 với 3,7654, số nào lớn hơn thì thêm dấu trừ sẽ là số nhỏ hơn.
2. Sử dụng các quy tắc tính toán với số hữu tỉ để thực hiện phép tính.
Lời giải
1. Ta có: 3,7634 < 3,7654 nên – 3,7634 > - 3,7654.
2.
a. \(\frac{2}{9} - {\left( {\frac{1}{2}} \right)^2} + \frac{5}{{18}}\)
\(\begin{array}{l}\frac{2}{9} - \frac{1}{4} + \frac{5}{{18}}\\ = \left( {\frac{2}{9} + \frac{5}{{18}}} \right) - \frac{1}{4}\\ = \frac{1}{2} - \frac{1}{4}\\ = \frac{1}{4}\end{array}\)
b. \(17\frac{1}{3}.\left( {\frac{{ - 5}}{7}} \right) - 10\frac{1}{3}.\left( {\frac{{ - 5}}{7}} \right)\)
\(\begin{array}{l}\left( {17\frac{1}{3} - 10\frac{1}{3}} \right).\left( {\frac{{ - 5}}{7}} \right)\\ = 7.\left( {\frac{{ - 5}}{7}} \right)\\ = - 5\end{array}\)
Bài 2. ( 1,75 điểm) Tìm x, biết
a. x + 4,5 = 7,5 | b. \(\frac{2}{3}.x + \frac{1}{2} = \frac{4}{9}\) | c. |x| - 0,7 = 1,3 |
Phương pháp
Dựa vào quy tắc tính để tìm x.
Lời giải
a. x + 4,5 = 7,5
x = 7,5 – 4,5
x = 3
Vậy x = 3.
b. \(\frac{2}{3}.x + \frac{1}{2} = \frac{4}{9}\)
\(\begin{array}{l}\frac{2}{3}.x = \frac{4}{9} - \frac{1}{2}\\\frac{2}{3}x = - \frac{1}{{18}}\\x = - \frac{1}{{18}}:\frac{2}{3}\\x = - \frac{1}{{12}}\end{array}\)
Vậy \(x = - \frac{1}{{12}}\).
c. |x| - 0,7 = 1,3
|x| = 1,3 + 0,7
|x| = 2
x = -2 hoặc x = 2.
Vậy x = -2 hoặc x = 2.
Bài 3. (2,25 điểm) Cho hình vẽ bên. Biết hai đường thẳng a và b song song với nhau và \(\widehat {{A_1}} = {70^0}\).
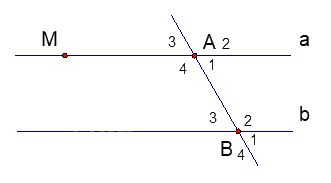
1. Hãy viết tên các cặp so le trong và các cặp góc trong cùng phía.
2. Tính số đo của \(\widehat {{A_3}};\,\widehat {{B_3}}\)
3. Kẻ đường thẳng c vuông góc với đường thẳng a tại M.
Chứng tỏ rằng: c \( \bot \) b
Phương pháp
1. Dựa vào tính chất của hai đường thẳng song song.
2. Dựa vào hai góc đối đỉnh và tính chất các góc của hai đường thẳng song song.
3. Dựa vào quan hệ giữa tính vuông góc và song song.
Lời giải
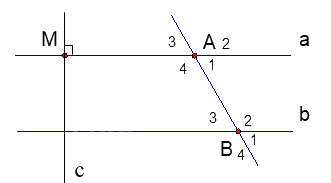
1. Ta có a // b nên các cặp góc so le trong là: \(\widehat {{A_1}}\) và \(\widehat {{B_3}}\), \(\widehat {{A_4}}\) và \(\widehat {{B_2}}\).
Các cặp góc trong cùng phía là \(\widehat {{A_1}}\) và \(\widehat {{B_2}}\), \(\widehat {{A_4}}\) và \(\widehat {{B_3}}\).
2. Ta có \(\widehat {{A_1}}\) và \(\;\widehat {{A_3}}\) là hai góc đối đỉnh nên \(\widehat {{A_1}}\) = \(\;\widehat {{A_3}}\) = 700.
Vì a // b nên ta có \(\widehat {{A_3}} = \widehat {{B_3}}\) (hai góc đồng vị) nên \(\;\widehat {{A_3}}\)= \(\widehat {{B_3}}\) = 700.
3. Vì a \( \bot \) c và a // b nên b \( \bot \) c (mối quan hệ giữa tính vuông góc và song song.
Bài 4. ( 1,0 điểm). So sánh A và B biết:
\(A = \frac{{{{2023}^{2023}} + 1}}{{{{2023}^{2024}} + 1}}\) và \(B = \frac{{{{2023}^{2022}} + 1}}{{{{2023}^{2023}} + 1}}\)
Phương pháp
Nhân cả A và B với 2023, đưa A và B về so sánh 2 phân số cùng tử, từ đó so sánh được A và B.
Lời giải
Nhân A với 2023, ta được: \(2023A = \frac{{2023\left( {{{2023}^{2023}} + 1} \right)}}{{{{2023}^{2024}} + 1}} = \frac{{{{2023}^{2024}} + 2023}}{{{{2023}^{2024}} + 1}} = 1 + \frac{{2022}}{{{{2023}^{2024}} + 1}}\).
Nhân B với 2023, ta được: \(2023B = \frac{{2023\left( {{{2023}^{2022}} + 1} \right)}}{{{{2023}^{2023}} + 1}} = \frac{{{{2023}^{2023}} + 2023}}{{{{2023}^{2023}} + 1}} = 1 + \frac{{2022}}{{{{2023}^{2023}} + 1}}\).
Ta có:
\(\begin{array}{l}{2023^{2024}} > {2023^{2023}}\\{2023^{2024}} + 1 > {2023^{2023}} + 1\\\frac{1}{{{{2023}^{2024}} + 1}} < \frac{1}{{{{2023}^{2023}} + 1}}\\\frac{{2022}}{{{{2023}^{2024}} + 1}} < \frac{{2022}}{{{{2023}^{2023}} + 1}}\\1 + \frac{{2022}}{{{{2023}^{2024}} + 1}} < 1 + \frac{{2022}}{{{{2023}^{2023}} + 1}}\\2023A < 2023B\\A < B\end{array}\)
Vậy A < B.
Đề thi giữa kì 1 Toán 7 - Đề số 8 chương trình Kết nối tri thức là một bài kiểm tra quan trọng giúp đánh giá mức độ nắm vững kiến thức của học sinh sau một thời gian học tập. Đề thi bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính đã được học trong chương trình. Việc làm quen với cấu trúc đề thi và luyện tập giải các bài tập tương tự là rất cần thiết để đạt kết quả tốt.
Đề thi thường bao gồm các nội dung sau:
Để giải các bài tập về số hữu tỉ, học sinh cần nắm vững các quy tắc cộng, trừ, nhân, chia số hữu tỉ. Ví dụ:
Tính: (-2/3) + (1/2)
Giải:
(-2/3) + (1/2) = (-4/6) + (3/6) = -1/6
Để giải phương trình bậc nhất một ẩn, học sinh cần thực hiện các bước sau:
Ví dụ:
Giải phương trình: 2x - 5 = 3
Giải:
2x - 5 = 3
2x = 8
x = 4
Các bài tập về hình học thường yêu cầu học sinh vận dụng các kiến thức về góc, đường thẳng song song, tam giác, tứ giác để chứng minh các mối quan hệ hoặc tính toán các đại lượng hình học.
Để đạt kết quả tốt trong kỳ thi giữa kì 1, học sinh cần:
Làm đề thi thử giúp học sinh:
Giaitoan.edu.vn cung cấp đầy đủ các tài liệu học tập Toán 7, bao gồm:
Đề thi giữa kì 1 Toán 7 - Đề số 8 - Kết nối tri thức là một cơ hội tốt để học sinh đánh giá năng lực của mình và chuẩn bị cho các kỳ thi tiếp theo. Hãy luyện tập chăm chỉ và sử dụng các tài liệu học tập uy tín để đạt kết quả tốt nhất!