Chào mừng các em học sinh lớp 7 đến với đề thi giữa kì 1 Toán 7 - Đề số 9 chương trình Kết nối tri thức.
Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong giai đoạn giữa kì 1.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán!
Phần trắc nghiệm (3 điểm) Câu 1: Số đối của số hữu tỉ ( - 0,25) là
Phần trắc nghiệm (3 điểm)
Câu 1: Số đối của số hữu tỉ \( - 0,25\) là
A. \( - 0,25.\)
B. \(\frac{{ - 1}}{4}.\)
C. \( - 4.\)
D. \(0,25.\)
Câu 2: Trong các số sau, số nào là số hữu tỉ âm?
A. \(\frac{0}{{ - 2}}\)
B. \(\frac{{ - 2}}{{ - 1}}\)
C. \( - \frac{1}{2}\)
D. \(\frac{{ - \left( { - 2} \right)}}{3}\)
Câu 3: Khi biểu diễu số hữu tỉ a và b trên trục số nằm ngang ta thấy điểm a nằm bên phải điểm b thì
A. \(a < b.\)
B. \(a > b.\)
C. \(a = b.\)
D. \(a = - b.\)
Câu 4: Kết quả của phép tính \({7^{10}}:7\) viết dưới dạng lũy thừa là
A. \({7^9}.\)
B. \({7^{11}}.\)
C. \({7^{10}}.\)
D. \({1^{10}}.\)
Câu 5: Với \(a,b,c\) là ba số hữu tỉ bất kì, nếu \(a - b = c\) thì
A. \(a = b + c.\)
B. \(a = - b + c.\)
C. \(a = b - c.\)
D. \(a = - b - c.\)
Câu 6: Với \(x,y,z\) là ba số hữu tỉ bất kì, sau khi bỏ ngoặc ta được \(x - \left( {y + z} \right)\) bằng
A. \(x - y + z.\)
B. \(x - y - z.\)
C. \(x + y - z.\)
D. \(x + y + z.\)
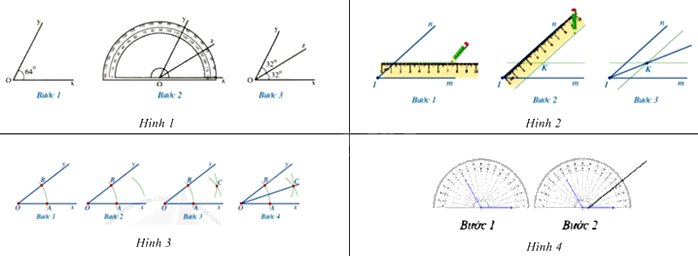
Câu 7: Trong các hình dưới đây, hình nào mô tả không đúng cách vẽ tia phân giác của một góc?
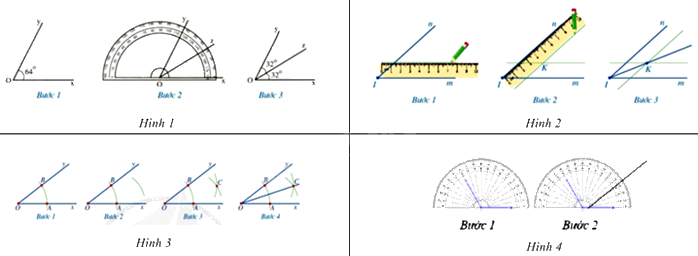
A. Hình 1.
B. Hình 2.
C. Hình 3.
D. Hình 4.
Sử dụng Hình 5 để trả lời các câu hỏi từ Câu 8 đến Câu 10.
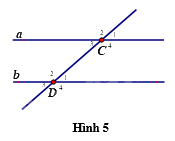
Câu 8: Góc \({C_4}\) kề bù với góc nào?
A. Góc\({D_4}.\)
B. Góc\({D_2}.\)
C. Góc\({C_2}.\)
D. Góc\({C_1}.\)
Câu 9: Góc \({D_1}\) đối đỉnh với góc nào?
A. Góc\({D_1}\).
B. Góc\({D_2}\).
C. Góc \({D_3}\).
D. Góc\({D_4}\).
Câu 10: Nếu \(a{\rm{//}}b\) thì số đo góc \({D_1}\) bằng số đo
A. góc \({C_1}\).
B. góc \({C_2}\).
C. góc \({C_4}\).
D. góc \({D_2}\).
Câu 11: Qua một điểm nằm ngoài một đường thẳng, có bao nhiêu đường thẳng song song với đường thẳng đó?
A. \(0.\)
B. \(1.\)
C. \(2.\)
D. Vô số.
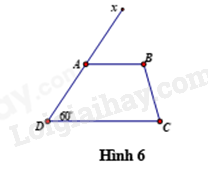
Câu 12: Cho Hình 6, cần thêm điều kiện gì thì \(AB{\rm{//}}DC\)?
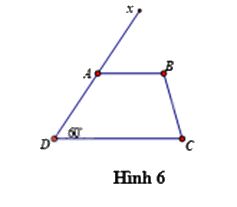
A. \(\widehat {BCD} = 60^\circ \)
B. \(\widehat {BCD} = 120^\circ \)
C. \(\widehat {BAD} = 60^\circ \)
D. \(\widehat {xAB} = 60^\circ \)
Phần tự luận (7 điểm)
Bài 1: (0,5 điểm) So sánh hai số hữu tỉ sau: \(0,25\) và \(\frac{1}{3}\)
Bài 2: (2,0 điểm) Thực hiện phép tính:
a) \(\left( { - 0,25} \right).40\; + 3\)
b) \(\frac{1}{7} \cdot \frac{{ - 3}}{8} + \frac{{ - 13}}{8} \cdot \frac{1}{7}\)
c) \(\left[ {\left( {\frac{2}{3} - \frac{1}{4}} \right) + {{\left( { - 2} \right)}^2}.3} \right] - 1\)
Bài 3: (2,0 điểm) Tìm x, biết:
a) \(x - 4 = \frac{1}{2}\)
b) \(2.\left( {x - 1} \right) = {3^3} - 1\)
Bài 4: (1,5 điểm)
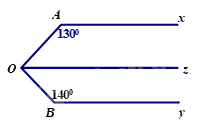
Hình 7
Cho Hình 7, biết \(Ax{\rm{//}}Oz\) và \(Ax{\rm{//}}By\).
a) Tính số đo góc \(AOz.\)
b) Chứng tỏ rằng góc \(AOB\) là góc vuông.
c) Tia \(Oz\) có là tia phân giác của góc \(AOB\) không? Vì sao?
Bài 5: (1,0 điểm)
Để nâng cao hiệu quả phòng chống dịch bệnh, học sinh phải thực hiện việc test nhanh Covid trước khi đến trường. Giá ban đầu để test mẫu gộp là \(40000\)đồng/1 học sinh, mẫu đơn là \(100000\)đồng/1 học sinh. Do lớp 7A test sau ngày 21/2/2022 nên được giảm giá 30%. Tính chi phí test nhanh Covid của lớp 7A biết có \(13\) em test mẫu gộp, \(22\) em test mẫu đơn.
-------- Hết --------
Tải về
Phần trắc nghiệm (3 điểm)
Câu 1: Số đối của số hữu tỉ \( - 0,25\) là
A. \( - 0,25.\)
B. \(\frac{{ - 1}}{4}.\)
C. \( - 4.\)
D. \(0,25.\)
Câu 2: Trong các số sau, số nào là số hữu tỉ âm?
A. \(\frac{0}{{ - 2}}\)
B. \(\frac{{ - 2}}{{ - 1}}\)
C. \( - \frac{1}{2}\)
D. \(\frac{{ - \left( { - 2} \right)}}{3}\)
Câu 3: Khi biểu diễu số hữu tỉ a và b trên trục số nằm ngang ta thấy điểm a nằm bên phải điểm b thì
A. \(a < b.\)
B. \(a > b.\)
C. \(a = b.\)
D. \(a = - b.\)
Câu 4: Kết quả của phép tính \({7^{10}}:7\) viết dưới dạng lũy thừa là
A. \({7^9}.\)
B. \({7^{11}}.\)
C. \({7^{10}}.\)
D. \({1^{10}}.\)
Câu 5: Với \(a,b,c\) là ba số hữu tỉ bất kì, nếu \(a - b = c\) thì
A. \(a = b + c.\)
B. \(a = - b + c.\)
C. \(a = b - c.\)
D. \(a = - b - c.\)
Câu 6: Với \(x,y,z\) là ba số hữu tỉ bất kì, sau khi bỏ ngoặc ta được \(x - \left( {y + z} \right)\) bằng
A. \(x - y + z.\)
B. \(x - y - z.\)
C. \(x + y - z.\)
D. \(x + y + z.\)
Câu 7: Trong các hình dưới đây, hình nào mô tả không đúng cách vẽ tia phân giác của một góc?
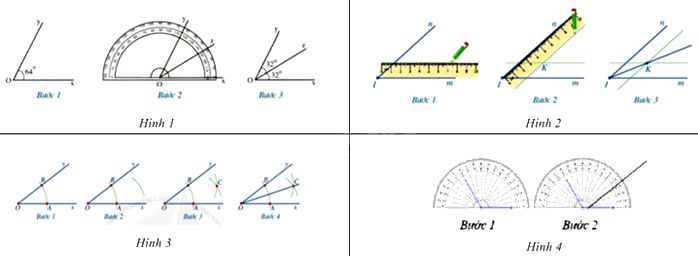
A. Hình 1.
B. Hình 2.
C. Hình 3.
D. Hình 4.
Sử dụng Hình 5 để trả lời các câu hỏi từ Câu 8 đến Câu 10.
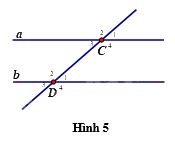
Câu 8: Góc \({C_4}\) kề bù với góc nào?
A. Góc\({D_4}.\)
B. Góc\({D_2}.\)
C. Góc\({C_2}.\)
D. Góc\({C_1}.\)
Câu 9: Góc \({D_1}\) đối đỉnh với góc nào?
A. Góc\({D_1}\).
B. Góc\({D_2}\).
C. Góc \({D_3}\).
D. Góc\({D_4}\).
Câu 10: Nếu \(a{\rm{//}}b\) thì số đo góc \({D_1}\) bằng số đo
A. góc \({C_1}\).
B. góc \({C_2}\).
C. góc \({C_4}\).
D. góc \({D_2}\).
Câu 11: Qua một điểm nằm ngoài một đường thẳng, có bao nhiêu đường thẳng song song với đường thẳng đó?
A. \(0.\)
B. \(1.\)
C. \(2.\)
D. Vô số.
Câu 12: Cho Hình 6, cần thêm điều kiện gì thì \(AB{\rm{//}}DC\)?
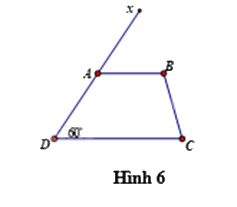
A. \(\widehat {BCD} = 60^\circ \)
B. \(\widehat {BCD} = 120^\circ \)
C. \(\widehat {BAD} = 60^\circ \)
D. \(\widehat {xAB} = 60^\circ \)
Phần tự luận (7 điểm)
Bài 1: (0,5 điểm) So sánh hai số hữu tỉ sau: \(0,25\) và \(\frac{1}{3}\)
Bài 2: (2,0 điểm) Thực hiện phép tính:
a) \(\left( { - 0,25} \right).40\; + 3\)
b) \(\frac{1}{7} \cdot \frac{{ - 3}}{8} + \frac{{ - 13}}{8} \cdot \frac{1}{7}\)
c) \(\left[ {\left( {\frac{2}{3} - \frac{1}{4}} \right) + {{\left( { - 2} \right)}^2}.3} \right] - 1\)
Bài 3: (2,0 điểm) Tìm x, biết:
a) \(x - 4 = \frac{1}{2}\)
b) \(2.\left( {x - 1} \right) = {3^3} - 1\)
Bài 4: (1,5 điểm)
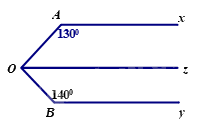
Hình 7
Cho Hình 7, biết \(Ax{\rm{//}}Oz\) và \(Ax{\rm{//}}By\).
a) Tính số đo góc \(AOz.\)
b) Chứng tỏ rằng góc \(AOB\) là góc vuông.
c) Tia \(Oz\) có là tia phân giác của góc \(AOB\) không? Vì sao?
Bài 5: (1,0 điểm)
Để nâng cao hiệu quả phòng chống dịch bệnh, học sinh phải thực hiện việc test nhanh Covid trước khi đến trường. Giá ban đầu để test mẫu gộp là \(40000\)đồng/1 học sinh, mẫu đơn là \(100000\)đồng/1 học sinh. Do lớp 7A test sau ngày 21/2/2022 nên được giảm giá 30%. Tính chi phí test nhanh Covid của lớp 7A biết có \(13\) em test mẫu gộp, \(22\) em test mẫu đơn.
-------- Hết --------
Phần trắc nghiệm (3 điểm)
Câu 1: D | Câu 2: C | Câu 3: B | Câu 4: A | Câu 5: A | Câu 6: B |
Câu 7. D | Câu 8. D | Câu 9. C | Câu 10. A | Câu 11. B | Câu 12. D |
Câu 1: Số đối của số hữu tỉ \( - 0,25\) là
A. \( - 0,25.\) | B. \(\frac{{ - 1}}{4}.\) |
C. \( - 4.\) | D. \(0,25.\) |
Phương pháp
Số đối của một số hữu tỉ a là – a.
Lời giải
Số đối của -0,25 là –(-0,25) = 0,25.
Đáp án D.
Câu 2: Trong các số sau, số nào là số hữu tỉ âm?
A. \(\frac{0}{{ - 2}}\) | B. \(\frac{{ - 2}}{{ - 1}}\) |
C. \( - \frac{1}{2}\) | D. \(\frac{{ - \left( { - 2} \right)}}{3}\) |
Phương pháp
Số hữu tỉ âm là số nhỏ hơn 0.
Lời giải
\(\frac{0}{{ - 2}} = 0\) nên không phải số hữu tỉ âm.
\(\frac{{ - 2}}{{ - 1}} = 2 > 0\) nên không phải số hữu tỉ âm.
\( - \frac{1}{2} < 0\) nên là số hữu tỉ âm.
\(\frac{{ - \left( { - 2} \right)}}{3} = \frac{2}{3} > 0\) nên không phải là số hữu tỉ âm.
Đáp án C.
Câu 3:Khi biểu diễu số hữu tỉ a và b trên trục số nằm ngang ta thấy điểm a nằm bên phải điểm b thì
A. \(a < b.\) | B. \(a > b.\) |
C. \(a = b.\) | D. \(a = - b.\) |
Phương pháp
Theo thứ tự trong tập hợp số hữu tỉ thì số nằm bên phải sẽ là số lớn hơn.
Lời giải
Vì điểm a nằm bên phải điểm b nên a > b.
Đáp án B.
Câu 4: Kết quả của phép tính \({7^{10}}:7\) viết dưới dạng lũy thừa là
A. \({7^9}.\) | B. \({7^{11}}.\) |
C. \({7^{10}}.\) | D. \({1^{10}}.\) |
Phương pháp
Sử dụng quy tắc chia hai lũy thừa cùng cơ số.
Lời giải
\({7^{10}}:7 = {7^{10 - 1}} = {7^9}\).
Đáp án A.
Câu 5: Với \(a,b,c\) là ba số hữu tỉ bất kì, nếu \(a - b = c\) thì
A. \(a = b + c.\) | B. \(a = - b + c.\) |
C. \(a = b - c.\) | D. \(a = - b - c.\) |
Phương pháp
Dựa vào quy tắc chuyển vế.
Lời giải
Nếu a – b = c thì a = b + c.
Đáp án A.
Câu 6: Với \(x,y,z\) là ba số hữu tỉ bất kì, sau khi bỏ ngoặc ta được \(x - \left( {y + z} \right)\) bằng
A. \(x - y + z.\) | B. \(x - y - z.\) |
C. \(x + y - z.\) | D. \(x + y + z.\) |
Phương pháp
Dựa vào quy tắc dấu ngoặc.
Lời giải
Ta có: x – (y + z) = x – y – z.
Đáp án B.
Câu 7: Trong các hình dưới đây, hình nào mô tả không đúng cách vẽ tia phân giác của một góc?
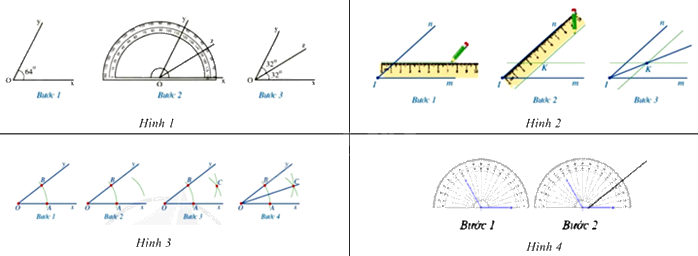
A. Hình 1. | B. Hình 2. |
C. Hình 3. | D. Hình 4. |
Phương pháp
Dựa vào cách vẽ tia phân giác đã học.
Lời giải
Trong các cách vẽ tia phân giác của một góc trên, chỉ có hình 4 chưa mô tả được đầy đủ cách để vẽ tia phân giác của một góc.
Đáp án D.
Sử dụng Hình 5 để trả lời các câu hỏi từ Câu 8 đến Câu 10.
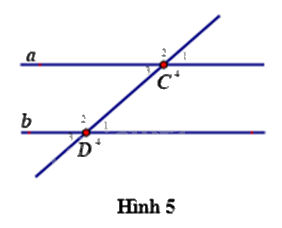
Câu 8: Góc \({C_4}\) kề bù với góc nào?
A. Góc \({D_4}.\) | B. Góc \({D_2}.\) |
C. Góc \({C_2}.\) | D. Góc \({C_1}.\) |
Phương pháp
Hai góc kề bù là hai góc kề nhau và có tổng bằng 1800.
Lời giải
Quan sát hình vẽ, ta thấy góc \({C_4}\) kề bù với góc \({C_3}\) và góc \({C_1}\) nên ta chọn đáp án D.
Đáp án D.
Câu 9: Góc \({D_1}\) đối đỉnh với góc nào?
A. Góc \({D_1}\). | B. Góc \({D_2}\). |
C. Góc \({D_3}\). | D. Góc \({D_4}\). |
Phương pháp
Dựa vào kiến thức hai góc đối đỉnh.
Lời giải
Quan sát hình vẽ, ta thấy góc \({D_1}\) đối đỉnh với góc \({D_3}\).
Đáp án C.
Câu 10: Nếu \(a{\rm{//}}b\) thì số đo góc \({D_1}\) bằng số đo
A. góc \({C_1}\). | B. góc \({C_2}\). |
C. góc \({C_4}\). | D. góc \({D_2}\). |
Phương pháp
Dựa vào kiến thức về hai đường thẳng song song.
Lời giải
Vì a // b nên \(\widehat {{C_1}} = \widehat {{D_1}}\)(hai góc đồng vị).
Đáp án A.
Câu 11: Qua một điểm nằm ngoài một đường thẳng, có bao nhiêu đường thẳng song song với đường thẳng đó?
A. \(0.\) | B. \(1.\) |
C. \(2.\) | D. Vô số. |
Phương pháp
Dựa vào kiến thức về hai đường thẳng song song.
Lời giải
Qua một điểm nằm ngoài một đường thẳng, chỉ có một đường thẳng song song với đường thẳng đó.
Đáp án B.
Câu 12: Cho Hình 6, cần thêm điều kiện gì thì \(AB{\rm{//}}DC\)?
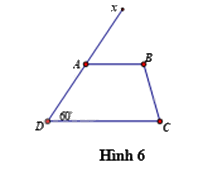
A. \(\widehat {BCD} = 60^\circ \) | B. \(\widehat {BCD} = 120^\circ \) |
C. \(\widehat {BAD} = 60^\circ \) | D. \(\widehat {xAB} = 60^\circ \) |
Phương pháp
Hai đường thẳng song song với nhau nếu hai góc đồng vị bằng nhau.
Lời giải
Để AB // DC thì \(\widehat {xAB} = \widehat {ADC}\) (hai góc đồng vị). Mà \(\widehat {ADC} = {60^0}\) nên để AB // DC thì \(\widehat {xAB} = 60^\circ \)
Đáp án D.
Phần tự luận.
Bài 1: (0,5 điểm) So sánh hai số hữu tỉ sau: \(0,25\) và \(\frac{1}{3}\).
Phương pháp
Viết hai phân số về dạng số hữu tỉ để so sánh.
Lời giải
Ta có: \(0,25 = \frac{1}{4}\).
Vì 4 > 3 nên \(\frac{1}{4} < \frac{1}{3}\).
Vậy \(0,25 < \frac{1}{3}\).
Bài 2: (2,0 điểm) Thực hiện phép tính:
a) \(\left( { - 0,25} \right).40\; + 3\) | b) \(\frac{1}{7} \cdot \frac{{ - 3}}{8} + \frac{{ - 13}}{8} \cdot \frac{1}{7}\) | c) \(\left[ {\left( {\frac{2}{3} - \frac{1}{4}} \right) + {{\left( { - 2} \right)}^2}.3} \right] - 1\) |
Phương pháp
Dựa vào quy tắc tính với số hữu tỉ để tính.
Lời giải
a) \(\left( { - 0,25} \right).40\; + 3\)
= -10 + 3
= -7
b) \(\frac{1}{7} \cdot \frac{{ - 3}}{8} + \frac{{ - 13}}{8} \cdot \frac{1}{7}\)
\(\begin{array}{l} = \frac{1}{7}\left( {\frac{{ - 3}}{8} + \frac{{ - 13}}{8}} \right)\\ = \frac{1}{7}\left( {\frac{{ - 3 - 13}}{8}} \right)\\ = \frac{1}{7}.\frac{{ - 16}}{8}\\ = \frac{1}{7}.\left( { - 2} \right)\\ = \frac{{ - 2}}{7}\end{array}\)
c) \(\left[ {\left( {\frac{2}{3} - \frac{1}{4}} \right) + {{\left( { - 2} \right)}^2}.3} \right] - 1\)
\( = {\rm{ }}\;\left[ {\frac{5}{{12}} + 12} \right] - 1\)
\( = {\rm{ }}\;\frac{{149}}{{12}} - 1\)
\( = {\rm{ }}\frac{{137}}{{12}}\)
Bài 3: (2,0 điểm) Tìm x, biết:
a) \(x - 4 = \frac{1}{2}\) | b) \(2.\left( {x - 1} \right) = {3^3} - 1\) |
Phương pháp
Sử dụng quy tắc chuyển vế để tìm x.
Lời giải
\({\rm{a) }}x - 4 = \frac{1}{2}\)
\({\rm{ }}x = \frac{1}{2} + 4\)
\({\rm{ }}x = \frac{9}{2}\)
Vậy \({\rm{ }}x = \frac{9}{2}\).
b) \(2.\left( {x - 1} \right) = {3^3} - 1\)
\(2.\left( {x - 1} \right) = 8\)
\(x - 1 = 4\)
\(\begin{array}{l}x = 4 + 1\\x = 5\end{array}\)
Vậy \(x = 5\).
Bài 4: (1,5 điểm)
Cho Hình 7, biết \(Ax{\rm{//}}Oz\) và \(Ax{\rm{//}}By\). a) Tính số đo góc \(AOz.\) |
Hình 7 |
b) Chứng tỏ rằng góc \(AOB\) là góc vuông. | |
c) Tia \(Oz\) có là tia phân giác của góc \(AOB\) không? Vì sao? |
Phương pháp
a) Góc xAO và góc AOz là hai góc trong cùng phía nên bù nhau.
b) Chứng minh \(\widehat {AOB} = \widehat {AOz} + \widehat {zOB} = {90^0}\).
c) Kiểm tra xem \(\widehat {{O_1}}\) và \(\widehat {{O_2}}\) có bằng nhau không.
Lời giải
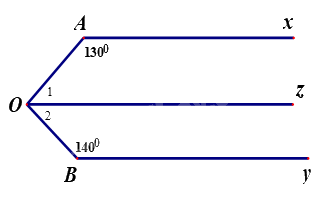
a) Vì \(Ax//Oz\) nên\(\widehat {AOz} + \widehat {OAx} = {180^0}\) (hai góc trong cùng phía bù nhau).
\( \Rightarrow \widehat {AOz} = {180^0} - \widehat {OAx} = {180^0} - {130^0} = {50^0}\)
b) Vì \(Ax//Oz\)và \(Ax//By\) nên \(Oz//By\).
\( \Rightarrow \widehat {{O_2}} + \widehat {OBy} = {180^0}\) (hai góc trong cùng phía bù nhau).
\( \Rightarrow \widehat {{O_2}} = {180^0} - \widehat {OBy} = {180^0} - {140^0} = {40^0}\)
Do đó: \(\widehat {AOB} = \widehat {{O_1}} + \widehat {{O_2}} = {50^0} + {40^0} = {90^0}\).
Vậy AOB là góc vuông.
c) Tia Oz không là tia phân giác của góc \(AOB\) vì: \(\widehat {{O_1}} = {50^0} \ne {40^0} = \widehat {{O_2}}\).
Bài 5: (1,0 điểm)
Để nâng cao hiệu quả phòng chống dịch bệnh, học sinh phải thực hiện việc test nhanh Covid trước khi đến trường. Giá ban đầu để test mẫu gộp là \(40000\)đồng/1 học sinh, mẫu đơn là \(100000\)đồng/1 học sinh. Do lớp 7A test sau ngày 21/2/2022 nên được giảm giá 30%. Tính chi phí test nhanh Covid của lớp 7A biết có \(13\) em test mẫu gộp, \(22\) em test mẫu đơn.
Phương pháp
Tính chi phí test Covid ban đầu.
Tính chi phí test Covid sau khi được giảm giá.
Lời giải
Chi phí test cô vít của lớp 7A khi chưa được giảm giá là:
\(13.40000 + 22.100000 = 2720000\)(đồng)
Chi phí test cô vít của lớp 7A sau khi được giảm giá là:
\(2720000.(100\% - 30\%) = 1904000\)(đồng)
Phần trắc nghiệm (3 điểm)
Câu 1: D | Câu 2: C | Câu 3: B | Câu 4: A | Câu 5: A | Câu 6: B |
Câu 7. D | Câu 8. D | Câu 9. C | Câu 10. A | Câu 11. B | Câu 12. D |
Câu 1: Số đối của số hữu tỉ \( - 0,25\) là
A. \( - 0,25.\) | B. \(\frac{{ - 1}}{4}.\) |
C. \( - 4.\) | D. \(0,25.\) |
Phương pháp
Số đối của một số hữu tỉ a là – a.
Lời giải
Số đối của -0,25 là –(-0,25) = 0,25.
Đáp án D.
Câu 2: Trong các số sau, số nào là số hữu tỉ âm?
A. \(\frac{0}{{ - 2}}\) | B. \(\frac{{ - 2}}{{ - 1}}\) |
C. \( - \frac{1}{2}\) | D. \(\frac{{ - \left( { - 2} \right)}}{3}\) |
Phương pháp
Số hữu tỉ âm là số nhỏ hơn 0.
Lời giải
\(\frac{0}{{ - 2}} = 0\) nên không phải số hữu tỉ âm.
\(\frac{{ - 2}}{{ - 1}} = 2 > 0\) nên không phải số hữu tỉ âm.
\( - \frac{1}{2} < 0\) nên là số hữu tỉ âm.
\(\frac{{ - \left( { - 2} \right)}}{3} = \frac{2}{3} > 0\) nên không phải là số hữu tỉ âm.
Đáp án C.
Câu 3:Khi biểu diễu số hữu tỉ a và b trên trục số nằm ngang ta thấy điểm a nằm bên phải điểm b thì
A. \(a < b.\) | B. \(a > b.\) |
C. \(a = b.\) | D. \(a = - b.\) |
Phương pháp
Theo thứ tự trong tập hợp số hữu tỉ thì số nằm bên phải sẽ là số lớn hơn.
Lời giải
Vì điểm a nằm bên phải điểm b nên a > b.
Đáp án B.
Câu 4: Kết quả của phép tính \({7^{10}}:7\) viết dưới dạng lũy thừa là
A. \({7^9}.\) | B. \({7^{11}}.\) |
C. \({7^{10}}.\) | D. \({1^{10}}.\) |
Phương pháp
Sử dụng quy tắc chia hai lũy thừa cùng cơ số.
Lời giải
\({7^{10}}:7 = {7^{10 - 1}} = {7^9}\).
Đáp án A.
Câu 5: Với \(a,b,c\) là ba số hữu tỉ bất kì, nếu \(a - b = c\) thì
A. \(a = b + c.\) | B. \(a = - b + c.\) |
C. \(a = b - c.\) | D. \(a = - b - c.\) |
Phương pháp
Dựa vào quy tắc chuyển vế.
Lời giải
Nếu a – b = c thì a = b + c.
Đáp án A.
Câu 6: Với \(x,y,z\) là ba số hữu tỉ bất kì, sau khi bỏ ngoặc ta được \(x - \left( {y + z} \right)\) bằng
A. \(x - y + z.\) | B. \(x - y - z.\) |
C. \(x + y - z.\) | D. \(x + y + z.\) |
Phương pháp
Dựa vào quy tắc dấu ngoặc.
Lời giải
Ta có: x – (y + z) = x – y – z.
Đáp án B.
Câu 7: Trong các hình dưới đây, hình nào mô tả không đúng cách vẽ tia phân giác của một góc?
A. Hình 1. | B. Hình 2. |
C. Hình 3. | D. Hình 4. |
Phương pháp
Dựa vào cách vẽ tia phân giác đã học.
Lời giải
Trong các cách vẽ tia phân giác của một góc trên, chỉ có hình 4 chưa mô tả được đầy đủ cách để vẽ tia phân giác của một góc.
Đáp án D.
Sử dụng Hình 5 để trả lời các câu hỏi từ Câu 8 đến Câu 10.
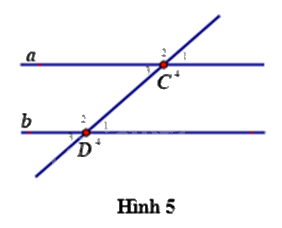
Câu 8: Góc \({C_4}\) kề bù với góc nào?
A. Góc \({D_4}.\) | B. Góc \({D_2}.\) |
C. Góc \({C_2}.\) | D. Góc \({C_1}.\) |
Phương pháp
Hai góc kề bù là hai góc kề nhau và có tổng bằng 1800.
Lời giải
Quan sát hình vẽ, ta thấy góc \({C_4}\) kề bù với góc \({C_3}\) và góc \({C_1}\) nên ta chọn đáp án D.
Đáp án D.
Câu 9: Góc \({D_1}\) đối đỉnh với góc nào?
A. Góc \({D_1}\). | B. Góc \({D_2}\). |
C. Góc \({D_3}\). | D. Góc \({D_4}\). |
Phương pháp
Dựa vào kiến thức hai góc đối đỉnh.
Lời giải
Quan sát hình vẽ, ta thấy góc \({D_1}\) đối đỉnh với góc \({D_3}\).
Đáp án C.
Câu 10: Nếu \(a{\rm{//}}b\) thì số đo góc \({D_1}\) bằng số đo
A. góc \({C_1}\). | B. góc \({C_2}\). |
C. góc \({C_4}\). | D. góc \({D_2}\). |
Phương pháp
Dựa vào kiến thức về hai đường thẳng song song.
Lời giải
Vì a // b nên \(\widehat {{C_1}} = \widehat {{D_1}}\)(hai góc đồng vị).
Đáp án A.
Câu 11: Qua một điểm nằm ngoài một đường thẳng, có bao nhiêu đường thẳng song song với đường thẳng đó?
A. \(0.\) | B. \(1.\) |
C. \(2.\) | D. Vô số. |
Phương pháp
Dựa vào kiến thức về hai đường thẳng song song.
Lời giải
Qua một điểm nằm ngoài một đường thẳng, chỉ có một đường thẳng song song với đường thẳng đó.
Đáp án B.
Câu 12: Cho Hình 6, cần thêm điều kiện gì thì \(AB{\rm{//}}DC\)?
A. \(\widehat {BCD} = 60^\circ \) | B. \(\widehat {BCD} = 120^\circ \) |
C. \(\widehat {BAD} = 60^\circ \) | D. \(\widehat {xAB} = 60^\circ \) |
Phương pháp
Hai đường thẳng song song với nhau nếu hai góc đồng vị bằng nhau.
Lời giải
Để AB // DC thì \(\widehat {xAB} = \widehat {ADC}\) (hai góc đồng vị). Mà \(\widehat {ADC} = {60^0}\) nên để AB // DC thì \(\widehat {xAB} = 60^\circ \)
Đáp án D.
Phần tự luận.
Bài 1: (0,5 điểm) So sánh hai số hữu tỉ sau: \(0,25\) và \(\frac{1}{3}\).
Phương pháp
Viết hai phân số về dạng số hữu tỉ để so sánh.
Lời giải
Ta có: \(0,25 = \frac{1}{4}\).
Vì 4 > 3 nên \(\frac{1}{4} < \frac{1}{3}\).
Vậy \(0,25 < \frac{1}{3}\).
Bài 2: (2,0 điểm) Thực hiện phép tính:
a) \(\left( { - 0,25} \right).40\; + 3\) | b) \(\frac{1}{7} \cdot \frac{{ - 3}}{8} + \frac{{ - 13}}{8} \cdot \frac{1}{7}\) | c) \(\left[ {\left( {\frac{2}{3} - \frac{1}{4}} \right) + {{\left( { - 2} \right)}^2}.3} \right] - 1\) |
Phương pháp
Dựa vào quy tắc tính với số hữu tỉ để tính.
Lời giải
a) \(\left( { - 0,25} \right).40\; + 3\)
= -10 + 3
= -7
b) \(\frac{1}{7} \cdot \frac{{ - 3}}{8} + \frac{{ - 13}}{8} \cdot \frac{1}{7}\)
\(\begin{array}{l} = \frac{1}{7}\left( {\frac{{ - 3}}{8} + \frac{{ - 13}}{8}} \right)\\ = \frac{1}{7}\left( {\frac{{ - 3 - 13}}{8}} \right)\\ = \frac{1}{7}.\frac{{ - 16}}{8}\\ = \frac{1}{7}.\left( { - 2} \right)\\ = \frac{{ - 2}}{7}\end{array}\)
c) \(\left[ {\left( {\frac{2}{3} - \frac{1}{4}} \right) + {{\left( { - 2} \right)}^2}.3} \right] - 1\)
\( = {\rm{ }}\;\left[ {\frac{5}{{12}} + 12} \right] - 1\)
\( = {\rm{ }}\;\frac{{149}}{{12}} - 1\)
\( = {\rm{ }}\frac{{137}}{{12}}\)
Bài 3: (2,0 điểm) Tìm x, biết:
a) \(x - 4 = \frac{1}{2}\) | b) \(2.\left( {x - 1} \right) = {3^3} - 1\) |
Phương pháp
Sử dụng quy tắc chuyển vế để tìm x.
Lời giải
\({\rm{a) }}x - 4 = \frac{1}{2}\)
\({\rm{ }}x = \frac{1}{2} + 4\)
\({\rm{ }}x = \frac{9}{2}\)
Vậy \({\rm{ }}x = \frac{9}{2}\).
b) \(2.\left( {x - 1} \right) = {3^3} - 1\)
\(2.\left( {x - 1} \right) = 8\)
\(x - 1 = 4\)
\(\begin{array}{l}x = 4 + 1\\x = 5\end{array}\)
Vậy \(x = 5\).
Bài 4: (1,5 điểm)
Cho Hình 7, biết \(Ax{\rm{//}}Oz\) và \(Ax{\rm{//}}By\). a) Tính số đo góc \(AOz.\) |
Hình 7 |
b) Chứng tỏ rằng góc \(AOB\) là góc vuông. | |
c) Tia \(Oz\) có là tia phân giác của góc \(AOB\) không? Vì sao? |
Phương pháp
a) Góc xAO và góc AOz là hai góc trong cùng phía nên bù nhau.
b) Chứng minh \(\widehat {AOB} = \widehat {AOz} + \widehat {zOB} = {90^0}\).
c) Kiểm tra xem \(\widehat {{O_1}}\) và \(\widehat {{O_2}}\) có bằng nhau không.
Lời giải
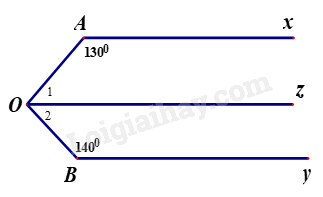
a) Vì \(Ax//Oz\) nên\(\widehat {AOz} + \widehat {OAx} = {180^0}\) (hai góc trong cùng phía bù nhau).
\( \Rightarrow \widehat {AOz} = {180^0} - \widehat {OAx} = {180^0} - {130^0} = {50^0}\)
b) Vì \(Ax//Oz\)và \(Ax//By\) nên \(Oz//By\).
\( \Rightarrow \widehat {{O_2}} + \widehat {OBy} = {180^0}\) (hai góc trong cùng phía bù nhau).
\( \Rightarrow \widehat {{O_2}} = {180^0} - \widehat {OBy} = {180^0} - {140^0} = {40^0}\)
Do đó: \(\widehat {AOB} = \widehat {{O_1}} + \widehat {{O_2}} = {50^0} + {40^0} = {90^0}\).
Vậy AOB là góc vuông.
c) Tia Oz không là tia phân giác của góc \(AOB\) vì: \(\widehat {{O_1}} = {50^0} \ne {40^0} = \widehat {{O_2}}\).
Bài 5: (1,0 điểm)
Để nâng cao hiệu quả phòng chống dịch bệnh, học sinh phải thực hiện việc test nhanh Covid trước khi đến trường. Giá ban đầu để test mẫu gộp là \(40000\)đồng/1 học sinh, mẫu đơn là \(100000\)đồng/1 học sinh. Do lớp 7A test sau ngày 21/2/2022 nên được giảm giá 30%. Tính chi phí test nhanh Covid của lớp 7A biết có \(13\) em test mẫu gộp, \(22\) em test mẫu đơn.
Phương pháp
Tính chi phí test Covid ban đầu.
Tính chi phí test Covid sau khi được giảm giá.
Lời giải
Chi phí test cô vít của lớp 7A khi chưa được giảm giá là:
\(13.40000 + 22.100000 = 2720000\)(đồng)
Chi phí test cô vít của lớp 7A sau khi được giảm giá là:
\(2720000.(100\% - 30\%) = 1904000\)(đồng)
Đề thi giữa kì 1 Toán 7 - Đề số 9 chương trình Kết nối tri thức là một bài kiểm tra quan trọng giúp học sinh đánh giá mức độ nắm vững kiến thức đã học trong giai đoạn đầu năm học lớp 7. Đề thi bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính như số hữu tỉ, số thực, biểu thức đại số, phương trình bậc nhất một ẩn, và các ứng dụng thực tế của toán học.
Thông thường, đề thi giữa kì 1 Toán 7 - Đề số 9 theo chương trình Kết nối tri thức sẽ có cấu trúc như sau:
Các bài tập về số hữu tỉ và số thực thường yêu cầu học sinh:
Các bài tập về biểu thức đại số thường yêu cầu học sinh:
Các bài tập về phương trình bậc nhất một ẩn thường yêu cầu học sinh:
Bài tập 1: Tính giá trị của biểu thức A = 2x + 3y khi x = -1 và y = 2.
Giải: Thay x = -1 và y = 2 vào biểu thức A, ta có:
A = 2(-1) + 3(2) = -2 + 6 = 4
Bài tập 2: Giải phương trình 3x - 5 = 7.
Giải:
Giaitoan.edu.vn cung cấp đầy đủ các tài liệu học tập, đề thi thử, và bài giải chi tiết cho các môn học, đặc biệt là môn Toán. Chúng tôi luôn cập nhật những thông tin mới nhất và hữu ích nhất để giúp các em học sinh học tập hiệu quả và đạt kết quả tốt nhất.