Chào mừng các em học sinh lớp 7 đến với đề thi giữa kì 1 Toán 7 Kết nối tri thức - Đề số 13. Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong giai đoạn đầu của năm học.
Giaitoan.edu.vn cung cấp đề thi với cấu trúc bám sát chương trình học, giúp các em làm quen với dạng đề và rèn luyện kỹ năng giải toán.
Khẳng định nào sau đây sai?
\( - 5 \in \mathbb{Q}\).
\(\frac{{ - 3}}{5} \notin \mathbb{Z}\).
\(6,7 \in \mathbb{N}\).
\(\frac{3}{4} \in \mathbb{Q}\).
Số đối của \( - \frac{1}{2}\) là
\( - \frac{1}{2}\) .
-1.
1.
\(\frac{1}{2}\).
Số 125 viết được dưới dạng luỹ thừa của 5 là
5125.
-5125.
-53.
53.
Viết số \({\left( {\frac{1}{9}} \right)^4}\) dưới dạng luỹ thừa cơ số \(\frac{1}{3}\) ta được
\({\left( {\frac{1}{3}} \right)^4}\).
\({\left( {\frac{1}{3}} \right)^8}\).
\({\left( {\frac{1}{3}} \right)^6}\).
\({\left( {\frac{1}{3}} \right)^{12}}\).
Cho \(x \in \mathbb{Q},x \ne 0\) và \({x^3}.{x^2}\) bằng:
\({x^6}\).
\({x^7}:{x^2}\).
\({x^3} + {x^2}\).
\({\left( {{x^3}} \right)^2}\).
Kết quả của phép tính \(\sqrt {16} .\sqrt 4 - \sqrt {25} + 2\sqrt {49} \) là
15.
17.
-17.
16.
Cho hai góc kề bù \(\widehat {xOy}\) và \(\widehat {yOz}\), biết \(\widehat {yOz} = 100^\circ \). Khi đó số đo \(\widehat {xOy}\) là
\(100^\circ \).
\(80^\circ \).
\(10^\circ \).
\(110^\circ \).
Cho \(\widehat {xOy} = 70^\circ \), tia \(Oz\) là tia phân giác của \(\widehat {xOy}\). Số đo của \(\widehat {xOz}\) là:
\(30^\circ \).
\(140^\circ \).
\(60^\circ \).
\(35^\circ \).
Cho \(\widehat {xOy} = 60^\circ \). Nêu cách dựng tia phân giác Oz của góc xOy. Hãy sắp xếp một cách hợp lý các câu sau đây để có lời giải của bài toán trên.
1. Viết ký hiệu \(\widehat {xOz} = \widehat {zOy}\).
2. Vẽ tia Oz nằm giữa hai tia Ox và Oy sao cho \(\widehat {xOz} = 30^\circ \).
3. Vẽ \(\widehat {xOy} = 60^\circ \) .
Sắp xếp nào sau đây là đúng?
3, 2, 1.
1, 2, 3.
3, 1, 2.
2, 3, 1.
Khẳng định đúng là:
Hai góc đối đỉnh thì bằng nhau.
Hai góc bằng nhau thì đối đỉnh.
Hai góc đối đỉnh thì bù nhau.
Hai góc có đỉnh trùng nhau là hai góc đối đỉnh.
Cho hình vẽ bên. Biết a//b, \(\widehat {{M_1}} = {85^o}\), khi đó \(\widehat {{N_1}} = ?\)
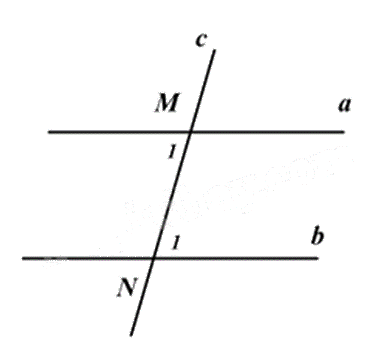
\({85^0}\).
\({95^0}\).
\({100^0}\).
\({105^0}\).
Trong các khẳng định sau, khẳng định nào cho ta một định lí?
Hai góc so le trong thì bằng nhau.
Hai góc bằng nhau thì so le trong.
Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì chúng vuông góc với nhau.
Thực hiện phép tính:
a) \(\frac{{23}}{7} + \frac{4}{3} - \frac{9}{7} + \frac{{10}}{6}\);
b) \(\left( {\frac{5}{8} - \frac{{\sqrt 9 }}{{12}}} \right):\frac{3}{4} + \frac{{11}}{8}:\frac{3}{4}\);
c) \(\left( {0,\left( 3 \right) + \frac{{\left| { - 2} \right|}}{3}} \right):\frac{{\sqrt {25} }}{4} - {\left( {{2^3} + {3^2}} \right)^0}\).
Tìm \(x\), biết:
a) \(\frac{2}{3} - \frac{5}{2}x = \frac{{ - 13}}{3}\);
b) \(2.\left| {3 - 2x} \right| + \frac{1}{2} = \frac{5}{2}\);
c) \({x^2}.({2^x} - 6) - 2{x^2} = 0\).
Một ngày cửa hàng bánh mì nhập \(200\) chiếc bánh mì để bán. Buổi sáng, cửa hàng bán được \(\frac{3}{5}\) số bánh mì với giá \(15\,000\)đồng một cái.
a) Số tiền buổi sáng cửa hàng bánh mì thu được là bao nhiêu?
b) Buổi chiều, để bán nốt số bánh mì còn lại cửa hàng giảm giá 20% so với giá bán buổi sáng. Tính tổng số tiền bán bánh mì của cửa hàng thu được trong một ngày nếu bán hết bánh mì.
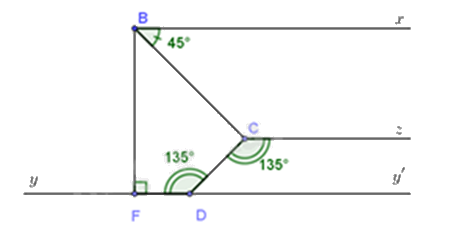
Cho hình vẽ bên, biết \(\widehat {FDC} = 135^\circ ,\widehat {CBx} = 45^\circ ,\)\(\widehat {DCz} = 135^\circ \), \(Dy\parallel Bx,Dy \bot BF\) tại điểm \(F\).
a) Vẽ hình và chứng minh \(Cz\parallel Dy\).
b) Chứng minh \(BC\) là tia phân giác của \(\widehat {FBx}\).
c) Kẻ tia \(Ct\) là tia phân giác của \(\widehat {BCD}\). Chứng minh \(Ct\parallel Dy\).
Tìm \(x,y,z\) biết: \(\sqrt {{{(x - 2024)}^2}} + \left| {x + y - 4z} \right| + {y^2}.\sqrt 5 = 0\) với \(x,y,z \in \mathbb{R}\).
Khẳng định nào sau đây sai?
\( - 5 \in \mathbb{Q}\).
\(\frac{{ - 3}}{5} \notin \mathbb{Z}\).
\(6,7 \in \mathbb{N}\).
\(\frac{3}{4} \in \mathbb{Q}\).
Đáp án : C
Dựa vào kiến thức về các tập hợp \(\mathbb{N},\mathbb{Z},\mathbb{R},\mathbb{Q}\).
\( - 5 = \frac{{ - 5}}{1}\) là số hữu tỉ nên \( - 5 \in \mathbb{Q}\) là khẳng định đúng.
\(\frac{{ - 3}}{5}\) không phải số nguyên nên \(\frac{{ - 3}}{5} \notin \mathbb{Z}\) là khẳng định đúng.
\(6,7\) không phải số tự nhiên nên khẳng định \(6,7 \in \mathbb{N}\) là khẳng định sai.
\(\frac{3}{4}\) là số hữu tỉ nên \(\frac{3}{4} \in \mathbb{Q}\) là khẳng định đúng.
Đáp án C.
Số đối của \( - \frac{1}{2}\) là
\( - \frac{1}{2}\) .
-1.
1.
\(\frac{1}{2}\).
Đáp án : D
Số đối của số hữu tỉ a là – a.
Số đối của \( - \frac{1}{2}\) là: \( - \left( { - \frac{1}{2}} \right) = \frac{1}{2}\).
Đáp án D.
Số 125 viết được dưới dạng luỹ thừa của 5 là
5125.
-5125.
-53.
53.
Đáp án : D
Biểu diễn 125 thành lũy thừa của 5.
Ta có: \(125 = 5.5.5 = {5^3}\).
Đáp án D.
Viết số \({\left( {\frac{1}{9}} \right)^4}\) dưới dạng luỹ thừa cơ số \(\frac{1}{3}\) ta được
\({\left( {\frac{1}{3}} \right)^4}\).
\({\left( {\frac{1}{3}} \right)^8}\).
\({\left( {\frac{1}{3}} \right)^6}\).
\({\left( {\frac{1}{3}} \right)^{12}}\).
Đáp án : B
Dựa vào kiến thức lũy thừa của lũy thừa: \({\left( {{x^m}} \right)^n} = {x^{m.n}}\).
Ta có: \({\left( {\frac{1}{9}} \right)^4} = {\left[ {{{\left( {\frac{1}{3}} \right)}^2}} \right]^4} = {\left( {\frac{1}{3}} \right)^{2.4}} = {\left( {\frac{1}{3}} \right)^8}\).
Đáp án B.
Cho \(x \in \mathbb{Q},x \ne 0\) và \({x^3}.{x^2}\) bằng:
\({x^6}\).
\({x^7}:{x^2}\).
\({x^3} + {x^2}\).
\({\left( {{x^3}} \right)^2}\).
Đáp án : B
Dựa vào kiến thức:
\(\begin{array}{l}{x^m}.{x^n} = {x^{m + n}}\\{x^m}:{x^n} = {x^{m - n}}\left( {x \ne 0;m \ge n} \right)\end{array}\)
\({\left( {{x^m}} \right)^n} = {x^{m.n}}\)
Ta có: \({x^3}.{x^2} = {x^{3 + 2}} = {x^5}\).
\({x^7}:{x^2} = {x^{7 - 2}} = {x^5}\).
\({\left( {{x^3}} \right)^2} = {x^{3.2}} = {x^6}\).
Do đó \({x^3}.{x^2} = {x^7}:{x^2}\).
Đáp án B.
Kết quả của phép tính \(\sqrt {16} .\sqrt 4 - \sqrt {25} + 2\sqrt {49} \) là
15.
17.
-17.
16.
Đáp án : B
Sử dụng kiến thức về căn bậc hai và thực hiện phép tính.
Ta có:
\(\begin{array}{l}\sqrt {16} .\sqrt 4 - \sqrt {25} + 2\sqrt {49} \\ = 4.2 - 5 + 2.7\\ = 8 - 5 + 14\\ = 17\end{array}\)
Đáp án B.
Cho hai góc kề bù \(\widehat {xOy}\) và \(\widehat {yOz}\), biết \(\widehat {yOz} = 100^\circ \). Khi đó số đo \(\widehat {xOy}\) là
\(100^\circ \).
\(80^\circ \).
\(10^\circ \).
\(110^\circ \).
Đáp án : B
Sử dụng kiến thức về hai góc kề bù: tổng hai góc kề bù bằng \(180^\circ \).
Vì \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù nên \(\widehat {xOy} + \widehat {yOz} = 180^\circ \).
Suy ra \(\widehat {xOy} = 180^\circ - \widehat {yOz} = 180^\circ - 100^\circ = 80^\circ \).
Đáp án B.
Cho \(\widehat {xOy} = 70^\circ \), tia \(Oz\) là tia phân giác của \(\widehat {xOy}\). Số đo của \(\widehat {xOz}\) là:
\(30^\circ \).
\(140^\circ \).
\(60^\circ \).
\(35^\circ \).
Đáp án : D
Khi Oz là tia phân giác của góc xOy thì \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}\widehat {xOy}\).
Vì tia \(Oz\) là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}\widehat {xOy}\)
Suy ra \(\widehat {xOz} = \frac{1}{2}\widehat {xOy} = \frac{1}{2}.70^\circ = 35^\circ \).
Đáp án D.
Cho \(\widehat {xOy} = 60^\circ \). Nêu cách dựng tia phân giác Oz của góc xOy. Hãy sắp xếp một cách hợp lý các câu sau đây để có lời giải của bài toán trên.
1. Viết ký hiệu \(\widehat {xOz} = \widehat {zOy}\).
2. Vẽ tia Oz nằm giữa hai tia Ox và Oy sao cho \(\widehat {xOz} = 30^\circ \).
3. Vẽ \(\widehat {xOy} = 60^\circ \) .
Sắp xếp nào sau đây là đúng?
3, 2, 1.
1, 2, 3.
3, 1, 2.
2, 3, 1.
Đáp án : A
Dựa vào cách dựng tia phân giác của một góc.
Thứ tự sắp xếp đúng là: 3 – 2 – 1.
3. Vẽ \(\widehat {xOy} = 60^\circ \) .
2. Vẽ tia Oz nằm giữa hai tia Ox và Oy sao cho \(\widehat {xOz} = 30^\circ \).
1. Viết ký hiệu \(\widehat {xOz} = \widehat {zOy}\).
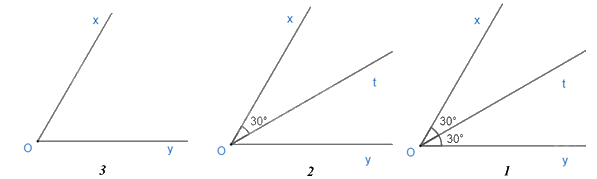
Đáp án A.
Khẳng định đúng là:
Hai góc đối đỉnh thì bằng nhau.
Hai góc bằng nhau thì đối đỉnh.
Hai góc đối đỉnh thì bù nhau.
Hai góc có đỉnh trùng nhau là hai góc đối đỉnh.
Đáp án : A
Dựa vào tính chất của hai góc đối đỉnh.
Hai góc đối đỉnh thì bằng nhau nên đáp án A đúng.
Đáp án A.
Cho hình vẽ bên. Biết a//b, \(\widehat {{M_1}} = {85^o}\), khi đó \(\widehat {{N_1}} = ?\)
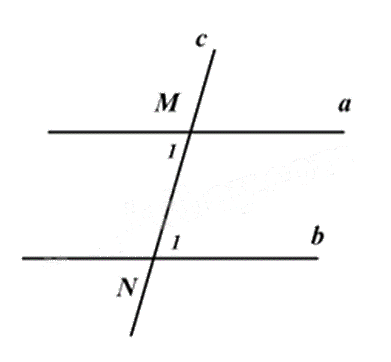
\({85^0}\).
\({95^0}\).
\({100^0}\).
\({105^0}\).
Đáp án : A
Dựa vào tính chất của hai đường thẳng song song (hai góc so le trong bằng nhau).
Vì a // b nên \(\widehat {{M_1}} = \widehat {{N_1}} = 85^\circ \) (hai góc so le trong)
Đáp án A.
Trong các khẳng định sau, khẳng định nào cho ta một định lí?
Hai góc so le trong thì bằng nhau.
Hai góc bằng nhau thì so le trong.
Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì chúng vuông góc với nhau.
Đáp án : C
Định lí là một khẳng định được suy ra từ những khẳng định đúng đã biết.
Dựa vào kiến thức về tính chất hai góc so le trong, hai đường thẳng song song.
Chỉ có hai góc so le trong của hai đường thẳng song song mới bằng nhau nên A không phải định lí.
Hai góc bằng nhau chưa chắc đã là hai góc so le trong nên B không phải định lí.
Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau nên C là định lí, D không phải định lí.
Đáp án C.
Thực hiện phép tính:
a) \(\frac{{23}}{7} + \frac{4}{3} - \frac{9}{7} + \frac{{10}}{6}\);
b) \(\left( {\frac{5}{8} - \frac{{\sqrt 9 }}{{12}}} \right):\frac{3}{4} + \frac{{11}}{8}:\frac{3}{4}\);
c) \(\left( {0,\left( 3 \right) + \frac{{\left| { - 2} \right|}}{3}} \right):\frac{{\sqrt {25} }}{4} - {\left( {{2^3} + {3^2}} \right)^0}\).
Dựa vào các quy tắc thực hiện phép tính với số thực, lũy thừa và thứ tự thực hiện phép tính.
a) \(\frac{{23}}{7} + \frac{4}{3} - \frac{9}{7} + \frac{{10}}{6}\)\( = \left( {\frac{{23}}{7} - \frac{9}{7}} \right) + \left( {\frac{4}{3} + \frac{5}{3}} \right)\)\( = 5\)
b) \(\left( {\frac{5}{8} - \frac{{\sqrt 9 }}{{12}}} \right):\frac{3}{4} + \frac{{11}}{8}:\frac{3}{4}\)\( = \left( {\frac{5}{8} - \frac{1}{4} + \frac{{11}}{8}} \right).\frac{4}{3}\)\( = \frac{7}{3}\)
c) \(\left( {0,\left( 3 \right) + \frac{{\left| { - 2} \right|}}{3}} \right):\frac{{\sqrt {25} }}{4} - {\left( {{2^3} + {3^2}} \right)^0}\)\( = \left( {\frac{1}{3} + \frac{2}{3}} \right).\frac{4}{5} - 1\)\( = \frac{{ - 1}}{5}\)
Tìm \(x\), biết:
a) \(\frac{2}{3} - \frac{5}{2}x = \frac{{ - 13}}{3}\);
b) \(2.\left| {3 - 2x} \right| + \frac{1}{2} = \frac{5}{2}\);
c) \({x^2}.({2^x} - 6) - 2{x^2} = 0\).
a) Sử dụng quy tắc chuyển vế.
b) Chuyển vế, sử dụng kiến thức \(\left| A \right| = k > 0\) thì xảy ra hai trường hợp: \(A = k\) hoặc \(A = - k\).
c) Sử dụng tính chất phân phối của phép nhân với phép cộng.
Khi A.B = 0 thì A = 0 hoặc B = 0.
a) \(\frac{2}{3} - \frac{5}{2}x = \frac{{ - 13}}{3}\)
\(\begin{array}{l}\frac{5}{2}x = \frac{2}{3} + \frac{{13}}{3}\\x = 2\end{array}\)
Vậy \(x = 2\).
b) \(2\left| {3 - 2x} \right| + \frac{1}{2} = \frac{5}{2}\)
\(\left| {3 - 2x} \right| = 1\)
TH1: \(3 - 2x = 1\)
\(\begin{array}{l}2x = 3 - 1\\2x = 2\\x = 2:2\\x = 1\end{array}\)
TH2: \(3 - 2x = - 1\)
\(\begin{array}{l}2x = 3 - \left( { - 1} \right)\\2x = 4\\x = 4:2\\x = 2\end{array}\)
Vậy \(x = 1;x = 2\).
c) \({x^2}.({2^x} - 6) - 2{x^2} = 0\)
\(\begin{array}{l}{x^2}.\left( {{2^x} - 6 - 2} \right) = 0\\{x^2}.\left( {{2^x} - 8} \right) = 0\end{array}\)
TH1: \({x^2} = 0\)
\(x = 0\)
TH2: \({2^x} - 8 = 0\)
\(\begin{array}{l}{2^x} = 8\\{2^x} = {2^3}\\x = 3\end{array}\)
Vậy \(x = 0;x = 3\).
Một ngày cửa hàng bánh mì nhập \(200\) chiếc bánh mì để bán. Buổi sáng, cửa hàng bán được \(\frac{3}{5}\) số bánh mì với giá \(15\,000\)đồng một cái.
a) Số tiền buổi sáng cửa hàng bánh mì thu được là bao nhiêu?
b) Buổi chiều, để bán nốt số bánh mì còn lại cửa hàng giảm giá 20% so với giá bán buổi sáng. Tính tổng số tiền bán bánh mì của cửa hàng thu được trong một ngày nếu bán hết bánh mì.
a) Tính số bánh mì buổi sáng bán được = \(\frac{3}{5}\) . tổng số bánh.
Tính số tiền buổi sáng bán được = giá một chiếc . số bánh bán được.
b) Tính giá bánh mì sau khi giảm 20% = giá một chiếc . (100% - 20%).
Tính số bánh mì còn lại sau buổi sáng = tổng số bánh – số bánh đã bán.
Tính số tiền bán được vào buổi chiều = số bánh còn lại . giá sau khi giảm.
Tính tổng số tiền bán bánh mì.
a) Buổi sáng bán được số bánh mì là:
\(200.\frac{3}{5} = 120\)(bánh mì)
Số tiền buổi sáng cửa hàng bánh mì thu được là:
\(15\,000.120 = 1\,800\,000\)(đồng)
b) Giá bán bánh mì sau khi giảm \(20\% \) là:
\(15\,000.\left( {100\% - 20\% } \right) = 12\,000\)(đồng)
Số bánh mì còn lại sau buổi sáng là:
\(200 - 120 = 80\)(bánh mì)
Số tiền thu được khi bán nốt bánh mì còn lại sau buổi sáng là:
\(12\,000.80 = 960\,000\) (đồng)
Tổng số tiền bán bánh mì của cửa hàng thu được trong một ngày là:
\(1\,800\,000 + 960\,000 = 2\,760\,000\) (đồng)
Vậy tổng số tiền bán bánh mì của cửa hàng thu được trong một ngày là 2 760 000 đồng.
Cho hình vẽ bên, biết \(\widehat {FDC} = 135^\circ ,\widehat {CBx} = 45^\circ ,\)\(\widehat {DCz} = 135^\circ \), \(Dy\parallel Bx,Dy \bot BF\) tại điểm \(F\).
a) Vẽ hình và chứng minh \(Cz\parallel Dy\).
b) Chứng minh \(BC\) là tia phân giác của \(\widehat {FBx}\).
c) Kẻ tia \(Ct\) là tia phân giác của \(\widehat {BCD}\). Chứng minh \(Ct\parallel Dy\).
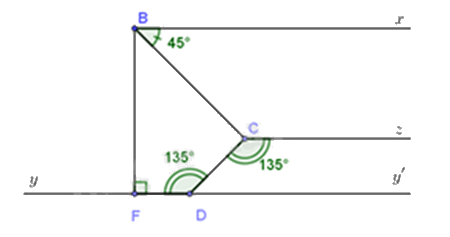
a) Sử dụng dấu hiệu nhận biết hai đường thẳng song song (hai góc so le trong bằng nhau)
b) Chứng minh \(\widehat {FBx} = 90^\circ \).
Chứng minh BC chia góc \(\widehat {FBx}\) thành hai góc bằng nhau.
c) Kéo dài Oz về phía O, ta được đường thẳng zz’ đi qua O.
Tính được \(\widehat {BCD} = 90^\circ \).
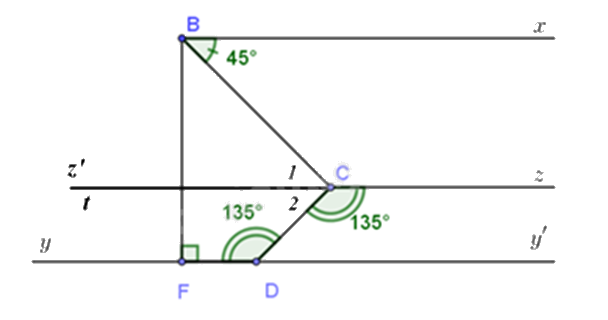
a) Vẽ lại hình
Vì \(\widehat {FDC} = \widehat {DCz} = 135^\circ \) mà \(\widehat {FDC}\) và \(\widehat {DCz}\) ở vị trí so le trong nên \(Cz\parallel Dy\) (dấu hiệu nhận biết)
b) Ta có, \(Dy//Bx;By \bot Dy\) suy ra \(BF \bot Bx\) (tính chất)
Suy ra \(\widehat {FBx} = 90^\circ \)
Tia \(BC\) nằm trong \(\widehat {FBx}\)
Mà \(\widehat {CBx} = \frac{1}{2}\widehat {FBx} = 45^\circ \)
Suy ra\(BC\) là tia phân giác của \(\widehat {FBx}\).
c) Kéo dài Oz về phía O, ta được đường thẳng zz’ đi qua O.
Khi đó \(Bx//zz'//yy'\)
Suy ra \(\widehat {xBC} = \widehat {{C_1}};\widehat {{C_2}} = \widehat {CDy'}\) (1).
Vì \(\widehat {yDC} + \widehat {CDy'} = 180^\circ \) (hai góc kề bù) nên \(\widehat {CDy'} = 180^\circ - \widehat {yDC} = 180^\circ - 135^\circ = 45^\circ \) (2).
Từ (1) và (2) suy ra \(\widehat {{C_1}} = 45^\circ ;\widehat {{C_2}} = 45^\circ \)
Do đó \(\widehat {BCD} = \widehat {{C_1}} + \widehat {{C_2}} = 45^\circ + 45^\circ = 90^\circ \) \(\)
Vì \(Ct\) là tia phân giác của \(\widehat {BCD}\) nên \(\widehat {DCt} = \frac{1}{2}\widehat {BCD} = 45^\circ \) (tính chất)
Suy ra \(\widehat {DCt} = \widehat {CDy'} = 45^\circ \).
Mà \(\widehat {DCt}\) và \(\widehat {CDy'}\) là hai góc so le trong.
Do đó \(Ct\parallel Dy\) (dấu hiệu nhận biết)
Tìm \(x,y,z\) biết: \(\sqrt {{{(x - 2024)}^2}} + \left| {x + y - 4z} \right| + {y^2}.\sqrt 5 = 0\) với \(x,y,z \in \mathbb{R}\).
Dựa vào tính chất của giá trị tuyệt đối, bình phương của một số.
Vì \({y^2} \ge 0\) với mọi \(y \in \mathbb{R}\) và \(\sqrt 5 > 0\) nên \({y^2}.\sqrt 5 \ge 0\) với mọi \(y \in \mathbb{R}\) .
Ta có: \(\sqrt {{{(x - 2024)}^2}} = \left| {x - 2024} \right| \ge 0\) với mọi \(x \in \mathbb{R}\);
\(\left| {x + y - 4z} \right| \ge 0\) với mọi \(x,y,z \in \mathbb{R}\) và \({y^2}.\sqrt 5 \ge 0\) với mọi \(y \in \mathbb{R}\)
nên \(\sqrt {{{(x - 2024)}^2}} + \left| {x + y - 4z} \right| + {y^2}.\sqrt 5 \ge 0\) với mọi \(x,y,z \in \mathbb{R}\).
Theo đề bài, ta có \(\sqrt {{{(x - 2024)}^2}} + \left| {x + y - 4z} \right| + {y^2}.\sqrt 5 = 0\) hay \(\left| {x - 2024} \right| + \left| {x + y - 4z} \right| + {y^2}.\sqrt 5 = 0\).
Giá trị của biểu thức bằng 0 khi
\(\begin{array}{l}\left| {x - 2024} \right| = 0\\\left| {x + y - 4z} \right| = 0\\{y^2}.\sqrt 5 = 0\end{array}\)
Với \(\left| {x - 2024} \right| = 0\) thì \(x - 2024 = 0\), suy ra \(x = 2024\);
Với \({y^2}.\sqrt 5 = 0\) (do \(\sqrt 5 \ne 0\)) nên \({y^2} = 0\), suy ra \(y = 0\).
Thay \(x = 2024\); \(y = 0\) vào \(\left| {x + y - 4z} \right| = 0\) hay \(x + y - 4z = 0\), ta được
\(2024 + 0 - 4z = 0\) suy ra \(4z = 2024\), do đó \(z = 2024:4 = 506\).
Vậy \(x = 2024;y = 0;z = 506\).
Đề thi giữa kì 1 Toán 7 Kết nối tri thức - Đề số 13 là một bài kiểm tra quan trọng giúp đánh giá mức độ nắm vững kiến thức của học sinh sau một thời gian học tập. Đề thi bao gồm các dạng bài tập khác nhau, từ cơ bản đến nâng cao, đòi hỏi học sinh phải có sự hiểu biết sâu sắc về các khái niệm và kỹ năng toán học đã được học.
Thông thường, đề thi giữa kì 1 Toán 7 Kết nối tri thức - Đề số 13 sẽ bao gồm các phần sau:
Các chủ đề thường xuất hiện trong đề thi bao gồm:
Để đạt kết quả tốt trong kỳ thi giữa kì 1 Toán 7 Kết nối tri thức - Đề số 13, học sinh cần:
Bài 1: Tính giá trị của biểu thức sau: (1/2 + 1/3) * 6
Lời giải:
(1/2 + 1/3) * 6 = (3/6 + 2/6) * 6 = (5/6) * 6 = 5
Việc luyện tập thường xuyên với các đề thi giữa kì 1 Toán 7 Kết nối tri thức - Đề số 13 và các đề thi tương tự là rất quan trọng. Nó giúp học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn trong kỳ thi thực tế.
Giaitoan.edu.vn là một nguồn tài liệu học tập Toán 7 uy tín, cung cấp đầy đủ các đề thi, bài tập, lời giải chi tiết và các tài liệu hỗ trợ học tập khác. Chúng tôi cam kết mang đến cho học sinh những trải nghiệm học tập tốt nhất.
Hãy dành thời gian ôn tập và luyện tập đầy đủ trước kỳ thi giữa kì 1 Toán 7 Kết nối tri thức - Đề số 13. Đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè nếu gặp khó khăn. Chúc các em đạt kết quả tốt nhất!
| Dạng bài tập | Ví dụ |
|---|---|
| Tính toán với số hữu tỉ | Tính: (-2/3) + 1/4 |
| Giải bài toán về tỉ lệ | Một lớp có 30 học sinh, trong đó có 12 học sinh giỏi. Tính tỉ lệ học sinh giỏi của lớp. |
| Biểu diễn số hữu tỉ trên trục số | Biểu diễn số -1/2 trên trục số. |