Chào mừng các em học sinh đến với đề thi giữa kì 2 Toán 7 - Đề số 5 chương trình Kết nối tri thức.
Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong giai đoạn giữa kì 2.
Giaitoan.edu.vn cung cấp đề thi kèm đáp án chi tiết, giúp các em tự học và nâng cao khả năng giải toán.
I. TRẮC NGHIỆM ( 2 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
I. TRẮC NGHIỆM ( 2 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1. Tam giác ABC có \(BC = 1cm,{\mkern 1mu} AC = 8cm.\) Tìm độ dài cạnh AB, biết độ dài này là một số nguyên \(\left( {cm} \right)\).
A. 6cm
B. 7cm
C. 8cm
D. 9cm
Câu 2. Biểu thức đại số biểu thị tổng bình phương của hai số \(a\) và \(b\) là:
A. \({a^2} - {b^2}\)
B. \({a^2} + {b^2}\)
C. \({\left( {a - b} \right)^2}\)
D. \({\left( {a + b} \right)^2}\)
Câu 3. Cho \(\Delta ABC\) có \(AB = 6cm,{\mkern 1mu} BC = 8cm,{\mkern 1mu} AC = 10cm.\) Số đo góc \(\angle A;{\mkern 1mu} \angle B;{\mkern 1mu} \angle C\) theo thứ tự là:
A. \(\angle B < \angle C < \angle A\)
B. \(\angle C < \angle A < \angle B\)
C. \(\angle A > \angle B > \angle C\)
D. \(\angle C < \angle B < \angle A\)
Câu 4. Khẳng định nào sau đây là đúng?
A. Số \(0\) không phải là một đa thức.
B. Nếu \(\Delta ABC\) cân thì trọng tâm, trực tâm, điểm cách đều ba đỉnh, điểm (nằm trong tam giác) cách đều ba cạnh cùng nằm trên một đường thẳng.
C. Nếu \(\Delta ABC\) cân thì trọng tâm, trực tâm, điểm cách đều ba đỉnh, điểm (nằm trong tam giác) cách đều ba cạnh cùng nằm trên một đường tròn.
D. Số \(0\) được gọi là một đa thức không và có bậc bằng \(0\)
Câu 5. Nghiệm của đa thức: \(P\left( x \right) = 15x - 3\) là:
A. \(\dfrac{{ - 1}}{5}\)
B. \(\dfrac{1}{5}\)
C. \(5\)
D. \( - 5\)
Câu 6. Có bao nhiêu đơn thức trong các biểu thức \(2x\,;\,3y\,;\,x - 5y\,;\, - 2x - y; - 1?\)
A. \(2\)
B. \(3\)
C. \(4\)
D. \(5\)
Câu 7. Bậc của đa thức \(10{x^7} + {x^8} - 2x\) là:
A. \(7\)
B. \(8\)
C. \(15\)
D. \(10\)
Câu 8. Nếu đại lượng \(y\) tỉ lệ thuận với đại lượng \(x\) theo hệ số tỉ lệ là 2025 thì đại lượng \(x\) tỉ lệ thuận với đại lượng \(y\) theo hệ số tỉ lệ là:
A. \( - \dfrac{1}{{2025}}\)
B. \(2025\)
C. \(\dfrac{1}{{2025}}\)
D. \( - 2025\)
II. PHẦN TỰ LUẬN (8,0 điểm)
Bài 1. (1,5 điểm) Hai ô tô khởi hành cùng một lúc \(A\) đến \(B\). Xe thứ nhất đi từ \(A\) đến \(B\) hết \(6\) giờ, xe thứ hai đi từ \(B\) đến \(A\) hết \(3\)giờ. Đến chỗ gặp nhau, xe thứ hai đã đi được một quãng đường dài hơn xe thứ nhất đã đi là \(54\) km. Tính quãng đường \(AB\).
Bài 2. (3 điểm) Cho các đa thức sau:
\(P\left( x \right) = - 2x + \dfrac{1}{2}{x^2} + 3{x^4} - 3{x^2} - 3\)
\(Q\left( x \right) = 3{x^4} + {x^3} - 4{x^2} + 1,5{x^3} - 3{x^4} + 2x + 1\)
a) Thu gọn và sắp xếp các đa thức trên theo thứ tự số mũ của biến giảm dần. Xác định bậc, hệ số cao nhất và hệ số tự do của các đa thức đã cho.
b) Xác định \(P\left( x \right) + Q\left( x \right)\),\(P\left( x \right) - Q\left( x \right)\).
c) Xác định đa thức \(R\left( x \right)\)thỏa mãn \(R\left( x \right) + P\left( x \right) - Q\left( x \right) + {x^2} = 2{x^3} - \dfrac{3}{2}x + 1\).
Bài 3. (3 điểm) Cho tam giác ABC cân tại A.Trên cạnh AB lấy điểm M, trên tia đối của tia CA lấy điểm N sao cho AM + AN = 2AB.
a) Chứng minh rằng: BM = CN
b) Chứng minh rằng: BC đi qua trung điểm của đoạn thẳng MN.
c) Đường trung trực của MN và tia phân giác của \(\widehat {BAC}\) cắt nhau tại K. Chứng minh rằng \(\Delta BKM = \Delta CKN\) từ đó suy ra KC vuông góc với AN.
Bài 4. (0,5 điểm) Cho \(a,\,b,\,c \ne 0\) và thỏa mãn \(\dfrac{{a + b - c}}{c} = \dfrac{{c + a - b}}{b} = \dfrac{{b + c - a}}{a}.\) Tính giá trị của biểu thức \(S = \dfrac{{\left( {a + b} \right)\left( {b + c} \right)\left( {c + a} \right)}}{{abc}}.\)
I. Trắc nghiệm
1. C | 2. B | 3. B | 4. B |
5. B | 6. B | 7. B | 8. C |
Câu 1.
Phương pháp:
Áp dụng bất đẳng thức tam giác để tìm cạnh còn lại. Cách giải:
Áp dụng bất đẳng thức cho tam giác ABC ta có:
\(\begin{array}{*{20}{l}}{AC - BC < AB < AC + BC}\\{ \Rightarrow 8 - 1 < AB < 8 + 1}\\{ \Rightarrow 7 < AB < 9}\\{ \Rightarrow AB = 8\left( {cm} \right)}\end{array}\)
ChọnC.
Câu 2.
Phương pháp:
Dùng các chữ, các số và các phép toán để diễn đạt các mệnh đề phát biểu bằng lời.
Cách giải:
Tổng bình phương của hai số \(a\) và \(b\) là: \({a^2} + {b^2}\)
Chọn B.
Câu 3.
Phương pháp:
So sánh độ dài các cạnh rồi dựa vào mối quan hệ giữa cạnh và góc trong một tam giác để so sánh các góc với nhau. Trong một tam giác, góc đối diện với cạnh lớn hơn thì góc lớn hơn. Cách giải:
\(\Delta ABC\) có \(AB = 6cm,{\mkern 1mu} BC = 8cm,{\mkern 1mu} AC = 10cm.\)
Ta có: \(AB < BC < AC\) \( \Rightarrow \angle C < \angle A < \angle B\)
ChọnB.
Câu 4.
Phương pháp:
Áp dụng định nghĩa về đa thức và tính chất tam giác cân. Cách giải:
Xét từng đáp án:
A. Số \(0\) không phải là một đa thức. Sai Vì số 0 là đa thức 0
B. Nếu \(\Delta ABC\) cân thì trọng tâm, trực tâm, điểm cách đều ba đỉnh, điểm (nằm trong tam giác) cách đều ba cạnh cùng nằm trên một đường thẳng. Đúng: (vẽ một tam giác cân và xác định trọng tâm, trực tâm, điểm cách đều 3 đỉnh, điểm nằm trong tam giác và cách đều 3 cạnh ta thấy chúng cùng nằm trên một đường thẳng)
C. Nếu \(\Delta ABC\) cân thì trọng tâm, trực tâm, điểm cách đều ba đỉnh, điểm (nằm trong tam giác) cách đều ba cạnh cùng nằm trên một đường tròn. Sai Vì chúng nằm trên cùng 1 đường thẳng.
D. Số \(0\) được gọi là một đa thức không và có bậc bằng 0. Sai Vì số 0 được gọi là đa thức không và nó là đa thức không có bậc.
Chọn B
Câu 5.
Phương pháp:
Tìm nghiệm của đa thức \(P\left( x \right)\), ta giải phương trình \(P\left( x \right) = 0\)
Cách giải:
Ta có: \(P\left( x \right) = 0\)
\(\begin{array}{l}15x - 3 = 0\\15x = 3\\\,\,\,\,\,x = \dfrac{1}{5}\end{array}\)
Vậy \(x = \dfrac{1}{5}\) là nghiệm của đa thức \(P\left( x \right) = 15x - 3\)
Chọn B.
Câu 6.
Phương pháp:
Đơn thức là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và các biến.
Cách giải:
Biểu thức \(2x\,;\,3y; - 1\) là các đơn thức.
Vậy có \(3\) đơn thức.
Chọn B.
Câu 7.
Phương pháp:
Phương pháp:
Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức đó
Cách giải:
Ta có: hạng tử \({x^8}\) là có bậc cao nhất
\( \Rightarrow \) Bậc của đa thức \(10{x^7} + {x^8} - 2x\) là: \(8\)
Câu 8.
Phương pháp:
Nếu đại lượng \(y\) tỉ lệ thuận với đại lượng \(x\) theo hệ số tỉ lệ \(k\) thì ta có công thức: \(y = kx\)
Cách giải:
Vì đại lượng \(y\) tỉ lệ thuận với đại lượng \(x\) theo hệ số tỉ lệ là 2025 nên ta có công thức: \(y = 2025x\)
Từ đó suy ra \(x = \dfrac{1}{{2025}}y\)
Do đó, đại lượng \(x\) tỉ lệ thuận với đại lượng \(y\) theo hệ số tỉ lệ \(\dfrac{1}{{2025}}\).
Chọn C.
Chú ý: Nếu đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ k thì đại lượng x tỉ lệ thuận với đại lượng y theo hệ số tỉ lệ \(\dfrac{1}{k}\).
II. PHẦN TỰ LUẬN (8,0 điểm)
Bài 1.
Phương pháp:
Tính chất dãy tỉ số bằng nhau: \(\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{{c - a}}{{d - b}}\)
Cách giải:
Gọi quãng đường của xe thứ nhất đi được từ \(A\) đến chỗ gặp là \(x\) (km) \(\left( {x > 0} \right)\)
Gọi quãng đường của xe thứ hai đi được từ \(B\) đến chỗ gặp là \(y\) (km) \(\left( {y > 0} \right)\)
Ta có: \(\dfrac{x}{3} = \dfrac{y}{6}\)
Quãng đường đi được của xe thứ hai dài hơn xe thứ nhất \(54\) km nên \(y - x = 54\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có: \(\dfrac{x}{3} = \dfrac{y}{6} = \dfrac{{y - x}}{{6 - 3}} = \dfrac{{54}}{3} = 18\)
Do đó \(\dfrac{x}{3} = 18 \Rightarrow x = 54\) (thỏa mãn)
\(\dfrac{y}{6} = 18 \Rightarrow y = 108\) (thỏa mãn)
Quãng đường \(AB\) dài là \(54 + 108 = 162\) (km)
Vậy quãng đường \(AB\) dài là \(162\) (km).
Bài 2.
Phương pháp:
+ Để thu gọn đa thức ta thực hiện phép cộng các đơn thức đồng dạng.
+ Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức đó.
+ Ta có thể mở rộng cộng (trừ) các đa thức dựa trên quy tắc “dấu ngoặc” và tính chất của các phép toán trên số.
+ Đối với đa thức một biến đã sắp xếp còn có thể cộng (trừ) bằng cách đặt tính theo cột dọc tương tự cộng (trừ) các số.
Cách giải:
a)
\(\begin{array}{l}P\left( x \right) = - 2x + \dfrac{1}{2}{x^2} + 3{x^4} - 3{x^2} - 3\\\,\,\,\,\,\,\,\,\,\,\,\, = 3{x^4} + \dfrac{1}{2}{x^2} - 3{x^2} - 2x - 3\\\,\,\,\,\,\,\,\,\,\,\,\, = 3{x^4} - \dfrac{5}{2}{x^2} - 2x - 3\end{array}\)
Vậy: \(P\) có bậc là \(4\); Hệ số cao nhất là \(3\); Hệ số tự do là \( - 3\)
\(\begin{array}{l}Q\left( x \right) = 3{x^4} + {x^3} - 4{x^2} + 1,5{x^3} - 3{x^4} + 2x + 1\\\,\,\,\,\,\,\,\,\,\,\,\, = 3{x^4} - 3{x^4} + {x^3} + 1,5{x^3} - 4{x^2} + 2x + 1\\\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{5}{2}{x^3} - 4{x^2} + 2x + 1\end{array}\)
Vậy: \(Q\) có bậc là \(3\); Hệ số cao nhất là \(\dfrac{5}{2}\); Hệ số tự do là \(1\)
b)
\(\begin{array}{l}P\left( x \right) + Q\left( x \right) = \left( {3{x^4} - \dfrac{5}{2}{x^2} - 2x - 3} \right) + \left( {\dfrac{5}{2}{x^3} - 4{x^2} + 2x + 1} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 3{x^4} + \dfrac{5}{2}{x^3} - \dfrac{5}{2}{x^2} - 4{x^2} - 2x + 2x - 3 + 1\end{array}\)
\( = 3{x^4} + \dfrac{5}{2}{x^3} - \dfrac{{13}}{2}{x^2} - 2\)
\(\begin{array}{l}P\left( x \right) - Q\left( x \right) = \left( {3{x^4} - \dfrac{5}{2}{x^2} - 2x - 3} \right) - \left( {\dfrac{5}{2}{x^3} - 4{x^2} + 2x + 1} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 3{x^4} - \dfrac{5}{2}{x^2} - 2x - 3 - \dfrac{5}{2}{x^3} + 4{x^2} - 2x - 1\end{array}\)
\(\begin{array}{l} = 3{x^4} - \dfrac{5}{2}{x^3} - \dfrac{5}{2}{x^2} + 4{x^2} - 2x - 2x - 3 - 1\\ = 3{x^4} - \dfrac{5}{2}{x^3} + \dfrac{3}{2}{x^2} - 4x - 4\end{array}\)
c) \(R\left( x \right) + P\left( x \right) - Q\left( x \right) + {x^2} = 2{x^3} - \dfrac{3}{2}x + 1\)
\( \Leftrightarrow R\left( x \right) + \left( {3{x^4} + \dfrac{5}{2}{x^3} - \dfrac{{13}}{2}{x^2} - 2} \right) - \left( {3{x^4} - \dfrac{5}{2}{x^3} + \dfrac{3}{2}{x^2} - 4x - 4} \right) + {x^2} = 2{x^3} - \dfrac{3}{2}x + 1\)
\( \Leftrightarrow R\left( x \right) + 3{x^4} - 3{x^4} + \dfrac{5}{2}{x^3} + \dfrac{5}{2}{x^3} - \dfrac{{13}}{2}{x^2} - \dfrac{3}{2}{x^2} + {x^2} + 4x - 2 + 4 = 2{x^3} - \dfrac{3}{2}x + 1\)
\( \Leftrightarrow R\left( x \right) + 5{x^3} - 7{x^2} + 4x + 2 = 2{x^3} - \dfrac{3}{2}x + 1\)
\(\begin{array}{l} \Leftrightarrow R\left( x \right) = 2{x^3} - \dfrac{3}{2}x + 1 - \left( {5{x^3} - 7{x^2} + 4x + 2} \right)\\ \Leftrightarrow R\left( x \right) = 2{x^3} - \dfrac{3}{2}x + 1 - 5{x^3} + 7{x^2} - 4x - 2\end{array}\)
\(\begin{array}{l} \Leftrightarrow R\left( x \right) = 2{x^3} - 5{x^3} + 7{x^2} - \dfrac{3}{2}x - 4x - 2 + 1\\ \Leftrightarrow R\left( x \right) = - 3{x^3} + 7{x^2} - \dfrac{{11}}{2}x - 1\end{array}\)
Bài 3.
Phương pháp:
a) Sử dụng tính chất tam giác cân, sau đó dùng giả thiết đã cho lập luận để suy ra điều phải chứng minh.
b) Sử dụng các trường hợp bằng nhau của tam giác để suy ra các cặp tam giác bằng nhau, từ đó suy ra điều phải chứng minh.
c) Sử dụng các trường hợp bằng nhau của tam giác để chứng minh hai góc bằng nhau, sử dụng thêm tính chất hai góc kề bù để suy ra điều phải chứng minh. Cách giải:
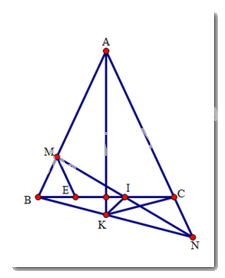
a) Do tam giác ABC cân tại A, suy ra AB = AC.
Ta có: AM + AN = AB – BM + AC + CN = 2AB – BM + CN.
Ta lại có AM + AN = 2AB(gt), nên suy ra \(2AB - BM + CN = 2AB\).
\( \Leftrightarrow - BM + CN = 0 \Leftrightarrow BM = CN\)
b) Gọi I là giao điểm của MN và BC. Vậy BM = CN (đpcm)
Qua M kẻ đường thẳng song song với AC cắt BC tại E.
Do ME // NC nên ta có:
\(\widehat {IME} = \widehat {CNI}\)(hai góc so le trong)
\(\widehat {MEI} = \widehat {NCI}\)(hai góc so le trong)
\(\widehat {MEB} = \widehat {ACB}\) (hai góc đồng vị) nên \(\widehat {MEB} = \widehat {ABC} \Rightarrow \Delta MBE\)cân tại M nên MB = ME. Do đó, ME = CN.
Ta chứng minh được \(\Delta MEI = \Delta NCI{\mkern 1mu} {\mkern 1mu} (g.c.g)\)
Suy ra MI = NI (hai cạnh tương ứng), từ đó suy ra I là trung điểm của MN.
c) Xét hai tam giác MIK và NIK có:
MI = IN (cmt), \(\widehat {MIK} = \widehat {NIK} = {90^0}\)
IK là cạnh chung. Do đó \(\Delta MIK = \Delta NIK(c.g.c)\).
Suy ra KM = KN (hai cạnh tương ứng).
Xét hai tam giác ABK và ACK có:
AB = AC(gt),
\(\widehat {BAK} = \widehat {CAK}\) (do BK là tia phân giác của góc BAC),
AK là cạnh chung,
Do đó \(\Delta ABK = \Delta ACK(c.g.c)\).
Suy ra KB = KC (hai cạnh tương ứng).
Xét hai tam giác BKM và CKN có:
MB = CN, BK = KN, MK = KC,
Do đó \(\Delta BKM = \Delta CKN(c.c.c)\),
Suy ra \(\widehat {MBK} = \widehat {KCN}\).
Mà \(\widehat {MBK} = \widehat {ACK} \Rightarrow \widehat {ACK} = \widehat {KCN} = {180^0}:2 = {90^0} \Rightarrow KC \bot AN.\)(đpcm)
Bài 4.
Áp dụng tính chất của dãy tỉ số bằng nhau.
Cách giải:
- Trường hợp \(1:\,a,\,b,\,c \ne 0\) và \(a + b + c = 0 \Rightarrow a + b = - c;\,\,a + c = - b;\,\,b + c = - a\) thay vảo biểu thức \(S\) ta được:
\(S = \dfrac{{ - c.\left( { - a} \right).\left( { - b} \right)}}{{abc}} = - 1.\)
- Trường hợp 2: \(a,\,b,\,c \ne 0\) và \(a + b + c \ne 0.\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta được:
\(\dfrac{{a + b - c}}{c} = \dfrac{{c + a - b}}{b} = \dfrac{{b + c - a}}{a} = \dfrac{{a + b - c + c + a - b + b + c - a}}{{c + b + a}} = 1\)
Suy ra \(\left\{ \begin{array}{l}a + b = 2c\\c + a = 2b\\b + c = 2a\end{array} \right.\) thay vào biểu thức \(S\) ta được:
\(S = \dfrac{{2c.2a.2b}}{{abc}} = 8\)
Vậy: \(S = - 1\) khi \(\dfrac{{a + b - c}}{c} = \dfrac{{c + a - b}}{b} = \dfrac{{b + c - a}}{a}\) và \(a,\,b,\,c \ne 0;\) \(a + b + c = 0\)
\(S = 8\) khi \(\dfrac{{a + b - c}}{c} = \dfrac{{c + a - b}}{b} = \dfrac{{b + c - a}}{a}\) và \(a,\,b,\,c \ne 0;\) \(a + b + c \ne 0\).
I. TRẮC NGHIỆM ( 2 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1. Tam giác ABC có \(BC = 1cm,{\mkern 1mu} AC = 8cm.\) Tìm độ dài cạnh AB, biết độ dài này là một số nguyên \(\left( {cm} \right)\).
A. 6cm
B. 7cm
C. 8cm
D. 9cm
Câu 2. Biểu thức đại số biểu thị tổng bình phương của hai số \(a\) và \(b\) là:
A. \({a^2} - {b^2}\)
B. \({a^2} + {b^2}\)
C. \({\left( {a - b} \right)^2}\)
D. \({\left( {a + b} \right)^2}\)
Câu 3. Cho \(\Delta ABC\) có \(AB = 6cm,{\mkern 1mu} BC = 8cm,{\mkern 1mu} AC = 10cm.\) Số đo góc \(\angle A;{\mkern 1mu} \angle B;{\mkern 1mu} \angle C\) theo thứ tự là:
A. \(\angle B < \angle C < \angle A\)
B. \(\angle C < \angle A < \angle B\)
C. \(\angle A > \angle B > \angle C\)
D. \(\angle C < \angle B < \angle A\)
Câu 4. Khẳng định nào sau đây là đúng?
A. Số \(0\) không phải là một đa thức.
B. Nếu \(\Delta ABC\) cân thì trọng tâm, trực tâm, điểm cách đều ba đỉnh, điểm (nằm trong tam giác) cách đều ba cạnh cùng nằm trên một đường thẳng.
C. Nếu \(\Delta ABC\) cân thì trọng tâm, trực tâm, điểm cách đều ba đỉnh, điểm (nằm trong tam giác) cách đều ba cạnh cùng nằm trên một đường tròn.
D. Số \(0\) được gọi là một đa thức không và có bậc bằng \(0\)
Câu 5. Nghiệm của đa thức: \(P\left( x \right) = 15x - 3\) là:
A. \(\dfrac{{ - 1}}{5}\)
B. \(\dfrac{1}{5}\)
C. \(5\)
D. \( - 5\)
Câu 6. Có bao nhiêu đơn thức trong các biểu thức \(2x\,;\,3y\,;\,x - 5y\,;\, - 2x - y; - 1?\)
A. \(2\)
B. \(3\)
C. \(4\)
D. \(5\)
Câu 7. Bậc của đa thức \(10{x^7} + {x^8} - 2x\) là:
A. \(7\)
B. \(8\)
C. \(15\)
D. \(10\)
Câu 8. Nếu đại lượng \(y\) tỉ lệ thuận với đại lượng \(x\) theo hệ số tỉ lệ là 2025 thì đại lượng \(x\) tỉ lệ thuận với đại lượng \(y\) theo hệ số tỉ lệ là:
A. \( - \dfrac{1}{{2025}}\)
B. \(2025\)
C. \(\dfrac{1}{{2025}}\)
D. \( - 2025\)
II. PHẦN TỰ LUẬN (8,0 điểm)
Bài 1. (1,5 điểm) Hai ô tô khởi hành cùng một lúc \(A\) đến \(B\). Xe thứ nhất đi từ \(A\) đến \(B\) hết \(6\) giờ, xe thứ hai đi từ \(B\) đến \(A\) hết \(3\)giờ. Đến chỗ gặp nhau, xe thứ hai đã đi được một quãng đường dài hơn xe thứ nhất đã đi là \(54\) km. Tính quãng đường \(AB\).
Bài 2. (3 điểm) Cho các đa thức sau:
\(P\left( x \right) = - 2x + \dfrac{1}{2}{x^2} + 3{x^4} - 3{x^2} - 3\)
\(Q\left( x \right) = 3{x^4} + {x^3} - 4{x^2} + 1,5{x^3} - 3{x^4} + 2x + 1\)
a) Thu gọn và sắp xếp các đa thức trên theo thứ tự số mũ của biến giảm dần. Xác định bậc, hệ số cao nhất và hệ số tự do của các đa thức đã cho.
b) Xác định \(P\left( x \right) + Q\left( x \right)\),\(P\left( x \right) - Q\left( x \right)\).
c) Xác định đa thức \(R\left( x \right)\)thỏa mãn \(R\left( x \right) + P\left( x \right) - Q\left( x \right) + {x^2} = 2{x^3} - \dfrac{3}{2}x + 1\).
Bài 3. (3 điểm) Cho tam giác ABC cân tại A.Trên cạnh AB lấy điểm M, trên tia đối của tia CA lấy điểm N sao cho AM + AN = 2AB.
a) Chứng minh rằng: BM = CN
b) Chứng minh rằng: BC đi qua trung điểm của đoạn thẳng MN.
c) Đường trung trực của MN và tia phân giác của \(\widehat {BAC}\) cắt nhau tại K. Chứng minh rằng \(\Delta BKM = \Delta CKN\) từ đó suy ra KC vuông góc với AN.
Bài 4. (0,5 điểm) Cho \(a,\,b,\,c \ne 0\) và thỏa mãn \(\dfrac{{a + b - c}}{c} = \dfrac{{c + a - b}}{b} = \dfrac{{b + c - a}}{a}.\) Tính giá trị của biểu thức \(S = \dfrac{{\left( {a + b} \right)\left( {b + c} \right)\left( {c + a} \right)}}{{abc}}.\)
I. Trắc nghiệm
1. C | 2. B | 3. B | 4. B |
5. B | 6. B | 7. B | 8. C |
Câu 1.
Phương pháp:
Áp dụng bất đẳng thức tam giác để tìm cạnh còn lại. Cách giải:
Áp dụng bất đẳng thức cho tam giác ABC ta có:
\(\begin{array}{*{20}{l}}{AC - BC < AB < AC + BC}\\{ \Rightarrow 8 - 1 < AB < 8 + 1}\\{ \Rightarrow 7 < AB < 9}\\{ \Rightarrow AB = 8\left( {cm} \right)}\end{array}\)
ChọnC.
Câu 2.
Phương pháp:
Dùng các chữ, các số và các phép toán để diễn đạt các mệnh đề phát biểu bằng lời.
Cách giải:
Tổng bình phương của hai số \(a\) và \(b\) là: \({a^2} + {b^2}\)
Chọn B.
Câu 3.
Phương pháp:
So sánh độ dài các cạnh rồi dựa vào mối quan hệ giữa cạnh và góc trong một tam giác để so sánh các góc với nhau. Trong một tam giác, góc đối diện với cạnh lớn hơn thì góc lớn hơn. Cách giải:
\(\Delta ABC\) có \(AB = 6cm,{\mkern 1mu} BC = 8cm,{\mkern 1mu} AC = 10cm.\)
Ta có: \(AB < BC < AC\) \( \Rightarrow \angle C < \angle A < \angle B\)
ChọnB.
Câu 4.
Phương pháp:
Áp dụng định nghĩa về đa thức và tính chất tam giác cân. Cách giải:
Xét từng đáp án:
A. Số \(0\) không phải là một đa thức. Sai Vì số 0 là đa thức 0
B. Nếu \(\Delta ABC\) cân thì trọng tâm, trực tâm, điểm cách đều ba đỉnh, điểm (nằm trong tam giác) cách đều ba cạnh cùng nằm trên một đường thẳng. Đúng: (vẽ một tam giác cân và xác định trọng tâm, trực tâm, điểm cách đều 3 đỉnh, điểm nằm trong tam giác và cách đều 3 cạnh ta thấy chúng cùng nằm trên một đường thẳng)
C. Nếu \(\Delta ABC\) cân thì trọng tâm, trực tâm, điểm cách đều ba đỉnh, điểm (nằm trong tam giác) cách đều ba cạnh cùng nằm trên một đường tròn. Sai Vì chúng nằm trên cùng 1 đường thẳng.
D. Số \(0\) được gọi là một đa thức không và có bậc bằng 0. Sai Vì số 0 được gọi là đa thức không và nó là đa thức không có bậc.
Chọn B
Câu 5.
Phương pháp:
Tìm nghiệm của đa thức \(P\left( x \right)\), ta giải phương trình \(P\left( x \right) = 0\)
Cách giải:
Ta có: \(P\left( x \right) = 0\)
\(\begin{array}{l}15x - 3 = 0\\15x = 3\\\,\,\,\,\,x = \dfrac{1}{5}\end{array}\)
Vậy \(x = \dfrac{1}{5}\) là nghiệm của đa thức \(P\left( x \right) = 15x - 3\)
Chọn B.
Câu 6.
Phương pháp:
Đơn thức là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và các biến.
Cách giải:
Biểu thức \(2x\,;\,3y; - 1\) là các đơn thức.
Vậy có \(3\) đơn thức.
Chọn B.
Câu 7.
Phương pháp:
Phương pháp:
Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức đó
Cách giải:
Ta có: hạng tử \({x^8}\) là có bậc cao nhất
\( \Rightarrow \) Bậc của đa thức \(10{x^7} + {x^8} - 2x\) là: \(8\)
Câu 8.
Phương pháp:
Nếu đại lượng \(y\) tỉ lệ thuận với đại lượng \(x\) theo hệ số tỉ lệ \(k\) thì ta có công thức: \(y = kx\)
Cách giải:
Vì đại lượng \(y\) tỉ lệ thuận với đại lượng \(x\) theo hệ số tỉ lệ là 2025 nên ta có công thức: \(y = 2025x\)
Từ đó suy ra \(x = \dfrac{1}{{2025}}y\)
Do đó, đại lượng \(x\) tỉ lệ thuận với đại lượng \(y\) theo hệ số tỉ lệ \(\dfrac{1}{{2025}}\).
Chọn C.
Chú ý: Nếu đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ k thì đại lượng x tỉ lệ thuận với đại lượng y theo hệ số tỉ lệ \(\dfrac{1}{k}\).
II. PHẦN TỰ LUẬN (8,0 điểm)
Bài 1.
Phương pháp:
Tính chất dãy tỉ số bằng nhau: \(\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{{c - a}}{{d - b}}\)
Cách giải:
Gọi quãng đường của xe thứ nhất đi được từ \(A\) đến chỗ gặp là \(x\) (km) \(\left( {x > 0} \right)\)
Gọi quãng đường của xe thứ hai đi được từ \(B\) đến chỗ gặp là \(y\) (km) \(\left( {y > 0} \right)\)
Ta có: \(\dfrac{x}{3} = \dfrac{y}{6}\)
Quãng đường đi được của xe thứ hai dài hơn xe thứ nhất \(54\) km nên \(y - x = 54\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có: \(\dfrac{x}{3} = \dfrac{y}{6} = \dfrac{{y - x}}{{6 - 3}} = \dfrac{{54}}{3} = 18\)
Do đó \(\dfrac{x}{3} = 18 \Rightarrow x = 54\) (thỏa mãn)
\(\dfrac{y}{6} = 18 \Rightarrow y = 108\) (thỏa mãn)
Quãng đường \(AB\) dài là \(54 + 108 = 162\) (km)
Vậy quãng đường \(AB\) dài là \(162\) (km).
Bài 2.
Phương pháp:
+ Để thu gọn đa thức ta thực hiện phép cộng các đơn thức đồng dạng.
+ Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức đó.
+ Ta có thể mở rộng cộng (trừ) các đa thức dựa trên quy tắc “dấu ngoặc” và tính chất của các phép toán trên số.
+ Đối với đa thức một biến đã sắp xếp còn có thể cộng (trừ) bằng cách đặt tính theo cột dọc tương tự cộng (trừ) các số.
Cách giải:
a)
\(\begin{array}{l}P\left( x \right) = - 2x + \dfrac{1}{2}{x^2} + 3{x^4} - 3{x^2} - 3\\\,\,\,\,\,\,\,\,\,\,\,\, = 3{x^4} + \dfrac{1}{2}{x^2} - 3{x^2} - 2x - 3\\\,\,\,\,\,\,\,\,\,\,\,\, = 3{x^4} - \dfrac{5}{2}{x^2} - 2x - 3\end{array}\)
Vậy: \(P\) có bậc là \(4\); Hệ số cao nhất là \(3\); Hệ số tự do là \( - 3\)
\(\begin{array}{l}Q\left( x \right) = 3{x^4} + {x^3} - 4{x^2} + 1,5{x^3} - 3{x^4} + 2x + 1\\\,\,\,\,\,\,\,\,\,\,\,\, = 3{x^4} - 3{x^4} + {x^3} + 1,5{x^3} - 4{x^2} + 2x + 1\\\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{5}{2}{x^3} - 4{x^2} + 2x + 1\end{array}\)
Vậy: \(Q\) có bậc là \(3\); Hệ số cao nhất là \(\dfrac{5}{2}\); Hệ số tự do là \(1\)
b)
\(\begin{array}{l}P\left( x \right) + Q\left( x \right) = \left( {3{x^4} - \dfrac{5}{2}{x^2} - 2x - 3} \right) + \left( {\dfrac{5}{2}{x^3} - 4{x^2} + 2x + 1} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 3{x^4} + \dfrac{5}{2}{x^3} - \dfrac{5}{2}{x^2} - 4{x^2} - 2x + 2x - 3 + 1\end{array}\)
\( = 3{x^4} + \dfrac{5}{2}{x^3} - \dfrac{{13}}{2}{x^2} - 2\)
\(\begin{array}{l}P\left( x \right) - Q\left( x \right) = \left( {3{x^4} - \dfrac{5}{2}{x^2} - 2x - 3} \right) - \left( {\dfrac{5}{2}{x^3} - 4{x^2} + 2x + 1} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 3{x^4} - \dfrac{5}{2}{x^2} - 2x - 3 - \dfrac{5}{2}{x^3} + 4{x^2} - 2x - 1\end{array}\)
\(\begin{array}{l} = 3{x^4} - \dfrac{5}{2}{x^3} - \dfrac{5}{2}{x^2} + 4{x^2} - 2x - 2x - 3 - 1\\ = 3{x^4} - \dfrac{5}{2}{x^3} + \dfrac{3}{2}{x^2} - 4x - 4\end{array}\)
c) \(R\left( x \right) + P\left( x \right) - Q\left( x \right) + {x^2} = 2{x^3} - \dfrac{3}{2}x + 1\)
\( \Leftrightarrow R\left( x \right) + \left( {3{x^4} + \dfrac{5}{2}{x^3} - \dfrac{{13}}{2}{x^2} - 2} \right) - \left( {3{x^4} - \dfrac{5}{2}{x^3} + \dfrac{3}{2}{x^2} - 4x - 4} \right) + {x^2} = 2{x^3} - \dfrac{3}{2}x + 1\)
\( \Leftrightarrow R\left( x \right) + 3{x^4} - 3{x^4} + \dfrac{5}{2}{x^3} + \dfrac{5}{2}{x^3} - \dfrac{{13}}{2}{x^2} - \dfrac{3}{2}{x^2} + {x^2} + 4x - 2 + 4 = 2{x^3} - \dfrac{3}{2}x + 1\)
\( \Leftrightarrow R\left( x \right) + 5{x^3} - 7{x^2} + 4x + 2 = 2{x^3} - \dfrac{3}{2}x + 1\)
\(\begin{array}{l} \Leftrightarrow R\left( x \right) = 2{x^3} - \dfrac{3}{2}x + 1 - \left( {5{x^3} - 7{x^2} + 4x + 2} \right)\\ \Leftrightarrow R\left( x \right) = 2{x^3} - \dfrac{3}{2}x + 1 - 5{x^3} + 7{x^2} - 4x - 2\end{array}\)
\(\begin{array}{l} \Leftrightarrow R\left( x \right) = 2{x^3} - 5{x^3} + 7{x^2} - \dfrac{3}{2}x - 4x - 2 + 1\\ \Leftrightarrow R\left( x \right) = - 3{x^3} + 7{x^2} - \dfrac{{11}}{2}x - 1\end{array}\)
Bài 3.
Phương pháp:
a) Sử dụng tính chất tam giác cân, sau đó dùng giả thiết đã cho lập luận để suy ra điều phải chứng minh.
b) Sử dụng các trường hợp bằng nhau của tam giác để suy ra các cặp tam giác bằng nhau, từ đó suy ra điều phải chứng minh.
c) Sử dụng các trường hợp bằng nhau của tam giác để chứng minh hai góc bằng nhau, sử dụng thêm tính chất hai góc kề bù để suy ra điều phải chứng minh. Cách giải:
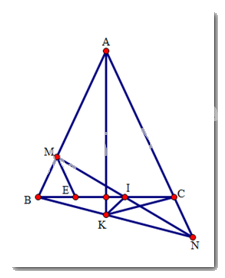
a) Do tam giác ABC cân tại A, suy ra AB = AC.
Ta có: AM + AN = AB – BM + AC + CN = 2AB – BM + CN.
Ta lại có AM + AN = 2AB(gt), nên suy ra \(2AB - BM + CN = 2AB\).
\( \Leftrightarrow - BM + CN = 0 \Leftrightarrow BM = CN\)
b) Gọi I là giao điểm của MN và BC. Vậy BM = CN (đpcm)
Qua M kẻ đường thẳng song song với AC cắt BC tại E.
Do ME // NC nên ta có:
\(\widehat {IME} = \widehat {CNI}\)(hai góc so le trong)
\(\widehat {MEI} = \widehat {NCI}\)(hai góc so le trong)
\(\widehat {MEB} = \widehat {ACB}\) (hai góc đồng vị) nên \(\widehat {MEB} = \widehat {ABC} \Rightarrow \Delta MBE\)cân tại M nên MB = ME. Do đó, ME = CN.
Ta chứng minh được \(\Delta MEI = \Delta NCI{\mkern 1mu} {\mkern 1mu} (g.c.g)\)
Suy ra MI = NI (hai cạnh tương ứng), từ đó suy ra I là trung điểm của MN.
c) Xét hai tam giác MIK và NIK có:
MI = IN (cmt), \(\widehat {MIK} = \widehat {NIK} = {90^0}\)
IK là cạnh chung. Do đó \(\Delta MIK = \Delta NIK(c.g.c)\).
Suy ra KM = KN (hai cạnh tương ứng).
Xét hai tam giác ABK và ACK có:
AB = AC(gt),
\(\widehat {BAK} = \widehat {CAK}\) (do BK là tia phân giác của góc BAC),
AK là cạnh chung,
Do đó \(\Delta ABK = \Delta ACK(c.g.c)\).
Suy ra KB = KC (hai cạnh tương ứng).
Xét hai tam giác BKM và CKN có:
MB = CN, BK = KN, MK = KC,
Do đó \(\Delta BKM = \Delta CKN(c.c.c)\),
Suy ra \(\widehat {MBK} = \widehat {KCN}\).
Mà \(\widehat {MBK} = \widehat {ACK} \Rightarrow \widehat {ACK} = \widehat {KCN} = {180^0}:2 = {90^0} \Rightarrow KC \bot AN.\)(đpcm)
Bài 4.
Áp dụng tính chất của dãy tỉ số bằng nhau.
Cách giải:
- Trường hợp \(1:\,a,\,b,\,c \ne 0\) và \(a + b + c = 0 \Rightarrow a + b = - c;\,\,a + c = - b;\,\,b + c = - a\) thay vảo biểu thức \(S\) ta được:
\(S = \dfrac{{ - c.\left( { - a} \right).\left( { - b} \right)}}{{abc}} = - 1.\)
- Trường hợp 2: \(a,\,b,\,c \ne 0\) và \(a + b + c \ne 0.\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta được:
\(\dfrac{{a + b - c}}{c} = \dfrac{{c + a - b}}{b} = \dfrac{{b + c - a}}{a} = \dfrac{{a + b - c + c + a - b + b + c - a}}{{c + b + a}} = 1\)
Suy ra \(\left\{ \begin{array}{l}a + b = 2c\\c + a = 2b\\b + c = 2a\end{array} \right.\) thay vào biểu thức \(S\) ta được:
\(S = \dfrac{{2c.2a.2b}}{{abc}} = 8\)
Vậy: \(S = - 1\) khi \(\dfrac{{a + b - c}}{c} = \dfrac{{c + a - b}}{b} = \dfrac{{b + c - a}}{a}\) và \(a,\,b,\,c \ne 0;\) \(a + b + c = 0\)
\(S = 8\) khi \(\dfrac{{a + b - c}}{c} = \dfrac{{c + a - b}}{b} = \dfrac{{b + c - a}}{a}\) và \(a,\,b,\,c \ne 0;\) \(a + b + c \ne 0\).
Đề thi giữa kì 2 Toán 7 - Đề số 5 chương trình Kết nối tri thức là một công cụ quan trọng giúp học sinh đánh giá mức độ nắm vững kiến thức đã học trong giai đoạn giữa học kì. Đề thi bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính như biểu thức đại số, phương trình bậc nhất một ẩn, bất đẳng thức, và các ứng dụng thực tế của toán học.
Đề thi thường được chia thành các phần sau:
Phần này tập trung vào việc thu gọn biểu thức, tìm giá trị của biểu thức, và thực hiện các phép toán trên biểu thức đại số. Học sinh cần nắm vững các quy tắc về dấu ngoặc, thứ tự thực hiện các phép toán, và các tính chất của phép cộng, trừ, nhân, chia.
Học sinh cần biết cách giải phương trình bậc nhất một ẩn, kiểm tra nghiệm của phương trình, và ứng dụng phương trình để giải các bài toán thực tế. Các dạng bài tập thường gặp bao gồm giải phương trình, tìm điều kiện xác định của phương trình, và giải bài toán bằng cách lập phương trình.
Phần này tập trung vào việc giải bất đẳng thức, biểu diễn tập nghiệm của bất đẳng thức trên trục số, và ứng dụng bất đẳng thức để giải các bài toán thực tế. Học sinh cần nắm vững các quy tắc về bất đẳng thức, các phép biến đổi bất đẳng thức, và các tính chất của bất đẳng thức.
Phần này yêu cầu học sinh áp dụng kiến thức đã học để giải quyết các bài toán thực tế liên quan đến các lĩnh vực khác nhau như kinh tế, kỹ thuật, và khoa học. Các bài toán ứng dụng thường đòi hỏi học sinh phải phân tích đề bài, xác định các yếu tố liên quan, và xây dựng mô hình toán học để giải quyết vấn đề.
Giaitoan.edu.vn cung cấp đáp án chi tiết và lời giải cho từng bài tập trong đề thi. Các lời giải được trình bày một cách rõ ràng, dễ hiểu, giúp học sinh nắm vững phương pháp giải và tự tin hơn khi làm bài.
Đề thi giữa kì 2 Toán 7 - Đề số 5 - Kết nối tri thức là một tài liệu học tập hữu ích giúp học sinh ôn tập kiến thức, đánh giá năng lực, và chuẩn bị cho kỳ thi. Hãy luyện tập thường xuyên và tham khảo đáp án chi tiết để đạt kết quả tốt nhất!