Chào mừng các em học sinh lớp 7 đến với đề thi học kì 1 môn Toán chương trình Kết nối tri thức - Đề số 16.
Đề thi này được thiết kế bám sát cấu trúc đề thi chính thức, giúp các em làm quen với dạng bài và rèn luyện kỹ năng giải quyết vấn đề.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Trong các số sau, số nào là số vô tỉ?
\(\sqrt 3 \).
\(\frac{{ - 13}}{9}\).
\(0\).
\(2023\).
Giá trị tuyệt đối của \(\frac{{ - 15}}{{19}}\) là:
\(\frac{{ - 15}}{{19}}\).
\(\frac{{19}}{{15}}\).
\(\frac{{15}}{{19}}\).
\(\frac{{19}}{{ - 15}}\).
Kết quả làm tròn số 2,4379 đến chữ số thập phân thứ ba là:
2,4.
2,439.
2,437.
2,438.
Cho biểu đồ sau: Tháng có nhiệt đô cao nhất là?
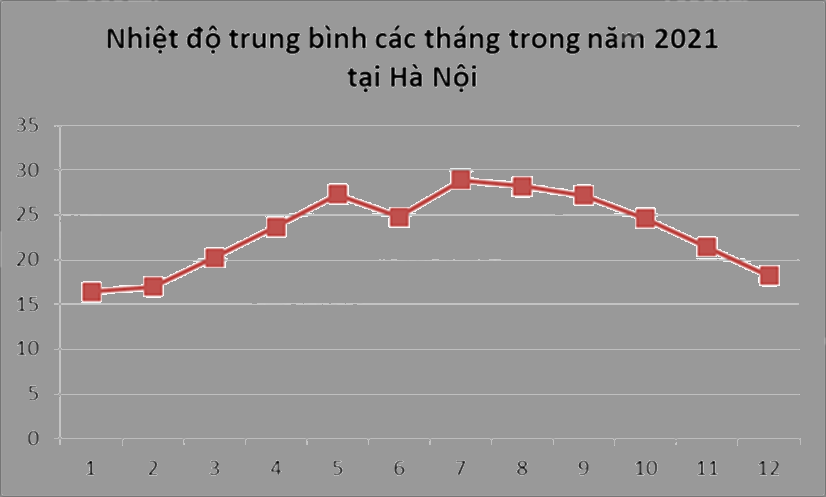
Tháng 1.
Tháng 5.
Tháng 7.
Tháng 8.
Cho \(\Delta MNP = \Delta DHK\). Khẳng định nào sau đây là đúng:
NP = DH.
MN = DK.
\(\widehat {MPN} = \widehat {HDK}\).
\(\widehat {MNP} = \widehat {DHK}\).
Cho tam giác ABC cân tại A, khẳng định nào sau đây SAI?
AB = BC.
AB = AC.
\(\widehat B = \widehat C\).
\(\widehat B = \frac{{180^\circ - \widehat A}}{2}\).
Thực hiện phép tính:
a) \( - 0,5 + \frac{3}{4}\)
b) \({\left( { - \frac{2}{3}} \right)^2}.\frac{9}{{16}} + \sqrt {\frac{4}{{81}}} :\frac{{16}}{9} - \left| { - \frac{9}{{16}}} \right|.\frac{2}{3}\)
Tìm \(x\), biết:
a) \(\frac{4}{3} + x = \frac{{ - 1}}{6}\)
b) \(2\left| {\frac{4}{5} - 2x} \right| + \frac{3}{5} = 3\)
Tỉ lệ phần trăm học sinh của khối 7 thích chơi các môn thể thao được thống kê theo bảng sau:

a) Hãy vẽ biểu đồ hình quạt tròn.
b) Biết số học sinh khối 7 là 320 học sinh. Tính số học sinh thích chơi đá cầu.
Cho tam giác ABC nhọn có AB = AC. Gọi M là trung điểm của đoạn thẳng BC.
a) Chứng minh \(\Delta ABM = \Delta ACM\).
b) Chứng minh \(AM \bot BC\).
c) Trên tia đối của tia MA lấy điểm E sao cho \(MA = ME\). Kẻ \(BH \bot AC\) tại H, \(CK \bot BE\) tại K. Chứng minh \(AC//BE\) và M là trung điểm của đoạn thẳng HK.
Cho \(A = \frac{1}{3} + \frac{1}{{{3^3}}} + \frac{1}{{{3^5}}} + \frac{1}{{{3^7}}} + ... + \frac{1}{{{3^{2023}}}}\). Chứng minh rằng \(A < \frac{3}{8}\).
Trong các số sau, số nào là số vô tỉ?
\(\sqrt 3 \).
\(\frac{{ - 13}}{9}\).
\(0\).
\(2023\).
Đáp án : A
Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn.
Các số \(\frac{{ - 13}}{9}\); 0; 2023 là các số hữu tỉ, không là các số số tỉ.
Chỉ có số \(\sqrt 3 \) là số vô tỉ.
Đáp án A
Giá trị tuyệt đối của \(\frac{{ - 15}}{{19}}\) là:
\(\frac{{ - 15}}{{19}}\).
\(\frac{{19}}{{15}}\).
\(\frac{{15}}{{19}}\).
\(\frac{{19}}{{ - 15}}\).
Đáp án : C
Sử dụng kiến thức giá trị tuyệt đối của một số thực:
|a| = a nếu a \( \ge \) 0.
|a| = -a nếu a < 0.
Giá trị tuyệt đối của \(\frac{{ - 15}}{{19}}\) là: \(\left| {\frac{{ - 15}}{{19}}} \right| = \frac{{15}}{{19}}\).
Đáp án C
Kết quả làm tròn số 2,4379 đến chữ số thập phân thứ ba là:
2,4.
2,439.
2,437.
2,438.
Đáp án : D
Áp dụng quy tắc Làm tròn số thập phân dương:
- Đối với chữ số hàng làm tròn:
+ Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn 5;
+ Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hoặc bằng 5.
- Đối với chữ số sau hàng làm tròn:
+ Bỏ đi nếu ở phần thập phân;
+ Thay bằng các chữ số 0 nếu ở phần số nguyên.
Số 2,4379 làm tròn đến chữ số thập phân thứ ba là 2,438 (vì 9 > 5).
Đáp án D
Cho biểu đồ sau: Tháng có nhiệt đô cao nhất là?
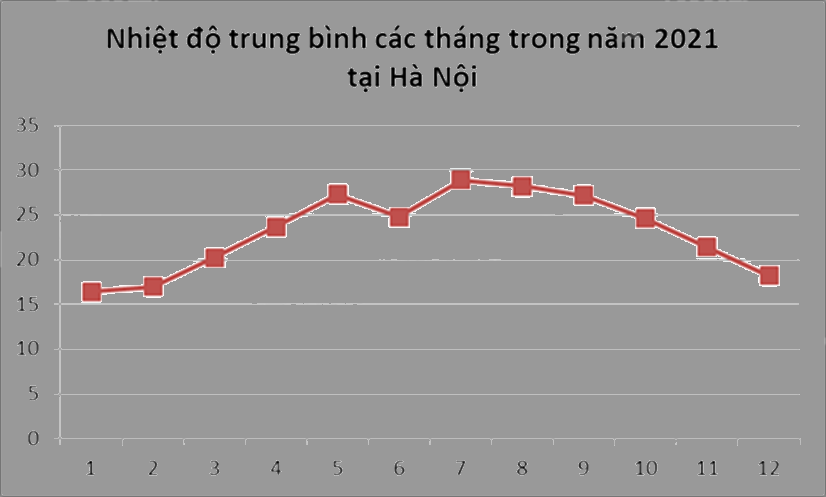
Tháng 1.
Tháng 5.
Tháng 7.
Tháng 8.
Đáp án : C
Quan sát biểu đồ, vị trí nào cao nhất thì tháng đó có nhiệt độ cao nhất.
Quan sát biểu đồ ta thấy điểm biểu diễn ở vị trí tháng 7 là cao nhất nên nhiệt độ trung bình tháng 7 cao nhất.
Đáp án C
Cho \(\Delta MNP = \Delta DHK\). Khẳng định nào sau đây là đúng:
NP = DH.
MN = DK.
\(\widehat {MPN} = \widehat {HDK}\).
\(\widehat {MNP} = \widehat {DHK}\).
Đáp án : D
Hai tam giác bằng nhau thì các cạnh và các góc tương ứng của chúng bằng nhau.
Vì \(\Delta MNP = \Delta DHK\) nên ta có: \(MN = DH;MP = DK;NP = HK\); \(\widehat M = \widehat D;\widehat N = \widehat H;\widehat P = \widehat K\).
Do đó A sai; B sai; C sai; D đúng.
Đáp án D
Cho tam giác ABC cân tại A, khẳng định nào sau đây SAI?
AB = BC.
AB = AC.
\(\widehat B = \widehat C\).
\(\widehat B = \frac{{180^\circ - \widehat A}}{2}\).
Đáp án : A
Tam giác cân thì hai cạnh bên bằng nhau và hai góc kề đáy bằng nhau.
Tổng ba góc của một tam giác là \(180^\circ \).
Tam giác ABC cân tại A thì \(\widehat B = \widehat C\); \(AB = AC\) nên khẳng định B, C đúng.
Tam giác ABC có \(\widehat A + \widehat B + \widehat C = 180^\circ \), \(\widehat B = \widehat C\) nên \(\widehat A + 2\widehat B = 180^\circ \),
suy ra \(2\widehat B = 180^\circ - \widehat A\),
do đó \(\widehat B = \frac{{180^\circ - \widehat A}}{2}\) nên khẳng định D đúng.
Đáp án A
Thực hiện phép tính:
a) \( - 0,5 + \frac{3}{4}\)
b) \({\left( { - \frac{2}{3}} \right)^2}.\frac{9}{{16}} + \sqrt {\frac{4}{{81}}} :\frac{{16}}{9} - \left| { - \frac{9}{{16}}} \right|.\frac{2}{3}\)
Áp dụng quy tắc cộng, trừ, nhân, chia với số thực.
b) Sử dụng kiến thức về bình phương của một số, căn bậc hai số học và giá trị tuyệt đối của một số thực.
a) \( - 0,5 + \frac{3}{4} = - \frac{1}{2} + \frac{3}{4} = \frac{{ - 2 + 3}}{4} = \frac{1}{4}\).
b) \({\left( { - \frac{2}{3}} \right)^2}.\frac{9}{{16}} + \sqrt {\frac{4}{{81}}} :\frac{{16}}{9} - \left| { - \frac{9}{{16}}} \right|.\frac{2}{3}\)
\(\begin{array}{l} = \frac{4}{9}.\frac{9}{{16}} + \frac{2}{9}.\frac{9}{{16}} - \frac{9}{{16}}.\frac{2}{3}\\ = \frac{9}{{16}}.\left( {\frac{4}{9} + \frac{2}{9} - \frac{2}{3}} \right)\\ = \frac{9}{{16}}.0 = 0\end{array}\)
Tìm \(x\), biết:
a) \(\frac{4}{3} + x = \frac{{ - 1}}{6}\)
b) \(2\left| {\frac{4}{5} - 2x} \right| + \frac{3}{5} = 3\)
Kết hợp chuyển vế và thực hiện phép tính để tìm x.
b) Ta cần chia hai trường hợp: \(\left| A \right| = B\) thì A = B hoặc A = -B.
a) \(\frac{4}{3} + x = \frac{{ - 1}}{6}\)
\(\begin{array}{l}x = \frac{{ - 1}}{6} - \frac{4}{3}\\x = \frac{{ - 1 - 8}}{6}\\x = \frac{{ - 3}}{2}\end{array}\)
Vậy \(x = \frac{{ - 3}}{2}\).
b) \(2\left| {\frac{4}{5} - 2x} \right| + \frac{3}{5} = 3\)
\(\begin{array}{l}2\left| {\frac{4}{5} - 2x} \right| = 3 - \frac{3}{5}\\2\left| {\frac{4}{5} - 2x} \right| = \frac{{12}}{5}\\\left| {\frac{4}{5} - 2x} \right| = \frac{{12}}{5}:2\\\left| {\frac{4}{5} - 2x} \right| = \frac{6}{5}\\\frac{4}{5} - 2x = \pm \frac{6}{5}\end{array}\)
+) TH1: \(\frac{4}{5} - 2x = \frac{6}{5}\)
\(\begin{array}{l}2x = \frac{4}{5} - \frac{6}{5}\\2x = \frac{{ - 2}}{5}\\x = \frac{{ - 2}}{5}:2\\x = \frac{{ - 1}}{5}\end{array}\)
+) TH2: \(\frac{4}{5} - 2x = - \frac{6}{5}\)
\(\begin{array}{l}2x = \frac{4}{5} + \frac{6}{5}\\2x = 2\\x = 2:2\\x = 1\end{array}\)
Vậy \(x \in \left\{ {\frac{{ - 1}}{5};1} \right\}\)
Tỉ lệ phần trăm học sinh của khối 7 thích chơi các môn thể thao được thống kê theo bảng sau:

a) Hãy vẽ biểu đồ hình quạt tròn.
b) Biết số học sinh khối 7 là 320 học sinh. Tính số học sinh thích chơi đá cầu.
a) Cách vẽ biểu đồ hình quạt tròn:
+ Vẽ 1 đường tròn
+ Tính số đo góc của hình quạt biểu diễn từng đối tượng: 1% tương ứng với 3,6 độ.
+ Đo góc và chia hình tròn thành các hình quạt có số đo tương ứng
+ Điền số phần trăm tương ứng vào từng hình quạt, tô màu và viết chú thích, đặt tên cho biểu đồ.
b) Tính m% của một số a theo công thức: \(m\% .a\).
a) Số đo góc của hình quạt biểu diễn từng đối tượng là:

Ta được biểu đồ hình quạt tròn như sau:
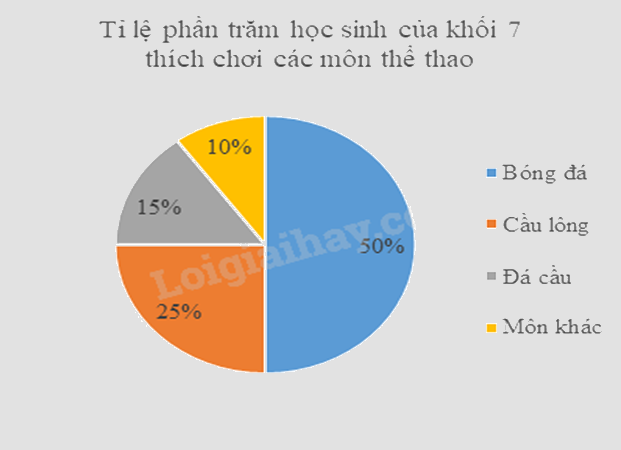
b) Số học sinh thích chơi đá cầu là: \(15\% .320 = 48\) (học sinh)
Cho tam giác ABC nhọn có AB = AC. Gọi M là trung điểm của đoạn thẳng BC.
a) Chứng minh \(\Delta ABM = \Delta ACM\).
b) Chứng minh \(AM \bot BC\).
c) Trên tia đối của tia MA lấy điểm E sao cho \(MA = ME\). Kẻ \(BH \bot AC\) tại H, \(CK \bot BE\) tại K. Chứng minh \(AC//BE\) và M là trung điểm của đoạn thẳng HK.
a) Chứng minh \(\Delta ABM = \Delta ACM\) theo trường hợp cạnh cạnh cạnh.
b) Từ \(\Delta ABM = \Delta ACM\) suy ra \(\widehat {AMB} = \widehat {AMC}\) và hai góc này là hai góc kề bù suy ra \(AM \bot BC\).
c) Chứng minh \(\Delta AMC = \Delta EMB\) nên \(\widehat {ACM} = \widehat {EBM}\), suy ra AC // BE.
Chứng minh MH = MK và H, M, K thẳng hàng nên M là trung điểm của HK.
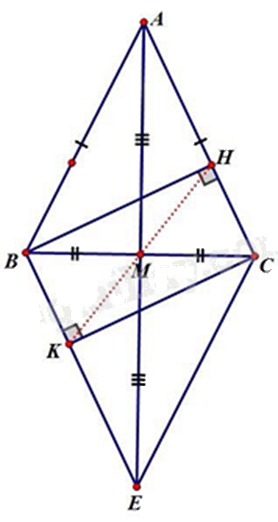
a) Xét \(\Delta ABM\) và \(\Delta ACM\) có:
AB = AC (gt)
BM = CM (M là trung điểm của BC)
AM chung
Suy ra \(\Delta ABM = \Delta ACM\) (c.c.c)
b) Vì \(\Delta ABM = \Delta ACM\) nên \(\widehat {AMB} = \widehat {AMC}\) (hai góc tương ứng).
Mà hai góc này là hai góc kề bù nên \(\widehat {AMB} + \widehat {AMC} = 180^\circ \)
Suy ra \(\widehat {AMB} + \widehat {AMB} = 180^\circ \), do đó \(\widehat {AMB} = 90^\circ \) hay \(AM \bot BC\).
c) +) Xét \(\Delta AMC\) và \(\Delta EMB\) có:
MA = ME (gt)
\(\widehat {AMC} = \widehat {EMB}\left( { = 90^\circ } \right)\)
\(BM = CM\)
Suy ra \(\Delta AMC = \Delta EMB\) (hai cạnh góc vuông)
nên \(\widehat {ACM} = \widehat {EBM}\) (hai góc tương ứng).
Mà hai góc này ở vị trí so le trong nên AC // BE.
+) Xét \(\Delta BHC\) và \(\Delta CKB\) có:
\(\widehat {BHC} = \widehat {CKB}\left( { = 90^\circ } \right)\)
\(\widehat {HCB} = \widehat {KBC}\) (cmt)
BC chung
suy ra \(\Delta BHC = \Delta CKB\) (cạnh huyền – góc nhọn)
suy ra \(BH = CK;\widehat {HBC} = \widehat {KCB}\) (hai cạnh và hai góc tương ứng)
Xét \(\Delta BMH\) và \(\Delta CMK\) có:
\(BH = CK\) (cmt)
\(\widehat {HBM} = \widehat {KCM}\) (cmt)
\(BM = CM\)
Suy ra \(\Delta BMH = \Delta CMK\) (c.g.c)
Do đó MH = MK (1) và \(\widehat {BMH} = \widehat {CMK}\)(hai cạnh và hai góc tương ứng)
Mà \(\widehat {BMH} + \widehat {HMC} = 180^\circ \) (hai góc kề bù) nên \(\widehat {CMK} + \widehat {HMC} = 180^\circ \), do đó H, M, K thẳng hàng. (2)
Từ (1) và (2) suy ra M là trung điểm của HK.
Cho \(A = \frac{1}{3} + \frac{1}{{{3^3}}} + \frac{1}{{{3^5}}} + \frac{1}{{{3^7}}} + ... + \frac{1}{{{3^{2023}}}}\). Chứng minh rằng \(A < \frac{3}{8}\).
Tính 9A.
Xét 9A – A.
Từ đó chứng minh được \(A < \frac{3}{8}\).
Ta có:
\(\begin{array}{c}9A = 9\left( {\frac{1}{3} + \frac{1}{{{3^3}}} + \frac{1}{{{3^5}}} + \frac{1}{{{3^7}}} + ... + \frac{1}{{{3^{2023}}}}} \right)\\ = 3 + \frac{1}{3} + \frac{1}{{{3^3}}} + \frac{1}{{{3^5}}} + ... + \frac{1}{{{3^{2021}}}}\end{array}\)
Xét \(9A - A = \left( {3 + \frac{1}{3} + \frac{1}{{{3^3}}} + \frac{1}{{{3^5}}} + ... + \frac{1}{{{3^{2021}}}}} \right) - \left( {\frac{1}{3} + \frac{1}{{{3^3}}} + \frac{1}{{{3^5}}} + \frac{1}{{{3^7}}} + ... + \frac{1}{{{3^{2023}}}}} \right)\)
\(\begin{array}{c}8A = 3 + \frac{1}{3} + \frac{1}{{{3^3}}} + \frac{1}{{{3^5}}} + ... + \frac{1}{{{3^{2021}}}} - \frac{1}{3} - \frac{1}{{{3^3}}} - \frac{1}{{{3^5}}} - \frac{1}{{{3^7}}} - ... - \frac{1}{{{3^{2023}}}}\\8A = 3 + \left( {\frac{1}{3} - \frac{1}{3}} \right) + \left( {\frac{1}{{{3^3}}} - \frac{1}{{{3^3}}}} \right) + ... + \left( {\frac{1}{{{3^{2021}}}} - \frac{1}{{{3^{2021}}}}} \right) - \frac{1}{{{3^{2023}}}}\end{array}\)
\(8A = 3 - \frac{1}{{{3^{2023}}}}\)
\(A = \frac{3}{8} - \frac{1}{{{{8.3}^{2023}}}}\)
Vì \(\frac{1}{{{{8.3}^{2023}}}} > 0\) nên \(A = \frac{3}{8} - \frac{1}{{{{8.3}^{2023}}}} < \frac{3}{8}\)
Vậy \(A < \frac{3}{8}\)
Đề thi học kì 1 Toán 7 Kết nối tri thức - Đề số 16 là một phần quan trọng trong quá trình đánh giá năng lực học tập của học sinh sau một học kì. Đề thi này không chỉ kiểm tra kiến thức đã học mà còn đánh giá khả năng vận dụng kiến thức vào giải quyết các bài toán thực tế. Bài viết này sẽ cung cấp một cái nhìn tổng quan về đề thi, phân tích cấu trúc, và hướng dẫn giải chi tiết từng câu hỏi, giúp học sinh ôn tập hiệu quả và tự tin bước vào kỳ thi.
Đề thi thường bao gồm các dạng bài sau:
Tỷ lệ phân bổ điểm giữa phần trắc nghiệm và phần tự luận có thể khác nhau tùy theo quy định của từng trường. Tuy nhiên, phần tự luận thường chiếm tỷ lệ cao hơn, đòi hỏi học sinh phải có khả năng giải quyết vấn đề và trình bày lời giải một cách logic và rõ ràng.
Các chủ đề chính thường xuất hiện trong đề thi bao gồm:
Để giúp học sinh ôn tập hiệu quả, chúng ta sẽ đi vào giải chi tiết một số câu hỏi tiêu biểu trong đề thi:
Cho hai số hữu tỉ a = -2/3 và b = 1/2. Tính a + b.
Giải: a + b = -2/3 + 1/2 = -4/6 + 3/6 = -1/6
Giải phương trình: 2x - 5 = 3
Giải: 2x - 5 = 3 => 2x = 8 => x = 4
Cho tam giác ABC vuông tại A. Biết AB = 3cm, AC = 4cm. Tính độ dài cạnh BC.
Giải: Áp dụng định lý Pitago vào tam giác ABC vuông tại A, ta có: BC2 = AB2 + AC2 = 32 + 42 = 9 + 16 = 25 => BC = 5cm
Để nâng cao kiến thức và kỹ năng giải toán, học sinh có thể tham khảo thêm các tài liệu sau:
Việc luyện tập thường xuyên với các đề thi thử và bài tập khác nhau sẽ giúp học sinh làm quen với các dạng bài và rèn luyện kỹ năng giải quyết vấn đề một cách hiệu quả.
Đề thi học kì 1 Toán 7 Kết nối tri thức - Đề số 16 là một cơ hội để học sinh đánh giá năng lực học tập của mình và chuẩn bị cho các kỳ thi tiếp theo. Hy vọng rằng với những hướng dẫn chi tiết và lời khuyên trên, các em sẽ tự tin và đạt kết quả tốt nhất trong kỳ thi sắp tới.