Chào mừng các em học sinh lớp 7 đến với đề thi giữa kì 2 môn Toán chương trình Kết nối tri thức - Đề số 9.
Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong học kì 2.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán!
Thay tỉ số 1,2 : 1,35 bằng tỉ số giữa các số nguyên ta được:
Biết \(\frac{x}{2} = \frac{y}{3}\) và \(x + y = - 15\). Khi đó giá trị của x, y là
Biết đại lượng y tỉ lệ thuận với đại lượng x với các cặp giá trị tương ứng trong bảng sau:

Giá trị cần điền vào “?” là
Cho biết y tỉ lệ nghịch với x theo hệ số tỉ lệ a và khi \(x = - 2\) thì \(y = 4\). Khi đó, hệ số a bằng bao nhiêu?
Bộ ba độ dài đoạn thẳng nào sau đây tạo thành một tam giác?
Biểu thức đại số biểu thị tích của hai số tự nhiên liên tiếp là:
Trong các biểu thức sau, em hãy chỉ ra biểu thức số.
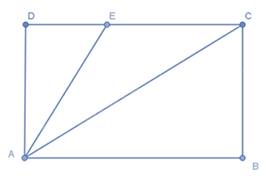
Cho ABCD là hình chữ nhật như hình vẽ, điểm E nằm trên cạnh CD. Khẳng định nào sau đây là sai?
Điền vào chỗ trống sau: “Đường thẳng vuông góc với một đoạn thẳng tại … của nó được gọi là đường trung trực của đoạn thẳng đó”.
Biết y tỉ lệ thuận với x theo hệ số tỉ lệ k = 2. Khi x = –3 thì giá trị của y bằng bao nhiêu?
Cho x và y là hai đại lượng tỉ lệ nghịch với nhau và khi x = –12 thì y = 8. Khi x = 3 thì y bằng
Giá trị của biểu thức \(A = 2{x^2} - 3x + 1\) tại \(x = - 1\) là
Tìm số hữu tỉ x trong các tỉ lệ thức sau:
a) \(\frac{{ - 6}}{x} = \frac{9}{{ - 15}}\)
b) \(\frac{{ - 4}}{x} = \frac{x}{{ - 49}}\)
a) Cho \(\frac{a}{b} = \frac{6}{5}\). Tìm a, b biết: a – b = 3
b) Cho \(\frac{x}{2} = \frac{y}{3} = \frac{z}{5}\). Tìm x, y, z biết \(x - y + z = 32\)
Ba đơn vị cùng vận chuyển 700 tấn hàng. Đơn vị A có 10 xe trọng tải mỗi xe là 5 tấn; đơn vị B có 20 xe trọng tải mỗi xe là 4 tấn; đơn vị C có 14 xe trọng tải mỗi xe là 5 tấn. Hỏi mỗi đơn vị vận chuyển được bao nhiêu tấn hàng, biết mỗi xe đều chở một số chuyến như nhau?
Cho góc xOy khác góc bẹt có Ot là tia phân giác. Qua điểm H thuộc tia Ot, kẻ đường vuông góc với Ot và cắt Ox và Oy theo thứ tự A và B.
a) Chứng minh OA = OB.
b) Lấy điểm C nằm giữa O và H. Chứng minh \(\widehat {ACH} = \widehat {HCB}\).
c) AC cắt Oy ở D. Trên tia Ox lấy điểm E sao cho OE = OD. Chứng minh ba điểm B, C, E thẳng hàng.
Cho tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\). Chứng minh: \(\frac{{ab}}{{cd}} = \frac{{{a^2} - {b^2}}}{{{c^2} - {d^2}}}\).
Thay tỉ số 1,2 : 1,35 bằng tỉ số giữa các số nguyên ta được:
Đáp án : B
Dựa vào kiến thức về tỉ lệ thức.
Ta có: \(1,2:1,35 = \frac{{1,2}}{{1,35}} = \frac{8}{9} = 8:9\).
Biết \(\frac{x}{2} = \frac{y}{3}\) và \(x + y = - 15\). Khi đó giá trị của x, y là
Đáp án : D
Dựa vào tính chất dãy tỉ số bằng nhau.
Ta có: \(\frac{x}{2} = \frac{y}{3} = \frac{{x + y}}{{2 + 3}} = \frac{{ - 15}}{5} = - 3\) (tính chất dãy tỉ số bằng nhau)
Suy ra \(x = - 3.2 = - 6;y = - 3.3 = - 9\).
Biết đại lượng y tỉ lệ thuận với đại lượng x với các cặp giá trị tương ứng trong bảng sau:

Giá trị cần điền vào “?” là
Đáp án : A
Dựa vào kiến thức về hai đại lượng tỉ lệ thuận.
Vì y tỉ lệ thuận với x nên \(k = \frac{y}{x} = \frac{{ - 5}}{1} = - 5 = \frac{1}{?}\) suy ra \(? = 1:\left( { - 5} \right) = \frac{{ - 1}}{5}\).
Cho biết y tỉ lệ nghịch với x theo hệ số tỉ lệ a và khi \(x = - 2\) thì \(y = 4\). Khi đó, hệ số a bằng bao nhiêu?
Đáp án : C
Dựa vào kiến thức về hai đại lượng tỉ lệ nghịch.
Vì y tỉ lệ nghịch với x theo hệ số tỉ lệ a nên \(a = xy = \left( { - 2} \right).4 = - 8\).
Bộ ba độ dài đoạn thẳng nào sau đây tạo thành một tam giác?
Đáp án : B
Dựa vào quan hệ giữa ba cạnh của một tam giác.
Ta có: 5 – 4 = 1 nên 5cm; 4cm; 1cm không thể tạo thành một tam giác.
3cm; 4cm; 5cm có thể tạo thành một tam giác nên ta chọn đáp án B.
2 + 2 = 4 < 5 nên 5cm; 2cm; 2cm không thể tạo thành một tam giác.
1 + 4 = 5 < 10 nên 1cm; 4cm; 10cm không thể tạo thành một tam giác.
Biểu thức đại số biểu thị tích của hai số tự nhiên liên tiếp là:
Đáp án : B
Dựa vào kiến thức về biểu thức đại số.
Vì x và y là hai số tự nhiên bất kì nên \(xy\) không biểu thị tích của hai số tự nhiên liên tiếp.
Vì x và x + 1 là hai số tự nhiên liên tiếp nên \(x.\left( {x + 1} \right)\)với \(x \in {\rm N}\) là biểu thức biểu thị tích của hai số tự nhiên liên tiếp.
Vì x và y là hai số tự nhiên bất kì nên \(x.\left( {y + 1} \right)\) không biểu thị tích của hai số tự nhiên liên tiếp.
Vì x và y là hai số tự nhiên bất kì nên \(\left( {x + 1} \right)\left( {y + 1} \right)\) không biểu thị tích của hai số tự nhiên liên tiếp.
Trong các biểu thức sau, em hãy chỉ ra biểu thức số.
Đáp án : D
Dựa vào kiến thức về biểu thức số.
Trong các biểu thức trên, chỉ có \(\frac{{3.(4 + 5)}}{2}\) là biểu thức số.
Cho ABCD là hình chữ nhật như hình vẽ, điểm E nằm trên cạnh CD. Khẳng định nào sau đây là sai?
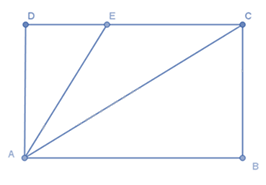
Đáp án : A
Dựa vào quan hệ giữa đường xiên và hình chiếu.
Xét tam giác vuông ACD có AD < AC (trong tam giác vuông, cạnh huyền là cạnh lớn nhất)
Vì E nằm trên cạnh CD nên DE < DC suy ra AE < AC (quan hệ giữa đường vuông góc và đường xiên.
Suy ra AD < AE < AC nên A sai.
Điền vào chỗ trống sau: “Đường thẳng vuông góc với một đoạn thẳng tại … của nó được gọi là đường trung trực của đoạn thẳng đó”.
Đáp án : D
Dựa vào khái niệm về đường trung trực của đoạn thẳng.
“Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó”.
Biết y tỉ lệ thuận với x theo hệ số tỉ lệ k = 2. Khi x = –3 thì giá trị của y bằng bao nhiêu?
Đáp án : A
Dựa vào kiến thức về hai đại lượng tỉ lệ thuận.
Vì y tỉ lệ thuận với x theo hệ số tỉ lệ k = 2 nên \(y = 2x\).
Thay \(x = - 3\) vào công thức ta được: \(y = 2.\left( { - 3} \right) = - 6\).
Cho x và y là hai đại lượng tỉ lệ nghịch với nhau và khi x = –12 thì y = 8. Khi x = 3 thì y bằng
Đáp án : A
Dựa vào kiến thức về hai đại lượng tỉ lệ nghịch.
Vì hai đại lượng x và y là hai đại lượng tỉ lệ nghịch với nhau nên \(a = - 12.8 = - 96\).
Thay \(x = 3\) vào công thức ta được: \( - 96 = 3.y\) suy ra \(y = - 32\).
Giá trị của biểu thức \(A = 2{x^2} - 3x + 1\) tại \(x = - 1\) là
Đáp án : A
Thay giá trị của x vào biểu thức để tính giá trị của biểu thức.
Thay x = -1 vào A, ta được:
\(A = 2.{\left( { - 1} \right)^2} - 3.\left( { - 1} \right) + 1 = 6\).
Tìm số hữu tỉ x trong các tỉ lệ thức sau:
a) \(\frac{{ - 6}}{x} = \frac{9}{{ - 15}}\)
b) \(\frac{{ - 4}}{x} = \frac{x}{{ - 49}}\)
Áp dụng tính chất của tỉ lệ thức.
a) Ta có: \(\frac{{ - 6}}{x} = \frac{9}{{ - 15}}\)
Suy ra \(\left( { - 6} \right).\left( { - 15} \right) = 9.x\)
\(x = \frac{{\left( { - 6} \right).\left( { - 15} \right)}}{9} = 10\)
Vậy x = 10.
b) Ta có: \(\frac{{ - 4}}{x} = \frac{x}{{ - 49}}\)
Suy ra \(\left( { - 4} \right)\left( { - 49} \right) = x.x\)
\(\begin{array}{l}{x^2} = 196\\x = \pm 14\end{array}\)
Vậy \(x = \pm 14\).
a) Cho \(\frac{a}{b} = \frac{6}{5}\). Tìm a, b biết: a – b = 3
b) Cho \(\frac{x}{2} = \frac{y}{3} = \frac{z}{5}\). Tìm x, y, z biết \(x - y + z = 32\)
Áp dụng tính chất của dãy tỉ số bằng nhau.
a) Ta có: \(\frac{a}{b} = \frac{6}{5}\) suy ra \(\frac{a}{6} = \frac{b}{5}\).
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{6} = \frac{b}{5} = \frac{{a - b}}{{6 - 5}} = \frac{3}{1} = 3\).
Suy ra \(a = 3.6 = 18\); \(b = 3.5 = 15\).
Vậy a = 16; b = 15.
b) Ta có: \(\frac{x}{2} = \frac{y}{3} = \frac{z}{5}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{2} = \frac{y}{3} = \frac{z}{5} = \frac{{x - y + z}}{{2 - 3 + 5}} = \frac{{32}}{4} = 8\).
Suy ra \(x = 8.2 = 16\)
\(\begin{array}{l}y = 8.3 = 24\\z = 8.5 = 40\end{array}\)
Vậy \(x = 16;y = 24;z = 40\).
Ba đơn vị cùng vận chuyển 700 tấn hàng. Đơn vị A có 10 xe trọng tải mỗi xe là 5 tấn; đơn vị B có 20 xe trọng tải mỗi xe là 4 tấn; đơn vị C có 14 xe trọng tải mỗi xe là 5 tấn. Hỏi mỗi đơn vị vận chuyển được bao nhiêu tấn hàng, biết mỗi xe đều chở một số chuyến như nhau?
Dựa vào tính chất của dãy tỉ số bằng nhau.
Gọi x, y, z (tấn)lần lượt là khối lượng hàng các đơn vị A, B, C vận chuyển (x, y, z > 0).
Theo đề bài ta suy ra: \(\frac{x}{{50}} = \frac{y}{{80}} = \frac{z}{{70}}\) và \(x + y + z = 700\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\begin{array}{l}\frac{x}{{50}} = \frac{y}{{80}} = \frac{z}{{70}} = \frac{{x + y + z}}{{50 + 80 + 70}} = \frac{{700}}{{200}} = 3,5\\x = 175;\quad y = 280;\quad z = 245\end{array}\)
Vậy khối lượng hàng các đơn vị A, B, C vận chuyển lần lượt là 175; 280; 245 tấn.
Cho góc xOy khác góc bẹt có Ot là tia phân giác. Qua điểm H thuộc tia Ot, kẻ đường vuông góc với Ot và cắt Ox và Oy theo thứ tự A và B.
a) Chứng minh OA = OB.
b) Lấy điểm C nằm giữa O và H. Chứng minh \(\widehat {ACH} = \widehat {HCB}\).
c) AC cắt Oy ở D. Trên tia Ox lấy điểm E sao cho OE = OD. Chứng minh ba điểm B, C, E thẳng hàng.
a) Chứng minh được: ∆AHO = ∆BHO (góc – cạnh – góc)
Suy ra OA = OB (hai cạnh tương ứng)
b) Chứng minh được: ∆AHC = ∆BHC (hai cạnh góc vuông)
Suy ra \(\widehat {ACH} = \widehat {HCB}\) (hai góc tương ứng)
c) Chứng minh được: ∆OEC = ∆ODC (c.g.c)
Chứng minh được: \(\widehat {ECO} + \widehat {OCD} + \widehat {BCD} = {180^0}\)
Suy ra ba điểm E, C, B thẳng hàng.
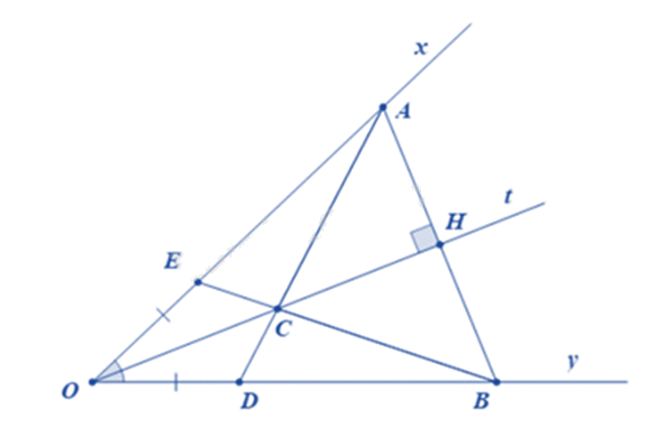
a) Xét tam giác AHO và tam giác BHO có:
\(\widehat {AOH} = \widehat {BOH}\) (Ot là tia phân giác của \(\widehat {AOB}\))
OH chung
\(\widehat {AHO} = \widehat {BHO}\left( { = {{90}^0}} \right)\)
Suy ra \(\Delta AHO = \Delta BHO\left( {g.c.g} \right)\)
Suy ra OA = OB (hai cạnh tương ứng) (đpcm)
b) \(\Delta AHO = \Delta BHO\) suy ra AH = HB (hai cạnh tương ứng)
Xét tam giác AHC và tam giác BHC có:
HC chung
\(\widehat {AHC} = \widehat {BHC}\left( { = {{90}^0}} \right)\)
AH = HB
Suy ra \(\Delta AHC = \Delta BHC\) (hai cạnh góc vuông)
Suy ra \(\widehat {ACH} = \widehat {HCB}\) (hai góc tương ứng)
c) Xét tam giác OCE và OCD có:
OE = OD
\(\widehat {EOC} = \widehat {DOC}\)
OC chung
Suy ra ∆OEC = ∆ODC (c.g.c)
Suy ra EC = DC (hai cạnh tương ứng)
Ta có OA = OB và OE = OD nên AE = BD.
Xét \(\Delta ECA\) và \(\Delta DCB\) có:
EC = ED (cmt)
EA = DB (cmt)
CA = CB (\(\Delta AHC = \Delta BHC\))
Suy ra \(\Delta ECA = \Delta DCB\) (c.c.c)
Suy ra \(\widehat {ECA} = \widehat {DCB}\) (hai góc tương ứng)
Mặt khác \(\widehat {ECA} + \widehat {ECD} = {180^0}\) (vì AC cắt Oy tại D)
Suy ra \(\widehat {DCB} + \widehat {ECD} = {180^0}\) hay B, C, E thẳng hàng (đpcm).
Cho tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\). Chứng minh: \(\frac{{ab}}{{cd}} = \frac{{{a^2} - {b^2}}}{{{c^2} - {d^2}}}\).
Đặt \(\frac{a}{b} = \frac{c}{d} = k\).
Áp dụng dãy tỉ số bằng nhau để chứng minh.
Đặt \(\frac{a}{b} = \frac{c}{d} = k \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = bk}\\{c = dk}\end{array}} \right.\)
Do đó ta có:
\(\frac{{ac}}{{bd}} = \frac{{bkdk}}{{bd}} = {k^2}(1)\)
Ta cũng có:
\(\frac{{{a^2} + {c^2}}}{{{b^2} + {d^2}}} = \frac{{{{(bk)}^2} + {{(dk)}^2}}}{{{b^2} + {d^2}}} = \frac{{{b^2}{k^2} + {d^2}{k^2}}}{{{b^2} + {d^2}}} = \frac{{{k^2}\left( {{b^2} + {d^2}} \right)}}{{{b^2} + {d^2}}} = {k^2}(2)\)
Từ (1) và (2) suy ra:
\(\frac{{ac}}{{bd}} = \frac{{{a^2} + {c^2}}}{{{b^2} + {d^2}}} = \left( {{k^2}} \right)\) (đpcm)
Đề thi giữa kì 2 Toán 7 Kết nối tri thức - Đề số 9 là một bài kiểm tra quan trọng giúp học sinh đánh giá mức độ nắm vững kiến thức đã học trong học kì. Đề thi bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính như biểu thức đại số, phương trình bậc nhất một ẩn, bất đẳng thức, và các ứng dụng thực tế của Toán học.
Thông thường, đề thi giữa kì 2 Toán 7 Kết nối tri thức - Đề số 9 sẽ có cấu trúc tương tự như sau:
Để chuẩn bị tốt nhất cho đề thi giữa kì 2 Toán 7 Kết nối tri thức - Đề số 9, học sinh cần nắm vững các chủ đề sau:
Để đạt kết quả tốt nhất trong đề thi giữa kì 2 Toán 7 Kết nối tri thức - Đề số 9, học sinh cần:
Bài toán: Giải phương trình sau: 2x + 5 = 11
Giải:
Kết luận: Phương trình có nghiệm x = 3
Để hỗ trợ học sinh ôn tập và luyện thi hiệu quả, giaitoan.edu.vn cung cấp:
Hãy dành thời gian ôn tập và luyện thi một cách nghiêm túc. Đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè nếu gặp khó khăn. Chúc các em học sinh đạt kết quả tốt nhất trong đề thi giữa kì 2 Toán 7 Kết nối tri thức - Đề số 9!