Chào mừng các em học sinh lớp 7 đến với đề thi học kì 2 môn Toán - Đề số 4, chương trình Kết nối tri thức.
Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong học kì 2, chuẩn bị tốt nhất cho kỳ thi sắp tới.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán!
I. TRẮC NGHIỆM ( 2 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
I. TRẮC NGHIỆM ( 2 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1. Hai đại lượng \(x,y\) trong công thức nào tỉ lệ nghịch với nhau:
A. \(y = 5 + x\)
B. \(x = \dfrac{5}{y}\)
C. \(y = 5x\)
D. \(x = 5y\)
Câu 2. Trong các sự kiện, hiện tượng sau, đâu là biến cố chắc chắn?
A. Mặt Trời quay quanh Trái Đất
B. Khi gieo đồng xu thì được mặt ngửa
C. Có 9 cơn bão đổ bộ vào nước ta trong năm tới
D. Ngày mai, Mặt Trời mọc ở phía Đông
Câu 3. Một hình hộp chữ nhật được ghép bởi 42 hình lập phương cạnh \(1\,cm.\) Biết chu vi đáy của hình hộp chữ nhật là \(18\,cm.\) Khi đó tổng ba kích thước của hình hộp chữ nhật là:
A. \(12\,cm\)
B. \(15\,cm\)
C. \(10\,cm\
D. \(9\,cm\)
Câu 4. Biểu thức nào sau đây không là đơn thức?
A. \(4{x^2}y\left( { - 2x} \right)\)
B. \(2x\)
C. \(2xy - {x^2}\)
D. \(2021\)
Câu 5. Sắp xếp các hạng tử của đa thức \(P\left( x \right) = 2{x^3} - 7{x^2} + {x^4} - 4\) theo lũy thừa giảm dần của biến ta được:
A. \(P\left( x \right) = {x^4} + 2{x^3} - 7{x^2} - 4\)
B. \(P\left( x \right) = 7{x^2} + 2{x^3} + {x^4} - 4\)
C. \(P\left( x \right) = - 4 - 7{x^2} + 2{x^3} + {x^4}\)
D. \(P\left( x \right) = {x^4} - 2{x^3} - 7{x^2} - 4\)
Câu 6. Cho tam giác \(MNP\) có \(NP = 1cm,MP = 7cm\). Độ dài cạnh \(MN\) là một số nguyên (cm). Độ dài cạnh \(MN\) là:
A. \(8cm\)
B. \(5cm\)
C. \(6cm\)
D. \(7cm\)
Câu 7. Cho tam giác ABC có \(AB = AC.\) Trên các cạnh AB và AC lấy các điểm D,E sao cho \(AD = AE.\) Gọi \(K\) là giao điểm của BE và CD. Chọn câu sai.
A. \(BE = CD\)
B. \(BK = KC\)
C. \(BD = CE\)
D. \(DK = KC\)
Câu 8. Giao điểm của 3 đường trung trực của tam giác
A. cách đều 3 cạnh của tam giác.
B. được gọi là trực tâm của tam giác.
C. cách đều 3 đỉnh của tam giác.
D. cách đỉnh một đoạn bằng \(\dfrac{2}{3}\) độ dài đường trung tuyến đi qua đỉnh đó.
II. PHẦN TỰ LUẬN (8,0 điểm)
Bài 1. (1 điểm) Tìm \(x\) biết:
a) \(\dfrac{{5x - 2}}{3} = \dfrac{{ - 3}}{4}\)
b) \(\left( {{x^2} - \dfrac{1}{4}} \right).\left( {x + \dfrac{2}{5}} \right) = 0\)
Bài 2. (1,5 điểm) Ba lớp 7A, 7B, 7C cùng tham gia lao động trồng cây. Biết số cây ở lớp 7A, 7B, 7C được trồng tỉ lệ với các số \(3\,;\,5\,;\,8\) và hai lần số cây của lớp 7A cộng với \(4\) lần số cây lớp 7B trồng được nhiều hơn số cây lớp 7C trồng được là \(108\) cây. Tính số cây trồng được của mỗi lớp
Bài 3. (1,5 điểm) Cho hai đa thức: \(f\left( x \right) = {x^5} + {x^3} - 4x - {x^5} + 3x + 7\) và \(g\left( x \right) = 3{x^2} - {x^3} + 8x - 3{x^2} - 14\).
a) Thu gọn và sắp xếp hai đa thức \(f\left( x \right)\) và \(g\left( x \right)\) theo lũy thừa giảm dần của biến.
b) Tính \(f\left( x \right) + g\left( x \right)\) và tìm nghiệm của đa thức \(f\left( x \right) + g\left( x \right)\).
Bài 4. (3,5 điểm) Cho tam giác ABC vuông tại A.
a) Tia phân giác của góc B cắt cạnh AC ở D. Kẻ DE vuông góc với BC tại E.
Chứng minh rằng ΔABD = ΔEBD.
b) So sánh AD và DC.
c) Tia ED cắt BA tại G. Gọi I là trung điểm GC. Chứng minh rằng B, D, I thẳng hàng.
Bài 5. (0,5 điểm) Cho \(x;{\kern 1pt} y;{\kern 1pt} z\) tỉ lệ thuận với \(3;{\kern 1pt} \,4;\,{\kern 1pt} 5.\) Tính giá trị của biểu thức
\(A = 2024\left( {x - y} \right)\left( {y - z} \right) - 506.{\left( {\dfrac{{x + y + z}}{6}} \right)^2}\)
Tải về
I. TRẮC NGHIỆM ( 2 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1. Hai đại lượng \(x,y\) trong công thức nào tỉ lệ nghịch với nhau:
A. \(y = 5 + x\)
B. \(x = \dfrac{5}{y}\)
C. \(y = 5x\)
D. \(x = 5y\)
Câu 2. Trong các sự kiện, hiện tượng sau, đâu là biến cố chắc chắn?
A. Mặt Trời quay quanh Trái Đất
B. Khi gieo đồng xu thì được mặt ngửa
C. Có 9 cơn bão đổ bộ vào nước ta trong năm tới
D. Ngày mai, Mặt Trời mọc ở phía Đông
Câu 3. Một hình hộp chữ nhật được ghép bởi 42 hình lập phương cạnh \(1\,cm.\) Biết chu vi đáy của hình hộp chữ nhật là \(18\,cm.\) Khi đó tổng ba kích thước của hình hộp chữ nhật là:
A. \(12\,cm\)
B. \(15\,cm\)
C. \(10\,cm\
D. \(9\,cm\)
Câu 4. Biểu thức nào sau đây không là đơn thức?
A. \(4{x^2}y\left( { - 2x} \right)\)
B. \(2x\)
C. \(2xy - {x^2}\)
D. \(2021\)
Câu 5. Sắp xếp các hạng tử của đa thức \(P\left( x \right) = 2{x^3} - 7{x^2} + {x^4} - 4\) theo lũy thừa giảm dần của biến ta được:
A. \(P\left( x \right) = {x^4} + 2{x^3} - 7{x^2} - 4\)
B. \(P\left( x \right) = 7{x^2} + 2{x^3} + {x^4} - 4\)
C. \(P\left( x \right) = - 4 - 7{x^2} + 2{x^3} + {x^4}\)
D. \(P\left( x \right) = {x^4} - 2{x^3} - 7{x^2} - 4\)
Câu 6. Cho tam giác \(MNP\) có \(NP = 1cm,MP = 7cm\). Độ dài cạnh \(MN\) là một số nguyên (cm). Độ dài cạnh \(MN\) là:
A. \(8cm\)
B. \(5cm\)
C. \(6cm\)
D. \(7cm\)
Câu 7. Cho tam giác ABC có \(AB = AC.\) Trên các cạnh AB và AC lấy các điểm D,E sao cho \(AD = AE.\) Gọi \(K\) là giao điểm của BE và CD. Chọn câu sai.
A. \(BE = CD\)
B. \(BK = KC\)
C. \(BD = CE\)
D. \(DK = KC\)
Câu 8. Giao điểm của 3 đường trung trực của tam giác
A. cách đều 3 cạnh của tam giác.
B. được gọi là trực tâm của tam giác.
C. cách đều 3 đỉnh của tam giác.
D. cách đỉnh một đoạn bằng \(\dfrac{2}{3}\) độ dài đường trung tuyến đi qua đỉnh đó.
II. PHẦN TỰ LUẬN (8,0 điểm)
Bài 1. (1 điểm) Tìm \(x\) biết:
a) \(\dfrac{{5x - 2}}{3} = \dfrac{{ - 3}}{4}\)
b) \(\left( {{x^2} - \dfrac{1}{4}} \right).\left( {x + \dfrac{2}{5}} \right) = 0\)
Bài 2. (1,5 điểm) Ba lớp 7A, 7B, 7C cùng tham gia lao động trồng cây. Biết số cây ở lớp 7A, 7B, 7C được trồng tỉ lệ với các số \(3\,;\,5\,;\,8\) và hai lần số cây của lớp 7A cộng với \(4\) lần số cây lớp 7B trồng được nhiều hơn số cây lớp 7C trồng được là \(108\) cây. Tính số cây trồng được của mỗi lớp
Bài 3. (1,5 điểm) Cho hai đa thức: \(f\left( x \right) = {x^5} + {x^3} - 4x - {x^5} + 3x + 7\) và \(g\left( x \right) = 3{x^2} - {x^3} + 8x - 3{x^2} - 14\).
a) Thu gọn và sắp xếp hai đa thức \(f\left( x \right)\) và \(g\left( x \right)\) theo lũy thừa giảm dần của biến.
b) Tính \(f\left( x \right) + g\left( x \right)\) và tìm nghiệm của đa thức \(f\left( x \right) + g\left( x \right)\).
Bài 4. (3,5 điểm) Cho tam giác ABC vuông tại A.
a) Tia phân giác của góc B cắt cạnh AC ở D. Kẻ DE vuông góc với BC tại E.
Chứng minh rằng ΔABD = ΔEBD.
b) So sánh AD và DC.
c) Tia ED cắt BA tại G. Gọi I là trung điểm GC. Chứng minh rằng B, D, I thẳng hàng.
Bài 5. (0,5 điểm) Cho \(x;{\kern 1pt} y;{\kern 1pt} z\) tỉ lệ thuận với \(3;{\kern 1pt} \,4;\,{\kern 1pt} 5.\) Tính giá trị của biểu thức
\(A = 2024\left( {x - y} \right)\left( {y - z} \right) - 506.{\left( {\dfrac{{x + y + z}}{6}} \right)^2}\)
I. Trắc nghiệm
1. B | 2. D | 3. A | 4. C |
5. A | 6. D | 7. D | 8. C |
Câu 1.
Phương pháp:
Vận dụng định nghĩa về đại lượng tỉ lệ nghịch.
Cách giải:
Ta có: \(x = \dfrac{5}{y}\) là hai đại lượng tỉ lệ nghịch với nhau.
Chọn B.
Câu 2.
Phương pháp:
Biến cố chắc chắn: Là biến cố biết trước được luôn xảy ra
Cách giải:
Đáp án ABiến cố không thể
Đáp án BBiến cố ngẫu nhiên
Đáp án CBiến cố ngẫu nhiên
Đáp án DMặt Trời luôn mọc ở phía Đông nên sự kiện “Ngày mai, Mặt Trời mọc ở phía Đông." Luôn xảy ra nên là biến
cố chắc chắn.
Chọn D.
Câu 3.
Phương pháp:
Áp dụng công thức tính tính chu vi hình chữ nhật và công thức tính thể tích hình hộp chữ nhật.
Cách giải:
Gọi độ dài các cạnh đáy của hình hộp chữ nhật là \(a\) và \(b,\) chiều cao là \(c\,\,\,\left( {a,b,c \in {\mathbb{N}^*}} \right).\)
Vì chu vi đáy của hình hộp chữ nhật là \(18\,cm\) nên ta có: \(2\left( {a + b} \right) = 18 \Rightarrow a + b = \dfrac{{18}}{2} = 9\,\,\,\,\left( 1 \right)\)
Thể tích khối lập phương cạnh \(1cm\) là: \({V_1} = {1^3} = 1\left( {c{m^3}} \right)\)
Thể tích của hình hộp chữ nhật là: \(V = 42.1 = 42\left( {c{m^3}} \right)\) \( \Rightarrow abc = 42\,\,\,\left( 2 \right)\)
Từ \(\left( 1 \right),\left( 2 \right) \Rightarrow \)\(a,\,b\) là ước của \(42\) và nhỏ hơn \(9.\)
+ Nếu các cạnh đáy là \(5\) và \(4\) thì \(c = \dfrac{{42}}{{a.b}} = \dfrac{{42}}{{5.4}} = \dfrac{{21}}{{10}}\,\) không là số tự nhiên
+ Nếu các cạnh đáy là \(6\) và \(3\) thì \(c = \dfrac{{42}}{{a.b}} = \dfrac{{42}}{{6.3}} = \dfrac{7}{3}\,\) không là số tự nhiên
+ Nếu các cạnh đáy là \(7\) và \(2\) thì \(c = \dfrac{{42}}{{a.b}} = \dfrac{{42}}{{7.2}} = 3\,\left( {TM} \right)\,\)
Vậy các cạnh của hình chữ nhật là \(7cm;\,2cm;\,3cm\) nên tổng ba kích thước của hình hộp chữ nhật là \(12cm.\)
Chọn A.
Câu 4.
Phương pháp:
Đơn thức là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và các biến.
Cách giải:
Biểu thức: \(2xy - {x^2}\) không là một đơn thức.
Chọn C.
Câu 5.
Phương pháp:
Thu gọn đa thức bằng cách nhóm các hạng tử đồng dạng lại rồi thu gọn chúng. Sau đó sắp xếp theo lũy thừa giảm dần của biến.
Cách giải:
Sắp xếp theo lũy thừa giảm dần của biến: \(P\left( x \right) = {x^4} + 2{x^3} - 7{x^2} - 4\)
Chọn A.
Câu 6.
Phương pháp:
Sử dụng hệ quả của bất đẳng thức trong tam giác:
+ Tồn tại một tam giác có độ dài ba cạnh là \(a,b,c\) nếu \(\left| {b - c} \right| < a < b + c\).
+ Trong trường hợp xác định được \(a\) là số lớn nhất trong ba số \(a,b,c\) thì điều kiện tồn tại tam giác là \(a < b + c\).
Cách giải:
Xét tam giác \(MNP\), ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,\left| {NP - MP} \right| < MN < NP + MP\\ \Rightarrow \left| {1 - 7} \right| < MN < 1 + 7\\ \Rightarrow 6 < MN < 8\end{array}\)
Vì độ dài cạnh \(MN\) là một số nguyên nên \(MN = 7\,\left( {cm} \right)\)
Chọn D.
Câu 7.
Phương pháp:
Dựa vào tính chất hai tam giác bằng nhau .
Cách giải:
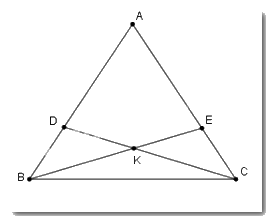
Xét tam giác ABE và tam giác ADC có
+ AD = AE (GT)
+ Góc A chung
+ AB = AC (GT)
Suy ra \(\Delta ABE = \Delta ACD\left( {c - g - c} \right)\) \( \Rightarrow \widehat {ABE} = \widehat {ACD};\widehat {ADC} = \widehat {AEB}\) (hai góc tương ứng) và BE = CD (hai cạnh tương ứng) nên A đúng.
Lại có \(\widehat {ADC} + \widehat {BDC} = {180^\circ }\); \(\widehat {AEB} + \widehat {BEC} = {180^\circ }\) (hai góc kề bù) mà \(\widehat {ADC} = \widehat {AEB}\) (cmt)
Suy ra \(\widehat {BDC} = \widehat {BEC}.\)
Lại có \(AB = AC;{\mkern 1mu} AD = AE\left( {gt} \right)\) \( \Rightarrow AB - AD = AC - AE \Rightarrow BD = EC\) nênC đúng.
Xét tam giác KBD và tam giác KCE có
+ \(\widehat {ABE} = \widehat {ACD}{\mkern 1mu} \left( {cmt} \right)\)
+ \(BD = EC{\mkern 1mu} \left( {cmt} \right)\)
+ \(\widehat {BDC} = \widehat {BEC}{\mkern 1mu} \left( {cmt} \right)\)
Nên \(\Delta KBD = \Delta KCE\left( {g - c - g} \right)\) \( \Rightarrow KB = KC;{\mkern 1mu} KD = KE\) (hai cạnh tương ứng) nên Bđúng, D sai.
Câu 8.
Phương pháp
Tính chất đồng quy của 3 đường trung trực của tam giác
Lời giải
3 đường trung trực của tam giác đồng quy tại 1 điểm, điểm này cách đều 3 đỉnh của tam giác.
Chọn C.
II. PHẦN TỰ LUẬN (8,0 điểm)
Bài 1.
Phương pháp
a) Vận dụng định nghĩa hai phân số bằng nhau: Nếu \(\dfrac{a}{b} = \dfrac{c}{d}\) thì \(ad = bc\).
b) Phương trình \(A\left( x \right).B\left( x \right) = 0\) , chia hai trường hợp để giải:
+ Trường hợp 1: \(A\left( x \right) = 0\)
+ Trường hợp 2: \(B\left( x \right) = 0\)
Cách giải:
a) \(\dfrac{{5x - 2}}{3} = \dfrac{{ - 3}}{4}\)
\(\begin{array}{l}4.\left( {5x - 2} \right) = \left( { - 3} \right).3\\20x - 8 = - 9\\20x = - 9 + 8\\20x = - 1\\x = \dfrac{{ - 1}}{{20}}\end{array}\)
Vậy \(x = \dfrac{{ - 1}}{{20}}\)
b) \(\left( {{x^2} - \dfrac{1}{4}} \right).\left( {x + \dfrac{2}{5}} \right) = 0\)
Trường hợp 1:
\(\begin{array}{l}{x^2} - \dfrac{1}{4} = 0\\{x^2} = \dfrac{1}{4} = {\left( { \pm \dfrac{1}{2}} \right)^2}\\ \Rightarrow x = \dfrac{1}{2};x = - \dfrac{1}{2}\end{array}\)
Trường hợp 2:
\(\begin{array}{l}x + \dfrac{2}{5} = 0\\x = \dfrac{{ - 2}}{5}\end{array}\)
Vậy \(x = \dfrac{1}{2};x = - \dfrac{1}{2};x = \dfrac{{ - 2}}{5}\)
Câu 2
Phương pháp:
Gọi số cây ba lớp 7A, 7B, 7C trồng được lần lượt là \(x,y,z\) (cây) (điều kiện: \(x,y,z \in {\mathbb{N}^*}\))
Áp dụng tính chất của dãy tỉ số bằng nhau để giải toán.
Cách giải:
Gọi số cây ba lớp 7A, 7B, 7C trồng được lần lượt là \(x,y,z\) (cây) (điều kiện: \(x,y,z \in {\mathbb{N}^*}\))
Vì số cây ở lớp 7A, 7B, 7C được trồng tỉ lệ với các số \(3\,;\,5\,;\,8\) nên ta có: \(\dfrac{x}{3} = \dfrac{y}{5} = \dfrac{z}{8}\)
Vì hai lần số cây của lớp 7A cộng với \(4\) lần số cây lớp 7B trồng được nhiều hơn số cây lớp 7C trồng được là \(108\) cây nên ta có: \(2x + 4y - z = 108\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: \(\dfrac{x}{3} = \dfrac{y}{5} = \dfrac{z}{8} = \dfrac{{2x}}{6} = \dfrac{{4y}}{{20}} = \dfrac{z}{8} = \dfrac{{2x + 4y - z}}{{6 + 20 - 8}} = \dfrac{{108}}{{18}} = 6\)
Khi đó, \(\dfrac{x}{3} = 6 \Rightarrow x = 18\) (tmđk)
\(\dfrac{y}{5} = 6 \Rightarrow y = 30\) (tmđk)
\(\dfrac{z}{8} = 6 \Rightarrow y = 48\) (tmđk)
Vậy số cây ba lớp trồng được là: Lớp 7A: 18 cây; lớp 7B: 30 cây, lớp 7C: 48 cây.
Bài 3.
Phương pháp:
a) Thu gọn đa thức bằng cách nhóm các hạng tử đồng dạng lại rồi thu gọn chúng. Sau đó sắp xếp theo lũy thừa giảm dần của biến.
b) Tính \(f\left( x \right) + g\left( x \right)\) ta nhóm các hạng tử đồng dạng lại rồi thu gọn chúng.
Tìm nghiệm của đa thức \(f\left( x \right) + g\left( x \right)\), ta giải phương trình \(f\left( x \right) + g\left( x \right) = 0\)
Cách giải:
a) \(f\left( x \right) = {x^5} + {x^3} - 4x - {x^5} + 3x + 7\)
\(\begin{array}{l}f\left( x \right) = \left( {{x^5} - {x^5}} \right) + {x^3} + \left( { - 4x + 3x} \right) + 7\\f\left( x \right) = {x^3} - x + 7\end{array}\)
\(\begin{array}{l}g\left( x \right) = 3{x^2} - {x^3} + 8x - 3{x^2} - 14\\g\left( x \right) = - {x^3} + \left( {3{x^2} - 3{x^2}} \right) + 8x - 14\\g\left( x \right) = - {x^3} + 8x - 14\end{array}\)
b) \(f\left( x \right) + g\left( x \right) = {x^3} - x + 7 - {x^3} + 8x - 14\)
\(\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {x^3} - x + 7 - {x^3} + 8x - 14\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {{x^3} - {x^3}} \right) + \left( { - x + 8x} \right) + \left( {7 - 14} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 7x - 7\end{array}\)
Ta có: \(f\left( x \right) + g\left( x \right) = 0\)
\(\begin{array}{l}7x - 7 = 0\\7x = 7\\\,\,\,x = 1\end{array}\)
Vậy \(x = 1\) là nghiệm của đa thức \(f\left( x \right) + g\left( x \right)\)
Bài 4.
Phương pháp:
Sử dụng tính chất tia phân giác, các phương pháp chứng minh hai tam giác vuông bằng nhau, mối quan hệ giữa cạnh và góc trong tam giác, tính chất của tam giác cân.
Cách giải:
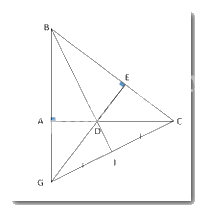
a) Chứng minh rằng ΔABD = ΔEBD.
Xét hai tam giác vuông ΔABD và ΔEBD ta có:
\(\widehat {A} =\widehat {E}=\widehat {90^0}\)
AD = DE (vì BD là tia phân giác)
BD cạnh chung
Suy ra ΔABD = ΔEBD (cạnh huyền – cạnh góc vuông) \( \Rightarrow \)AD = DE, BA = BE (cạnh tương ứng) (1)
b) So sánh AD và DC
Xét ΔDEC vuông tại E ta có: DC > DE
Lại có AD = DE (cmt)
\( \Rightarrow \)DC > AD
c) Chứng minh rằng B, D, I thẳng hàng.
Xét ΔBGC có AC \( \bot \) AB, GE \( \bot \) AC
Suy ra D là trực tâm của ΔBGC.(2)
Xét hai tam giác vuông ΔADG và ΔEDC ta có:
\(\widehat {ADG} =\widehat {EDC}\) (đối đỉnh)
\(\widehat {A} =\widehat {E}=\widehat {90^0}\)
AD = DE (cm câu b))
Suy ra ΔADG = ΔEDC (cạnh gv – góc nhọn)
\( \Rightarrow \)AG = EC (cạnh tương ứng) (3)
từ (1), (3) suy ra BA +AG = BE + EC\( \Leftrightarrow \) BG = BC
Vậy ΔBGC là tam giác cân tại B. (4)
từ (2), (4) suy ra BD là đường trung tuyến của tam giác ΔBGC. Hay B, D, I thẳng hàng. (đpcm)
Bài 5.
Phương pháp:
- Bước 1: Từ đề bài suy ra tỉ lệ
- Bước 2: Đặt các tỉ lệ bằng \(k\) từ đó suy ra \(x,{\kern 1pt} y,{\kern 1pt} z\) theo \(k\)
- Bước 3: Thay vào đề bài và tính toán
- Bước 4: Kết luận
Cách giải:
Vì \(x;\,{\kern 1pt} y;{\kern 1pt} \,z\) tỉ lệ thuận với \(3;{\kern 1pt} \,\,4;\,\,{\kern 1pt} 5\) \( \Rightarrow \dfrac{x}{3} = \dfrac{y}{4} = \dfrac{z}{5}\). Đặt \(\dfrac{x}{3} = \dfrac{y}{4} = \dfrac{z}{5} = k \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = 3k}\\{y = 4k}\\{z = 5k}\end{array}} \right.\). Khi đó,\(A = 2024\left( {3k - 4k} \right)\left( {4k - 5k} \right) - 506.{\left( {\dfrac{{3k + 4k + 5k}}{6}} \right)^2}\)
\(A = 2024\left( { - k} \right)\left( { - k} \right) - 506.{\left( {2k} \right)^2}\)
\(A = 2024.{k^2} - 506.4.{k^2}\)
\(A = 2024{k^2} - 2024{k^2}\)
\(A = 0\)
Vậy \(A = 0.\)
I. Trắc nghiệm
1. B | 2. D | 3. A | 4. C |
5. A | 6. D | 7. D | 8. C |
Câu 1.
Phương pháp:
Vận dụng định nghĩa về đại lượng tỉ lệ nghịch.
Cách giải:
Ta có: \(x = \dfrac{5}{y}\) là hai đại lượng tỉ lệ nghịch với nhau.
Chọn B.
Câu 2.
Phương pháp:
Biến cố chắc chắn: Là biến cố biết trước được luôn xảy ra
Cách giải:
Đáp án ABiến cố không thể
Đáp án BBiến cố ngẫu nhiên
Đáp án CBiến cố ngẫu nhiên
Đáp án DMặt Trời luôn mọc ở phía Đông nên sự kiện “Ngày mai, Mặt Trời mọc ở phía Đông." Luôn xảy ra nên là biến
cố chắc chắn.
Chọn D.
Câu 3.
Phương pháp:
Áp dụng công thức tính tính chu vi hình chữ nhật và công thức tính thể tích hình hộp chữ nhật.
Cách giải:
Gọi độ dài các cạnh đáy của hình hộp chữ nhật là \(a\) và \(b,\) chiều cao là \(c\,\,\,\left( {a,b,c \in {\mathbb{N}^*}} \right).\)
Vì chu vi đáy của hình hộp chữ nhật là \(18\,cm\) nên ta có: \(2\left( {a + b} \right) = 18 \Rightarrow a + b = \dfrac{{18}}{2} = 9\,\,\,\,\left( 1 \right)\)
Thể tích khối lập phương cạnh \(1cm\) là: \({V_1} = {1^3} = 1\left( {c{m^3}} \right)\)
Thể tích của hình hộp chữ nhật là: \(V = 42.1 = 42\left( {c{m^3}} \right)\) \( \Rightarrow abc = 42\,\,\,\left( 2 \right)\)
Từ \(\left( 1 \right),\left( 2 \right) \Rightarrow \)\(a,\,b\) là ước của \(42\) và nhỏ hơn \(9.\)
+ Nếu các cạnh đáy là \(5\) và \(4\) thì \(c = \dfrac{{42}}{{a.b}} = \dfrac{{42}}{{5.4}} = \dfrac{{21}}{{10}}\,\) không là số tự nhiên
+ Nếu các cạnh đáy là \(6\) và \(3\) thì \(c = \dfrac{{42}}{{a.b}} = \dfrac{{42}}{{6.3}} = \dfrac{7}{3}\,\) không là số tự nhiên
+ Nếu các cạnh đáy là \(7\) và \(2\) thì \(c = \dfrac{{42}}{{a.b}} = \dfrac{{42}}{{7.2}} = 3\,\left( {TM} \right)\,\)
Vậy các cạnh của hình chữ nhật là \(7cm;\,2cm;\,3cm\) nên tổng ba kích thước của hình hộp chữ nhật là \(12cm.\)
Chọn A.
Câu 4.
Phương pháp:
Đơn thức là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và các biến.
Cách giải:
Biểu thức: \(2xy - {x^2}\) không là một đơn thức.
Chọn C.
Câu 5.
Phương pháp:
Thu gọn đa thức bằng cách nhóm các hạng tử đồng dạng lại rồi thu gọn chúng. Sau đó sắp xếp theo lũy thừa giảm dần của biến.
Cách giải:
Sắp xếp theo lũy thừa giảm dần của biến: \(P\left( x \right) = {x^4} + 2{x^3} - 7{x^2} - 4\)
Chọn A.
Câu 6.
Phương pháp:
Sử dụng hệ quả của bất đẳng thức trong tam giác:
+ Tồn tại một tam giác có độ dài ba cạnh là \(a,b,c\) nếu \(\left| {b - c} \right| < a < b + c\).
+ Trong trường hợp xác định được \(a\) là số lớn nhất trong ba số \(a,b,c\) thì điều kiện tồn tại tam giác là \(a < b + c\).
Cách giải:
Xét tam giác \(MNP\), ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,\left| {NP - MP} \right| < MN < NP + MP\\ \Rightarrow \left| {1 - 7} \right| < MN < 1 + 7\\ \Rightarrow 6 < MN < 8\end{array}\)
Vì độ dài cạnh \(MN\) là một số nguyên nên \(MN = 7\,\left( {cm} \right)\)
Chọn D.
Câu 7.
Phương pháp:
Dựa vào tính chất hai tam giác bằng nhau .
Cách giải:
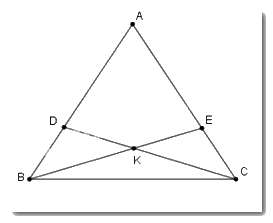
Xét tam giác ABE và tam giác ADC có
+ AD = AE (GT)
+ Góc A chung
+ AB = AC (GT)
Suy ra \(\Delta ABE = \Delta ACD\left( {c - g - c} \right)\) \( \Rightarrow \widehat {ABE} = \widehat {ACD};\widehat {ADC} = \widehat {AEB}\) (hai góc tương ứng) và BE = CD (hai cạnh tương ứng) nên A đúng.
Lại có \(\widehat {ADC} + \widehat {BDC} = {180^\circ }\); \(\widehat {AEB} + \widehat {BEC} = {180^\circ }\) (hai góc kề bù) mà \(\widehat {ADC} = \widehat {AEB}\) (cmt)
Suy ra \(\widehat {BDC} = \widehat {BEC}.\)
Lại có \(AB = AC;{\mkern 1mu} AD = AE\left( {gt} \right)\) \( \Rightarrow AB - AD = AC - AE \Rightarrow BD = EC\) nênC đúng.
Xét tam giác KBD và tam giác KCE có
+ \(\widehat {ABE} = \widehat {ACD}{\mkern 1mu} \left( {cmt} \right)\)
+ \(BD = EC{\mkern 1mu} \left( {cmt} \right)\)
+ \(\widehat {BDC} = \widehat {BEC}{\mkern 1mu} \left( {cmt} \right)\)
Nên \(\Delta KBD = \Delta KCE\left( {g - c - g} \right)\) \( \Rightarrow KB = KC;{\mkern 1mu} KD = KE\) (hai cạnh tương ứng) nên Bđúng, D sai.
Câu 8.
Phương pháp
Tính chất đồng quy của 3 đường trung trực của tam giác
Lời giải
3 đường trung trực của tam giác đồng quy tại 1 điểm, điểm này cách đều 3 đỉnh của tam giác.
Chọn C.
II. PHẦN TỰ LUẬN (8,0 điểm)
Bài 1.
Phương pháp
a) Vận dụng định nghĩa hai phân số bằng nhau: Nếu \(\dfrac{a}{b} = \dfrac{c}{d}\) thì \(ad = bc\).
b) Phương trình \(A\left( x \right).B\left( x \right) = 0\) , chia hai trường hợp để giải:
+ Trường hợp 1: \(A\left( x \right) = 0\)
+ Trường hợp 2: \(B\left( x \right) = 0\)
Cách giải:
a) \(\dfrac{{5x - 2}}{3} = \dfrac{{ - 3}}{4}\)
\(\begin{array}{l}4.\left( {5x - 2} \right) = \left( { - 3} \right).3\\20x - 8 = - 9\\20x = - 9 + 8\\20x = - 1\\x = \dfrac{{ - 1}}{{20}}\end{array}\)
Vậy \(x = \dfrac{{ - 1}}{{20}}\)
b) \(\left( {{x^2} - \dfrac{1}{4}} \right).\left( {x + \dfrac{2}{5}} \right) = 0\)
Trường hợp 1:
\(\begin{array}{l}{x^2} - \dfrac{1}{4} = 0\\{x^2} = \dfrac{1}{4} = {\left( { \pm \dfrac{1}{2}} \right)^2}\\ \Rightarrow x = \dfrac{1}{2};x = - \dfrac{1}{2}\end{array}\)
Trường hợp 2:
\(\begin{array}{l}x + \dfrac{2}{5} = 0\\x = \dfrac{{ - 2}}{5}\end{array}\)
Vậy \(x = \dfrac{1}{2};x = - \dfrac{1}{2};x = \dfrac{{ - 2}}{5}\)
Câu 2
Phương pháp:
Gọi số cây ba lớp 7A, 7B, 7C trồng được lần lượt là \(x,y,z\) (cây) (điều kiện: \(x,y,z \in {\mathbb{N}^*}\))
Áp dụng tính chất của dãy tỉ số bằng nhau để giải toán.
Cách giải:
Gọi số cây ba lớp 7A, 7B, 7C trồng được lần lượt là \(x,y,z\) (cây) (điều kiện: \(x,y,z \in {\mathbb{N}^*}\))
Vì số cây ở lớp 7A, 7B, 7C được trồng tỉ lệ với các số \(3\,;\,5\,;\,8\) nên ta có: \(\dfrac{x}{3} = \dfrac{y}{5} = \dfrac{z}{8}\)
Vì hai lần số cây của lớp 7A cộng với \(4\) lần số cây lớp 7B trồng được nhiều hơn số cây lớp 7C trồng được là \(108\) cây nên ta có: \(2x + 4y - z = 108\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: \(\dfrac{x}{3} = \dfrac{y}{5} = \dfrac{z}{8} = \dfrac{{2x}}{6} = \dfrac{{4y}}{{20}} = \dfrac{z}{8} = \dfrac{{2x + 4y - z}}{{6 + 20 - 8}} = \dfrac{{108}}{{18}} = 6\)
Khi đó, \(\dfrac{x}{3} = 6 \Rightarrow x = 18\) (tmđk)
\(\dfrac{y}{5} = 6 \Rightarrow y = 30\) (tmđk)
\(\dfrac{z}{8} = 6 \Rightarrow y = 48\) (tmđk)
Vậy số cây ba lớp trồng được là: Lớp 7A: 18 cây; lớp 7B: 30 cây, lớp 7C: 48 cây.
Bài 3.
Phương pháp:
a) Thu gọn đa thức bằng cách nhóm các hạng tử đồng dạng lại rồi thu gọn chúng. Sau đó sắp xếp theo lũy thừa giảm dần của biến.
b) Tính \(f\left( x \right) + g\left( x \right)\) ta nhóm các hạng tử đồng dạng lại rồi thu gọn chúng.
Tìm nghiệm của đa thức \(f\left( x \right) + g\left( x \right)\), ta giải phương trình \(f\left( x \right) + g\left( x \right) = 0\)
Cách giải:
a) \(f\left( x \right) = {x^5} + {x^3} - 4x - {x^5} + 3x + 7\)
\(\begin{array}{l}f\left( x \right) = \left( {{x^5} - {x^5}} \right) + {x^3} + \left( { - 4x + 3x} \right) + 7\\f\left( x \right) = {x^3} - x + 7\end{array}\)
\(\begin{array}{l}g\left( x \right) = 3{x^2} - {x^3} + 8x - 3{x^2} - 14\\g\left( x \right) = - {x^3} + \left( {3{x^2} - 3{x^2}} \right) + 8x - 14\\g\left( x \right) = - {x^3} + 8x - 14\end{array}\)
b) \(f\left( x \right) + g\left( x \right) = {x^3} - x + 7 - {x^3} + 8x - 14\)
\(\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {x^3} - x + 7 - {x^3} + 8x - 14\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {{x^3} - {x^3}} \right) + \left( { - x + 8x} \right) + \left( {7 - 14} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 7x - 7\end{array}\)
Ta có: \(f\left( x \right) + g\left( x \right) = 0\)
\(\begin{array}{l}7x - 7 = 0\\7x = 7\\\,\,\,x = 1\end{array}\)
Vậy \(x = 1\) là nghiệm của đa thức \(f\left( x \right) + g\left( x \right)\)
Bài 4.
Phương pháp:
Sử dụng tính chất tia phân giác, các phương pháp chứng minh hai tam giác vuông bằng nhau, mối quan hệ giữa cạnh và góc trong tam giác, tính chất của tam giác cân.
Cách giải:
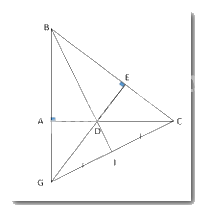
a) Chứng minh rằng ΔABD = ΔEBD.
Xét hai tam giác vuông ΔABD và ΔEBD ta có:
\(\widehat {A} =\widehat {E}=\widehat {90^0}\)
AD = DE (vì BD là tia phân giác)
BD cạnh chung
Suy ra ΔABD = ΔEBD (cạnh huyền – cạnh góc vuông) \( \Rightarrow \)AD = DE, BA = BE (cạnh tương ứng) (1)
b) So sánh AD và DC
Xét ΔDEC vuông tại E ta có: DC > DE
Lại có AD = DE (cmt)
\( \Rightarrow \)DC > AD
c) Chứng minh rằng B, D, I thẳng hàng.
Xét ΔBGC có AC \( \bot \) AB, GE \( \bot \) AC
Suy ra D là trực tâm của ΔBGC.(2)
Xét hai tam giác vuông ΔADG và ΔEDC ta có:
\(\widehat {ADG} =\widehat {EDC}\) (đối đỉnh)
\(\widehat {A} =\widehat {E}=\widehat {90^0}\)
AD = DE (cm câu b))
Suy ra ΔADG = ΔEDC (cạnh gv – góc nhọn)
\( \Rightarrow \)AG = EC (cạnh tương ứng) (3)
từ (1), (3) suy ra BA +AG = BE + EC\( \Leftrightarrow \) BG = BC
Vậy ΔBGC là tam giác cân tại B. (4)
từ (2), (4) suy ra BD là đường trung tuyến của tam giác ΔBGC. Hay B, D, I thẳng hàng. (đpcm)
Bài 5.
Phương pháp:
- Bước 1: Từ đề bài suy ra tỉ lệ
- Bước 2: Đặt các tỉ lệ bằng \(k\) từ đó suy ra \(x,{\kern 1pt} y,{\kern 1pt} z\) theo \(k\)
- Bước 3: Thay vào đề bài và tính toán
- Bước 4: Kết luận
Cách giải:
Vì \(x;\,{\kern 1pt} y;{\kern 1pt} \,z\) tỉ lệ thuận với \(3;{\kern 1pt} \,\,4;\,\,{\kern 1pt} 5\) \( \Rightarrow \dfrac{x}{3} = \dfrac{y}{4} = \dfrac{z}{5}\). Đặt \(\dfrac{x}{3} = \dfrac{y}{4} = \dfrac{z}{5} = k \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = 3k}\\{y = 4k}\\{z = 5k}\end{array}} \right.\). Khi đó,\(A = 2024\left( {3k - 4k} \right)\left( {4k - 5k} \right) - 506.{\left( {\dfrac{{3k + 4k + 5k}}{6}} \right)^2}\)
\(A = 2024\left( { - k} \right)\left( { - k} \right) - 506.{\left( {2k} \right)^2}\)
\(A = 2024.{k^2} - 506.4.{k^2}\)
\(A = 2024{k^2} - 2024{k^2}\)
\(A = 0\)
Vậy \(A = 0.\)
Kỳ thi học kì 2 Toán 7 là một bước quan trọng để đánh giá năng lực học tập của học sinh sau một học kỳ rèn luyện. Đề thi học kì 2 Toán 7 - Đề số 4 - Kết nối tri thức là một trong những đề thi được nhiều trường học lựa chọn để đánh giá học sinh. Bài viết này sẽ cung cấp thông tin chi tiết về cấu trúc đề thi, các dạng bài tập thường gặp và hướng dẫn giải chi tiết để giúp các em học sinh ôn tập hiệu quả.
Đề thi học kì 2 Toán 7 - Đề số 4 - Kết nối tri thức thường bao gồm các phần sau:
Các chủ đề thường xuất hiện trong đề thi bao gồm:
Dưới đây là một số dạng bài tập thường gặp trong Đề thi học kì 2 Toán 7 - Đề số 4 - Kết nối tri thức:
Các bài tập thuộc dạng này yêu cầu học sinh thực hiện các phép toán cộng, trừ, nhân, chia với số hữu tỉ. Để giải các bài tập này, học sinh cần nắm vững các quy tắc về phép toán với số hữu tỉ.
Các bài tập thuộc dạng này yêu cầu học sinh giải các phương trình bậc nhất một ẩn. Để giải các bài tập này, học sinh cần nắm vững các bước giải phương trình bậc nhất một ẩn.
Các bài tập thuộc dạng này yêu cầu học sinh chứng minh hai tam giác bằng nhau. Để giải các bài tập này, học sinh cần nắm vững các trường hợp bằng nhau của tam giác.
Các bài tập thuộc dạng này yêu cầu học sinh vận dụng các tính chất của đường thẳng song song, đường thẳng vuông góc để giải quyết các bài toán hình học.
Ví dụ 1: Tính giá trị của biểu thức A = (1/2 + 1/3) * 6/5
Giải:
Ví dụ 2: Giải phương trình 2x + 3 = 7
Giải:
Đề thi học kì 2 Toán 7 - Đề số 4 - Kết nối tri thức là một cơ hội để các em học sinh thể hiện kiến thức và kỹ năng đã học. Hy vọng với những thông tin và hướng dẫn trên, các em sẽ tự tin hơn khi bước vào kỳ thi. Chúc các em đạt kết quả tốt nhất!