Chào mừng các em học sinh lớp 7 đến với đề thi học kì 1 môn Toán - Đề số 13, chương trình Kết nối tri thức. Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong học kì 1.
Giaitoan.edu.vn cung cấp đề thi chính thức, đáp án chi tiết và lời giải bài tập để các em có thể tự học và nâng cao kỹ năng giải toán.
Căn bậc hai số học của 36 là:
Khẳng định nào sau đây đúng?
Cho \(\left| x \right|\) = 9 thì giá trị của x là:
Cho đoạn thẳng \(AB\) có độ dài \(6\)cm, đường trung trực của đoạn thẳng \(AB\) cắt \(AB\) tại \(I\), kết luận nào sau đây là đúng?
Cho hình vẽ sau có \(\widehat {CBA} = 50^\circ \). Số đo \(\widehat D\) bằng
Hãy điền vào chỗ “….” để được khẳng định đúng: Qua một điểm M nằm ngoài đường thẳng a …............. đường thẳng song song với đường thẳng a.
Cho góc nhọn \(\widehat {xOy}\)có tia phân giác \(Ot\), trên tia \(Ot\) lấy điểm \(H\), từ \(H\) kẻ đường vuông góc với tia \(Ox\) tại \(A\), đường vuông góc với tia \(Oy\) tại \(B\). Nhận xét nào sau đây sai
Biểu đồ hình quạt tròn ở hình bên biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) chọn môn thể thao ưa thích nhất trong bốn môn: Bóng đá, Cầu lông, Bóng bàn, Bóng chuyền của học sinh khối 7 ở trường A. Mỗi học sinh chỉ được chọn một môn thể thao khi được hỏi ý kiến. Hỏi số học sinh chọn môn Bóng đá và Cầu lông.
Trong các số sau, số nào biểu diễn số thập phân vô hạn tuần hoàn?
Quan sát hình vẽ bên dưới, tia phân giác của góc xOy là:
Cho hình vẽ bên, biết a // b. Số đo là bao nhiêu?
Hình vẽ nào sau đây không có hai đường thẳng song song?
a) Tính: \(\frac{7}{{10}} \cdot \frac{{15}}{{19}} + \frac{7}{{10}} \cdot \frac{4}{{19}}\).
b) Tìm x, biết: \(0,8 - \left( {{\rm{x + }}\frac{3}{5}} \right) = \frac{1}{2}\).
Viết giả thiết, kết luận của định lí: “Nếu hai đường thẳng a và b phân biệt cùng vuông góc với một đường thẳng c thì a và b song song với nhau”.
Tính các căn bậc hai số học của các số sau (kết quả làm tròn đến hàng phần trăm)
a) \(\sqrt {31} \)
b) \(\sqrt {123} \)
c) \( - 200\sqrt 5 \)
Quan sát hình vẽ sau.
Giải thích vì sao BC song song với EF?
Cho \(\Delta ABC\)vuông ở \(C\), có \(\widehat A = {60^o}\), tia phân giác của góc \(BAC\) cắt \(BC\) ở \(E\), kẻ \(EK\) vuông góc với \(AB\) (\(K\) thuộc \(AB\)), kẻ \(BD\) vuông góc với \(AE\) (\(D\) thuộc \(AE\))
Chứng minh:
a) \(AK{\rm{ }} = {\rm{ }}KB\);
b) \(AD{\rm{ }} = {\rm{ }}BC\)
Số học sinh yêu thích các môn thể thao: đá bóng, đá cầu, cầu lông, bơi và môn thể thao khác của một trường THCS được biểu diễn qua biểu đồ hình quạt tròn dưới đây. Tính số phần trăm học sinh yêu thích môn thể thao khác?
Tính đến ngày 01/04/2019 Việt Nam là quốc gia đông dân thứ ba trong khu vực Đông Nam Á. Tổng số dân của Việt Nam là 96 208 984 người, trong đó dân số nam là 47 881 061 người và dân số nữ là 48 327 923 người. Hãy làm tròn các số liệu về dân số nam và dân số nữ nêu trên đến hàng nghìn.
Kết quả tìm hiểu về mức độ yêu thích đối với việc đọc sách trong thư viện của các bạn nam lớp 7C tại một trường Trung học cơ sở được cho bởi bảng thống kê sau:

a) Hãy phân loại các dữ liệu trong bảng thống kê trên dựa vào tiêu chí định tính và định lượng.
b) Biết lớp 7C có 50 học sinh. Hỏi dữ liệu trên có đại diện được cho mức độ yêu thích đối với việc đọc sách trong thư viện của các bạn học sinh lớp 7C hay không? Vì sao?
Một người luyện tập chạy bộ từ nhà đến một công viên ở cách đó 874,8 m đường bộ với tốc độ là 97,2 (m/phút). Khi đến công viên, người này đã ở đây trong 10 phút để chơi cầu lông cùng nhóm bạn. Sau đó người này đã chạy bộ theo đường cũ từ công viên về nhà và dừng lại tại một quán cà phê cách nhà 360 m đường bộ. Biết rằng tổng thời gian từ lúc bắt đầu chạy bộ từ nhà cho đến khi dừng ở quán cà phê là 34,6 phút và quán này nằm trên đoạn đường từ nhà đến công viên. Hỏi khi chạy bộ từ công viên đến quán cà phê, tốc độ của người đó là bao nhiêu? (đơn vị đo là m/phút)
Căn bậc hai số học của 36 là:
Đáp án : B
Sử dụng kiến thức về căn bậc hai số học: Căn bậc hai số học của số a không âm là số x không âm sao cho \({x^2} = a\).
Căn bậc hai số học của 36 là \(\sqrt {36} = 6\).
Khẳng định nào sau đây đúng?
Đáp án : C
\(\mathbb{R}\) là tập hợp các số thực.
\(I\) là tập hợp các số vô tỉ.
\( - 1,\left( 3 \right)\) là số thực nên A sai.
\(3,5 = \frac{{35}}{{10}} = \frac{7}{2}\) là số hữu tỉ nên không phải là số vô tỉ, do đó \(3,5 \notin \,{\rm{I}}\) nên B sai.
\(\pi = 3,14...\) là số thực, \(\pi \, \in \,\,\mathbb{R}\) nên C đúng.
\(\sqrt {11} \) là số vô tỉ nên D sai.
Cho \(\left| x \right|\) = 9 thì giá trị của x là:
Đáp án : A
Dựa vào kiến thức về dấu giá trị tuyệt đối.
Ta có: \(\left| x \right| = 9\) thì x = 9 hoặc x = –9.
Cho đoạn thẳng \(AB\) có độ dài \(6\)cm, đường trung trực của đoạn thẳng \(AB\) cắt \(AB\) tại \(I\), kết luận nào sau đây là đúng?
Đáp án : C
Dựa vào tính chất của đường trung trực của đoạn thẳng.
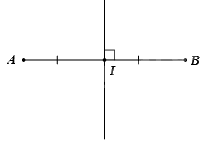
Đường trung trực của đoạn thẳng \(AB\)cắt \(AB\) tại \(I\) nên \(I\) là trung điểm của \(AB\)
Suy ra: \(IA = IB = \frac{{AB}}{2} = \frac{6}{2} = 3{\rm{ cm}}\)
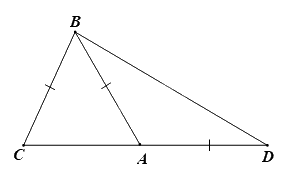
Cho hình vẽ sau có \(\widehat {CBA} = 50^\circ \). Số đo \(\widehat D\) bằng
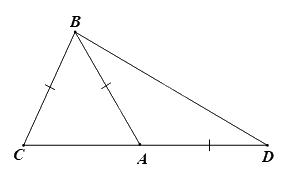
Đáp án : C
- Dựa vào tính chất của tam giác cân
- Tính chất tổng 3 góc của tam giác bằng 1800.
- Tính chất hai góc kề bù.
Xét tam giác ABC có AB = BC nên tam giác ABC cân tại B.
\( \Rightarrow \widehat {BAC} = \widehat {BCA}\)
Mà \(\widehat {CBA} = 50^\circ \) nên \(\widehat {BAC} = \widehat {BCA} = \frac{{{{180}^0} - {{50}^0}}}{2} = {65^0}\).
\(\widehat {BAC} + \widehat {BAD} = {180^0} \Rightarrow \widehat {BAD} = {180^0} - {65^0} = {115^0}\).
Xét tam giác ABD có AB = AD nên tam giác ABD cân tại A \( \Rightarrow \widehat {ABD} = \widehat {ADB} = \frac{{{{180}^0} - {{115}^0}}}{2} = 32,{5^0}\).
Hãy điền vào chỗ “….” để được khẳng định đúng: Qua một điểm M nằm ngoài đường thẳng a …............. đường thẳng song song với đường thẳng a.
Đáp án : A
Dựa vào kiến thức về các đường thẳng song song.
Qua một điểm M nằm ngoài đường thẳng a chỉ có một đường thẳng song song với đường thẳng a.
Cho góc nhọn \(\widehat {xOy}\)có tia phân giác \(Ot\), trên tia \(Ot\) lấy điểm \(H\), từ \(H\) kẻ đường vuông góc với tia \(Ox\) tại \(A\), đường vuông góc với tia \(Oy\) tại \(B\). Nhận xét nào sau đây sai
Đáp án : B
Dựa vào tính chất đường phân giác và các trường hợp bằng nhau của tam giác vuông.
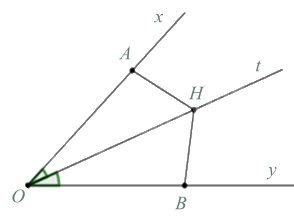
Vì \(Ot\) là tia phân giác của góc nhọn \(\widehat {xOy}\) nên \(\widehat {AOH} = \widehat {BOH}\), do vậy A đúng
Vì \(\Delta HAO = \Delta HBO\)(cạnh huyền – góc nhọn) nên D đúng. Đồng thời suy ra \(HA = HB\) nên C cũng đúng.
Chỉ có B sai.
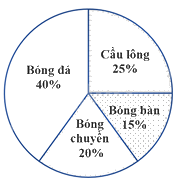
Biểu đồ hình quạt tròn ở hình bên biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) chọn môn thể thao ưa thích nhất trong bốn môn: Bóng đá, Cầu lông, Bóng bàn, Bóng chuyền của học sinh khối 7 ở trường A. Mỗi học sinh chỉ được chọn một môn thể thao khi được hỏi ý kiến. Hỏi số học sinh chọn môn Bóng đá và Cầu lông.
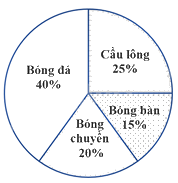
Đáp án : B
Quan sát biểu đồ để xác định số phần trăm học sinh chọn môn Bóng đá và Cầu lông.
Số học sinh chọn môn Bóng đá chiếm 40%, số học sinh chọn môn Cầu lông chiếm 25% nên tổng số học sinh chọn môn Bóng đá và Cầu lông chiếm: 40% + 25% = 65% tổng số học sinh.
Trong các số sau, số nào biểu diễn số thập phân vô hạn tuần hoàn?
Đáp án : C
Các phân số tối giản với mẫu số dương mà mẫu có ước nguyên tố khác 2 và 5 đều viết được dưới dạng số thập phân vô hạn tuần hoàn.
\(\frac{1}{{10}}\) và \(\frac{2}{5}\) có mẫu chỉ có ước nguyên tố là 2 và 5 nên không biểu diễn số thập phân vô hạn tuần hoàn.
\(\frac{7}{6}\) mẫu số có ước là 2 và 3 nên biểu diễn số thập phân vô hạn tuần hoàn.
\(\sqrt {13} \) không viết được dưới dạng phân số nên không phải số thập phân vô hạn tuần hoàn.
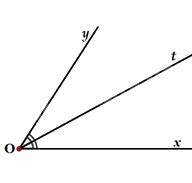
Quan sát hình vẽ bên dưới, tia phân giác của góc xOy là:
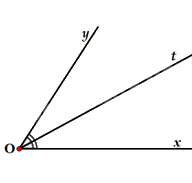
Đáp án : C
Dựa vào tính chất tia phân giác của một góc: \(Ot\) là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOt} = \widehat {tOy} = \frac{1}{2}\widehat {xOy}\).
Vì \(\widehat {xOt} = \widehat {tOy}\) và Ot nằm trong góc xOy nên Ot là tia phân giác của góc xOy.
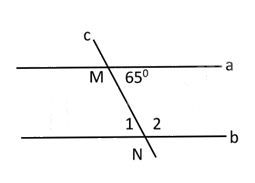
Cho hình vẽ bên, biết a // b. Số đo là bao nhiêu?
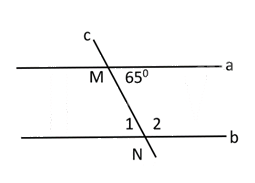
Đáp án : B
Dựa vào tính chất của hai đường thẳng song song: Hai đường thẳng song song với nhau thì hai góc so le trong bằng nhau.
Vì a // b nên \(\widehat {{N_1}} = \widehat {NMa} = {65^0}\) (2 góc so le trong).
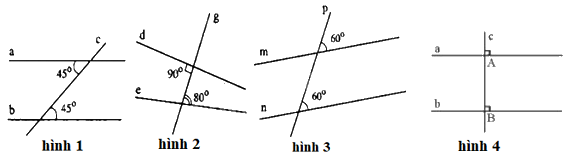
Hình vẽ nào sau đây không có hai đường thẳng song song?
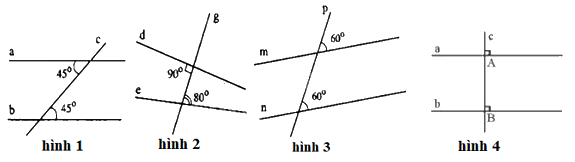
Đáp án : B
Dựa vào dấu hiệu nhận biết hai đường thẳng song song.
Hình 1 có hai góc so le trong bằng nhau (= 450) nên hình 1 có hai đường thẳng song song.
Hình 2 hai góc so le trong không bằng nhau nên hình 2 không có hai đường thẳng song song.
Hình 3 có hai góc đồng vị bằng nhau (= 600) nên hình 3 có hai đường thẳng song song.
Hình 4 có hai góc đồng vị bằng nhau (= 900) nên hình 4 có hai đường thẳng song song.
a) Tính: \(\frac{7}{{10}} \cdot \frac{{15}}{{19}} + \frac{7}{{10}} \cdot \frac{4}{{19}}\).
b) Tìm x, biết: \(0,8 - \left( {{\rm{x + }}\frac{3}{5}} \right) = \frac{1}{2}\).
a) Nhóm nhân tử chung để tính.
b) Sử dụng quy tắc chuyển vế để tìm x.
a) \(\frac{7}{{10}} \cdot \frac{{15}}{{19}} + \frac{7}{{10}} \cdot \frac{4}{{19}}\)
\(\begin{array}{l} = \frac{7}{{10}}\left( {\frac{{15}}{{19}} + \frac{4}{{19}}} \right)\\ = \frac{7}{{10}}.1\\ = \frac{7}{{10}}\end{array}\)
b) \(0,8 - \left( {{\rm{x + }}\frac{3}{5}} \right) = \frac{1}{2}\)
\(\begin{array}{l}\frac{4}{5} - \left( {{\rm{x + }}\frac{3}{5}} \right) = \frac{1}{2}\\x + \frac{3}{5} = \frac{4}{5} - \frac{1}{2}\\x + \frac{3}{5} = \frac{3}{{10}}\\x = \frac{3}{{10}} - \frac{3}{5}\\x = \frac{{ - 3}}{{10}}\end{array}\)
Vậy \(x = \frac{{ - 3}}{{10}}\).
Viết giả thiết, kết luận của định lí: “Nếu hai đường thẳng a và b phân biệt cùng vuông góc với một đường thẳng c thì a và b song song với nhau”.
Khi giả thiết được phát biểu dưới dạng: “Nếu … thì”, phần giữa từ “nếu” và từ “thì” là giả thiết của định lí, phần sau từ “thì” là kết luận của định lí.
- Giả thiết: hai đường thẳng a và b phân biệt cùng vuông góc với một đường thẳng c
- Kết luận: a và b song song với nhau.
Tính các căn bậc hai số học của các số sau (kết quả làm tròn đến hàng phần trăm)
a) \(\sqrt {31} \)
b) \(\sqrt {123} \)
c) \( - 200\sqrt 5 \)
Sử dụng kiến thức về căn bậc hai số học: Căn bậc hai số học của số a không âm là số x không âm sao cho \({x^2} = a\).
a) \(\sqrt {31} = 5,567764363... \approx 5,57\).
b) \(\sqrt {123} = 11,09053651... \approx 11,09\).
c) \( - 200\sqrt 5 = - 447,2135955... \approx - 447,21\).
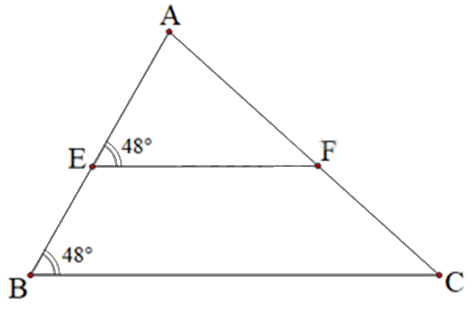
Quan sát hình vẽ sau.
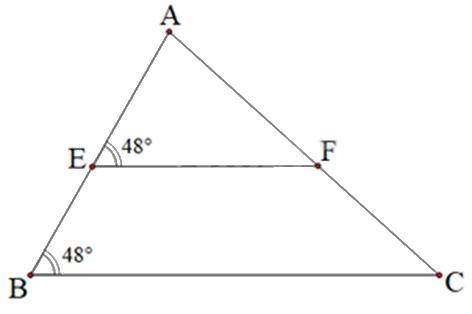
Giải thích vì sao BC song song với EF?
Dựa vào dấu hiệu nhận biết hai đường thẳng song song.
Ta có : \(\widehat {AEF} = \widehat {ABC} = {48^0}\) Mà hai góc này ở vị trí đồng vị \( \Rightarrow \) BC // EF.
Cho \(\Delta ABC\)vuông ở \(C\), có \(\widehat A = {60^o}\), tia phân giác của góc \(BAC\) cắt \(BC\) ở \(E\), kẻ \(EK\) vuông góc với \(AB\) (\(K\) thuộc \(AB\)), kẻ \(BD\) vuông góc với \(AE\) (\(D\) thuộc \(AE\))
Chứng minh:
a) \(AK{\rm{ }} = {\rm{ }}KB\);
b) \(AD{\rm{ }} = {\rm{ }}BC\)
Sử dụng tính chất tam giác cân và dấu hiệu nhận biết hai tam giác bằng nhau suy ra các cạnh tương ứng bằng nhau.
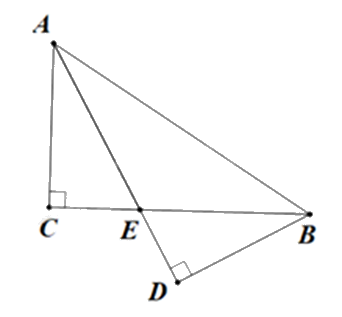
a) Ta có:
\(\widehat {EAB} = \frac{1}{2}\widehat {.BAC} = \frac{1}{2}{.60^{\rm{o}}} = {30^{\rm{o}}}\)(\(AE\) là phân giác của góc \(BAC\))
\(\widehat {ABC} = {90^{\rm{o}}} - \widehat {BAC} = {90^{\rm{o}}} - {60^{\rm{o}}} = {30^o}\)(Vì \(\Delta ABC\) vuông tại \(C\))
Suy ra \(\widehat {EAB} = \widehat {ABC}\)
\( \Rightarrow \Delta EAB\) cân tại \(E\)
Vậy \(EA{\rm{ }} = {\rm{ }}EB\)
* Xét \(\;\Delta EAK\)và \(\Delta EBK\)có:
\(\widehat {EKA} = \widehat {EKB} = {90^o}\)
\(EA{\rm{ }} = {\rm{ }}EB\) (chứng minh trên)
\(\widehat {EAB} = \widehat {ABC} = {30^o}\)
Suy ra \(\Delta EAK = \Delta EBK\)(cạnh huyền – góc nhọn)
Vậy \(KA = KB\;\)(2 cạnh tương ứng)
b) Xét \(\Delta CAB\) và \(\Delta DBA\)có:
\(\widehat {ACB} = \widehat {BDA} = {90^o}\)
\(AB\) chung
\(\widehat {ABC} = \widehat {BAD} = {30^o}\)
Suy ra \(\Delta CAB = \Delta DBA\)(cạnh huyền – góc nhọn)
Vậy\(BC = AD\) (2 cạnh tương ứng)
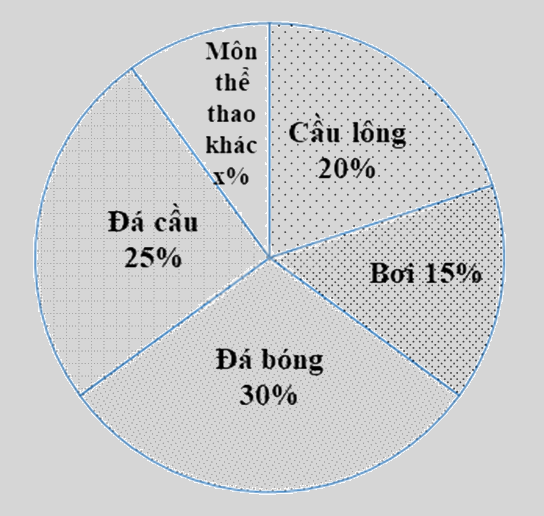
Số học sinh yêu thích các môn thể thao: đá bóng, đá cầu, cầu lông, bơi và môn thể thao khác của một trường THCS được biểu diễn qua biểu đồ hình quạt tròn dưới đây. Tính số phần trăm học sinh yêu thích môn thể thao khác?
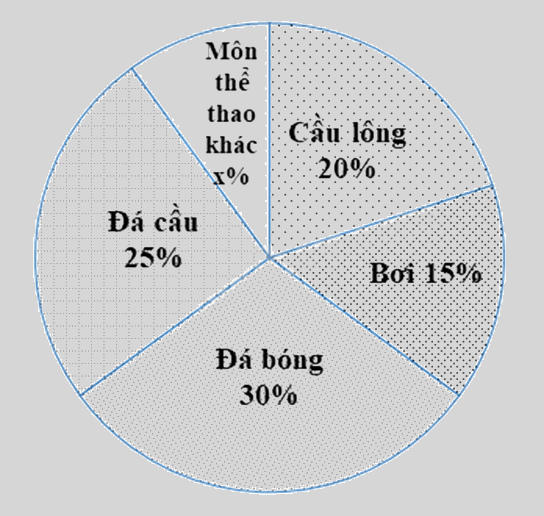
Vì tổng số phần trăm học sinh là 100% nên số phần trăm học sinh yêu thích môn thể thao khác bằng 100% - số phần trăm học sinh thích các môn thể thao còn lại (đá bóng, đá cầu, cầu lông, bơi).
Số phần trăm học sinh yêu thích các môn thể thao khác là:
100% – (20% + 15% + 30% + 25%) = 10% (số học sinh trường)
Tính đến ngày 01/04/2019 Việt Nam là quốc gia đông dân thứ ba trong khu vực Đông Nam Á. Tổng số dân của Việt Nam là 96 208 984 người, trong đó dân số nam là 47 881 061 người và dân số nữ là 48 327 923 người. Hãy làm tròn các số liệu về dân số nam và dân số nữ nêu trên đến hàng nghìn.
Sử dụng cách làm tròn số.
- Dân số nam: 47 881 061 $\approx $ 47 881 000 người.
- Dân số nữ: 48 327 923 $\approx $ 48 328 000 người.
Kết quả tìm hiểu về mức độ yêu thích đối với việc đọc sách trong thư viện của các bạn nam lớp 7C tại một trường Trung học cơ sở được cho bởi bảng thống kê sau:

a) Hãy phân loại các dữ liệu trong bảng thống kê trên dựa vào tiêu chí định tính và định lượng.
b) Biết lớp 7C có 50 học sinh. Hỏi dữ liệu trên có đại diện được cho mức độ yêu thích đối với việc đọc sách trong thư viện của các bạn học sinh lớp 7C hay không? Vì sao?
a) Dữ liệu định tính là dữ liệu không phải là số.
Dữ liệu định lượng là dữ liệu số.
b) Nếu tổng số bạn nam tham gia khảo sát bằng số học sinh lớp 7C thì dữ liệu trên đại diện được mức độ yêu thích đối với việc đọc sách trong thư viện của các bạn học sinh lớp 7C.
a)
- Dữ liệu định tính là: sở thích (không thích, thích, rất thích, không quan tâm)
- Dữ liệu định lượng là: số bạn nam (5; 7; 6; 4)
b) Số bạn nam tham gia khảo sát là: 5 + 7 + 6 + 4 = 22 (học sinh). Vì số học sinh lớp 7C là 50 học sinh nên dữ liệu trên chưa có đại diện được cho mức độ yêu thích đối với việc đọc sách trong thư viện của các bạn học sinh lớp 7C vì đối tượng khảo sát còn thiếu các bạn nữ.
Một người luyện tập chạy bộ từ nhà đến một công viên ở cách đó 874,8 m đường bộ với tốc độ là 97,2 (m/phút). Khi đến công viên, người này đã ở đây trong 10 phút để chơi cầu lông cùng nhóm bạn. Sau đó người này đã chạy bộ theo đường cũ từ công viên về nhà và dừng lại tại một quán cà phê cách nhà 360 m đường bộ. Biết rằng tổng thời gian từ lúc bắt đầu chạy bộ từ nhà cho đến khi dừng ở quán cà phê là 34,6 phút và quán này nằm trên đoạn đường từ nhà đến công viên. Hỏi khi chạy bộ từ công viên đến quán cà phê, tốc độ của người đó là bao nhiêu? (đơn vị đo là m/phút)
- Tính thời gian người đó chạy bộ từ nhà đến công viên.
- Thời gian chạy bộ từ công viên đến quán cà phê.
- Tính tốc độ của người đó từ công viên đến quán cà phê.
Thời gian người đó chạy từ nhà đến công viên là: 874,8: 97,2 = 9 (phút)
Thời gian người đó chạy từ công viên đến quán cà phê là: 34,6 – (9 + 10) = 15,6 (phút)
Quãng đường người đó chạy bộ từ công viên đến quán cà phê là: 874,8 – 360 = 514,8 (m)
Tốc độ chạy bộ của người đó từ công viên đến quán cà phê là: 514,8 : 15,6 = 33 (m/phút)
Đề thi học kì 1 Toán 7 - Đề số 13 chương trình Kết nối tri thức là một bài kiểm tra quan trọng, đánh giá mức độ nắm vững kiến thức và kỹ năng giải toán của học sinh sau nửa học kỳ đầu tiên. Đề thi bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính như số hữu tỉ, số thực, biểu thức đại số, phương trình bậc nhất một ẩn, bất đẳng thức và các ứng dụng thực tế.
Đề thi thường được chia thành các phần sau:
Các bài tập về số hữu tỉ và số thực thường yêu cầu học sinh:
Các bài tập về biểu thức đại số thường yêu cầu học sinh:
Các bài tập về phương trình bậc nhất một ẩn thường yêu cầu học sinh:
Các bài tập về bất đẳng thức thường yêu cầu học sinh:
Ví dụ 1: Giải phương trình 2x + 3 = 7
Lời giải:
Kết luận: Phương trình có nghiệm x = 2
Ví dụ 2: Tìm tập nghiệm của bất đẳng thức 3x - 1 > 5
Lời giải:
Kết luận: Tập nghiệm của bất đẳng thức là x > 2
Để chuẩn bị tốt nhất cho kỳ thi học kì 1, các em có thể tham khảo các tài liệu sau:
Đề thi học kì 1 Toán 7 - Đề số 13 - Kết nối tri thức là cơ hội để các em thể hiện những kiến thức và kỹ năng đã học. Hãy ôn tập kỹ lưỡng và tự tin làm bài để đạt kết quả tốt nhất. Chúc các em thành công!