Chào mừng các em học sinh lớp 7 đến với đề thi học kì 1 môn Toán chương trình Kết nối tri thức - Đề số 18.
Đề thi này được thiết kế bám sát chương trình học, giúp các em làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán!
Trong các số sau, số nào không là số hữu tỉ?
\( - \frac{5}{0}\).
\(\frac{4}{3}\).
\(\frac{0}{{ - 4}}\).
\( - 1\).
Cho \(\frac{a}{b}\) với \(a \in \mathbb{Z}\); b cần có thêm điều kiện gì để \(\frac{a}{b}\) là số hữu tỉ?
\(b \ne 0\).
\(b \in \mathbb{Z}\).
\(b \in \mathbb{N},b = 0\).
\(b \in \mathbb{Z},b \ne 0\).
Cho \(\Delta ABC\) vuông tại A, \(\widehat B = 55^\circ \). Số đo của góc C bằng:
\(35^\circ \).
\(55^\circ \).
\(145^\circ \).
\(90^\circ \).
Góc tạo bởi hai tia phân giác của hai góc kề bù bằng:
\(180^\circ \).
\(60^\circ \).
\(90^\circ \).
\(45^\circ \).
Đường thẳng d là trung trực của đoạn thẳng MN khi
d đi qua điểm I của MN.
\(d \bot MN\).
\(d \bot MN\) tại I và IM = IN.
\(d//MN\) và IM = IN.
Cho hai tam giác MNP và DEF có: \(MN = DE\); \(MP = DF\); \(NP = EF\); \(\widehat M = \widehat D\); \(\widehat N = \widehat E\); \(\widehat P = \widehat F\). Ta có:
\(\Delta MNP = \Delta DEF\).
\(\Delta MPN = \Delta EDF\).
\(\Delta NPM = \Delta DFE\).
Cả 3 đều đúng.
Căn bậc hai số học của 64 bằng
8.
16.
32.
64.
Chọn khẳng định đúng:
\(\left| { - 5,\left( 2 \right)} \right| = 5,2\).
\(\left| { - 5,\left( 2 \right)} \right| = - 5,\left( 2 \right)\).
\(\left| { - 5,\left( 2 \right)} \right| = 5,\left( 2 \right)\).
\(\left| { - 5,\left( 2 \right)} \right| = - 5,2\).
Với \(\sqrt {11} = 3,31662497...\). Chọn khẳng định đúng (làm tròn đến chữ số thập phân thứ 2)
\(\sqrt {11} \approx 3,33\).
\(\sqrt {11} \approx 3,32\).
\(\sqrt {11} \approx 3,31\).
\(\sqrt {11} \approx 3,3\).
Cho biểu đồ:
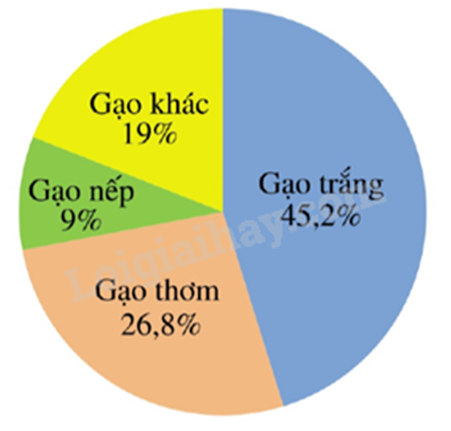
Hãy cho biết đây là dạng biểu đồ nào?
Biểu đồ tranh.
Biểu đồ đoạn thẳng.
Biểu đồ cột.
Biểu đồ hình quạt tròn.
Biểu đồ đoạn thẳng ở hình bên dưới biểu diễn số lượt khách vào một của hàng trong ngày đầu khai trương tại một số mốc thời gian:
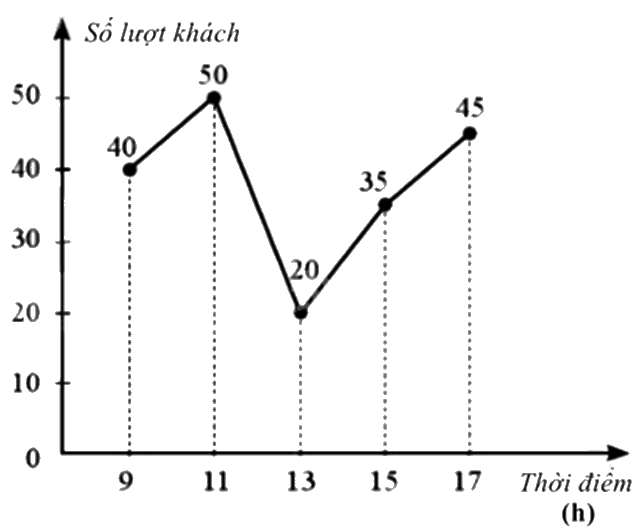
Vào thời điểm nào thì số lượt khách đến nhiều nhất?
9h.
11h.
13h.
17h.
Cho biểu đồ biểu diễn số huy chương của Đoàn thể thao Việt Nam và Đoàn thể thao Thái Lan tại Sea Game 30. Quan sát biểu đồ sau và chọn khẳng định sai?
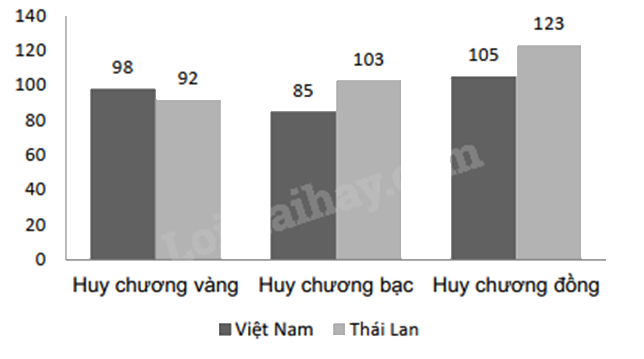
Huy chương vàng của Việt Nam nhiều hơn của Thái Lan.
Biểu đồ biểu diễn số lượng huy chương của Đoàn thể thao Việt Nam và Đoàn thể thao Thái Lan tại Sea Game 30.
Số lượng huy chương vàng của Việt Nam nhiều hơn của Thái Lan là 6.
Tổng số huy chương của Việt Nam nhiều hơn của Thái Lan.
Thực hiện phép tính:
a) \(\frac{{15}}{{39}}.\left( { - \frac{3}{5}} \right)\)
b) \(\frac{1}{3} - \frac{1}{3}.\left( {2 - \frac{3}{5}} \right)\)
c) \(\frac{{{9^{15}}{{.8}^{11}}}}{{{3^{29}}{{.16}^8}}}\)
d) \(\sqrt {\frac{{16}}{{49}}} + {\left( { - \frac{1}{2}} \right)^3} - \left| { - \frac{4}{7}} \right| - \frac{7}{8}\)
Tìm x, biết:
a) \(x + \sqrt {36} = 5\)
b) \(\left| {x - 2} \right| - \frac{3}{5} = \frac{1}{2}\)
Cho \(\Delta ABC\) cân tại A và M là trung điểm của BC. Gọi N là trung điểm của AB, trên tia đối của NC lấy điểm K sao cho \(NK = NC\). Chứng minh rằng:
a) \(\Delta ABM = \Delta ACM\).
b) \(AM \bot BC\).
c) \(AK = 2.MB\).
d) \(KA \bot AM\).
So sánh A và B, biết: \(A = \frac{{{{2024}^{2024}} + 1}}{{{{2024}^{2025}} + 1}}\); \(B = \frac{{{{2024}^{2023}} + 1}}{{{{2024}^{2024}} + 1}}\).
Trong các số sau, số nào không là số hữu tỉ?
\( - \frac{5}{0}\).
\(\frac{4}{3}\).
\(\frac{0}{{ - 4}}\).
\( - 1\).
Đáp án : A
Số hữu tỉ là số viết được dưới dạng phân số \(\frac{a}{b}\) (\(a,b \in \mathbb{Z};b \ne 0\)).
Số \( - \frac{5}{0}\) không phải số hữu tỉ vì mẫu số bằng 0.
Đáp án A
Cho \(\frac{a}{b}\) với \(a \in \mathbb{Z}\); b cần có thêm điều kiện gì để \(\frac{a}{b}\) là số hữu tỉ?
\(b \ne 0\).
\(b \in \mathbb{Z}\).
\(b \in \mathbb{N},b = 0\).
\(b \in \mathbb{Z},b \ne 0\).
Đáp án : D
Số hữu tỉ là số viết được dưới dạng phân số \(\frac{a}{b}\) (\(a,b \in \mathbb{Z};b \ne 0\)).
Để \(\frac{a}{b}\) là số hữu tỉ thì \(a,b \in \mathbb{Z};b \ne 0\) nên ta cần thêm điều kiện của b là \(b \in \mathbb{Z},b \ne 0\).
Đáp án D
Cho \(\Delta ABC\) vuông tại A, \(\widehat B = 55^\circ \). Số đo của góc C bằng:
\(35^\circ \).
\(55^\circ \).
\(145^\circ \).
\(90^\circ \).
Đáp án : A
Áp dụng tính chất tổng ba góc trong một tam giác bằng \(180^\circ \).
Tam giác ABC có:
\(\widehat A + \widehat B + \widehat C = 180^\circ \)
Suy ra \(\widehat C = 180^\circ - \widehat A - \widehat B = 180^\circ - 90^\circ - 55^\circ = 35^\circ \)
Đáp án A
Góc tạo bởi hai tia phân giác của hai góc kề bù bằng:
\(180^\circ \).
\(60^\circ \).
\(90^\circ \).
\(45^\circ \).
Đáp án : C
Dựa vào đặc điểm 2 góc kề bù bằng \(180^\circ \) và tia phân giác của một góc chia góc đó thành hai góc bằng nhau.
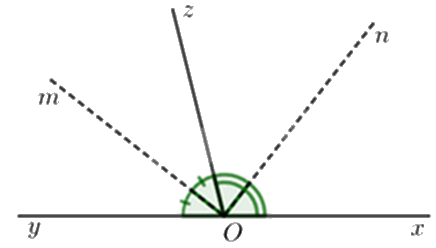
Hai góc kề bù có tổng số đo hai góc là \(180^\circ \).
Góc tạo bởi hai tia phân giác của hai góc kề bù bằng nửa tổng số đo của chúng:
\(\frac{1}{2}.180^\circ = 90^\circ \).
Đáp án C
Đường thẳng d là trung trực của đoạn thẳng MN khi
d đi qua điểm I của MN.
\(d \bot MN\).
\(d \bot MN\) tại I và IM = IN.
\(d//MN\) và IM = IN.
Đáp án : C
Đường thẳng vuông góc với 1 đoạn thẳng tại trung điểm của nó là đường trung trực của đoạn thẳng đó.
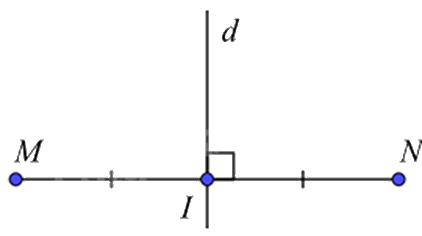
Đường thẳng d là trung trực của đoạn thẳng MN khi \(d \bot MN\) tại I và IM = IN.
Đáp án C
Cho hai tam giác MNP và DEF có: \(MN = DE\); \(MP = DF\); \(NP = EF\); \(\widehat M = \widehat D\); \(\widehat N = \widehat E\); \(\widehat P = \widehat F\). Ta có:
\(\Delta MNP = \Delta DEF\).
\(\Delta MPN = \Delta EDF\).
\(\Delta NPM = \Delta DFE\).
Cả 3 đều đúng.
Đáp án : A
Hai tam giác bằng nhau thì các góc và các cạnh tương ứng bằng nhau.
Hai tam giác MNP và DEF có: \(MN = DE\); \(MP = DF\); \(NP = EF\); \(\widehat M = \widehat D\); \(\widehat N = \widehat E\); \(\widehat P = \widehat F\) nên các đỉnh tương ứng là: M và D, N và E, P và F. Do đó \(\Delta MNP = \Delta DEF\).
Đáp án A
Căn bậc hai số học của 64 bằng
8.
16.
32.
64.
Đáp án : A
Căn bậc hai số học của một số a không âm là số x không âm sao cho \({x^2} = a\).
Căn bậc hai số học của 64 là: \(\sqrt {64} = 8\).
Đáp án A
Chọn khẳng định đúng:
\(\left| { - 5,\left( 2 \right)} \right| = 5,2\).
\(\left| { - 5,\left( 2 \right)} \right| = - 5,\left( 2 \right)\).
\(\left| { - 5,\left( 2 \right)} \right| = 5,\left( 2 \right)\).
\(\left| { - 5,\left( 2 \right)} \right| = - 5,2\).
Đáp án : C
Sử dụng kiến thức về giá trị tuyệt đối của một số:
+ Giá trị tuyệt đối của một số dương là chính nó
+ Giá trị tuyệt đối của một số âm là số đối của nó
Ta có: \(\left| { - 5,\left( 2 \right)} \right| = 5,\left( 2 \right)\).
Đáp án C
Với \(\sqrt {11} = 3,31662497...\). Chọn khẳng định đúng (làm tròn đến chữ số thập phân thứ 2)
\(\sqrt {11} \approx 3,33\).
\(\sqrt {11} \approx 3,32\).
\(\sqrt {11} \approx 3,31\).
\(\sqrt {11} \approx 3,3\).
Đáp án : B
Áp dụng quy tắc Làm tròn số thập phân dương:
- Đối với chữ số hàng làm tròn:
+ Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn 5;
+ Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hoặc bằng 5.
- Đối với chữ số sau hàng làm tròn:
+ Bỏ đi nếu ở phần thập phân;
+ Thay bằng các chữ số 0 nếu ở phần số nguyên.
Số \(\sqrt {11} = 3,31662497...\) làm tròn đến chữ số thập phân thứ hai là \(3,32\) vì chữ sao sau nó là số 6 > 5.
Đáp án B
Cho biểu đồ:
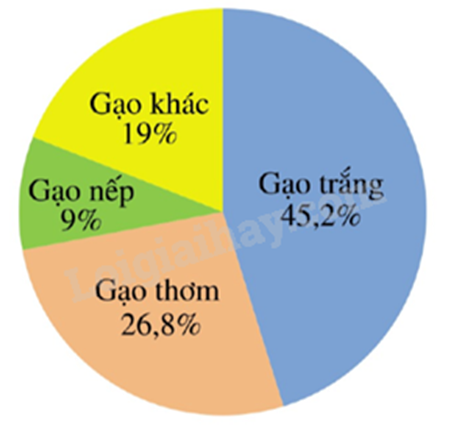
Hãy cho biết đây là dạng biểu đồ nào?
Biểu đồ tranh.
Biểu đồ đoạn thẳng.
Biểu đồ cột.
Biểu đồ hình quạt tròn.
Đáp án : D
Quan sát xem biểu đồ này là biểu đồ gì.
Biểu đồ trong hình là dạng biểu đồ hình quạt tròn.
Đáp án D
Biểu đồ đoạn thẳng ở hình bên dưới biểu diễn số lượt khách vào một của hàng trong ngày đầu khai trương tại một số mốc thời gian:
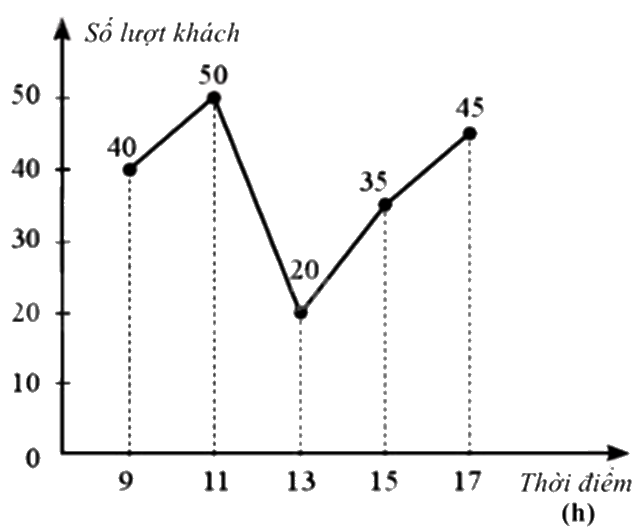
Vào thời điểm nào thì số lượt khách đến nhiều nhất?
9h.
11h.
13h.
17h.
Đáp án : B
Quan sát biểu đồ xem điểm biểu diễn thời điểm nào cao nhất thì số lượt khách đến nhiều nhất.
Ta thấy thời điểm 11h có số lượt khách đến nhiều nhất (50 lượt)
Đáp án B
Cho biểu đồ biểu diễn số huy chương của Đoàn thể thao Việt Nam và Đoàn thể thao Thái Lan tại Sea Game 30. Quan sát biểu đồ sau và chọn khẳng định sai?
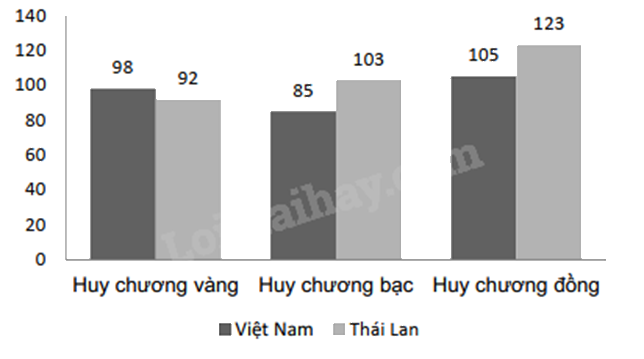
Huy chương vàng của Việt Nam nhiều hơn của Thái Lan.
Biểu đồ biểu diễn số lượng huy chương của Đoàn thể thao Việt Nam và Đoàn thể thao Thái Lan tại Sea Game 30.
Số lượng huy chương vàng của Việt Nam nhiều hơn của Thái Lan là 6.
Tổng số huy chương của Việt Nam nhiều hơn của Thái Lan.
Đáp án : D
Kiểm tra từng khẳng định xem khẳng định đó đúng hay sai.
Quan sát biểu đồ ta thấy:
Huy chương vàng của Việt Nam nhiều hơn của Thái Lan (98 > 92) nên A đúng.
Biểu đồ biểu diễn số lượng huy chương của Đoàn thể thao Việt Nam và Đoàn thể thao Thái Lan tại Sea Game 30 nên B đúng.
Số lượng huy chương vàng của Việt Nam nhiều hơn của Thái Lan là: 98 – 92 = 6 nên C đúng.
Tổng số huy chương của Việt Nam là: 98 + 85 + 105 = 288
Tổng số huy chương của Thái Lan là: 92 + 103 + 123 = 318
Vì 288 < 318 nên tổng số huy chương của Việt Nam ít hơn của Thái Lan. Vậy khẳng định D sai.
Đáp án D
Thực hiện phép tính:
a) \(\frac{{15}}{{39}}.\left( { - \frac{3}{5}} \right)\)
b) \(\frac{1}{3} - \frac{1}{3}.\left( {2 - \frac{3}{5}} \right)\)
c) \(\frac{{{9^{15}}{{.8}^{11}}}}{{{3^{29}}{{.16}^8}}}\)
d) \(\sqrt {\frac{{16}}{{49}}} + {\left( { - \frac{1}{2}} \right)^3} - \left| { - \frac{4}{7}} \right| - \frac{7}{8}\)
a, b: Thực hiện phép tính với số hữu tỉ.
c) Đưa các lũy thừa về cùng cơ số để rút gọn tử và mẫu số.
d) Tính căn bậc hai, lũy thừa và giá trị tuyệt đối sau đó thực hiện phép tính với số hữu tỉ.
a) \(\frac{{15}}{{39}}.\left( { - \frac{3}{5}} \right) = \frac{{15.\left( { - 3} \right)}}{{39.5}} = \frac{{ - 3}}{{13}}\)
b) \(\frac{1}{3} - \frac{1}{3}.\left( {2 - \frac{3}{5}} \right) = \frac{1}{3}\left( {1 - 2 + \frac{3}{5}} \right) = \frac{1}{3}.\frac{{ - 2}}{5} = \frac{{ - 2}}{{15}}\)
c) \(\frac{{{9^{15}}{{.8}^{11}}}}{{{3^{29}}{{.16}^8}}}\)\( = \frac{{{{\left( {{3^2}} \right)}^{15}}.{{\left( {{2^3}} \right)}^{11}}}}{{{3^{29}}.{{\left( {{2^4}} \right)}^8}}} = \frac{{{3^{30}}{{.2}^{33}}}}{{{3^{29}}{{.2}^{32}}}} = 3.2 = 6\)
d) \(\sqrt {\frac{{16}}{{49}}} + {\left( { - \frac{1}{2}} \right)^3} - \left| { - \frac{4}{7}} \right| - \frac{7}{8}\)
\(\begin{array}{l} = \frac{4}{7} - \frac{1}{8} - \frac{4}{7} - \frac{7}{8}\\ = \left( {\frac{4}{7} - \frac{4}{7}} \right) - \left( {\frac{1}{8} + \frac{7}{8}} \right)\\ = 0 - 1 = - 1\end{array}\)
Tìm x, biết:
a) \(x + \sqrt {36} = 5\)
b) \(\left| {x - 2} \right| - \frac{3}{5} = \frac{1}{2}\)
Áp dụng quy tắc chuyển vế đổi dấu.
b) Đưa về dạng \(\left| A \right| = B\), chia hai trường hợp: A = B hoặc A = -B.
a) \(x + \sqrt {36} = 5\)
\(\begin{array}{l}x + 6 = 5\\x = 5 - 6\\x = - 1\end{array}\)
Vậy \(x = - 1\).
b) \(\left| {x - 2} \right| - \frac{3}{5} = \frac{1}{2}\)
\(\begin{array}{l}\left| {x - 2} \right| = \frac{1}{2} + \frac{3}{5}\\\left| {x - 2} \right| = \frac{{11}}{{10}}\end{array}\)
\(x - 2 = \frac{{11}}{{10}}\) hoặc \(x - 2 = - \frac{{11}}{{10}}\)
\(x = \frac{{11}}{{10}} + 2\) \(x = - \frac{{11}}{{10}} + 2\)
\(x = \frac{{31}}{{10}}\) \(x = \frac{9}{{10}}\)
Vậy \(x \in \left\{ {\frac{{31}}{{10}};\frac{9}{{10}}} \right\}\).
Cho \(\Delta ABC\) cân tại A và M là trung điểm của BC. Gọi N là trung điểm của AB, trên tia đối của NC lấy điểm K sao cho \(NK = NC\). Chứng minh rằng:
a) \(\Delta ABM = \Delta ACM\).
b) \(AM \bot BC\).
c) \(AK = 2.MB\).
d) \(KA \bot AM\).
a) Chứng minh \(\Delta ABM = \Delta ACM\) theo trường hợp cạnh – cạnh – cạnh.
b) Chứng minh \(\widehat {AMB} = \widehat {AMC}\) và \(\widehat {AMB} + \widehat {AMC} = 180^\circ \) suy ra \(AM \bot BC\).
c) Chứng minh AK = BC và BC = 2MB nên AK = 2MB.
d) Chứng minh hai góc so le trong \(\widehat {KAN} = \widehat {CBN}\) nên AK // BC, mà \(AM \bot BC\) nên \(AK \bot AM\).
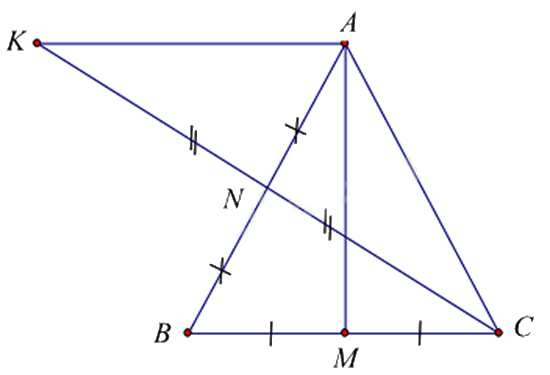
a) Xét \(\Delta ABM\) và \(\Delta ACM\) có:
AB = AC (gt)
AM là cạnh chung
BM = CM (gt)
Suy ra \(\Delta ABM = \Delta ACM\) (c.c.c)
b) Vì \(\Delta ABM = \Delta ACM\) (cmt) suy ra \(\widehat {AMB} = \widehat {AMC}\) (hai góc tương ứng).
Mà hai góc này là hai góc kề bù nên \(\widehat {AMB} + \widehat {AMC} = 180^\circ \), suy ra \(\widehat {AMB} = \widehat {AMC} = \frac{{180^\circ }}{2} = 90^\circ \) hay \(AM \bot BC\). (1)
c) Xét \(\Delta ANK\) và \(\Delta BNC\) có:
NA = NB (gt)
\(\widehat {ANK} = \widehat {BNC}\) (hai góc đối đỉnh)
NK = NC (gt)
suy ra \(\Delta ANK = \Delta BNC\) (c.g.c)
suy ra \(AK = BC\) (hai cạnh tương ứng).
Mà BC = 2.MB (vì M là trung điểm của BC)
Suy ra AK = 2.MB.
d) Vì \(\Delta ANK = \Delta BNC\) nên \(\widehat {KAN} = \widehat {CBN}\) (hai góc tương ứng)
Mà hai góc này nằm ở vị trí so le trong. Do đó AK // BC (2)
Từ (1) và (2) suy ra \(AK \bot AM\).
So sánh A và B, biết: \(A = \frac{{{{2024}^{2024}} + 1}}{{{{2024}^{2025}} + 1}}\); \(B = \frac{{{{2024}^{2023}} + 1}}{{{{2024}^{2024}} + 1}}\).
Áp dụng: nếu \(\frac{a}{b} < 1\) thì \(\frac{a}{b} < \frac{{a + m}}{{b + m}}\left( {a,b,m \in {\mathbb{N}^*}} \right)\)
Vì \(A = \frac{{{{2024}^{2024}} + 1}}{{{{2024}^{2025}} + 1}} < 1\) nên
\(\begin{array}{l}A = \frac{{{{2024}^{2024}} + 1}}{{{{2024}^{2025}} + 1}} < \frac{{{{2024}^{2024}} + 1 + 2023}}{{{{2024}^{2025}} + 1 + 2023}}\\ = \frac{{{{2024}^{2024}} + 2024}}{{{{2024}^{2025}} + 2024}} = \frac{{2024\left( {{{2024}^{2023}} + 1} \right)}}{{2024\left( {{{2024}^{2024}} + 1} \right)}}\\ = \frac{{{{2024}^{2023}} + 1}}{{{{2024}^{2024}} + 1}} = B\end{array}\)
Vậy A < B
Đề thi học kì 1 Toán 7 Kết nối tri thức - Đề số 18 là một bài kiểm tra quan trọng giúp đánh giá mức độ nắm vững kiến thức của học sinh sau một học kì học tập. Đề thi bao gồm các dạng bài tập khác nhau, từ trắc nghiệm đến tự luận, tập trung vào các chủ đề chính đã được học trong chương trình Kết nối tri thức.
Đề thi thường bao gồm các nội dung sau:
Cấu trúc đề thi có thể thay đổi tùy theo từng trường và từng giáo viên. Tuy nhiên, nhìn chung, đề thi thường được chia thành các phần sau:
Để đạt kết quả tốt trong kỳ thi học kì 1 Toán 7, học sinh cần:
Bài 1: (Trắc nghiệm) Chọn đáp án đúng:
Cho biểu thức A = 2x + 3y. Tính giá trị của A khi x = 1 và y = 2.
Hướng dẫn giải: Thay x = 1 và y = 2 vào biểu thức A, ta có: A = 2(1) + 3(2) = 2 + 6 = 8. Vậy đáp án đúng là B.
Để chuẩn bị tốt hơn cho kỳ thi học kì 1, học sinh có thể tham khảo các tài liệu sau:
Hãy dành thời gian ôn tập và luyện tập đầy đủ trước kỳ thi. Giữ tâm lý thoải mái và tự tin khi làm bài. Chúc các em đạt kết quả tốt nhất!
| Chủ đề | Kiến thức trọng tâm |
|---|---|
| Số học | Các phép toán, tính chất, quy tắc. |
| Biểu thức đại số | Thu gọn, tính giá trị, các phép toán. |
| Phương trình | Giải phương trình, ứng dụng. |
| Hình học | Các khái niệm, tính chất, công thức. |