Giaitoan.edu.vn xin giới thiệu Đề thi giữa kì 1 Toán 7 Kết nối tri thức - Đề số 11, một công cụ hữu ích giúp học sinh ôn luyện và đánh giá năng lực bản thân trước kỳ thi quan trọng.
Đề thi được biên soạn bám sát chương trình học, bao gồm các dạng bài tập khác nhau, từ cơ bản đến nâng cao, giúp học sinh làm quen với cấu trúc đề thi thực tế.
Cùng với đề thi, chúng tôi cung cấp đáp án chi tiết và lời giải bài tập, giúp học sinh tự học hiệu quả và hiểu sâu kiến thức.
Trong các số sau, số nào không phải là số hữu tỉ?
\( - 9\).
\(\sqrt {15} \).
\(\frac{2}{5}\).
\(2,5\).
Khẳng định nào dưới đây sai?
Số đối của 0 là 0.
Số đối của \(2\frac{1}{3}\) là \( - \frac{7}{3}\).
Số đối của 5 là \( - \left( { - 5} \right)\).
Số đối của -17 là 17.
Khẳng định nào dưới đây sai?
Căn bậc hai số học của 25 là 5.
Căn bậc hai số học của 0 là 0.
Căn bậc hai số học của 16 là - 4.
Căn bậc hai số học của 3 là \(\sqrt 3 \).
Cho hình vẽ bên, \(\widehat {BAH}\) và \(\widehat {CBE}\) là một cặp góc
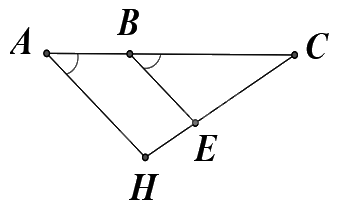
bù nhau.
trong cùng phía.
so le trong.
đồng vị.
Tiên đề Euclid được phát biểu:
“ Qua một điểm ở ngoài đường thẳng ....”
Có vô số đường thẳng song song với đường thẳng đó.
Có hai đường thẳng song song với đường thẳng đó.
Có hai đường thẳng song song với đường thẳng đó.
Chỉ có một đường thẳng song song với đường thẳng đó.
Đường thẳng d cắt hai đường thẳng song song a và b lần lượt tại hai điểm A, B như hình
vẽ. Khi đó kết luận nào sau đây là không đúng.
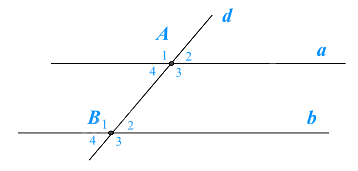
\(\widehat {{A_1}} + \widehat {{B_3}} = 180^\circ \).
\(\widehat {{A_1}} = \widehat {{B_1}}\).
\(\widehat {{A_1}} = \widehat {{A_3}}\).
\(\widehat {{A_1}} + \widehat {{B_4}} = 180^\circ \).
Giá trị của biểu thức \(P = \sqrt {100 - 36} + \sqrt {81} \) là:
\(13\).
\(4\).
\(17\).
\(9\).
Chọn câu đúng nhất: Hai góc đối đỉnh trong hình là:
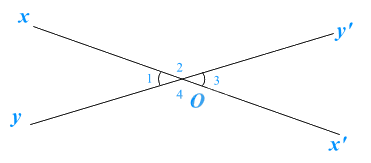
\(\widehat {{O_1}}\) và \(\widehat {{O_4}}\).
\(\widehat {{O_2}}\) và \(\widehat {{O_4}}\).
\(\widehat {{O_1}}\) và \(\widehat {{O_3}}\).
\(\widehat {{O_1}}\) và \(\widehat {{O_3}}\); \(\widehat {{O_2}}\) và \(\widehat {{O_4}}\).
Kết quả \({\left( { - \frac{2}{5}} \right)^3}\) là
\(\frac{8}{{125}}\).
\(\frac{4}{{25}}\).
\( - \frac{8}{{125}}\).
\(\frac{8}{{15}}\).
Cho \(\widehat {xOy} = 80^\circ \), \(Ot\) là tia phân giác của \(\widehat {xOy}\). Số đo \(\widehat {xOt}\) bằng?
\(160^\circ \).
\(30^\circ \).
\(35^\circ \).
\(40^\circ \).
So sánh hai số hữu tỉ \( - 0,2\) và \(\frac{{ - 2}}{5}\)
\( - 0,2 < \frac{{ - 2}}{5}\).
\( - 0,2 = \frac{{ - 2}}{5}\).
\( - 0,2 > \frac{{ - 2}}{5}\).
\( - 0,2 \ge \frac{{ - 2}}{5}\).
Kết quả của phép tính \(\left( {\frac{{11}}{{12}}:\frac{{33}}{{16}}} \right).\frac{3}{2}\) là
\(\frac{4}{9}\).
\(\frac{3}{2}\).
\(\frac{2}{3}\).
\(\frac{{15}}{4}\).
Thực hiện phép tính
a) \(0,2 + \frac{3}{5}:\frac{{ - 3}}{2}\);
b) \(\frac{4}{5}.\frac{3}{{13}} + 0,8.\frac{{10}}{{13}} - \frac{7}{5}\);
c) \(\frac{{{3^8}{{.3}^{18}}}}{{{{27}^5}{{.9}^6}}}\).
Tìm số hữu tỉ x, biết:
a) \(\frac{4}{5} - x = \frac{3}{4}\);
b) \(\frac{5}{6} + \frac{1}{{10}}:x = \frac{4}{5}\);
c) \({\left( {\frac{3}{5} - x} \right)^2} = \frac{9}{{25}}\).
Một cửa hàng có 160kg gạo và bán hết trong 3 ngày. Ngày thứ nhất cửa hàng bán được \(\frac{3}{8}\) số gạo. Ngày thứ hai cửa hàng bán được \(\frac{1}{4}\) số gạo còn lại. Tính tỉ số gạo bán được của ngày thứ ba và ngày thứ nhất.
Cho hình vẽ, biết \(\widehat {xFE} = 83^\circ \), \(\widehat {FEH} = 83^\circ \), \(\widehat {FGy} = 76^\circ \).
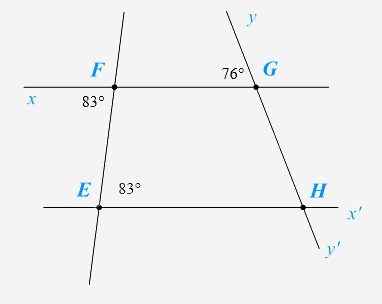
a) Chứng tỏ \(FG//EH\).
b) Hãy tính số đo góc x’Hy’.
Chứng minh rằng \(A = \frac{1}{3} + \frac{1}{{{3^2}}} + \frac{1}{{{3^3}}} + ... + \frac{1}{{{3^{2022}}}} + \frac{1}{{{3^{2023}}}} < \frac{1}{2}\)
Trong các số sau, số nào không phải là số hữu tỉ?
\( - 9\).
\(\sqrt {15} \).
\(\frac{2}{5}\).
\(2,5\).
Đáp án : B
Số hữu tỉ là các số viết được dưới dạng \(\frac{a}{b}\left( {a,b \in Z,b \ne 0} \right)\)
Số \(\sqrt {15} \) không phải là số hữu tỉ.
Đáp án B.
Khẳng định nào dưới đây sai?
Số đối của 0 là 0.
Số đối của \(2\frac{1}{3}\) là \( - \frac{7}{3}\).
Số đối của 5 là \( - \left( { - 5} \right)\).
Số đối của -17 là 17.
Đáp án : C
Số đối của số hữu tỉ a là – a.
Ta có: \( - \left( { - 5} \right) = 5\). Mà số đối của 5 là -5 nên đáp án C sai.
Đáp án C.
Khẳng định nào dưới đây sai?
Căn bậc hai số học của 25 là 5.
Căn bậc hai số học của 0 là 0.
Căn bậc hai số học của 16 là - 4.
Căn bậc hai số học của 3 là \(\sqrt 3 \).
Đáp án : C
Dựa vào khái niệm căn bậc hai số học: Căn bậc hai số học của một số a không âm, kí hiệu \(\sqrt a \), là số x không âm sao cho \({x^2} = a\).
Căn bậc hai số học của một số a là \(\sqrt a \) nên:
+ Căn bậc hai số học của 25 là \(\sqrt {25} = 5\).
+ Căn bậc hai số học của 0 là 0.
+ Căn bậc hai số học của 16 là \(\sqrt {16} = 4\) nên C sai.
+ Căn bậc hai số học của 3 là \(\sqrt 3 \).
Đáp án C.
Cho hình vẽ bên, \(\widehat {BAH}\) và \(\widehat {CBE}\) là một cặp góc
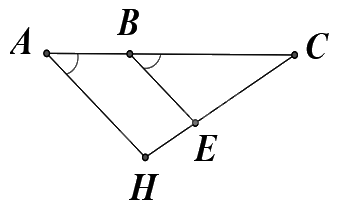
bù nhau.
trong cùng phía.
so le trong.
đồng vị.
Đáp án : D
Dựa vào kiến thức về các góc tạo bởi một đường thẳng cắt hai đường thẳng.
Cặp góc \(\widehat {BAH}\) và \(\widehat {CBE}\) là một cặp góc đồng vị.
Đáp án D.
Tiên đề Euclid được phát biểu:
“ Qua một điểm ở ngoài đường thẳng ....”
Có vô số đường thẳng song song với đường thẳng đó.
Có hai đường thẳng song song với đường thẳng đó.
Có hai đường thẳng song song với đường thẳng đó.
Chỉ có một đường thẳng song song với đường thẳng đó.
Đáp án : D
Chỉ có một đường thẳng song song với đường thẳng đó.
Tiên đề Euclid: Qua một điểm nằm ngoài một đường thẳng, chỉ có một đường thẳng song song với đường thẳng đó.
Đáp án D.
Đường thẳng d cắt hai đường thẳng song song a và b lần lượt tại hai điểm A, B như hình
vẽ. Khi đó kết luận nào sau đây là không đúng.
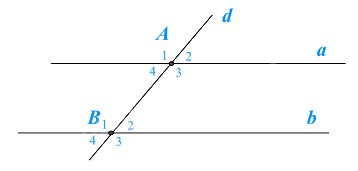
\(\widehat {{A_1}} + \widehat {{B_3}} = 180^\circ \).
\(\widehat {{A_1}} = \widehat {{B_1}}\).
\(\widehat {{A_1}} = \widehat {{A_3}}\).
\(\widehat {{A_1}} + \widehat {{B_4}} = 180^\circ \).
Đáp án : A
Sử dụng tính chất của hai đường thẳng song song, tính chất hai góc kề bù.
Vì đường thẳng d cắt hai đường thẳng song song a và b lần lượt tại hai điểm A, B nên \(\widehat {{A_1}} = \widehat {{B_1}}\) (hai góc đồng vị) nên B đúng.
Khi đó \(\widehat {{A_1}} + \widehat {{B_4}} = \widehat {{B_1}} + \widehat {{B_4}} = 180^\circ \) (vì \(\widehat {{B_1}}\) và \(\widehat {{B_4}}\) là hai góc kề bù) nên D đúng.
\(\widehat {{A_1}} = \widehat {{A_3}}\) vì là hai góc đối đỉnh nên C đúng.
Do đó đáp án A sai.
Đáp án A.
Giá trị của biểu thức \(P = \sqrt {100 - 36} + \sqrt {81} \) là:
\(13\).
\(4\).
\(17\).
\(9\).
Đáp án : C
Sử dụng kiến thức căn bậc hai của một số.
\(P = \sqrt {100 - 36} + \sqrt {81} = \sqrt {64} + \sqrt {81} = 8 + 9 = 17\).
Đáp án C.
Chọn câu đúng nhất: Hai góc đối đỉnh trong hình là:
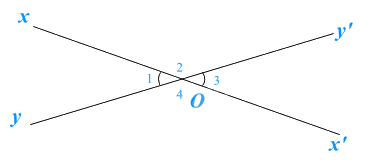
\(\widehat {{O_1}}\) và \(\widehat {{O_4}}\).
\(\widehat {{O_2}}\) và \(\widehat {{O_4}}\).
\(\widehat {{O_1}}\) và \(\widehat {{O_3}}\).
\(\widehat {{O_1}}\) và \(\widehat {{O_3}}\); \(\widehat {{O_2}}\) và \(\widehat {{O_4}}\).
Đáp án : D
Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
Trong hình trên có hai cặp góc đối đỉnh là \(\widehat {{O_1}}\) và \(\widehat {{O_3}}\); \(\widehat {{O_2}}\) và \(\widehat {{O_4}}\).
Đáp án D.
Kết quả \({\left( { - \frac{2}{5}} \right)^3}\) là
\(\frac{8}{{125}}\).
\(\frac{4}{{25}}\).
\( - \frac{8}{{125}}\).
\(\frac{8}{{15}}\).
Đáp án : C
Sử dụng \({\left( {\frac{x}{y}} \right)^n} = \frac{{{x^n}}}{{{y^n}}}\).
\({\left( { - \frac{2}{5}} \right)^3} = - {\left( {\frac{2}{5}} \right)^3} = \frac{{{2^3}}}{{{5^3}}} = - \frac{8}{{125}}\).
Đáp án C.
Cho \(\widehat {xOy} = 80^\circ \), \(Ot\) là tia phân giác của \(\widehat {xOy}\). Số đo \(\widehat {xOt}\) bằng?
\(160^\circ \).
\(30^\circ \).
\(35^\circ \).
\(40^\circ \).
Đáp án : D
Sử dụng tính chất tia phân giác của một góc.
Vì Ot là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOt} = \widehat {yOt} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.80^\circ = 40^\circ \)
Đáp án D.
So sánh hai số hữu tỉ \( - 0,2\) và \(\frac{{ - 2}}{5}\)
\( - 0,2 < \frac{{ - 2}}{5}\).
\( - 0,2 = \frac{{ - 2}}{5}\).
\( - 0,2 > \frac{{ - 2}}{5}\).
\( - 0,2 \ge \frac{{ - 2}}{5}\).
Đáp án : C
Đưa hai số về phân số và thực hiện so sánh.
Ta có: \( - 0,2 = \frac{{ - 2}}{{10}} = \frac{{ - 1}}{5}\).
Vì \(\frac{{ - 1}}{5} > \frac{{ - 2}}{5}\) nên \( - 0,2 > \frac{{ - 2}}{5}\).
Đáp án C.
Kết quả của phép tính \(\left( {\frac{{11}}{{12}}:\frac{{33}}{{16}}} \right).\frac{3}{2}\) là
\(\frac{4}{9}\).
\(\frac{3}{2}\).
\(\frac{2}{3}\).
\(\frac{{15}}{4}\).
Đáp án : C
Thực hiện lần lượt phép tính.
Ta có:
\(\left( {\frac{{11}}{{12}}:\frac{{33}}{{16}}} \right).\frac{3}{2} = \left( {\frac{{11}}{{12}}.\frac{{16}}{{33}}} \right).\frac{3}{2} = \frac{4}{9}.\frac{3}{2} = \frac{2}{3}\).
Đáp án C.
Thực hiện phép tính
a) \(0,2 + \frac{3}{5}:\frac{{ - 3}}{2}\);
b) \(\frac{4}{5}.\frac{3}{{13}} + 0,8.\frac{{10}}{{13}} - \frac{7}{5}\);
c) \(\frac{{{3^8}{{.3}^{18}}}}{{{{27}^5}{{.9}^6}}}\).
a), b) Sử dụng quy tắc tính với số hữu tỉ.
c) Sử dụng quy tắc nhân, chia lũy thừa cùng cơ số.
a) \(0,2 + \frac{3}{5}:\frac{{ - 3}}{2}\)
\(\begin{array}{l} = \frac{1}{5} + \frac{3}{5}.\frac{{ - 2}}{3}\\ = \frac{1}{5} + \frac{{ - 2}}{5}\\ = \frac{{ - 1}}{5}\end{array}\)
b) \(\frac{4}{5}.\frac{3}{{13}} + 0,8.\frac{{10}}{{13}} - \frac{7}{5}\)
\(\begin{array}{l} = \frac{4}{5}.\frac{3}{{13}} + \frac{4}{5}.\frac{{10}}{{13}} - \frac{7}{5}\\ = \frac{4}{5}\left( {\frac{3}{{13}} + \frac{{10}}{{13}}} \right) - \frac{7}{5}\\ = \frac{4}{5} - \frac{7}{5}\\ = \frac{{ - 3}}{5}\end{array}\)
c) \(\frac{{{3^8}{{.3}^{18}}}}{{{{27}^5}{{.9}^6}}}\)\( = \frac{{{3^8}{{.3}^{18}}}}{{{{\left( {{3^3}} \right)}^5}{{.3}^{12}}}} = \frac{{{3^{26}}}}{{{3^{27}}}} = \frac{1}{3}\)
Tìm số hữu tỉ x, biết:
a) \(\frac{4}{5} - x = \frac{3}{4}\);
b) \(\frac{5}{6} + \frac{1}{{10}}:x = \frac{4}{5}\);
c) \({\left( {\frac{3}{5} - x} \right)^2} = \frac{9}{{25}}\).
a), b) Sử dụng quy tắc tính với số hữu tỉ.
c) Sử dụng quy tắc nhân, chia lũy thừa cùng cơ số.
a) $\frac{4}{5}-x=\frac{3}{4}$
$ x=\frac{4}{5}-\frac{3}{4} $
$x=\frac{1}{20} $
Vậy $x=\frac{1}{20}$.
b) $\frac{5}{6}+\frac{1}{10}:x=\frac{4}{5}$
$ \frac{1}{10}:x=\frac{4}{5}-\frac{5}{6} $
$\frac{1}{10}:x=\frac{-1}{30}$
$ x=\frac{1}{10}:\frac{-1}{30} $
$ x=-3 $
Vậy $x=-3$
c) ${{\left( \frac{3}{5}-x \right)}^{2}}=\frac{9}{25}$
${{\left( \frac{3}{5}-x \right)}^{2}}={{\left( \frac{3}{5} \right)}^{2}}$
TH1: $\frac{3}{5}-x=\frac{3}{5}$
$ x=\frac{3}{5}-\frac{3}{5} $
$x=0 $
TH2: $\frac{3}{5}-x=-\frac{3}{5}$
$ x=\frac{3}{5}-\left( -\frac{3}{5} \right) $
$ x=\frac{6}{5} $
Vậy $x=0$; $x=\frac{6}{5}$.
Một cửa hàng có 160kg gạo và bán hết trong 3 ngày. Ngày thứ nhất cửa hàng bán được \(\frac{3}{8}\) số gạo. Ngày thứ hai cửa hàng bán được \(\frac{1}{4}\) số gạo còn lại. Tính tỉ số gạo bán được của ngày thứ ba và ngày thứ nhất.
Tính khối lượng gạo cửa hàng bán trong ngày thứ nhất, ngày thứ hai, ngày thứ ba.
Từ đó tính tỉ số gạo bán được của ngày thứ ba và ngày thứ nhất.
Khối lượng gạo cửa hàng bán trong ngày thứ nhất là:
\(\frac{3}{8}.160 = 60\left( {kg} \right)\)
Khối lượng gạo cửa hàng bán trong ngày thứ hai là:
\(\frac{1}{4}\left( {160 - 60} \right) = 25\left( {kg} \right)\)
Khối lượng gạo cửa hàng bán trong ngày thứ ba là:
\(160 - 60 - 25 = 75\left( {kg} \right)\)
Tỉ số gạo bán được của ngày thứ ba và ngày thứ nhất là:
\(\frac{{75}}{{60}} = \frac{5}{4}\).
Vậy tỉ số gạo bán được của ngày thứ ba và ngày thứ nhất là \(\frac{5}{4}\).
Cho hình vẽ, biết \(\widehat {xFE} = 83^\circ \), \(\widehat {FEH} = 83^\circ \), \(\widehat {FGy} = 76^\circ \).
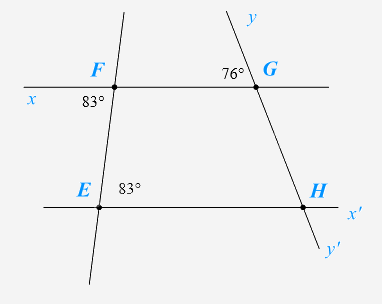
a) Chứng tỏ \(FG//EH\).
b) Hãy tính số đo góc x’Hy’.
a) Dựa vào dấu hiệu nhận biết hai đường thẳng song song.
b) Dựa vào tính chất của hai đường thẳng song song, hai góc đối đỉnh.
a) Ta có: \(\widehat {xFE} = 83^\circ \), \(\widehat {FEH} = 83^\circ \) nên \(\widehat {xFE} = \widehat {FEH}\).
Mà hai góc này là hai góc so le trong nên \(FG//EH\).
b) Ta có: \(FG//EH\) nên \(\widehat {FGy} = \widehat {EHG}\) (hai góc đồng vị)
Suy ra \(\widehat {EHG} = 76^\circ \).
Ta có: \(\widehat {x'Hy'} = \widehat {EHG} = 76^\circ \) (hai góc đối đỉnh)
Vậy \(\widehat {x'Hy'} = 76^\circ \).
Chứng minh rằng \(A = \frac{1}{3} + \frac{1}{{{3^2}}} + \frac{1}{{{3^3}}} + ... + \frac{1}{{{3^{2022}}}} + \frac{1}{{{3^{2023}}}} < \frac{1}{2}\)
Nhân cả hai vế của A với 3.
Tính 2A.
Suy ra giá trị của A, so sánh với \(\frac{1}{2}\).
Ta có:
\(3A = 3.\left( {\frac{1}{3} + \frac{1}{{{3^2}}} + \frac{1}{{{3^3}}} + ... + \frac{1}{{{3^{2022}}}} + \frac{1}{{{3^{2023}}}}} \right) = 1 + \frac{1}{3} + \frac{1}{{{3^2}}} + \frac{1}{{{3^3}}} + ... + \frac{1}{{{3^{2021}}}} + \frac{1}{{{3^{2022}}}}\)
Suy ra
\(\begin{array}{l}3A - A = 1 + \frac{1}{3} + \frac{1}{{{3^2}}} + \frac{1}{{{3^3}}} + ... + \frac{1}{{{3^{2021}}}} + \frac{1}{{{3^{2022}}}} - \left( {\frac{1}{3} + \frac{1}{{{3^2}}} + \frac{1}{{{3^3}}} + ... + \frac{1}{{{3^{2022}}}} + \frac{1}{{{3^{2023}}}}} \right)\\2A = 1 - \frac{1}{{{3^{2023}}}}\end{array}\)
Do đó \(A = \frac{1}{2}\left( {1 - \frac{1}{{{3^{2023}}}}} \right)\).
Mà \(1 - \frac{1}{{{3^{2023}}}} < 1\) nên \(A = \frac{1}{2}\left( {1 - \frac{1}{{{3^{2023}}}}} \right) < \frac{1}{2}.1 = \frac{1}{2}\) hay \(A < \frac{1}{2}\).
Đề thi giữa kì 1 Toán 7 Kết nối tri thức - Đề số 11 đóng vai trò quan trọng trong việc đánh giá mức độ nắm vững kiến thức của học sinh sau một nửa học kì. Đề thi này không chỉ kiểm tra khả năng vận dụng các công thức, định lý mà còn đánh giá khả năng giải quyết vấn đề và tư duy logic của học sinh. Bài viết này sẽ cung cấp thông tin chi tiết về cấu trúc đề thi, các dạng bài tập thường gặp và hướng dẫn giải chi tiết để giúp học sinh ôn tập hiệu quả.
Thông thường, đề thi giữa kì 1 Toán 7 Kết nối tri thức - Đề số 11 bao gồm các phần sau:
Các chủ đề thường xuất hiện trong đề thi bao gồm:
Dưới đây là một số dạng bài tập thường gặp trong đề thi giữa kì 1 Toán 7 Kết nối tri thức - Đề số 11:
Bài 1: Tính giá trị của biểu thức A = (1/2 + 1/3) * 6/5
Giải:
A = (3/6 + 2/6) * 6/5 = 5/6 * 6/5 = 1
Bài 2: Giải phương trình 2x + 3 = 7
Giải:
2x = 7 - 3 = 4
x = 4 / 2 = 2
Đề thi giữa kì 1 Toán 7 Kết nối tri thức - Đề số 11 là một cơ hội tốt để học sinh đánh giá năng lực và củng cố kiến thức. Bằng cách ôn tập kỹ lưỡng và luyện tập thường xuyên, học sinh có thể tự tin đạt kết quả tốt trong kỳ thi sắp tới. Chúc các em học sinh ôn tập tốt và đạt thành tích cao!