Chào mừng các em học sinh lớp 7 đến với đề thi giữa kì 2 môn Toán chương trình Kết nối tri thức - Đề số 7.
Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong học kì 2.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán!
Nếu4.b = 5.c và b, c ≠ 0 thì:
Nếu các số x, y, z tỉ lệ với các số 6; 4; 3 thì ta có dãy tỉ số bằng nhau nào:
Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ 5. Ta có:
Cho x và y là hai đại lượng tỉ lệ thuận với nhau. Biết hệ số tỉ lệ của x đối với y là 8. Hệ số tỉ lệ của y đối với x là:
Cho biết y và x là hai đại lượng tỉ lệ nghịch theo hệ số tỉ lệ a. Ta có:
Cho tam giác ABC. Trong các khẳng định sau khẳng định nào sai?
Trong các biểu thức sau, em hãy chỉ ra biểu thức số.
Biểu thức biểu thị số tiền An phải trả để mua \(x\) quyển sách với giá \(10000\) đồng là:
Cho tam giác ABC có: \(\widehat A = {45^0};\widehat B = {60^0}\). So sánh các cạnh của tam giác ABC là:
Biểu thức nào là đa thức một biến?
Bậc của đa thức \({x^3} + 2{x^2} + 3x - 5\) là
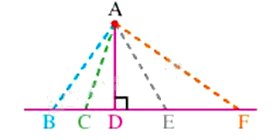
Cho hình vẽ, có bao nhiêu đường xiên kẻ từ điểm A đến đường thẳng BF?
1. Tìm x biết: \(\frac{x}{4} = \frac{7}{5}\).
2. Cho biết đại lượng x và y tỉ lệ thuận với nhau và khi x = 20 thì y = 12.
a) Tìm hệ số tỉ lệ của y đối với x và biểu diễn y theo x.
b) Tính giá trị của x khi \(y = \frac{{ - 1}}{3}\).
Ba lớp 7A, 7B, 7C thu tập tặng bạn vùng bão. Biết số vở của ba lớp lần lượt tỉ lệ với 3; 4; 5 và tổng số vở của lớp 7A và 7C là 240 cuốn. Tính số vở của mỗi lớp thu được.
Một đội công nhân có 15 người làm xong công việc trong 90 ngày. Hỏi cần bổ sung thêm bao nhiêu công nhân để hoàn thành công việc đó chỉ trong 50 ngày.
So sánh các cạnh của tam giác ABC có \(\widehat A = {50^0},\,\widehat B = {60^0}\).
Cho tam giác ABC có AB = AC, N là trung điểm của BC.
a) Chứng minh \(\Delta ABN = \Delta ACN\).
b) Qua A kẻ đường thẳng a vuông góc với AN. Chứng minh a // BC.
c) Vẽ điểm F sao cho N là trung điểm của AF. Chứng minh AB + AC > 2AN.
Nếu4.b = 5.c và b, c ≠ 0 thì:
Đáp án : B
Dựa vào tính chất của tỉ lệ thức: Nếu \(ad = bc\left( {a,b,c,d \ne 0} \right)\) thì ta có các tỉ lệ thức:
\(\frac{a}{b} = \frac{c}{d};\frac{a}{c} = \frac{b}{d};\frac{d}{b} = \frac{c}{a};\frac{d}{c} = \frac{b}{a}\)
Nếu \(4.b = 5.c\) thì ta có các tỉ lệ thức:
\(\frac{4}{c} = \frac{5}{b};\frac{4}{5} = \frac{c}{b};\frac{c}{4} = \frac{b}{5};\frac{5}{4} = \frac{b}{c}\) nên B đúng.
Nếu các số x, y, z tỉ lệ với các số 6; 4; 3 thì ta có dãy tỉ số bằng nhau nào:
Đáp án : D
Dựa vào tính chất dãy tỉ số bằng nhau.
Nếu các số x, y, z tỉ lệ với các số 6; 4; 3 thì ta có dãy tỉ số bằng nhau:
\(\frac{x}{6} = \frac{y}{4} = \frac{z}{3}\).
Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ 5. Ta có:
Đáp án : A
Dựa vào kiến thức về hai đại lượng tỉ lệ thuận.
Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ 5 ta có công thức \(y = 5x\).
Cho x và y là hai đại lượng tỉ lệ thuận với nhau. Biết hệ số tỉ lệ của x đối với y là 8. Hệ số tỉ lệ của y đối với x là:
Đáp án : B
Khi đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ k (khác 0) thì x cũng tỉ lệ thuận với y theo hệ số tỉ lệ \(\frac{1}{k}\) và ta nói hai đại lượng đó tỉ lệ thuận với nhau.
Hệ số tỉ lệ của x đối với y là 8 nên hệ số tỉ lệ của y đối với x là \(\frac{1}{8}\).
Cho biết y và x là hai đại lượng tỉ lệ nghịch theo hệ số tỉ lệ a. Ta có:
Đáp án : B
Dựa vào kiến thức về hai đại lượng tỉ lệ nghịch.
Nếu y và x là hai đại lượng tỉ lệ nghịch theo hệ số tỉ lệ a thì \(y = \frac{a}{x}\) hay \(xy = a\).
Cho tam giác ABC. Trong các khẳng định sau khẳng định nào sai?
Đáp án : C
Dựa vào quan hệ giữa ba cạnh của một tam giác.
Trong một tam giác, tổng độ dài hai cạnh bất kỳ bao giờ cũng lớn hơn độ dài cạnh còn lại nên A, B và D đúng.
Trong một tam giác, hiệu độ dài hai cạnh bất kỳ bao giờ cũng nhỏ hơn độ dài cạnh còn lại nên C sai.
Trong các biểu thức sau, em hãy chỉ ra biểu thức số.
Đáp án : B
Dựa vào các kiến thức về biểu thức số.
Trong các biểu thức trên, biểu thức số là biểu thức \(2 - (3.4 + 5)\).
Biểu thức biểu thị số tiền An phải trả để mua \(x\) quyển sách với giá \(10000\) đồng là:
Đáp án : A
Dựa vào các kiến thức về biểu thức đại số.
Biểu thức biểu thị số tiền An phải trả để mua \(x\) quyển sách với giá \(10000\) đồng là:
\(10000.x\)
Cho tam giác ABC có: \(\widehat A = {45^0};\widehat B = {60^0}\). So sánh các cạnh của tam giác ABC là:
Đáp án : A
Áp dụng định lí tổng ba góc của một tam giác và quan hệ giữa góc và cạnh đối diện trong một tam giác.
Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^0}\\\widehat C = {180^0} - \widehat A - \widehat B\\ = {180^0} - {45^0} - {60^0}\\ = {75^0}\end{array}\)
Trong tam giác ABC, ta có:
\(\widehat C > \widehat B > \widehat A\left( {{{75}^0} > {{60}^0} > {{45}^0}} \right)\) suy ra \(AB > AC > BC\).
Biểu thức nào là đa thức một biến?
Đáp án : A
Dựa vào kiến thức về đa thức một biến.
Biểu thức một biến là \( - {y^2} + 3y + 5\).
Bậc của đa thức \({x^3} + 2{x^2} + 3x - 5\) là
Đáp án : D
Dựa vào kiến thức về bậc của đa thức một biến.
Bậc của đa thức \({x^3} + 2{x^2} + 3x - 5\) là 3.
Cho hình vẽ, có bao nhiêu đường xiên kẻ từ điểm A đến đường thẳng BF?
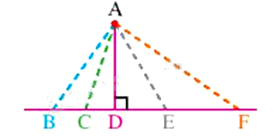
Đáp án : D
Dựa vào kiến thức về đường xiên.
Trong hình trên, có 4 đường xiên là: AB, AC, AE, AF.
1. Tìm x biết: \(\frac{x}{4} = \frac{7}{5}\).
2. Cho biết đại lượng x và y tỉ lệ thuận với nhau và khi x = 20 thì y = 12.
a) Tìm hệ số tỉ lệ của y đối với x và biểu diễn y theo x.
b) Tính giá trị của x khi \(y = \frac{{ - 1}}{3}\).
1. Dựa vào tính chất của tỉ lệ thức để tìm x.
2. Sử dụng kiến thức về hai đại lượng tỉ lệ thuận với nhau.
1. Ta có:
\(\begin{array}{l}\frac{x}{4} = \frac{7}{5}\\5x = 7.4\\5x = 28\\x = \frac{{28}}{5}\end{array}\)
Vậy \(x = \frac{{28}}{5}\).
2.
a) Vì đại lượng x và y tỉ lệ thuận với nhau nên \(y = kx\) (\(k \ne 0\))
Vì khi x = 20 thì y = 12 nên \(20 = k.12\) suy ra \(k = \frac{{20}}{{12}} = \frac{5}{3}\).
Vậy hệ số tỉ lệ của y đối với x là \(k = \frac{5}{3}\) và \(y = \frac{5}{3}x\).
b) Thay \(y = \frac{{ - 1}}{3}\) vào công thức ta được: \(\frac{{ - 1}}{3} = \frac{5}{3}x\) suy ra \(x = \frac{{ - 1}}{5}\).
Ba lớp 7A, 7B, 7C thu tập tặng bạn vùng bão. Biết số vở của ba lớp lần lượt tỉ lệ với 3; 4; 5 và tổng số vở của lớp 7A và 7C là 240 cuốn. Tính số vở của mỗi lớp thu được.
Áp dụng tính chất của dãy tỉ số bằng nhau để tìm số vở của mỗi lớp thu được.
Gọi số vở lớp 7A, 7B, 7C lần lượt là a, b, c \(\left( {a,b,c \in \mathbb{N}*} \right)\) (cuốn)
Vì số học sinh lớp 7A, 7B, 7C tương ứng tỉ lệ với 3; 4; 5 nên ta có dãy tỉ số bằng nhau:
\(\frac{a}{3} = \frac{b}{4} = \frac{c}{5}\)
Do tổng số vở của lớp 7A và 7C là 240 nên áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{b}{4} = \frac{a}{3} = \frac{c}{5} = \frac{{a + c}}{{3 + 5}} = \frac{{240}}{8} = 30\).
Từ đó suy ra:
\(\begin{array}{l}a = 30.3 = 90\\b = 30.4 = 120\\c = 30.5 = 150\end{array}\) (Thỏa mãn)
Vậy số vở lớp 7A, 7B, 7C thu được lần lượt là 90; 120; 150 cuốn.
Một đội công nhân có 15 người làm xong công việc trong 90 ngày. Hỏi cần bổ sung thêm bao nhiêu công nhân để hoàn thành công việc đó chỉ trong 50 ngày.
Áp dụng tính chất của hai đại lượng tỉ lệ nghịch với nhau.
Gọi số công nhân mà đội cần để hoàn thành công việc trong 50 ngày là x (người) (\(x \in N*,x > 15\))
Vì lượng công việc là không thay đổi nên số công nhân và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch.
Theo tính chất của hai đại lượng tỉ lệ nghịch, ta có:
\(15.90 = x.50\) suy ra \(x = \frac{{15.90}}{{50}} = 27\).
Vậy đội cần bổ sung thêm 27 – 15 = 12 công nhân để hoàn thành công việc trong 50 ngày.
So sánh các cạnh của tam giác ABC có \(\widehat A = {50^0},\,\widehat B = {60^0}\).
Áp dụng định lí tổng ba góc của một tam giác và quan hệ giữa góc và cạnh đối diện trong một tam giác.
Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^0}\\\widehat C = {180^0} - \widehat A - \widehat B\\ = {180^0} - {50^0} - {60^0}\\ = {70^0}\end{array}\)
Trong tam giác ABC, ta có:
\(\widehat C > \widehat B > \widehat A\left( {{{70}^0} > {{60}^0} > {{50}^0}} \right)\) suy ra \(AB > AC > BC\).
Cho tam giác ABC có AB = AC, N là trung điểm của BC.
a) Chứng minh \(\Delta ABN = \Delta ACN\).
b) Qua A kẻ đường thẳng a vuông góc với AN. Chứng minh a // BC.
c) Vẽ điểm F sao cho N là trung điểm của AF. Chứng minh AB + AC > 2AN.
a) Dựa vào các trường hợp bằng nhau của hai tam giác.
b) Chứng minh \(AN \bot BC\) suy ra a // BC.
c) Dựa vào bất đẳng thức tam giác để chứng minh.
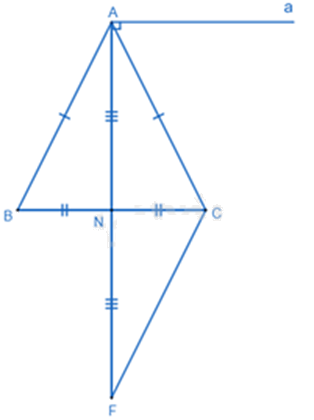
a) Xét \(\Delta ABN\) và \(\Delta ACN\) có:
\(\begin{array}{l}AB = AC(gt)\\BN = CN(gt)\\AN\,chung\end{array}\)
Suy ra \(\Delta ABN = \Delta ACN\)(c.c.c) (đpcm)
b) Ta có \(\Delta ABN = \Delta ACN\) suy ra \(\widehat {ANB} = \widehat {ANC}\).
Mà hai góc này là hai góc kề bù nên \(\widehat {ANB} = \widehat {ANC} = \frac{{{{180}^0}}}{2} = {90^0}\).
Do đó \(AN \bot BC\). Mà \(a \bot AN\) (gt)
Suy ra \(a//BC\) (từ vuông góc đến song song) (đpcm).
c) Xét \(\Delta ABN\) và \(\Delta FCN\) có:
\(\begin{array}{l}AN = NF(gt)\\BN = CN(gt)\end{array}\)
\(\widehat {ANB} = \widehat {FNC}\) (hai góc đối đỉnh)
Suy ra \(\Delta ABN = \Delta FCN\)(c.g.c) (đpcm)
Suy ra AB = CF.
Xét \(\Delta ACF\) có:
\(\begin{array}{l}CF + AC > AF\\AB + AC > 2AN\end{array}\)
(vì AB = CF và AF = 2AN) (đpcm).
Đề thi giữa kì 2 Toán 7 Kết nối tri thức - Đề số 7 là một bài kiểm tra quan trọng giúp học sinh đánh giá mức độ nắm vững kiến thức đã học trong nửa học kì. Đề thi bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính như biểu thức đại số, phương trình bậc nhất một ẩn, bất đẳng thức, tam giác, và các yếu tố liên quan đến hình học.
Thông thường, đề thi giữa kì 2 Toán 7 Kết nối tri thức - Đề số 7 sẽ có cấu trúc gồm:
Để giải tốt đề thi giữa kì 2 Toán 7 Kết nối tri thức - Đề số 7, học sinh cần:
Bài toán: Giải phương trình 2x + 5 = 11
Lời giải:
Để chuẩn bị tốt nhất cho kỳ thi giữa kì 2 Toán 7 Kết nối tri thức, học sinh có thể tham khảo các tài liệu sau:
Hãy dành thời gian ôn tập kiến thức một cách nghiêm túc và có kế hoạch. Đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè nếu gặp khó khăn trong quá trình học tập. Chúc các em học sinh đạt kết quả tốt nhất trong kỳ thi giữa kì 2 Toán 7 Kết nối tri thức!
| Dạng bài tập | Ví dụ |
|---|---|
| Thu gọn biểu thức | 3x + 2y - x + 5y |
| Giải phương trình | 5x - 10 = 0 |
| Tính góc trong tam giác | Tam giác ABC có góc A = 60 độ, góc B = 80 độ. Tính góc C. |