Chào mừng các em học sinh lớp 7 đến với đề thi học kì 1 môn Toán - Đề số 15, chương trình Kết nối tri thức.
Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong học kì 1.
Giaitoan.edu.vn cung cấp đề thi và đáp án chi tiết, giúp các em tự học hiệu quả và đạt kết quả tốt nhất.
Căn bậc hai số học của 16 là
Số nào là số vô tỉ trong các số sau:
Trong các số sau \( - 1\frac{2}{3};\,\,\,\frac{{ - 3}}{{ - 13}};\,\,\,\frac{0}{7};\,\,\,\frac{{ - 5}}{9};\,\,\,\frac{8}{{17}};\,\,0,23\) có bao nhiêu số hữu tỉ dương?
Kết quả của phép tính \(\sqrt {81} - 2\sqrt {16} \) là:
Cho \(\left| x \right|\) = 25 thì giá trị của x là:
Kết quả làm tròn số 17,8569 đến hàng phần trăm là:
Cho điểm \(C\) thuộc trung trực của đoạn thẳng \(AB\). Biết \(AC = 10\,{\rm{cm}}\). Độ dài đoạn thẳng \(CB\) là
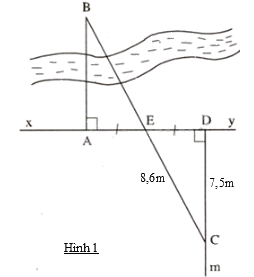
Trênhình 1, khoảng cách giữa hai địa điểm \(A\) và \(B\) là bao nhiêu ?
Một tam giác cân có số đo góc ở đáy gấp hai lần số đo góc ở đỉnh. Số đo góc ở đỉnh của tam giác cân đó là:
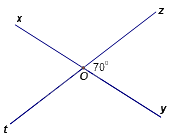
Trong hình vẽ dưới đây, góc xOt có số đo bằng:
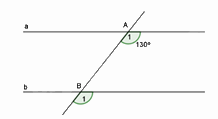
Cho hình vẽ bên, biết a// b. Số đo \({\hat B_1}\) là:
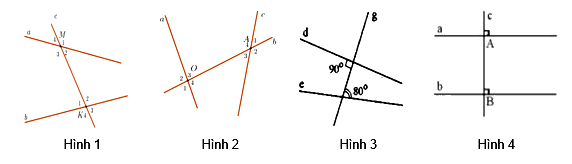
Hình vẽ nào sau đây có hai đường thẳng song song?
Thực hiện phép tính (Tính hợp lý nếu có thể):
a) \(\frac{5}{3} + \frac{{ - 7}}{{12}} + {\left( { - \frac{1}{2}} \right)^2}\)
b) \(\frac{{ - 17}}{{25}}.\frac{3}{{10}} + \frac{{ - 33}}{{25}}.\frac{3}{{10}} + \frac{3}{{10}}\)
Tìm số hữu tỉ x biết:\(\left| {0,5x + \frac{3}{2}} \right| = \frac{3}{4}\)
Tại cửa hàng bán hoa, giá bán ban đầu của một bó hoa là 80 000 đồng. Vào ngày Quốc tế phụ nữ 8/3, cửa hàng đã quyết định giảm giá 20% cho mỗi bó hoa so với giá bán ban đầu và nếu khách hàng mua 10 bó trở lên thì từ bó thứ 10 trở đi, mỗi bó hoa khách hàng sẽ chỉ phải trả với giá bằng 75% của giá đã giảm trước đó. Một công ty muốn đặt 50 bó hoa để tặng cho các nhân viên nữ. Tính tổng số tiền công ty phải trả.
Cho biểu đồ sau:
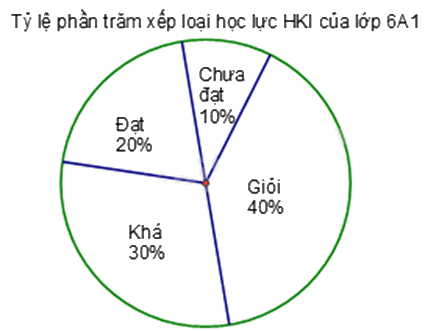
a) Biểu đồ biểu diễn thông tin về vấn đề gì? Tỉ lệ % của mỗi đối tượng so với toàn thể là bao nhiêu?
b) Tính tổng số học sinh giỏi và khá của lớp 6A1 biết lớp có 50 học sinh.
Cho \(\Delta ABC\) có \(AB < BC\). Trên tia BA lấy điểm D sao cho \(BC = BD\). Tia phân giác \(\widehat B\) cắt AC ở E. Gọi K là trung điểm của DC.
a) Chứng minh \(\Delta BED = \Delta BEC\).
b) Chứng minh \(EK \bot DC\).
c) Chứng minh B, K, E thẳng hàng.
d) Kẻ \(AH \bot DC,\left( {H \in DC} \right)\). \(\Delta ABC\) cần thêm điều kiện gì để \(\widehat {DAH} = {45^0}\).
Căn bậc hai số học của 16 là
Đáp án : B
Sử dụng kiến thức về căn bậc hai số học: Căn bậc hai số học của số a không âm là số x không âm sao cho \({x^2} = a\).
Căn bậc hai số học của 16 là \(\sqrt {16} = 4\).
Số nào là số vô tỉ trong các số sau:
Đáp án : A
Số vô tỉ được biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn.
Ta có:
\(\sqrt {25} = 5\) là số hữu tỉ.
– 5,(4561) là số thập phân vô hạn tuần hoàn.
\(\frac{5}{3}\) là số hữu tỉ.
Vậy chỉ có \(\sqrt 5 \) là số vô tỉ.
Trong các số sau \( - 1\frac{2}{3};\,\,\,\frac{{ - 3}}{{ - 13}};\,\,\,\frac{0}{7};\,\,\,\frac{{ - 5}}{9};\,\,\,\frac{8}{{17}};\,\,0,23\) có bao nhiêu số hữu tỉ dương?
Đáp án : C
Số hữu tỉ dương là các số lớn hơn 0 có thể viết dưới dạng phân số.
Ta có: \( - 1\frac{2}{3} < 0\); \(\frac{{ - 3}}{{ - 13}} = \frac{3}{{13}} > 0\); \(\frac{0}{7} = 0\); \(\frac{{ - 5}}{9} < 0\); \(\frac{8}{{17}} > 0\); \(0,23 = \frac{{23}}{{100}} > 0\).
Vậy có 3 số hữu tỉ dương: \(\frac{{ - 3}}{{ - 13}};\frac{8}{{17}};0,23\).
Kết quả của phép tính \(\sqrt {81} - 2\sqrt {16} \) là:
Đáp án : A
Sử dụng kiến thức về căn bậc hai số học: Căn bậc hai số học của số a không âm là số x không âm sao cho \({x^2} = a\).
\(\sqrt {81} - 2\sqrt {16} = 9 - 2.4 = 9 - 8 = 1\).
Cho \(\left| x \right|\) = 25 thì giá trị của x là:
Đáp án : D
Sử dụng định nghĩa giá trị tuyệt đối của một số:
\(\left| x \right| = \left\{ \begin{array}{l}x\,khi\,x \ge 0\\ - x\,khi\,x < 0\end{array} \right.\).
\(\left| x \right|\) = 25 thì x = 25 hoặc x = – 25.
Kết quả làm tròn số 17,8569 đến hàng phần trăm là:
Đáp án : C
Dựa vào cách làm tròn số với độ chính xác cho trước.
Do 6 > 5 \( \Rightarrow \) Làm tròn 17,8569 đến hàng phần trăm là : 17,8569 ≈ 17,86.
Vậy làm tròn 17,8569 đến hàng phần trăm là 17,86.
Cho điểm \(C\) thuộc trung trực của đoạn thẳng \(AB\). Biết \(AC = 10\,{\rm{cm}}\). Độ dài đoạn thẳng \(CB\) là
Đáp án : A
Dựa vào tính chất đường trung trực của đoạn thẳng.
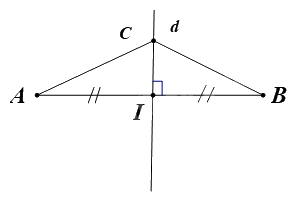
Điểm \(C\) thuộc trung trực của đoạn thẳng \(AB\) nên \(CB = AC = 10\,{\rm{cm}}\) (tính chất đường trung trực của một đoạn thẳng).
Trênhình 1, khoảng cách giữa hai địa điểm \(A\) và \(B\) là bao nhiêu ?
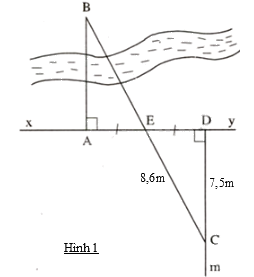
Đáp án : A
Chứng minh \(\Delta ABE = \Delta DCE\) suy ra cạnh tương ứng bằng nhau.
Xét tam giác ABE và tam giác DCE có :
\(\widehat A = \widehat D = {90^0}\)
\(AE = ED\)
\(\widehat {AEB} = \widehat {DEC}\) (hai góc đối đỉnh)
\( \Rightarrow \Delta ABE = \Delta DCE\) (g.c.g) . Suy ra \(AB = CD = 7,5\)cm.
Một tam giác cân có số đo góc ở đáy gấp hai lần số đo góc ở đỉnh. Số đo góc ở đỉnh của tam giác cân đó là:
Đáp án : B
Dựa vào đặc điểm của tam giác cân.
Gọi số đo góc ở đỉnh là x, thì số đo góc ở đáy là 2x.
Vì tam giác này là tam giác cân nên 2 góc ở đáy bằng nhau. Mà tổng ba góc trong một tam giác bằng 1800 nên x + 2x + 2x = 5x = 1800 \( \Rightarrow \) x = 360.
Trong hình vẽ dưới đây, góc xOt có số đo bằng:
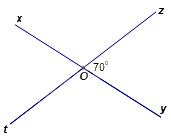
Đáp án : B
Dựa vào tính chất hai góc đối đỉnh.
Ta có góc yOz và góc xOt là hai góc đối đỉnh nên \(\widehat {xOt} = \widehat {yOz} = {70^0}\).
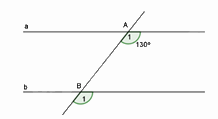
Cho hình vẽ bên, biết a// b. Số đo \({\hat B_1}\) là:
Đáp án : C
Dựa vào tính chất của hai đường thẳng song song.
Vì a // b nên \(\widehat {{A_1}} = \widehat {{B_1}} = {130^0}\) (hai góc đồng vị).
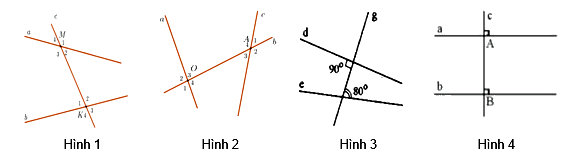
Hình vẽ nào sau đây có hai đường thẳng song song?
Đáp án : D
Dựa vào dấu hiệu nhận biết hai đường thẳng song song.
Hình 1 không có cặp góc nào bằng nhau nên không có hai đường thẳng song song.
Hình 2 không có cặp góc nào bằng nhau nên không có hai đường thẳng song song.
Hình 3 không có cặp góc nào bằng nhau nên không có hai đường thẳng song song.
Hình 4 có cặp góc đồng vị bằng nhau (= 900) nên có hai đường thẳng song song.
Thực hiện phép tính (Tính hợp lý nếu có thể):
a) \(\frac{5}{3} + \frac{{ - 7}}{{12}} + {\left( { - \frac{1}{2}} \right)^2}\)
b) \(\frac{{ - 17}}{{25}}.\frac{3}{{10}} + \frac{{ - 33}}{{25}}.\frac{3}{{10}} + \frac{3}{{10}}\)
a) Dựa vào thứ tự thực hiện để tính.
b) Nhóm nhân tử chung để tính.
a) \(\frac{5}{3} + \frac{{ - 7}}{{12}} + {\left( { - \frac{1}{2}} \right)^2}\)\( = \frac{5}{3} + \frac{{ - 7}}{{12}} + \frac{1}{4}\)\( = \frac{{13}}{{12}} + \frac{1}{4}\)\( = \frac{4}{3}\)
b) \(\frac{{ - 17}}{{25}}.\frac{3}{{10}} + \frac{{ - 33}}{{25}}.\frac{3}{{10}} + \frac{3}{{10}}\)\( = \frac{3}{{10}}\left( {\frac{{ - 17}}{{25}} + \frac{{ - 33}}{{25}} + 1} \right)\)\( = \frac{3}{{10}}\left( { - 2 + 1} \right) = \frac{{ - 3}}{{10}}\)
Tìm số hữu tỉ x biết:\(\left| {0,5x + \frac{3}{2}} \right| = \frac{3}{4}\)
\(\left| x \right| = a\) khi và chỉ khi x = a hoặc x = -a.
\(\left| {0,5x + \frac{3}{2}} \right| = \frac{3}{4}\)
Suy ra \(0,5x + \frac{3}{2} = \frac{3}{4}\) hoặc \(0,5x + \frac{3}{2} = \frac{{ - 3}}{4}\)
TH1. \(0,5x + \frac{3}{2} = \frac{3}{4}\)
\(0,5x = \frac{3}{4} - \frac{3}{2}\)
\(0,5x = \frac{{ - 3}}{4}\)
\(x = \frac{{ - 3}}{2}\)
TH2. \(0,5x + \frac{3}{2} = \frac{{ - 3}}{4}\)
\(0,5x = \frac{{ - 3}}{4} - \frac{3}{2}\)
\(0,5x = \frac{{ - 9}}{4}\)
\(x = \frac{{ - 9}}{2}\)
Vậy \(x \in \left\{ {\frac{{ - 3}}{2};\frac{{ - 9}}{2}} \right\}\).
Tại cửa hàng bán hoa, giá bán ban đầu của một bó hoa là 80 000 đồng. Vào ngày Quốc tế phụ nữ 8/3, cửa hàng đã quyết định giảm giá 20% cho mỗi bó hoa so với giá bán ban đầu và nếu khách hàng mua 10 bó trở lên thì từ bó thứ 10 trở đi, mỗi bó hoa khách hàng sẽ chỉ phải trả với giá bằng 75% của giá đã giảm trước đó. Một công ty muốn đặt 50 bó hoa để tặng cho các nhân viên nữ. Tính tổng số tiền công ty phải trả.
Tính giá bó hoa sau khi giảm 20%.
Tính giá bó hoa khi mua từ bó thứ 10 trở đi.
Tính tổng số tiền công ty phải trả khi mua 50 bó hoa = 9.giá bó hoa sau khi giảm 20% + 41.giá bó hoa khi mua từ bó thứ 10 trở đi.
Sau khi giảm 20% thì giá 1 bó hoa bằng 100% - 20% = 80% giá bó hoa ban đầu.
Giá 1 bó hoa sau khi giảm 20% là: 80 000.80% = 64000 đồng
Giá 1 bó hoa từ bó thứ 10 trở đi: 64 000.75% = 48000 đồng
Vậy tổng số tiền công ty phải trả khi mua 50 bó hoa:
64 000.9 + 48000.41 = 2 544 000 đồng
Cho biểu đồ sau:
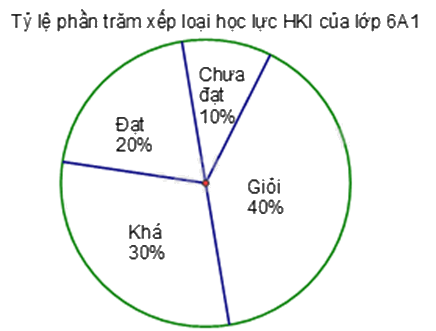
a) Biểu đồ biểu diễn thông tin về vấn đề gì? Tỉ lệ % của mỗi đối tượng so với toàn thể là bao nhiêu?
b) Tính tổng số học sinh giỏi và khá của lớp 6A1 biết lớp có 50 học sinh.
a) Xác định biểu đồ biểu diễn thông tin gì. Dựa vào biểu đồ để xác định số phần trăm mỗi đối tượng.
b) Lấy tổng số học sinh nhân với số phần trăm học sinh giỏi và khá.
a) Biểu đồ biểu diễn "Tỉ lệ phần trăm xếp loại học lực HKI của lớp 6A1".
Bảng biểu diễn tỉ lệ % của mỗi đối tượng :

(Có thể lựa chọn vẽ bảng hoặc liệt kê phần trăm)
b) Tổng số phần trăm học sinh giỏi và khá là : 40% + 30% = 70%.
Số học sinh giỏi và khá của lớp 6A1 là : 50.70% = 35 (học sinh).
Cho \(\Delta ABC\) có \(AB < BC\). Trên tia BA lấy điểm D sao cho \(BC = BD\). Tia phân giác \(\widehat B\) cắt AC ở E. Gọi K là trung điểm của DC.
a) Chứng minh \(\Delta BED = \Delta BEC\).
b) Chứng minh \(EK \bot DC\).
c) Chứng minh B, K, E thẳng hàng.
d) Kẻ \(AH \bot DC,\left( {H \in DC} \right)\). \(\Delta ABC\) cần thêm điều kiện gì để \(\widehat {DAH} = {45^0}\).
a) Chứng minh \(\Delta BED = \Delta BEC\) theo trường hợp cạnh – góc – cạnh.
b) Chứng minh \(\Delta EKD = \Delta EKC\) \( \Rightarrow \widehat {{K_1}} = \widehat {{K_2}} = {90^0}\)
c) Chứng minh \(BK \bot DC\) và \(EK \bot DC\) nên B, K, E thẳng hàng.
d) Sử dụng tính chất hai đường thẳng song song.
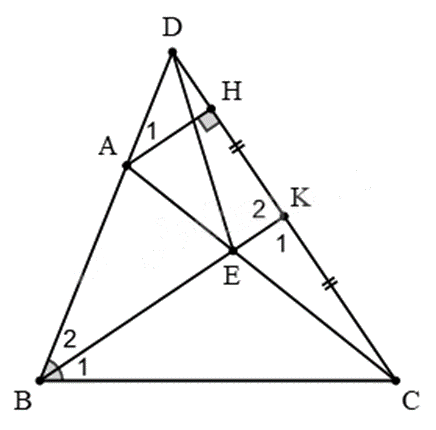
a) Xét \(\Delta BED\) và \(\Delta BEC\) có:
BD = BC (gt)
\(\widehat {{B_2}} = \widehat {{B_1}}\) (BE là tia phân giác của \(\widehat {ABC}\))
BE chung
\( \Rightarrow \Delta BED = \Delta BEC\)(c.g.c) (đpcm)
\( \Rightarrow DE = EC\) (hai cạnh tương ứng)
b) Xét \(\Delta EKD\) và \(\Delta EKC\) có:
ED = EC (cmt)
EK chung
DK = KC (K là trung điểm của DC)
\( \Rightarrow \Delta EKD = \Delta EKC\)(c.c.c)
\( \Rightarrow \widehat {{K_1}} = \widehat {{K_2}}\)(hai cặp góc tương ứng)
Mà \(\widehat {{K_1}}\) và \(\widehat {{K_2}}\) là hai góc kề bù nên \(\widehat {{K_1}} = \widehat {{K_2}} = \frac{{{{180}^0}}}{2} = {90^0}\) hay \(EK \bot DC\). (1) (đpcm)
c) Xét \(\Delta BKD\) và \(\Delta BKC\) có:
BD = BC (gt)
BK chung
DK = KC (K là trung điểm của DC)
\( \Rightarrow \Delta BKD = \Delta BKC\)(c.c.c)
\( \Rightarrow \widehat {BKD} = \widehat {BKC}\)(hai cặp góc tương ứng)
Mà \(\widehat {BKD}\) và \(\widehat {BKC}\) là hai góc kề bù nên \(\widehat {BKD} = \widehat {BKC} = \frac{{{{180}^0}}}{2} = {90^0}\) hay \(BK \bot DC\) (2)
Từ (1) và (2) suy ra B, E, K thẳng hàng. (đpcm)
d) Ta có: \(AH \bot DC\); \(BK \bot DC \Rightarrow AH//BK\)
\( \Rightarrow \widehat {{A_1}} = \widehat {{B_2}}\) (hai góc đồng vị).
Để \(\widehat {{A_1}} = {45^0}\) thì \(\widehat {{B_2}} = {45^0}\), mà \(\widehat {{B_2}} = \widehat {{B_1}} = \frac{1}{2}\widehat {ABC}\) nên \(\widehat {ABC} = {45^0}.2 = {90^0}\) hay tam giác ABC vuông tại B.
Vậy tam giác ABC tam giác cân tại B thì ta có \(\widehat {DAH} = {45^0}\).
Đề thi học kì 1 Toán 7 - Đề số 15 chương trình Kết nối tri thức là một bài kiểm tra quan trọng giúp học sinh đánh giá mức độ nắm vững kiến thức đã học trong nửa học kì đầu tiên. Đề thi bao gồm các dạng bài tập khác nhau, từ trắc nghiệm đến tự luận, tập trung vào các chủ đề chính như số hữu tỉ, số thực, biểu thức đại số, phương trình bậc nhất một ẩn, bất đẳng thức và các ứng dụng thực tế của Toán học.
Thông thường, đề thi học kì 1 Toán 7 - Đề số 15 - Kết nối tri thức sẽ được chia thành các phần sau:
Các bài tập về số hữu tỉ và số thực thường yêu cầu học sinh:
Các bài tập về biểu thức đại số thường yêu cầu học sinh:
Các bài tập về phương trình bậc nhất một ẩn thường yêu cầu học sinh:
Các bài tập về bất đẳng thức thường yêu cầu học sinh:
Bài 1: Giải phương trình 2x + 5 = 11
Giải:
Kết luận: Phương trình có nghiệm x = 3
Bài 2: Tìm giá trị của biểu thức A = 3x2 - 2x + 1 khi x = -1
Giải:
Thay x = -1 vào biểu thức A, ta được:
A = 3(-1)2 - 2(-1) + 1 = 3(1) + 2 + 1 = 3 + 2 + 1 = 6
Kết luận: Giá trị của biểu thức A khi x = -1 là 6
Giaitoan.edu.vn luôn đồng hành cùng các em học sinh trong quá trình học tập. Chúng tôi cung cấp đầy đủ các tài liệu học tập, đề thi, đáp án và các bài giảng online chất lượng cao. Hãy truy cập giaitoan.edu.vn để được hỗ trợ tốt nhất!