Chào mừng các em học sinh lớp 7 đến với đề thi học kì 1 môn Toán - Đề số 7, chương trình Kết nối tri thức.
Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong học kì 1.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
I. TRẮC NGHIỆM ( 3 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Số đối của \(\dfrac{{ - 7}}{{12}}\) là:
A. \(\dfrac{7}{{12}}\)
B. \(\dfrac{7}{{ - 12}}\)
C. \(\dfrac{{12}}{{ - 7}}\)
D. \(\dfrac{{12}}{7}\)
Câu 2: Chọn khẳng định đúng.
A. \(\dfrac{{ - 37}}{{41}} > \dfrac{{23}}{{ - 17}}\)
B. \({\left( {\dfrac{1}{3}} \right)^{12}} > {\left( {\dfrac{1}{3}} \right)^{10}}\)
C. \({\left( {2,5} \right)^6} = {\left( {0,5} \right)^{12}}\)
D. \({\left( {2,5} \right)^4} < {\left( { - 2,5} \right)^5}\)
Câu 3: Chọn đáp án sai. Nếu \(\sqrt x = \dfrac{2}{3}\) thì:
A. \(x = {\left( { - \dfrac{2}{3}} \right)^2}\)
B. \(x = - {\left( { - \dfrac{2}{3}} \right)^2}\)
C. \(x = \dfrac{4}{9}\)
D. \(x = {\left( {\dfrac{2}{3}} \right)^2}\)
Câu 4: Trong các phát biểu sau, phát biểu nào sai?
A. Giá trị tuyệt đối của một số thực là một số dương hoặc bằng 0.
B. Hai số có giá trị tuyệt đối bằng nhau là hai số bằng nhau hoặc đối nhau.
C. Hai số đối nhau có giá trị tuyệt đối bằng nhau.
D. Giá trị tuyệt đối của một số thực luôn bằng chính nó.
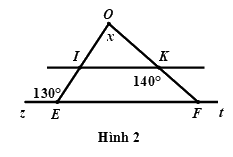
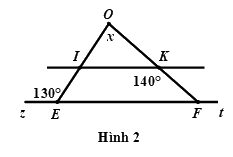
Câu 5: Quan sát Hình 2, có \(IK//EF\). Hãy tính giá trị của \(x\)?
A. \(x = {70^0}\)
B. \(x = {110^0}\)
C. \(x = {120^0}\)
D. \(x = {90^0}\)
Câu 6:
Cho tam giác \(ABC\) có \(AB < AC\). Tia phân giác của góc \(A\) cắt \(BC\) ở \(K\). Từ \(B\) kẻ đường vuông góc với \(AK\) tại \(H\) cắt \(AC\) ở \(D\). Chọn câu sai.
A. \(HB = AD\)
B. \(HB = HD\)
C. \(AB = AD\)
D. \(\widehat {ABH} = \widehat {ADH}\)
Câu 7: Số học sinh đăng ký học bổ trợ các Câu lạc bộ Toán, Ngữ văn, Tiếng anh của lớp 7 của một trường được biểu diễn qua biểu đồ hình quạt tròn như sau:
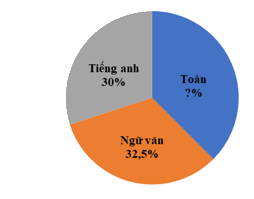
Tính số phần trăm học sinh đăng ký môn Toán là bao nhiêu?
A. 40%
B. 37,5%
C. 30%
D. 35%
Câu 8: Cho biểu đồ biểu diễn chiều cao trung bình của nam và nữ ở một số quốc gia châu Á:
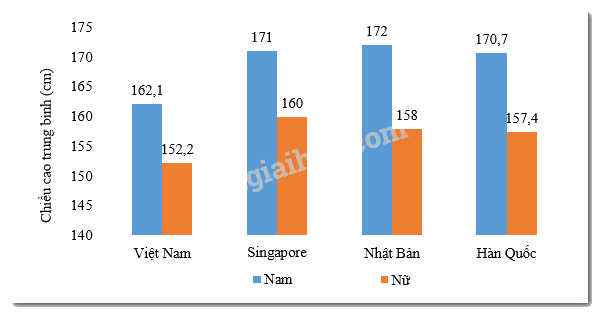
Sự chênh lệch chiều cao giữa nam và nữ của nước nào là lớn nhất?
A. Việt Nam
B. Singapore
C. Nhật Bản
D. Hàn Quốc
Câu 9: Phát biểu định lí sau bằng lời:
GT | \(a//b,c \bot a\) |
KL | \(c \bot b\) |
A. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
B. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó song song với đường thẳng kia.
C. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó tạo với đường thẳng kia một góc \({60^0}\).
D. Cả A, B, C đều đúng.
Câu 10: Vẽ \(\angle xOy = {50^0}\). Vẽ tia \(Om\) là tia phân giác của góc \(xOy\). Vẽ tia \(On\) là tia đối của tia \(Ox\). Tính góc \(mOn\).
A. \(\angle mOn = {125^0}\)
B. \(\angle mOn = {155^0}\)
C. \(\angle mOn = {160^0}\)
D. \(\angle mOn = {175^0}\)
Phần II. Tự luận (7 điểm):
Bài 1: (2,0 điểm)
Thực hiện phép tính:
a) \(\dfrac{7}{2}.\dfrac{{11}}{6} - \dfrac{7}{2}.\dfrac{5}{6}\)
b) \(\sqrt {36} - 3.\sqrt {\dfrac{1}{4}} + \left| {\dfrac{{ - 3}}{2}} \right|\)
c) \({\left( {\dfrac{{ - 1}}{2}} \right)^3} - \dfrac{7}{8}:\dfrac{7}{4} + \left| {\dfrac{{ - 9}}{8}} \right| + \sqrt {81} \)
Bài 2 (2,0 điểm).Tìm \(x\):
a) \(\dfrac{3}{5}x - \dfrac{6}{7} = \dfrac{1}{7}\)
b) \({\left( {2x - 1} \right)^3} = 64\)
c) \(2\left| {x + 1} \right| - 0,5 = \sqrt {\dfrac{1}{9}} \)
Bài 3: (3,5 điểm)
Cho góc nhọn \(xOy\), lấy điểm \(A\) trên tia \(Ox\) (điểm\(A\) khác \(O\)) và điểm \(B\) trên tia \(Oy\) sao cho \(OA = OB\). Gọi \(M\) là trung điểm của \(AB\).
a) Chứng minh: \(\Delta OAM = \Delta OBM\)
b) Trên tia \(OM\) lấy điểm \(H\) sao cho \(OM < OH\). Chứng minh \(HA = HB\).
c) Qua \(H\) kẻ đường thẳng song song với \(AB\) cắt \(Ox\) tại \(E\) cắt \(Oy\) tại \(K\). Chứng minh \(OH\) là đương trung trực của \(EK\).
d) Gọi giao điểm của \(AK\) và \(BE\) là \(N\). Chứng minh ba điểm \(O,M,N\) thẳng hàng.
Bài 4: (0,5 điểm)
Tìm giá trị nhỏ nhất của biểu thức \(A = {x^2} + 3\sqrt x - 2024\) với \(x \ge 0\).
Phần I: Trắc nghiệm:
1.A | 2.A | 3.B | 4.D | 5.D | 6.A | 7.B | 8.C | 9. A | 10.B |
Câu 1
Phương pháp:
Số đối của số hữu tỉ \(a\) kí hiệu là \( - a\).
Cách giải:
Số đối của \(\dfrac{{ - 7}}{{12}}\) là: \( - \left( {\dfrac{{ - 7}}{{12}}} \right) = \dfrac{7}{{12}}\)
Chọn A.
Câu 2
Phương pháp:
Sử dụng phương pháp so sánh trung gian.
Cách giải:
+ Ta có: \(37 < 41\) nên \(\dfrac{{37}}{{41}} < 1\) suy ra \(\dfrac{{ - 37}}{{41}} > - 1\) (1)
\(23 > 17\) nên \(\dfrac{{23}}{{17}} > 1\) suy ra \(\dfrac{{23}}{{ - 17}} < - 1\) (2)
Từ (1) và (2), suy ra \(\dfrac{{23}}{{ - 17}} < - 1 < \dfrac{{ - 37}}{{41}}\), do đó, \(\dfrac{{ - 37}}{{41}} > \dfrac{{23}}{{ - 17}}\)
Vậy đáp án A đúng.
Chọn A.
Câu 3
Phương pháp:
Căn bậc hai số học của số \(a\) không âm là số \(x\) không âm sao cho \({x^2} = a\).
Sử dụng tính chất: \({x^2} = {\left( { - x} \right)^2}\)
Cách giải:
\(\sqrt {{{\left( { - \dfrac{2}{3}} \right)}^2}} = \sqrt {{{\left( {\dfrac{2}{3}} \right)}^2}} = \sqrt {\dfrac{4}{9}} = \dfrac{2}{3}\) nên đáp án A,C,D đúng
Do chỉ tồn tại căn bậc hai số học của một số không âm nên đáp án B sai.
Chọn B.
Câu 4
Phương pháp:
Vận dụng kiến thức giá trị tuyệt đối của một số thực, tìm phát biểu sai.
Cách giải:
Phát biểu A đúng vì giá trị tuyệt đối của một số thực là một số không âm.
Phát biểu B đúng vì hai số có giá trị tuyệt đối bằng nhau là hai số bằng nhau hoặc đối nhau.
Phát biểu C đúng vì hai số đối nhau có điểm biểu diễn cách đều điểm gốc 0 nên giá trị tuyệt đối của chúng bằng nhau.
Phát biểu D sai vì giá trị tuyệt đối của số âm là số đối của nó.
Chọn D.
Câu 5
Phương pháp:
Hai góc kề bù có tổng số đo bằng \({180^0}\)
Hai đường thẳng song song thì hai góc ở vị trí đồng vị bằng nhau.
Vận dụng định lý: Tổng ba góc trong một tam giác bằng \({180^0}\).
Cách giải:
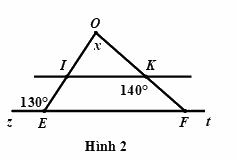
* Ta có: \(\angle zEO + \angle OEF = {180^0}\) (hai góc kề bù)
\(\begin{array}{l} \Rightarrow {130^0} + \angle OEF = {180^0}\\ \Rightarrow \angle OEF = {180^0} - {130^0}\\ \Rightarrow \angle OEF = {50^0}\end{array}\)
* \(IK//EF\) (giá thiết) \( \Rightarrow \angle OEF = \angle OIK\) (hai góc đồng vị) do đó, \(\angle OIK = {50^0}\)
* Ta có: \(\angle IKO + \angle IKF = {180^0}\) (hai góc kề bù)
\(\begin{array}{l} \Rightarrow \angle IKO + {140^0} = {180^0}\\ \Rightarrow \angle IKO = {180^0} - {140^0}\\ \Rightarrow \angle IKO = {40^0}\end{array}\)
* Xét \(\Delta OIK\) có: \(\angle O + \angle OIK + \angle OKI = {180^0}\) (định lí tổng ba góc trong một tam giác)
\(\begin{array}{l} \Rightarrow x + {50^0} + {40^0} = {180^0}\\ \Rightarrow x + {90^0} = {180^0}\\ \Rightarrow x = {180^0} - {90^0}\\ \Rightarrow x = {90^0}\end{array}\)
Vậy \(x = {90^0}\)
Chọn D.
Câu 6
Phương pháp:
+ Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
+ Hai tam giác bằng nhau có các cặp cạnh, cặp góc tương ứng bằng nhau
Cách giải:
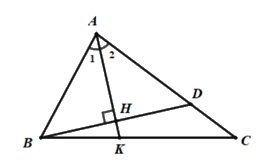
Vì \(AK\) là tia phân giác của \(\angle BAC\) nên \(\angle {A_1} = \angle {A_2}\)
Theo giả thiết ta có: \(BH \bot AK \Rightarrow \angle AHB = \angle AHD = 90^\circ \)
Xét tam giác \(AHB\) và tam giác \(AHD\) có:
\(\angle {A_1} = \angle {A_2}\)
\(AH\) là cạnh chung
\(\angle AHB = \angle AHD = 90^\circ \)
Nên \(\Delta AHB = \Delta AHD\) (g.c.g)
Suy ra: \(HB = HD\) (hai cạnh tương ứng) nên B đúng
\(AB = AD\) (hai cạnh tương ứng) nên C đúng
\(\angle ABH = \angle ADH\) (hai góc tương ứng) nên D đúng
Chọn A.
Câu 7
Phương pháp:
Đọc và phân tích dữ liệu của biểu đồ hình quạt tròn.
Cách giải:
Số phần trăm học sinh đăng ký môn Toán là: \(100\% - 32,5\% - 30\% = 37,5\% \)
Chọn B.
Câu 8
Phương pháp:
Sử dụng biểu đồ cột kép, quan sát và trả lời câu hỏi.
Cách giải:
*) Chiều cao trung bình của nam:
Việt Nam: \(162,1cm\)
Singapore: \(171cm\)
Nhật Bản: \(172cm\)
Hàn Quốc: \(170,7cm\)
*) Chiều cao trung bình của nữ:
Việt Nam: \(152,2cm\)
Singapore:\(160cm\)
Nhật Bản: \(158cm\)
Hàn Quốc: \(157,4cm\)
Sự chênh lệch chiều cao giữa nam và nữ ở Việt Nam là:
\(162,1 - 152,2 = 9,9\,\,\left( {cm} \right)\)
Sự chênh lệch chiều cao giữa nam và nữ ở Singapore là:
\(171 - 160 = 11\,\,\left( {cm} \right)\)
Sự chênh lệch chiều cao giữa nam và nữ ở Nhật Bản là:
\(172 - 158 = 14\,\,\left( {cm} \right)\)
Sự chênh lệch chiều cao giữa nam và nữ ở Hàn Quốc là:
\(170,7 - 157,4 = 13,3\,\,\left( {cm} \right)\)
Sự chênh lệch chiều cao giữa nam và nữ ở Nhật Bản là lớn nhất.
Chọn C.
Câu 9
Phương pháp:
Định lí là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … thì ….
Cách giải:
Phát biểu định lí: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
Chọn A.
Câu 10
Phương pháp
\(Oz\) là tia phân giác của \(\angle xOy\) thì ta có: \(\angle xOz = \angle zOy = \dfrac{{\angle xOy}}{2}\)
\(\angle xOz\) và \(\angle zOy\) là hai góc kề nhau thì ta có: \(\angle xOz + \angle zOy = \angle xOy\).
\(\angle xOz\) và \(\angle zOy\) là hai góc kề bù thì ta có: \(\angle xOy = \angle xOz + \angle zOy = {180^0}\)
Cách giải:
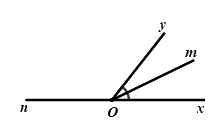
Vì \(Om\) là tia phân giác của \(\angle xOy\) nên \(\angle mOy = \dfrac{{\angle xOy}}{2} = \dfrac{{{{50}^0}}}{2} = {25^0}\)
Ta có: \(\angle nOy\) và \(\angle yOx\) là hai góc kề bù nên \(\angle nOy + \angle yOx = {180^0}\)
\(\begin{array}{l} \Rightarrow \angle nOy + {50^0} = {180^0}\\ \Rightarrow \angle nOy = {180^0} - {50^0} = {130^0}\end{array}\)
Ta có: \(\angle nOy\) và \(\angle yOm\) là hai góc kề nhau nên \(\angle nOy + \angle yOm = \angle nOm\)
\( \Rightarrow {130^0} + {25^0} = {155^0} = \angle nOm\)
Vậy \(\angle mOn = {155^0}\)
Chọn B.
Phần II. Tự luận (7 điểm):
Bài 1
Phương pháp:
Thực hiện phép tính với số hữu tỉ, giá trị tuyệt đối của một số hữu tỉ.
Cách giải:
a) \(\dfrac{7}{2}.\dfrac{{11}}{6} - \dfrac{7}{2}.\dfrac{5}{6}\) \(\begin{array}{l} = \dfrac{7}{2}.\left( {\dfrac{{11}}{6} + \dfrac{5}{6}} \right)\\ = \dfrac{7}{2}.\dfrac{{16}}{6}\\ = \dfrac{{28}}{3}\end{array}\) | b) \(\sqrt {36} - 3.\sqrt {\dfrac{1}{4}} + \left| {\dfrac{{ - 3}}{2}} \right|\) \(\begin{array}{l} = 6 - 3.\dfrac{1}{2} + \dfrac{3}{2}\\ = 6 + \left( {\dfrac{3}{2} - \dfrac{3}{2}} \right)\\ = 6 + 0 = 6\end{array}\) | c) \({\left( {\dfrac{{ - 1}}{2}} \right)^3} - \dfrac{7}{8}:\dfrac{7}{4} + \left| {\dfrac{{ - 9}}{8}} \right| + \sqrt {81} \) \(\begin{array}{l} = \dfrac{{ - 1}}{8} - \dfrac{7}{8}.\dfrac{4}{7} + \dfrac{9}{8} + 9\\ = \left( { - \dfrac{1}{8} + \dfrac{9}{8}} \right) - \dfrac{1}{2} + 9\\ = 1 - \dfrac{1}{2} + 9\\ = \dfrac{1}{2} + 9 = \dfrac{{19}}{2}\end{array}\) |
Bài 2
Phương pháp:
Thực hiện phép tính với số hữu tỉ, giá trị tuyệt đối của một số hữu tỉ.
Cách giải:
a) \(\dfrac{3}{5}x - \dfrac{6}{7} = \dfrac{1}{7}\) \(\begin{array}{l}\dfrac{3}{5}x = \dfrac{1}{7} + \dfrac{6}{7}\\\dfrac{3}{5}x = \dfrac{7}{7} = 1\\x = 1:\dfrac{3}{5}\\x = \dfrac{5}{3}\end{array}\) Vậy \(x = \dfrac{5}{3}\) | b) \({\left( {2x - 1} \right)^3} = 64\) \(\begin{array}{l}{\left( {2x - 1} \right)^3} = {4^3}\\2x - 1 = 4\\2x = 4 + 1\\2x = 5\\x = \dfrac{5}{2}\end{array}\) Vậy \(x = \dfrac{5}{2}\) | c) \(2\left| {x + 1} \right| - 0,5 = \sqrt {\dfrac{1}{9}} \) \(\begin{array}{l}2\left| {x + 1} \right| - \dfrac{1}{2} = \dfrac{1}{3}\\2\left| {x + 1} \right| = \dfrac{1}{3} + \dfrac{1}{2}\\2\left| {x + 1} \right| = \dfrac{{2 + 3}}{6} = \dfrac{5}{6}\\\left| {x + 1} \right| = \dfrac{5}{6}:2\\\left| {x + 1} \right| = \dfrac{5}{{12}}\end{array}\) Trường hợp 1: \(x + 1 = \dfrac{5}{{12}} \Rightarrow x = \dfrac{5}{{12}} - 1 = \dfrac{{ - 7}}{{12}}\) Trưởng hợp 2: \(x + 1 = \dfrac{{ - 5}}{{12}} \Rightarrow x = \dfrac{{ - 5}}{{12}} - 1 = \dfrac{{ - 17}}{{12}}\) Vậy \(x = \dfrac{{ - 7}}{{12}};x = \dfrac{{ - 17}}{{12}}\) |
Bài 3
Phương pháp:
a) Chứng minh \(\Delta OAM = \Delta OBM\left( {c.c.c} \right)\)
b) Chứng minh \(\Delta OAH = \Delta OBH\left( {c.g.c} \right) \Rightarrow HA = HB\) (hai cạnh tương ứng)
c) Chứng minh \(\Delta OHK = \Delta OHE\left( {c.g.c} \right)\)
Suy ra, \(HK = HE \Rightarrow H\) là trung điểm của \(EK\,\,\,\left( 1 \right)\)
\(\angle OHK = \angle OHE\)\( \Rightarrow OH \bot EK\) tại \(H\,\,\,\left( 2 \right)\)
Từ (1) và (2), suy ra \(OH\) là đường trung trực của \(EK\).
d) Chứng minh \(\Delta OAK = \Delta OBE\left( {c.g.c} \right)\) từ đó chứng minh được \(\angle NBK = \angle NAE\)
Chứng minh \(\Delta NBK = \Delta NHE\left( {c.c.c} \right) \Rightarrow \angle NHK = \angle NHE\) từ đó chứng minh được \(NH \bot EK\) tại \(H\)
Cách giải:
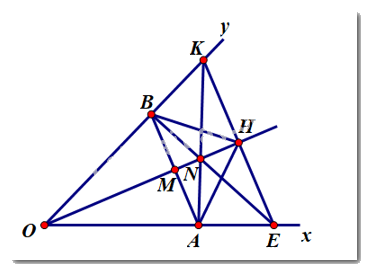
a) \(M\) là trung điểm của \(AB \Rightarrow MA = MB\)
Xét \(\Delta OAM\) và \(\Delta OBM\) có:
\(\left. \begin{array}{l}OM\,\,\,chung\\OA = OB\left( {gt} \right)\\MA = MB\left( {cmt} \right)\end{array} \right\} \Rightarrow \Delta OAM = \Delta OBM\left( {c.c.c} \right)\)
b) \(\Delta OAM = \Delta OBM\left( {cmt} \right) \Rightarrow \angle AOM = \angle BOM\) (hai góc tương ứng)
Xét \(\Delta OAH\) và \(\Delta OBH\) có:
\(\left. \begin{array}{l}OH\,\,\,chung\\\angle AOM = \angle BOM\left( {cmt} \right)\\OA = OB\left( {gt} \right)\end{array} \right\} \Rightarrow \Delta OAH = \Delta OBH\left( {c.g.c} \right) \Rightarrow HA = HB\) (hai cạnh tương ứng)
c) Ta có: \(OA = OB\left( {gt} \right) \Rightarrow \Delta OAB\) cân tại \(O \Rightarrow \angle OAB = \angle OBA\)
Vì \(AB\)//\(EK\), suy ra: \(\angle OBA = \angle OKE\) (hai góc ở vị trí đồng vị) và \(\angle OAB = \angle OEK\) (hai góc ở trí đồng vị)
Từ đó, suy ra \(\angle OKE = \angle OEK \Rightarrow \Delta OEK\) cân tại \(O \Rightarrow OK = OE\)
Xét \(\Delta OHK\) và \(\Delta OHE\) có:
\(\left. \begin{array}{l}OK = OE\left( {cmt} \right)\\\angle KOH = \angle EOH\,\left( {do\,\,\angle BOM = \angle AOM} \right)\\OH\,\,chung\end{array} \right\} \Rightarrow \Delta OHK = \Delta OHE\left( {c.g.c} \right)\)
Suy ra,
+ \(HK = HE\) (hai cạnh tương ứng) \( \Rightarrow H\)là trung điểm của \(EK\,\,\,\left( 1 \right)\)
+ \(\angle OHK = \angle OHE\) (hai góc tương ứng) mà \(\angle OHK + \angle OHE = {180^0}\) nên \(\angle OHK = \angle OHE = \dfrac{{{{180}^0}}}{2} = {90^0}\), do đó \(OH \bot EK\) tại \(H\,\,\,\left( 2 \right)\)
Từ (1) và (2), suy ra \(OH\) là đường trung trực của \(EK\).
d) Ta có: \(AE = OE - OA\,;\,\,BK = OK - OB\) mà \(OE = OK\,;\,\,OA = OB\)
Suy ra, \(AE = BK\)
Xét \(\Delta OAK\) và \(\Delta OBE\) có:
\(\left. \begin{array}{l}OA = OB\left( {cmt} \right)\\\angle O\,\,chung\\OK = OH\left( {cmt} \right)\end{array} \right\} \Rightarrow \Delta OAK = \Delta OBE\left( {c.g.c} \right)\)
Suy ra, \(\angle OKA = \angle OEB\) và \(\angle OAH = \angle OBE\) (hai góc tương ứng)
Ta có: \(\left\{ \begin{array}{l}\angle NBK = {180^0} - \angle OBE\\\angle NAE = {180^0} - \angle OAK\end{array} \right.\)
Do đó, \(\angle NBK = \angle NAE\)
Xét \(\Delta NBK\) và \(\Delta NHE\) có:
\(\left. \begin{array}{l}\angle NBK = \angle NAE\left( {cmt} \right)\\BK = AE\left( {cmt} \right)\\\angle OKA = \angle OEB\left( {cmt} \right)\end{array} \right\} \Rightarrow \Delta NBK = \Delta NHE\left( {c.c.c} \right) \Rightarrow \angle NHK = \angle NHE\) (hai góc tương ứng)
Mà \(\angle NHK + \angle NHE = {180^0}\)
\( \Rightarrow \angle NHK = \angle NHE = \dfrac{{{{180}^0}}}{2} = {90^0}\)
\( \Rightarrow NH \bot EK\) tại \(H\) mà \(OH \bot EK\) tại \(H\)
\( \Rightarrow NH \equiv OH\)
\( \Rightarrow O,N,H\) thẳng hàng
\( \Rightarrow O,M,H\) thẳng hàng.
Bài 4
Phương pháp:
Đánh giá các số hạng của tổng để tìm giá trị nhỏ nhất của \(A\).
Chú ý: \({x^2} \ge 0,\forall x \in \mathbb{R}\).
Cách giải:
Ta có: \({x^2} \ge 0;\sqrt x \ge 0\) với mọi số thực \(x \ge 0\) nên \({x^2} + 3\sqrt x \ge 0\) với mọi số thực \(x \ge 0\).
Suy ra \({x^2} + 3\sqrt x - 2024 \ge - 2024\) với mọi số thực \(x \ge 0.\) Hay \(A \ge - 2024\) với mọi số thực \(x \ge 0.\)
Dấu “=” xảy ra \( \Leftrightarrow x = 0\).
Vậy \(\min A = - 2024 \Leftrightarrow x = 0\).
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Số đối của \(\dfrac{{ - 7}}{{12}}\) là:
A. \(\dfrac{7}{{12}}\)
B. \(\dfrac{7}{{ - 12}}\)
C. \(\dfrac{{12}}{{ - 7}}\)
D. \(\dfrac{{12}}{7}\)
Câu 2: Chọn khẳng định đúng.
A. \(\dfrac{{ - 37}}{{41}} > \dfrac{{23}}{{ - 17}}\)
B. \({\left( {\dfrac{1}{3}} \right)^{12}} > {\left( {\dfrac{1}{3}} \right)^{10}}\)
C. \({\left( {2,5} \right)^6} = {\left( {0,5} \right)^{12}}\)
D. \({\left( {2,5} \right)^4} < {\left( { - 2,5} \right)^5}\)
Câu 3: Chọn đáp án sai. Nếu \(\sqrt x = \dfrac{2}{3}\) thì:
A. \(x = {\left( { - \dfrac{2}{3}} \right)^2}\)
B. \(x = - {\left( { - \dfrac{2}{3}} \right)^2}\)
C. \(x = \dfrac{4}{9}\)
D. \(x = {\left( {\dfrac{2}{3}} \right)^2}\)
Câu 4: Trong các phát biểu sau, phát biểu nào sai?
A. Giá trị tuyệt đối của một số thực là một số dương hoặc bằng 0.
B. Hai số có giá trị tuyệt đối bằng nhau là hai số bằng nhau hoặc đối nhau.
C. Hai số đối nhau có giá trị tuyệt đối bằng nhau.
D. Giá trị tuyệt đối của một số thực luôn bằng chính nó.
Câu 5: Quan sát Hình 2, có \(IK//EF\). Hãy tính giá trị của \(x\)?
A. \(x = {70^0}\)
B. \(x = {110^0}\)
C. \(x = {120^0}\)
D. \(x = {90^0}\)
Câu 6:
Cho tam giác \(ABC\) có \(AB < AC\). Tia phân giác của góc \(A\) cắt \(BC\) ở \(K\). Từ \(B\) kẻ đường vuông góc với \(AK\) tại \(H\) cắt \(AC\) ở \(D\). Chọn câu sai.
A. \(HB = AD\)
B. \(HB = HD\)
C. \(AB = AD\)
D. \(\widehat {ABH} = \widehat {ADH}\)
Câu 7: Số học sinh đăng ký học bổ trợ các Câu lạc bộ Toán, Ngữ văn, Tiếng anh của lớp 7 của một trường được biểu diễn qua biểu đồ hình quạt tròn như sau:
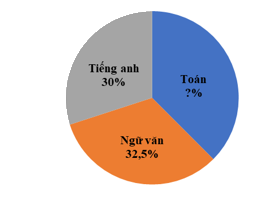
Tính số phần trăm học sinh đăng ký môn Toán là bao nhiêu?
A. 40%
B. 37,5%
C. 30%
D. 35%
Câu 8: Cho biểu đồ biểu diễn chiều cao trung bình của nam và nữ ở một số quốc gia châu Á:
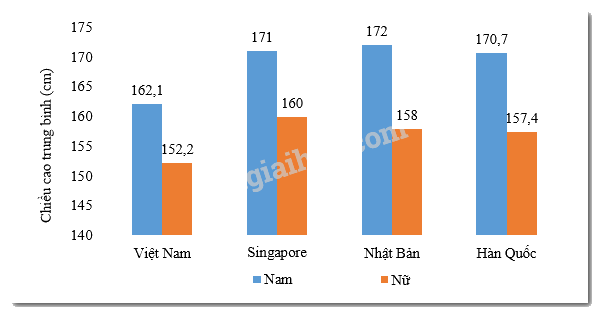
Sự chênh lệch chiều cao giữa nam và nữ của nước nào là lớn nhất?
A. Việt Nam
B. Singapore
C. Nhật Bản
D. Hàn Quốc
Câu 9: Phát biểu định lí sau bằng lời:
GT | \(a//b,c \bot a\) |
KL | \(c \bot b\) |
A. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
B. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó song song với đường thẳng kia.
C. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó tạo với đường thẳng kia một góc \({60^0}\).
D. Cả A, B, C đều đúng.
Câu 10: Vẽ \(\angle xOy = {50^0}\). Vẽ tia \(Om\) là tia phân giác của góc \(xOy\). Vẽ tia \(On\) là tia đối của tia \(Ox\). Tính góc \(mOn\).
A. \(\angle mOn = {125^0}\)
B. \(\angle mOn = {155^0}\)
C. \(\angle mOn = {160^0}\)
D. \(\angle mOn = {175^0}\)
Phần II. Tự luận (7 điểm):
Bài 1: (2,0 điểm)
Thực hiện phép tính:
a) \(\dfrac{7}{2}.\dfrac{{11}}{6} - \dfrac{7}{2}.\dfrac{5}{6}\)
b) \(\sqrt {36} - 3.\sqrt {\dfrac{1}{4}} + \left| {\dfrac{{ - 3}}{2}} \right|\)
c) \({\left( {\dfrac{{ - 1}}{2}} \right)^3} - \dfrac{7}{8}:\dfrac{7}{4} + \left| {\dfrac{{ - 9}}{8}} \right| + \sqrt {81} \)
Bài 2 (2,0 điểm).Tìm \(x\):
a) \(\dfrac{3}{5}x - \dfrac{6}{7} = \dfrac{1}{7}\)
b) \({\left( {2x - 1} \right)^3} = 64\)
c) \(2\left| {x + 1} \right| - 0,5 = \sqrt {\dfrac{1}{9}} \)
Bài 3: (3,5 điểm)
Cho góc nhọn \(xOy\), lấy điểm \(A\) trên tia \(Ox\) (điểm\(A\) khác \(O\)) và điểm \(B\) trên tia \(Oy\) sao cho \(OA = OB\). Gọi \(M\) là trung điểm của \(AB\).
a) Chứng minh: \(\Delta OAM = \Delta OBM\)
b) Trên tia \(OM\) lấy điểm \(H\) sao cho \(OM < OH\). Chứng minh \(HA = HB\).
c) Qua \(H\) kẻ đường thẳng song song với \(AB\) cắt \(Ox\) tại \(E\) cắt \(Oy\) tại \(K\). Chứng minh \(OH\) là đương trung trực của \(EK\).
d) Gọi giao điểm của \(AK\) và \(BE\) là \(N\). Chứng minh ba điểm \(O,M,N\) thẳng hàng.
Bài 4: (0,5 điểm)
Tìm giá trị nhỏ nhất của biểu thức \(A = {x^2} + 3\sqrt x - 2024\) với \(x \ge 0\).
Phần I: Trắc nghiệm:
1.A | 2.A | 3.B | 4.D | 5.D | 6.A | 7.B | 8.C | 9. A | 10.B |
Câu 1
Phương pháp:
Số đối của số hữu tỉ \(a\) kí hiệu là \( - a\).
Cách giải:
Số đối của \(\dfrac{{ - 7}}{{12}}\) là: \( - \left( {\dfrac{{ - 7}}{{12}}} \right) = \dfrac{7}{{12}}\)
Chọn A.
Câu 2
Phương pháp:
Sử dụng phương pháp so sánh trung gian.
Cách giải:
+ Ta có: \(37 < 41\) nên \(\dfrac{{37}}{{41}} < 1\) suy ra \(\dfrac{{ - 37}}{{41}} > - 1\) (1)
\(23 > 17\) nên \(\dfrac{{23}}{{17}} > 1\) suy ra \(\dfrac{{23}}{{ - 17}} < - 1\) (2)
Từ (1) và (2), suy ra \(\dfrac{{23}}{{ - 17}} < - 1 < \dfrac{{ - 37}}{{41}}\), do đó, \(\dfrac{{ - 37}}{{41}} > \dfrac{{23}}{{ - 17}}\)
Vậy đáp án A đúng.
Chọn A.
Câu 3
Phương pháp:
Căn bậc hai số học của số \(a\) không âm là số \(x\) không âm sao cho \({x^2} = a\).
Sử dụng tính chất: \({x^2} = {\left( { - x} \right)^2}\)
Cách giải:
\(\sqrt {{{\left( { - \dfrac{2}{3}} \right)}^2}} = \sqrt {{{\left( {\dfrac{2}{3}} \right)}^2}} = \sqrt {\dfrac{4}{9}} = \dfrac{2}{3}\) nên đáp án A,C,D đúng
Do chỉ tồn tại căn bậc hai số học của một số không âm nên đáp án B sai.
Chọn B.
Câu 4
Phương pháp:
Vận dụng kiến thức giá trị tuyệt đối của một số thực, tìm phát biểu sai.
Cách giải:
Phát biểu A đúng vì giá trị tuyệt đối của một số thực là một số không âm.
Phát biểu B đúng vì hai số có giá trị tuyệt đối bằng nhau là hai số bằng nhau hoặc đối nhau.
Phát biểu C đúng vì hai số đối nhau có điểm biểu diễn cách đều điểm gốc 0 nên giá trị tuyệt đối của chúng bằng nhau.
Phát biểu D sai vì giá trị tuyệt đối của số âm là số đối của nó.
Chọn D.
Câu 5
Phương pháp:
Hai góc kề bù có tổng số đo bằng \({180^0}\)
Hai đường thẳng song song thì hai góc ở vị trí đồng vị bằng nhau.
Vận dụng định lý: Tổng ba góc trong một tam giác bằng \({180^0}\).
Cách giải:
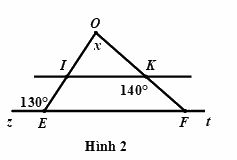
* Ta có: \(\angle zEO + \angle OEF = {180^0}\) (hai góc kề bù)
\(\begin{array}{l} \Rightarrow {130^0} + \angle OEF = {180^0}\\ \Rightarrow \angle OEF = {180^0} - {130^0}\\ \Rightarrow \angle OEF = {50^0}\end{array}\)
* \(IK//EF\) (giá thiết) \( \Rightarrow \angle OEF = \angle OIK\) (hai góc đồng vị) do đó, \(\angle OIK = {50^0}\)
* Ta có: \(\angle IKO + \angle IKF = {180^0}\) (hai góc kề bù)
\(\begin{array}{l} \Rightarrow \angle IKO + {140^0} = {180^0}\\ \Rightarrow \angle IKO = {180^0} - {140^0}\\ \Rightarrow \angle IKO = {40^0}\end{array}\)
* Xét \(\Delta OIK\) có: \(\angle O + \angle OIK + \angle OKI = {180^0}\) (định lí tổng ba góc trong một tam giác)
\(\begin{array}{l} \Rightarrow x + {50^0} + {40^0} = {180^0}\\ \Rightarrow x + {90^0} = {180^0}\\ \Rightarrow x = {180^0} - {90^0}\\ \Rightarrow x = {90^0}\end{array}\)
Vậy \(x = {90^0}\)
Chọn D.
Câu 6
Phương pháp:
+ Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
+ Hai tam giác bằng nhau có các cặp cạnh, cặp góc tương ứng bằng nhau
Cách giải:
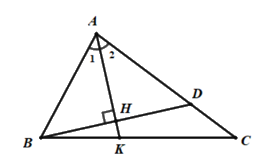
Vì \(AK\) là tia phân giác của \(\angle BAC\) nên \(\angle {A_1} = \angle {A_2}\)
Theo giả thiết ta có: \(BH \bot AK \Rightarrow \angle AHB = \angle AHD = 90^\circ \)
Xét tam giác \(AHB\) và tam giác \(AHD\) có:
\(\angle {A_1} = \angle {A_2}\)
\(AH\) là cạnh chung
\(\angle AHB = \angle AHD = 90^\circ \)
Nên \(\Delta AHB = \Delta AHD\) (g.c.g)
Suy ra: \(HB = HD\) (hai cạnh tương ứng) nên B đúng
\(AB = AD\) (hai cạnh tương ứng) nên C đúng
\(\angle ABH = \angle ADH\) (hai góc tương ứng) nên D đúng
Chọn A.
Câu 7
Phương pháp:
Đọc và phân tích dữ liệu của biểu đồ hình quạt tròn.
Cách giải:
Số phần trăm học sinh đăng ký môn Toán là: \(100\% - 32,5\% - 30\% = 37,5\% \)
Chọn B.
Câu 8
Phương pháp:
Sử dụng biểu đồ cột kép, quan sát và trả lời câu hỏi.
Cách giải:
*) Chiều cao trung bình của nam:
Việt Nam: \(162,1cm\)
Singapore: \(171cm\)
Nhật Bản: \(172cm\)
Hàn Quốc: \(170,7cm\)
*) Chiều cao trung bình của nữ:
Việt Nam: \(152,2cm\)
Singapore:\(160cm\)
Nhật Bản: \(158cm\)
Hàn Quốc: \(157,4cm\)
Sự chênh lệch chiều cao giữa nam và nữ ở Việt Nam là:
\(162,1 - 152,2 = 9,9\,\,\left( {cm} \right)\)
Sự chênh lệch chiều cao giữa nam và nữ ở Singapore là:
\(171 - 160 = 11\,\,\left( {cm} \right)\)
Sự chênh lệch chiều cao giữa nam và nữ ở Nhật Bản là:
\(172 - 158 = 14\,\,\left( {cm} \right)\)
Sự chênh lệch chiều cao giữa nam và nữ ở Hàn Quốc là:
\(170,7 - 157,4 = 13,3\,\,\left( {cm} \right)\)
Sự chênh lệch chiều cao giữa nam và nữ ở Nhật Bản là lớn nhất.
Chọn C.
Câu 9
Phương pháp:
Định lí là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … thì ….
Cách giải:
Phát biểu định lí: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
Chọn A.
Câu 10
Phương pháp
\(Oz\) là tia phân giác của \(\angle xOy\) thì ta có: \(\angle xOz = \angle zOy = \dfrac{{\angle xOy}}{2}\)
\(\angle xOz\) và \(\angle zOy\) là hai góc kề nhau thì ta có: \(\angle xOz + \angle zOy = \angle xOy\).
\(\angle xOz\) và \(\angle zOy\) là hai góc kề bù thì ta có: \(\angle xOy = \angle xOz + \angle zOy = {180^0}\)
Cách giải:
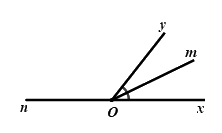
Vì \(Om\) là tia phân giác của \(\angle xOy\) nên \(\angle mOy = \dfrac{{\angle xOy}}{2} = \dfrac{{{{50}^0}}}{2} = {25^0}\)
Ta có: \(\angle nOy\) và \(\angle yOx\) là hai góc kề bù nên \(\angle nOy + \angle yOx = {180^0}\)
\(\begin{array}{l} \Rightarrow \angle nOy + {50^0} = {180^0}\\ \Rightarrow \angle nOy = {180^0} - {50^0} = {130^0}\end{array}\)
Ta có: \(\angle nOy\) và \(\angle yOm\) là hai góc kề nhau nên \(\angle nOy + \angle yOm = \angle nOm\)
\( \Rightarrow {130^0} + {25^0} = {155^0} = \angle nOm\)
Vậy \(\angle mOn = {155^0}\)
Chọn B.
Phần II. Tự luận (7 điểm):
Bài 1
Phương pháp:
Thực hiện phép tính với số hữu tỉ, giá trị tuyệt đối của một số hữu tỉ.
Cách giải:
a) \(\dfrac{7}{2}.\dfrac{{11}}{6} - \dfrac{7}{2}.\dfrac{5}{6}\) \(\begin{array}{l} = \dfrac{7}{2}.\left( {\dfrac{{11}}{6} + \dfrac{5}{6}} \right)\\ = \dfrac{7}{2}.\dfrac{{16}}{6}\\ = \dfrac{{28}}{3}\end{array}\) | b) \(\sqrt {36} - 3.\sqrt {\dfrac{1}{4}} + \left| {\dfrac{{ - 3}}{2}} \right|\) \(\begin{array}{l} = 6 - 3.\dfrac{1}{2} + \dfrac{3}{2}\\ = 6 + \left( {\dfrac{3}{2} - \dfrac{3}{2}} \right)\\ = 6 + 0 = 6\end{array}\) | c) \({\left( {\dfrac{{ - 1}}{2}} \right)^3} - \dfrac{7}{8}:\dfrac{7}{4} + \left| {\dfrac{{ - 9}}{8}} \right| + \sqrt {81} \) \(\begin{array}{l} = \dfrac{{ - 1}}{8} - \dfrac{7}{8}.\dfrac{4}{7} + \dfrac{9}{8} + 9\\ = \left( { - \dfrac{1}{8} + \dfrac{9}{8}} \right) - \dfrac{1}{2} + 9\\ = 1 - \dfrac{1}{2} + 9\\ = \dfrac{1}{2} + 9 = \dfrac{{19}}{2}\end{array}\) |
Bài 2
Phương pháp:
Thực hiện phép tính với số hữu tỉ, giá trị tuyệt đối của một số hữu tỉ.
Cách giải:
a) \(\dfrac{3}{5}x - \dfrac{6}{7} = \dfrac{1}{7}\) \(\begin{array}{l}\dfrac{3}{5}x = \dfrac{1}{7} + \dfrac{6}{7}\\\dfrac{3}{5}x = \dfrac{7}{7} = 1\\x = 1:\dfrac{3}{5}\\x = \dfrac{5}{3}\end{array}\) Vậy \(x = \dfrac{5}{3}\) | b) \({\left( {2x - 1} \right)^3} = 64\) \(\begin{array}{l}{\left( {2x - 1} \right)^3} = {4^3}\\2x - 1 = 4\\2x = 4 + 1\\2x = 5\\x = \dfrac{5}{2}\end{array}\) Vậy \(x = \dfrac{5}{2}\) | c) \(2\left| {x + 1} \right| - 0,5 = \sqrt {\dfrac{1}{9}} \) \(\begin{array}{l}2\left| {x + 1} \right| - \dfrac{1}{2} = \dfrac{1}{3}\\2\left| {x + 1} \right| = \dfrac{1}{3} + \dfrac{1}{2}\\2\left| {x + 1} \right| = \dfrac{{2 + 3}}{6} = \dfrac{5}{6}\\\left| {x + 1} \right| = \dfrac{5}{6}:2\\\left| {x + 1} \right| = \dfrac{5}{{12}}\end{array}\) Trường hợp 1: \(x + 1 = \dfrac{5}{{12}} \Rightarrow x = \dfrac{5}{{12}} - 1 = \dfrac{{ - 7}}{{12}}\) Trưởng hợp 2: \(x + 1 = \dfrac{{ - 5}}{{12}} \Rightarrow x = \dfrac{{ - 5}}{{12}} - 1 = \dfrac{{ - 17}}{{12}}\) Vậy \(x = \dfrac{{ - 7}}{{12}};x = \dfrac{{ - 17}}{{12}}\) |
Bài 3
Phương pháp:
a) Chứng minh \(\Delta OAM = \Delta OBM\left( {c.c.c} \right)\)
b) Chứng minh \(\Delta OAH = \Delta OBH\left( {c.g.c} \right) \Rightarrow HA = HB\) (hai cạnh tương ứng)
c) Chứng minh \(\Delta OHK = \Delta OHE\left( {c.g.c} \right)\)
Suy ra, \(HK = HE \Rightarrow H\) là trung điểm của \(EK\,\,\,\left( 1 \right)\)
\(\angle OHK = \angle OHE\)\( \Rightarrow OH \bot EK\) tại \(H\,\,\,\left( 2 \right)\)
Từ (1) và (2), suy ra \(OH\) là đường trung trực của \(EK\).
d) Chứng minh \(\Delta OAK = \Delta OBE\left( {c.g.c} \right)\) từ đó chứng minh được \(\angle NBK = \angle NAE\)
Chứng minh \(\Delta NBK = \Delta NHE\left( {c.c.c} \right) \Rightarrow \angle NHK = \angle NHE\) từ đó chứng minh được \(NH \bot EK\) tại \(H\)
Cách giải:
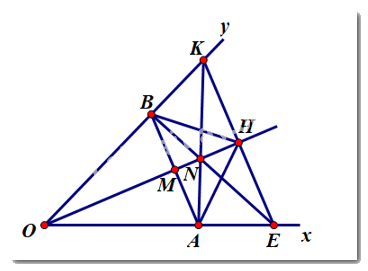
a) \(M\) là trung điểm của \(AB \Rightarrow MA = MB\)
Xét \(\Delta OAM\) và \(\Delta OBM\) có:
\(\left. \begin{array}{l}OM\,\,\,chung\\OA = OB\left( {gt} \right)\\MA = MB\left( {cmt} \right)\end{array} \right\} \Rightarrow \Delta OAM = \Delta OBM\left( {c.c.c} \right)\)
b) \(\Delta OAM = \Delta OBM\left( {cmt} \right) \Rightarrow \angle AOM = \angle BOM\) (hai góc tương ứng)
Xét \(\Delta OAH\) và \(\Delta OBH\) có:
\(\left. \begin{array}{l}OH\,\,\,chung\\\angle AOM = \angle BOM\left( {cmt} \right)\\OA = OB\left( {gt} \right)\end{array} \right\} \Rightarrow \Delta OAH = \Delta OBH\left( {c.g.c} \right) \Rightarrow HA = HB\) (hai cạnh tương ứng)
c) Ta có: \(OA = OB\left( {gt} \right) \Rightarrow \Delta OAB\) cân tại \(O \Rightarrow \angle OAB = \angle OBA\)
Vì \(AB\)//\(EK\), suy ra: \(\angle OBA = \angle OKE\) (hai góc ở vị trí đồng vị) và \(\angle OAB = \angle OEK\) (hai góc ở trí đồng vị)
Từ đó, suy ra \(\angle OKE = \angle OEK \Rightarrow \Delta OEK\) cân tại \(O \Rightarrow OK = OE\)
Xét \(\Delta OHK\) và \(\Delta OHE\) có:
\(\left. \begin{array}{l}OK = OE\left( {cmt} \right)\\\angle KOH = \angle EOH\,\left( {do\,\,\angle BOM = \angle AOM} \right)\\OH\,\,chung\end{array} \right\} \Rightarrow \Delta OHK = \Delta OHE\left( {c.g.c} \right)\)
Suy ra,
+ \(HK = HE\) (hai cạnh tương ứng) \( \Rightarrow H\)là trung điểm của \(EK\,\,\,\left( 1 \right)\)
+ \(\angle OHK = \angle OHE\) (hai góc tương ứng) mà \(\angle OHK + \angle OHE = {180^0}\) nên \(\angle OHK = \angle OHE = \dfrac{{{{180}^0}}}{2} = {90^0}\), do đó \(OH \bot EK\) tại \(H\,\,\,\left( 2 \right)\)
Từ (1) và (2), suy ra \(OH\) là đường trung trực của \(EK\).
d) Ta có: \(AE = OE - OA\,;\,\,BK = OK - OB\) mà \(OE = OK\,;\,\,OA = OB\)
Suy ra, \(AE = BK\)
Xét \(\Delta OAK\) và \(\Delta OBE\) có:
\(\left. \begin{array}{l}OA = OB\left( {cmt} \right)\\\angle O\,\,chung\\OK = OH\left( {cmt} \right)\end{array} \right\} \Rightarrow \Delta OAK = \Delta OBE\left( {c.g.c} \right)\)
Suy ra, \(\angle OKA = \angle OEB\) và \(\angle OAH = \angle OBE\) (hai góc tương ứng)
Ta có: \(\left\{ \begin{array}{l}\angle NBK = {180^0} - \angle OBE\\\angle NAE = {180^0} - \angle OAK\end{array} \right.\)
Do đó, \(\angle NBK = \angle NAE\)
Xét \(\Delta NBK\) và \(\Delta NHE\) có:
\(\left. \begin{array}{l}\angle NBK = \angle NAE\left( {cmt} \right)\\BK = AE\left( {cmt} \right)\\\angle OKA = \angle OEB\left( {cmt} \right)\end{array} \right\} \Rightarrow \Delta NBK = \Delta NHE\left( {c.c.c} \right) \Rightarrow \angle NHK = \angle NHE\) (hai góc tương ứng)
Mà \(\angle NHK + \angle NHE = {180^0}\)
\( \Rightarrow \angle NHK = \angle NHE = \dfrac{{{{180}^0}}}{2} = {90^0}\)
\( \Rightarrow NH \bot EK\) tại \(H\) mà \(OH \bot EK\) tại \(H\)
\( \Rightarrow NH \equiv OH\)
\( \Rightarrow O,N,H\) thẳng hàng
\( \Rightarrow O,M,H\) thẳng hàng.
Bài 4
Phương pháp:
Đánh giá các số hạng của tổng để tìm giá trị nhỏ nhất của \(A\).
Chú ý: \({x^2} \ge 0,\forall x \in \mathbb{R}\).
Cách giải:
Ta có: \({x^2} \ge 0;\sqrt x \ge 0\) với mọi số thực \(x \ge 0\) nên \({x^2} + 3\sqrt x \ge 0\) với mọi số thực \(x \ge 0\).
Suy ra \({x^2} + 3\sqrt x - 2024 \ge - 2024\) với mọi số thực \(x \ge 0.\) Hay \(A \ge - 2024\) với mọi số thực \(x \ge 0.\)
Dấu “=” xảy ra \( \Leftrightarrow x = 0\).
Vậy \(\min A = - 2024 \Leftrightarrow x = 0\).
Đề thi học kì 1 Toán 7 - Đề số 7 chương trình Kết nối tri thức là một bài kiểm tra quan trọng, đánh giá mức độ nắm vững kiến thức và kỹ năng của học sinh sau một học kỳ học tập. Đề thi bao gồm các dạng bài tập khác nhau, từ trắc nghiệm đến tự luận, tập trung vào các chủ đề chính như số hữu tỉ, số thực, biểu thức đại số, phương trình bậc nhất một ẩn, bất đẳng thức và các ứng dụng thực tế của Toán học.
Thông thường, đề thi học kì 1 Toán 7 - Đề số 7 - Kết nối tri thức sẽ được chia thành các phần sau:
Để đạt kết quả tốt trong kỳ thi học kì 1 Toán 7, học sinh cần:
Bài 1: (Trắc nghiệm) Giá trị của biểu thức 2x + 3y khi x = 1 và y = -1 là:
A. 1
B. -1
C. 0
D. 2
Lời giải: Thay x = 1 và y = -1 vào biểu thức, ta có: 2(1) + 3(-1) = 2 - 3 = -1. Vậy đáp án đúng là B.
Để hỗ trợ học sinh ôn thi hiệu quả, giaitoan.edu.vn cung cấp:
Hãy dành thời gian ôn tập kiến thức một cách nghiêm túc và có kế hoạch. Đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè nếu gặp khó khăn. Chúc các em học sinh đạt kết quả tốt nhất trong kỳ thi học kì 1 Toán 7!
| Dạng bài tập | Ví dụ |
|---|---|
| Tính toán với số hữu tỉ | Tính: (1/2) + (2/3) - (1/4) |
| Giải phương trình bậc nhất một ẩn | Giải phương trình: 2x + 5 = 11 |
| Chứng minh bất đẳng thức | Chứng minh: a^2 + b^2 ≥ 2ab |