Chào mừng các em học sinh lớp 7 đến với đề thi giữa kì 1 Toán 7 - Đề số 2 chương trình Kết nối tri thức.
Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong giai đoạn đầu của năm học.
Giaitoan.edu.vn cung cấp đề thi chính thức, đáp án chi tiết và lời giải bài tập để hỗ trợ các em học tập tốt nhất.
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
A. PHẦN TRẮC NGHIỆM
1. C | 2. D | 3. A | 4. A | 5. D | 6. C |
Câu 1
Phương pháp
Định nghĩa số hữu tỉ
Cách giải
Số hữu tỉ là các số viết được dưới dạng \(\dfrac{a}{b}\left( {a,b \in Z,b \ne 0} \right)\)
Chọn C.
Câu 2
Phương pháp
Nếu A = B2 thì A = B hoặc A = -B
Cách giải
Ta có:
\(\begin{array}{l} - 8{x^2} + 50 = 0\\ 8{x^2} = 50\\ {x^2} = \dfrac{{50}}{8} = \dfrac{{25}}{4}\\ {x^2} = {\left( { \pm \dfrac{5}{2}} \right)^2}\\ \left[ {\begin{array}{*{20}{c}}{x = \dfrac{5}{2}}\\{x = - \dfrac{5}{2}}\end{array}} \right.\end{array}\)
Vậy \(x = \pm \dfrac{5}{2}\)
Chọn D.
Câu 3
Phương pháp
Đưa các thừa số về dạng lũy thừa có cơ số là số nguyên tố rồi rút gọn
Cách giải
Ta có:
\(\dfrac{{{3^5}{{.4}^3}}}{{{9^2}{{.8}^2}}} = \dfrac{{{3^5}.{{\left( {{2^2}} \right)}^3}}}{{{{\left( {{3^2}} \right)}^2}.{{\left( {{2^3}} \right)}^2}}} = \dfrac{{{3^5}{{.2}^{2.3}}}}{{{3^{2.2}}{{.2}^{3.2}}}} = \dfrac{{{3^5}{{.2}^6}}}{{{3^4}{{.2}^6}}} = 3\)
Chọn A.
Câu 4
Phương pháp
Xác định các góc tạo bởi 1 đường thẳng cắt 2 đường thẳng
Cách giải
2 góc A1 và B3 ở vị trí so le trong
Chọn A.
Câu 5
Phương pháp
Sử dụng tính chất tia phân giác của một góc.
Tổng số đo của 2 góc kề bù là 180 độ
Cách giải
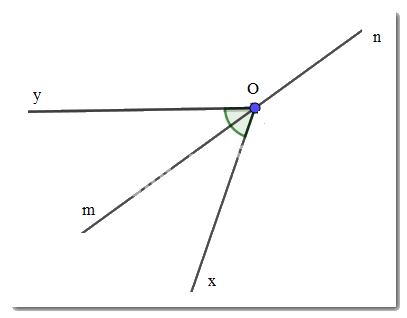
Vì Om là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOm} = \widehat {yOm} = \dfrac{1}{2}.\widehat {xOy} = \dfrac{1}{2}.70^\circ = 35^\circ \)
Mà \(\widehat {xOm},\widehat {xOn}\) là 2 góc kề bù nên \(\widehat {xOm} + \widehat {xOn} = 180^\circ \Rightarrow \widehat {xOn} = 180^\circ - \widehat {xOm} = 180^\circ - 35^\circ = 145^\circ \)
Chọn D.
Câu 6
Phương pháp
Tiên đề Euclid về đường thẳng song song
Cách giải
Theo Tiên đề Euclid về đường thẳng song song: Qua 1 điểm nằm ngoài đường thẳng, có 1 và chỉ 1 đường thẳng song song với đường thẳng đó.
Chọn A.
B. PHẦN TỰ LUẬN
Câu 1
Phương pháp:
a) Sử dụng tính chất phân phối của phép nhân và cộng \(ab + ac = a\left( {b + c} \right)\).
b) Đưa về phân số và tính toán.
Cách giải:
a)
\(\begin{array}{*{20}{l}}{{\mkern 1mu} {\mkern 1mu} \dfrac{4}{{13}}.15\dfrac{3}{{41}} - \dfrac{4}{{13}}.2\dfrac{3}{{41}}}\\{ = \dfrac{4}{{13}}\left( {15\dfrac{3}{{41}} - 2\dfrac{3}{{41}}} \right)}\\{ = \dfrac{4}{{13}}.13}\\{ = 4}\end{array}\)
b)
\(\begin{array}{*{20}{l}}{{\mkern 1mu} {\mkern 1mu} \sqrt {25} .\left( {0,4 - 1\dfrac{1}{2}} \right):\left[ {{{\left( { - 2} \right)}^3}.\dfrac{{11}}{8}} \right]}\\{ = 5.\left( {\dfrac{2}{5} - \dfrac{3}{2}} \right):\left( { - 8.\dfrac{{11}}{8}} \right)}\\{ = 5.\left( {\dfrac{4}{{10}} - \dfrac{{15}}{{10}}} \right):\left( { - 11} \right)}\\{ = 5.\dfrac{{ - 11}}{{10}}.\dfrac{{ - 1}}{{11}}}\\{ = \dfrac{1}{2}}\end{array}\)
Câu 2
Phương pháp
a) Đưa các số hữu tỉ về dạng phân số
Số trừ = số bị trừ - hiệu
b) Đưa 2 tỉ số về dạng có cùng mẫu số rồi sử dụng nhận xét: Nếu \(\dfrac{a}{b} = \dfrac{c}{b} \Rightarrow a = c(b \ne 0)\)
c) Nếu A . B = 0 thì A = 0 hoặc B = 0
Lời giải
a)
\(\begin{array}{l} - 0,12 - 2x = - 1\dfrac{2}{5}\\ \dfrac{{ - 12}}{{100}} - 2x = \dfrac{{ - 7}}{5}\\ \dfrac{{ - 3}}{{25}} - 2x = \dfrac{{ - 7}}{5}\\ 2x = \dfrac{{ - 3}}{{25}} - (\dfrac{{ - 7}}{5})\\ 2x = \dfrac{{ - 3}}{{25}} + \dfrac{{35}}{{25}}\\ 2x = \dfrac{{32}}{{25}}\\ x = \dfrac{{32}}{{25}}:2\\ x = \dfrac{{32}}{{25}}.\dfrac{1}{2}\\ x = \dfrac{{16}}{{25}}\end{array}\)
Vậy \(x = \dfrac{{16}}{{25}}\)
b)
\(\begin{array}{l}\dfrac{{x + \dfrac{3}{2}}}{6} = \dfrac{{ - 5}}{{12}}\\ \dfrac{{2.(x + \dfrac{3}{2})}}{{12}} = \dfrac{{ - 5}}{{12}}\\ \dfrac{{2x + 3}}{{12}} = \dfrac{{ - 5}}{{12}}\\ 2x + 3 = - 5\\ 2x = - 5 - 3\\ 2x = - 8\\ x = - 4\end{array}\)
Vậy x = -4
c)
\(\left( { - 2x + \dfrac{5}{2}} \right).\left( {{x^2} + 4} \right) = 0\)
+) Trường hợp 1:
\(\begin{array}{*{20}{l}}{ - 2x + \dfrac{5}{2} = 0}\\{ 2x = \dfrac{5}{2}}\\{ x = \dfrac{5}{2}:2}\\{ x = \dfrac{5}{4}}\end{array}\)
+) Trường hợp 2:
x2 + 4 = 0
\( {x^2} = - 4\) ( Vô lí vì x2 \( \ge \)0 với mọi x)
Vậy x = \(\dfrac{5}{4}\)
Câu 3
Phương pháp:
+ Áp dụng tính chất: Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau.
+ Dấu hiệu nhận biết hai đường thẳng song song.
Cách giải:
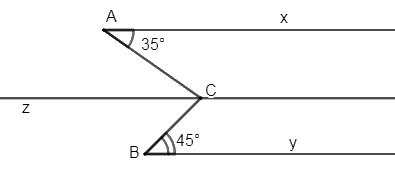
Kẻ \(Cz//{\rm{Ax}} \Rightarrow \widehat {xAC} = \widehat {ACz} = {35^0}\) (so le trong)
Ta có:
\(\widehat {ACz} + \widehat {zCB} = \widehat {ACB} \Rightarrow \widehat {zCB} = \widehat {ACB} - \widehat {ACz} = {80^0} - {35^0} = {45^0}\)
\( \Rightarrow \widehat {zCB} = \widehat {CBy}\left( { = {{45}^0}} \right)\)
Mà hai góc ở vị trí so le trong nên suy ra \(Cz//{\mkern 1mu} By\) (dấu hiệu nhận biết hai đường thẳng song song)
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{Cz//{\mkern 1mu} Ax\left( {gt} \right)}\\{C{\rm{z}}//{\mkern 1mu} By\left( {cmt} \right)}\end{array}} \right. \Rightarrow Ax//{\mkern 1mu} By\) .
Câu 4
Phương pháp
Xét hình tròn bán kính R:
Diện tích hình tròn = 3,14 . R2 , suy ra R
Chu vi hình tròn = 3,14 . R
Cách giải
Ta có: S = 3.14 . R2 hay 200 = 3,14. R2 . Do đó, \({R^2} = \dfrac{{200}}{{3,14}} \approx 63,7 \Rightarrow R = \sqrt {63,7} \approx 7,98(m)\)
Chu vi hình tròn đó là: C = 3,14 . R \( \approx \) 3,14 . 7,98 \( \approx \) 25,0572 (m)
Làm tròn 25,0572 với độ chính xác 0,05, tức là làm tròn đến chữ số thập phân thứ nhất.
Vì chữ số hàng làm tròn là 0, chữ số ngay sau hàng làm tròn là 5 nên ta cộng thêm 1 đơn vị vào chữ số hàng làm tròn, đồng thời bỏ đi các chữ số ở sau hàng làm tròn.
Ta được kết quả chu vi sân đấu làm tròn là 25,1 (m)
Câu 5
Phương pháp
Áp dụng tính chất hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
- Tính chất hai đường thẳng song song.
Cách giải
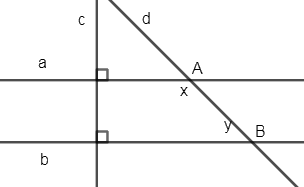
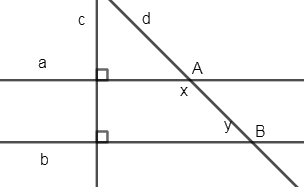
Vì \(a \bot c,{\mkern 1mu} b \bot c\left( {gt} \right) \Rightarrow a//{\mkern 1mu} b \Rightarrow \widehat {aAB} + \widehat {ABb} = {180^0} \Rightarrow x + y = {180^0}\)(2 góc trong cùng phía bù nhau)
\( \Rightarrow x = {180^0} - y\)
Lại có:
\(\begin{array}{*{20}{l}}{2{\rm{x}} = 3y\left( {gt} \right) \Rightarrow 2\left( {{{180}^0} - y} \right) = 3y}\\{ {{360}^0} - 2y = 3y}\\{ 5y = {{360}^0} \Rightarrow y = {{360}^0}:5 = {{72}^0}}\\{ \Rightarrow x = {{180}^0} - {{72}^0} = {{108}^0}}\end{array}\)
Câu 6
Phương pháp:
Đánh giá giá trị của tử và mẫu
Chú ý: a4 \( \ge \) 0, với mọi a
Cách giải:
Vì (2x+1)4 \( \ge \) 0, với mọi x nên (2x+1)4 +2 \( \ge \) 2, với mọi x
\( \Rightarrow \dfrac{3}{{{{(2x + 1)}^4} + 2}} \le \dfrac{3}{2}\), với mọi x. Dấu “=” xảy ra khi 2x + 1 = 0 hay x = \(\dfrac{{ - 1}}{2}\)
Vậy Max M = \(\dfrac{3}{2}\).
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1:Số hữu tỉ là:
A. Phân số khác 0
B. Các số viết được dưới dạng \(\dfrac{a}{b}\left( {a,b \in N,b \ne 0} \right)\)
C. Các số viết được dưới dạng \(\dfrac{a}{b}\left( {a,b \in Z,b \ne 0} \right)\)
D. Các số viết được dưới dạng \(\dfrac{a}{b}\left( {a,b \in Z} \right)\)
Câu 2: Giá trị x thỏa mãn \( - 8{x^2} + 50 = 0\)là:
A. \(x = \dfrac{{25}}{4}\);
B. \(x = \dfrac{5}{2}\);
C. \(x = \dfrac{{ - 5}}{2}\);
D. \(x = \pm \dfrac{5}{2}\).
Câu 3: Kết quả của phép tính \(\dfrac{{{3^5}{{.4}^3}}}{{{9^2}{{.8}^2}}}\)là
A. \(3\);
B. \(1\);
C. \(\dfrac{3}{4}\);
D. Một kết quả khác.
Câu 4: Trên hình vẽ, 2 góc A1 và B3 ở vị trí:
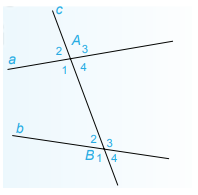
A. so le trong;
B. so le ngoài;
C. đồng vị;
D. trong cùng phía.
Câu 5:Cho \(\widehat {xOy} = 70^\circ \). Tia Om là tia phân giác của \(\widehat {xOy}\), tia On là tia đối của tia Om. Tính số đo \(\widehat {xOn}\)
A.\(70^\circ \);
B.\(\;35^\circ \);
C. \(110^\circ \);
D. \(145^\circ \).
Câu 6:Cho điểm A nằm ngoài đường thẳng p. Có bao nhiêu đường thẳng song song với d, đi qua A?
A. \(0\);
B. \(2\);
C. \(1\);
D. Vô số.
B. PHẦN TỰ LUẬN (7 điểm)
Câu 1: ( 1 điểm)
Tính giá trị của các biểu thức sau:
a) \({\mkern 1mu} {\mkern 1mu} \dfrac{4}{{13}}.15\dfrac{3}{{41}} - \dfrac{4}{{13}}.2\dfrac{3}{{41}}\)
b) \({\mkern 1mu} {\mkern 1mu} \sqrt {25} .\left( {0,4 - 1\dfrac{1}{2}} \right):\left[ {{{\left( { - 2} \right)}^3}.\dfrac{{11}}{8}} \right]\)
Câu 2: (1,5 điểm)
Tìm x, biết:
a) \( - 0,12 - 2x = - 1\dfrac{2}{5}\)
b) \(\dfrac{{x + \dfrac{3}{2}}}{6} = \dfrac{{ - 5}}{{12}}\)
c) \(\left( { - 2x + \dfrac{5}{2}} \right).\left( {{x^2} + 4} \right) = 0\)
Câu 3: ( 1,5 điểm)
Cho hình vẽ sau:
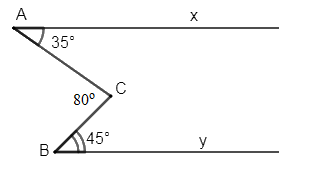
Biết \(\widehat {xAC} = {35^0},{\mkern 1mu} \widehat {CBy} = {45^0}\) và \(\widehat {ACB} = {80^0}.\) Chứng minh rằng \(Ax{\mkern 1mu} //{\mkern 1mu} By\).
Câu 4: (1 điểm)
Tính chu vi một sân đấu hình tròn biết diện tích của nó là 200 m2 (làm tròn kết quả với độ chính xác 0,05)
Câu 5: ( 1,5 điểm)
Cho hình vẽ sau:
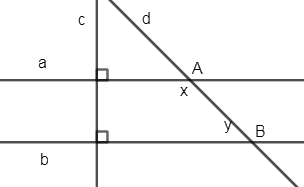
Biết \(a \bot c,{\mkern 1mu} b \bot c,{\mkern 1mu} 2{\rm{x}} = 3y\). Tính x, y.
Câu 6: (0,5 điểm)Tìm giá trị lớn nhất của biểu thức:
\(M = \dfrac{3}{{{{(2x + 1)}^4} + 2}}\)
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1:Số hữu tỉ là:
A. Phân số khác 0
B. Các số viết được dưới dạng \(\dfrac{a}{b}\left( {a,b \in N,b \ne 0} \right)\)
C. Các số viết được dưới dạng \(\dfrac{a}{b}\left( {a,b \in Z,b \ne 0} \right)\)
D. Các số viết được dưới dạng \(\dfrac{a}{b}\left( {a,b \in Z} \right)\)
Câu 2: Giá trị x thỏa mãn \( - 8{x^2} + 50 = 0\)là:
A. \(x = \dfrac{{25}}{4}\);
B. \(x = \dfrac{5}{2}\);
C. \(x = \dfrac{{ - 5}}{2}\);
D. \(x = \pm \dfrac{5}{2}\).
Câu 3: Kết quả của phép tính \(\dfrac{{{3^5}{{.4}^3}}}{{{9^2}{{.8}^2}}}\)là
A. \(3\);
B. \(1\);
C. \(\dfrac{3}{4}\);
D. Một kết quả khác.
Câu 4: Trên hình vẽ, 2 góc A1 và B3 ở vị trí:
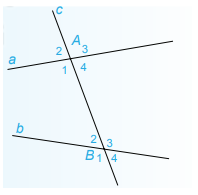
A. so le trong;
B. so le ngoài;
C. đồng vị;
D. trong cùng phía.
Câu 5:Cho \(\widehat {xOy} = 70^\circ \). Tia Om là tia phân giác của \(\widehat {xOy}\), tia On là tia đối của tia Om. Tính số đo \(\widehat {xOn}\)
A.\(70^\circ \);
B.\(\;35^\circ \);
C. \(110^\circ \);
D. \(145^\circ \).
Câu 6:Cho điểm A nằm ngoài đường thẳng p. Có bao nhiêu đường thẳng song song với d, đi qua A?
A. \(0\);
B. \(2\);
C. \(1\);
D. Vô số.
B. PHẦN TỰ LUẬN (7 điểm)
Câu 1: ( 1 điểm)
Tính giá trị của các biểu thức sau:
a) \({\mkern 1mu} {\mkern 1mu} \dfrac{4}{{13}}.15\dfrac{3}{{41}} - \dfrac{4}{{13}}.2\dfrac{3}{{41}}\)
b) \({\mkern 1mu} {\mkern 1mu} \sqrt {25} .\left( {0,4 - 1\dfrac{1}{2}} \right):\left[ {{{\left( { - 2} \right)}^3}.\dfrac{{11}}{8}} \right]\)
Câu 2: (1,5 điểm)
Tìm x, biết:
a) \( - 0,12 - 2x = - 1\dfrac{2}{5}\)
b) \(\dfrac{{x + \dfrac{3}{2}}}{6} = \dfrac{{ - 5}}{{12}}\)
c) \(\left( { - 2x + \dfrac{5}{2}} \right).\left( {{x^2} + 4} \right) = 0\)
Câu 3: ( 1,5 điểm)
Cho hình vẽ sau:
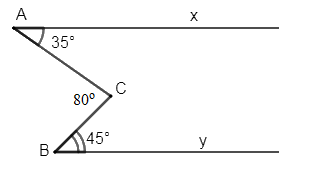
Biết \(\widehat {xAC} = {35^0},{\mkern 1mu} \widehat {CBy} = {45^0}\) và \(\widehat {ACB} = {80^0}.\) Chứng minh rằng \(Ax{\mkern 1mu} //{\mkern 1mu} By\).
Câu 4: (1 điểm)
Tính chu vi một sân đấu hình tròn biết diện tích của nó là 200 m2 (làm tròn kết quả với độ chính xác 0,05)
Câu 5: ( 1,5 điểm)
Cho hình vẽ sau:
Biết \(a \bot c,{\mkern 1mu} b \bot c,{\mkern 1mu} 2{\rm{x}} = 3y\). Tính x, y.
Câu 6: (0,5 điểm)Tìm giá trị lớn nhất của biểu thức:
\(M = \dfrac{3}{{{{(2x + 1)}^4} + 2}}\)
A. PHẦN TRẮC NGHIỆM
1. C | 2. D | 3. A | 4. A | 5. D | 6. C |
Câu 1
Phương pháp
Định nghĩa số hữu tỉ
Cách giải
Số hữu tỉ là các số viết được dưới dạng \(\dfrac{a}{b}\left( {a,b \in Z,b \ne 0} \right)\)
Chọn C.
Câu 2
Phương pháp
Nếu A = B2 thì A = B hoặc A = -B
Cách giải
Ta có:
\(\begin{array}{l} - 8{x^2} + 50 = 0\\ 8{x^2} = 50\\ {x^2} = \dfrac{{50}}{8} = \dfrac{{25}}{4}\\ {x^2} = {\left( { \pm \dfrac{5}{2}} \right)^2}\\ \left[ {\begin{array}{*{20}{c}}{x = \dfrac{5}{2}}\\{x = - \dfrac{5}{2}}\end{array}} \right.\end{array}\)
Vậy \(x = \pm \dfrac{5}{2}\)
Chọn D.
Câu 3
Phương pháp
Đưa các thừa số về dạng lũy thừa có cơ số là số nguyên tố rồi rút gọn
Cách giải
Ta có:
\(\dfrac{{{3^5}{{.4}^3}}}{{{9^2}{{.8}^2}}} = \dfrac{{{3^5}.{{\left( {{2^2}} \right)}^3}}}{{{{\left( {{3^2}} \right)}^2}.{{\left( {{2^3}} \right)}^2}}} = \dfrac{{{3^5}{{.2}^{2.3}}}}{{{3^{2.2}}{{.2}^{3.2}}}} = \dfrac{{{3^5}{{.2}^6}}}{{{3^4}{{.2}^6}}} = 3\)
Chọn A.
Câu 4
Phương pháp
Xác định các góc tạo bởi 1 đường thẳng cắt 2 đường thẳng
Cách giải
2 góc A1 và B3 ở vị trí so le trong
Chọn A.
Câu 5
Phương pháp
Sử dụng tính chất tia phân giác của một góc.
Tổng số đo của 2 góc kề bù là 180 độ
Cách giải
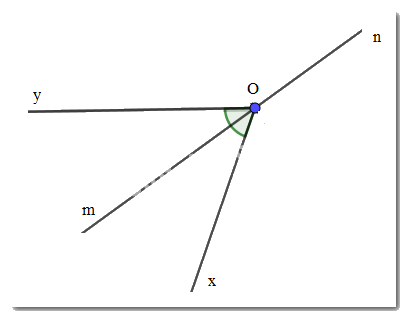
Vì Om là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOm} = \widehat {yOm} = \dfrac{1}{2}.\widehat {xOy} = \dfrac{1}{2}.70^\circ = 35^\circ \)
Mà \(\widehat {xOm},\widehat {xOn}\) là 2 góc kề bù nên \(\widehat {xOm} + \widehat {xOn} = 180^\circ \Rightarrow \widehat {xOn} = 180^\circ - \widehat {xOm} = 180^\circ - 35^\circ = 145^\circ \)
Chọn D.
Câu 6
Phương pháp
Tiên đề Euclid về đường thẳng song song
Cách giải
Theo Tiên đề Euclid về đường thẳng song song: Qua 1 điểm nằm ngoài đường thẳng, có 1 và chỉ 1 đường thẳng song song với đường thẳng đó.
Chọn A.
B. PHẦN TỰ LUẬN
Câu 1
Phương pháp:
a) Sử dụng tính chất phân phối của phép nhân và cộng \(ab + ac = a\left( {b + c} \right)\).
b) Đưa về phân số và tính toán.
Cách giải:
a)
\(\begin{array}{*{20}{l}}{{\mkern 1mu} {\mkern 1mu} \dfrac{4}{{13}}.15\dfrac{3}{{41}} - \dfrac{4}{{13}}.2\dfrac{3}{{41}}}\\{ = \dfrac{4}{{13}}\left( {15\dfrac{3}{{41}} - 2\dfrac{3}{{41}}} \right)}\\{ = \dfrac{4}{{13}}.13}\\{ = 4}\end{array}\)
b)
\(\begin{array}{*{20}{l}}{{\mkern 1mu} {\mkern 1mu} \sqrt {25} .\left( {0,4 - 1\dfrac{1}{2}} \right):\left[ {{{\left( { - 2} \right)}^3}.\dfrac{{11}}{8}} \right]}\\{ = 5.\left( {\dfrac{2}{5} - \dfrac{3}{2}} \right):\left( { - 8.\dfrac{{11}}{8}} \right)}\\{ = 5.\left( {\dfrac{4}{{10}} - \dfrac{{15}}{{10}}} \right):\left( { - 11} \right)}\\{ = 5.\dfrac{{ - 11}}{{10}}.\dfrac{{ - 1}}{{11}}}\\{ = \dfrac{1}{2}}\end{array}\)
Câu 2
Phương pháp
a) Đưa các số hữu tỉ về dạng phân số
Số trừ = số bị trừ - hiệu
b) Đưa 2 tỉ số về dạng có cùng mẫu số rồi sử dụng nhận xét: Nếu \(\dfrac{a}{b} = \dfrac{c}{b} \Rightarrow a = c(b \ne 0)\)
c) Nếu A . B = 0 thì A = 0 hoặc B = 0
Lời giải
a)
\(\begin{array}{l} - 0,12 - 2x = - 1\dfrac{2}{5}\\ \dfrac{{ - 12}}{{100}} - 2x = \dfrac{{ - 7}}{5}\\ \dfrac{{ - 3}}{{25}} - 2x = \dfrac{{ - 7}}{5}\\ 2x = \dfrac{{ - 3}}{{25}} - (\dfrac{{ - 7}}{5})\\ 2x = \dfrac{{ - 3}}{{25}} + \dfrac{{35}}{{25}}\\ 2x = \dfrac{{32}}{{25}}\\ x = \dfrac{{32}}{{25}}:2\\ x = \dfrac{{32}}{{25}}.\dfrac{1}{2}\\ x = \dfrac{{16}}{{25}}\end{array}\)
Vậy \(x = \dfrac{{16}}{{25}}\)
b)
\(\begin{array}{l}\dfrac{{x + \dfrac{3}{2}}}{6} = \dfrac{{ - 5}}{{12}}\\ \dfrac{{2.(x + \dfrac{3}{2})}}{{12}} = \dfrac{{ - 5}}{{12}}\\ \dfrac{{2x + 3}}{{12}} = \dfrac{{ - 5}}{{12}}\\ 2x + 3 = - 5\\ 2x = - 5 - 3\\ 2x = - 8\\ x = - 4\end{array}\)
Vậy x = -4
c)
\(\left( { - 2x + \dfrac{5}{2}} \right).\left( {{x^2} + 4} \right) = 0\)
+) Trường hợp 1:
\(\begin{array}{*{20}{l}}{ - 2x + \dfrac{5}{2} = 0}\\{ 2x = \dfrac{5}{2}}\\{ x = \dfrac{5}{2}:2}\\{ x = \dfrac{5}{4}}\end{array}\)
+) Trường hợp 2:
x2 + 4 = 0
\( {x^2} = - 4\) ( Vô lí vì x2 \( \ge \)0 với mọi x)
Vậy x = \(\dfrac{5}{4}\)
Câu 3
Phương pháp:
+ Áp dụng tính chất: Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau.
+ Dấu hiệu nhận biết hai đường thẳng song song.
Cách giải:
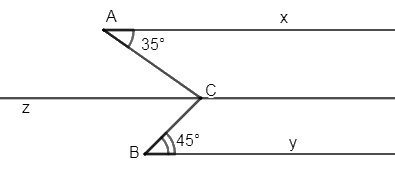
Kẻ \(Cz//{\rm{Ax}} \Rightarrow \widehat {xAC} = \widehat {ACz} = {35^0}\) (so le trong)
Ta có:
\(\widehat {ACz} + \widehat {zCB} = \widehat {ACB} \Rightarrow \widehat {zCB} = \widehat {ACB} - \widehat {ACz} = {80^0} - {35^0} = {45^0}\)
\( \Rightarrow \widehat {zCB} = \widehat {CBy}\left( { = {{45}^0}} \right)\)
Mà hai góc ở vị trí so le trong nên suy ra \(Cz//{\mkern 1mu} By\) (dấu hiệu nhận biết hai đường thẳng song song)
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{Cz//{\mkern 1mu} Ax\left( {gt} \right)}\\{C{\rm{z}}//{\mkern 1mu} By\left( {cmt} \right)}\end{array}} \right. \Rightarrow Ax//{\mkern 1mu} By\) .
Câu 4
Phương pháp
Xét hình tròn bán kính R:
Diện tích hình tròn = 3,14 . R2 , suy ra R
Chu vi hình tròn = 3,14 . R
Cách giải
Ta có: S = 3.14 . R2 hay 200 = 3,14. R2 . Do đó, \({R^2} = \dfrac{{200}}{{3,14}} \approx 63,7 \Rightarrow R = \sqrt {63,7} \approx 7,98(m)\)
Chu vi hình tròn đó là: C = 3,14 . R \( \approx \) 3,14 . 7,98 \( \approx \) 25,0572 (m)
Làm tròn 25,0572 với độ chính xác 0,05, tức là làm tròn đến chữ số thập phân thứ nhất.
Vì chữ số hàng làm tròn là 0, chữ số ngay sau hàng làm tròn là 5 nên ta cộng thêm 1 đơn vị vào chữ số hàng làm tròn, đồng thời bỏ đi các chữ số ở sau hàng làm tròn.
Ta được kết quả chu vi sân đấu làm tròn là 25,1 (m)
Câu 5
Phương pháp
Áp dụng tính chất hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
- Tính chất hai đường thẳng song song.
Cách giải
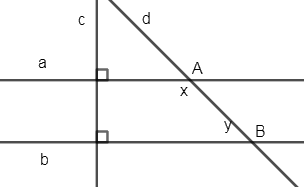
Vì \(a \bot c,{\mkern 1mu} b \bot c\left( {gt} \right) \Rightarrow a//{\mkern 1mu} b \Rightarrow \widehat {aAB} + \widehat {ABb} = {180^0} \Rightarrow x + y = {180^0}\)(2 góc trong cùng phía bù nhau)
\( \Rightarrow x = {180^0} - y\)
Lại có:
\(\begin{array}{*{20}{l}}{2{\rm{x}} = 3y\left( {gt} \right) \Rightarrow 2\left( {{{180}^0} - y} \right) = 3y}\\{ {{360}^0} - 2y = 3y}\\{ 5y = {{360}^0} \Rightarrow y = {{360}^0}:5 = {{72}^0}}\\{ \Rightarrow x = {{180}^0} - {{72}^0} = {{108}^0}}\end{array}\)
Câu 6
Phương pháp:
Đánh giá giá trị của tử và mẫu
Chú ý: a4 \( \ge \) 0, với mọi a
Cách giải:
Vì (2x+1)4 \( \ge \) 0, với mọi x nên (2x+1)4 +2 \( \ge \) 2, với mọi x
\( \Rightarrow \dfrac{3}{{{{(2x + 1)}^4} + 2}} \le \dfrac{3}{2}\), với mọi x. Dấu “=” xảy ra khi 2x + 1 = 0 hay x = \(\dfrac{{ - 1}}{2}\)
Vậy Max M = \(\dfrac{3}{2}\).
Đề thi giữa kì 1 Toán 7 - Đề số 2 chương trình Kết nối tri thức là một bài kiểm tra quan trọng giúp học sinh đánh giá mức độ nắm vững kiến thức đã học trong giai đoạn đầu của năm học lớp 7. Đề thi bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính như số hữu tỉ, số thực, biểu thức đại số, phương trình bậc nhất một ẩn, và các bài toán về hình học cơ bản.
Thông thường, đề thi giữa kì 1 Toán 7 - Đề số 2 - Kết nối tri thức sẽ có cấu trúc gồm các phần sau:
Tỷ lệ điểm giữa phần trắc nghiệm và phần tự luận có thể khác nhau tùy theo quy định của từng trường.
Phần này thường tập trung vào các khái niệm cơ bản về số hữu tỉ, số thực, cách biểu diễn số hữu tỉ, so sánh số hữu tỉ, và các phép toán trên số hữu tỉ. Học sinh cần nắm vững các quy tắc cộng, trừ, nhân, chia số hữu tỉ và áp dụng chúng vào giải các bài toán cụ thể.
Học sinh cần hiểu rõ khái niệm biểu thức đại số, các quy tắc biến đổi biểu thức đại số, và cách thu gọn biểu thức đại số. Các bài tập thường yêu cầu học sinh thu gọn biểu thức, tính giá trị của biểu thức tại một giá trị cụ thể của biến.
Phần này tập trung vào việc giải phương trình bậc nhất một ẩn. Học sinh cần nắm vững các bước giải phương trình, các quy tắc biến đổi tương đương, và cách kiểm tra nghiệm của phương trình.
Các bài toán hình học thường liên quan đến các khái niệm cơ bản về góc, đường thẳng, đoạn thẳng, tam giác, và các tính chất của chúng. Học sinh cần biết cách vẽ hình, sử dụng các công cụ hình học, và áp dụng các định lý, tính chất đã học để giải các bài toán.
Để đạt kết quả tốt trong kỳ thi giữa kì 1 Toán 7 - Đề số 2 - Kết nối tri thức, học sinh cần:
Giaitoan.edu.vn cung cấp đầy đủ các tài liệu ôn thi và luyện tập cho học sinh lớp 7, bao gồm:
Hãy dành thời gian ôn tập và luyện tập một cách nghiêm túc để đạt kết quả tốt nhất trong kỳ thi giữa kì 1 Toán 7 - Đề số 2 - Kết nối tri thức. Chúc các em học sinh thành công!