Chào mừng các em học sinh lớp 7 đến với đề thi học kì 1 môn Toán chương trình Kết nối tri thức - Đề số 17. Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong học kì.
Giaitoan.edu.vn cung cấp đề thi với cấu trúc tương tự đề thi chính thức, giúp các em làm quen với dạng bài và rèn luyện kỹ năng giải quyết vấn đề.
Chọn khẳng định đúng:
\( - 7 \in \mathbb{N}\).
\(\frac{2}{3} \in \mathbb{Z}\).
\(\frac{{ - 2}}{9} \notin \mathbb{Q}\).
\(\frac{1}{{10}} \in \mathbb{Q}\).
Viết gọn tích \({\left( {\frac{1}{3}} \right)^3}.{\left( {\frac{1}{3}} \right)^5}\) ta được:
\({\left( {\frac{1}{3}} \right)^{15}}\).
\({\left( {\frac{1}{3}} \right)^8}\).
\({\left( {\frac{1}{3}} \right)^2}\).
\({\left( {\frac{1}{3}} \right)^7}\).
Cho \(x = 6,67291\). Giá trị của \(x\) khi làm tròn đến chữ số thập phân thứ hai là:
6,673.
6,672.
6,67.
6,6729.
Qua một điểm nằm ngoài một đường thẳng ta có thể kẻ được mấy đường thẳng song song với đường thẳng đó.
0.
1.
2.
vô số.
Nếu \(\sqrt x = 3\) thì \(x\) bằng
6.
12.
-9.
9.
Câu nào dưới đây là đúng:
Nếu \(\left| x \right| = 3,9\) thì \(x = 3,9\).
Nếu \(\left| { - x} \right| = 3,9\) thì \(x = - 3,9\).
Nếu \(x = - 3,9\) thì \(\left| x \right| = 3,9\).
Nếu \( - x = 3,9\) thì \(\left| { - x} \right| = - 3,9\).
Cho hình bên, đường thẳng a song song với b nếu

\(\widehat {{A_4}} = \widehat {{B_1}}\).
\(\widehat {{A_2}} = \widehat {{B_1}}\).
\(\widehat {{A_1}} = \widehat {{B_1}}\).
\(\widehat {{A_4}} = \widehat {{B_3}}\).
Cho \(\widehat {xOy} = 76^\circ \), tia Oz là tia phân giác của \(\widehat {xOy}\). Số đo của \(\widehat {yOz}\) là:
\(33^\circ \).
\(152^\circ \).
\(38^\circ \).
\(42^\circ \).
Cho \(\Delta ABC\) có \(\widehat A = 60^\circ ,\widehat B = 55^\circ \). Số đo của \(\widehat C\) là:
\(55^\circ \).
\(65^\circ \).
\(45^\circ \).
\(75^\circ \).
Chọn câu sai trong các câu sau:
\( - \frac{{11}}{4} < 0\).
\(2\frac{1}{2} > \frac{3}{2}\).
\(0,45 > 0,5\).
\(\frac{3}{4} = 0,75\).
Cho \(\Delta MNP = \Delta DHK\), khẳng định nào sau đây là đúng:
NP = KD.
MP = HK.
MN = DH.
\(\widehat {MPN} = \widehat {DHK}\).
Cho biểu đồ sau:
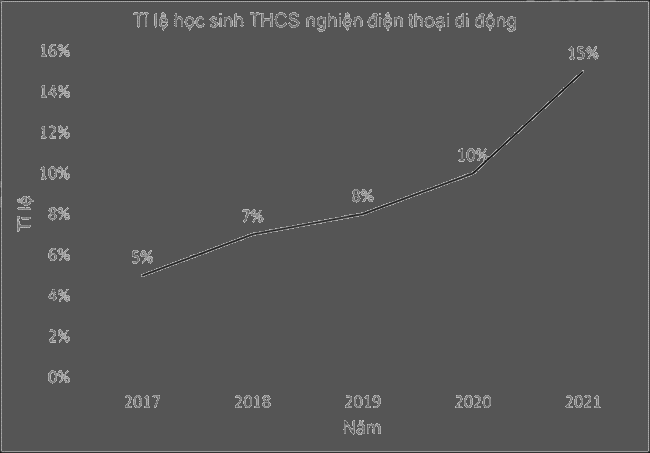
Năm nào có tỉ lệ học sinh THCS nghiện điện thoại cao nhất?
2018.
2019.
2020.
2021.
Thực hiện phép tính:
a) \(\frac{{11}}{{24}} + \frac{{ - 5}}{{41}} + \frac{{13}}{{24}} + \frac{{ - 36}}{{41}} + \frac{1}{2}\)
b) \(\frac{2}{5} + \frac{3}{5}.\frac{7}{6} - \sqrt {\frac{{16}}{{25}}} \)
c) \(\frac{4}{5}.1\frac{2}{9} - \frac{4}{5}.\frac{2}{9} + \frac{3}{5}\)
Tìm \(x\):
a) \(x - \frac{1}{4} = \frac{2}{3}\)
b) \(\frac{1}{4} + \frac{3}{4}x = \frac{{ - 13}}{8}\)
c) \(\left| {\frac{3}{4}x - \frac{1}{2}} \right| + {\left( {\frac{{ - 1}}{2}} \right)^2} = \sqrt {\frac{4}{9}} \)
Cho biểu đồ:
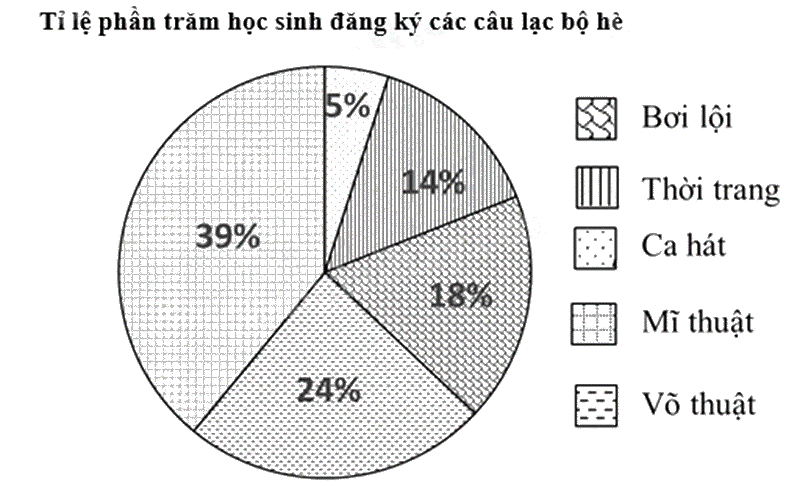
a) Câu lạc bộ nào được học sinh yêu thích nhất khi đăng ký?
b) Em hãy lập bảng thống kê tỉ lệ phần trăm số học sinh đăng ký các câu lạc bộ hè của trường THCS đó.
c) Biết trường THCS đó có 500 học sinh đăng ký các câu lạc bộ hè. Hãy tính số học sinh đăng ký câu lạc bộ bơi lội?
Cho \(\Delta ABC\) có AB = AC. Gọi I là trung điểm của BC.
a) Chứng minh \(\Delta ABI = \Delta ACI\) và \(AI \bot BC\).
b) Trên tia đối của tia IA lấy điểm K sao cho IA = IK. Chứng minh AB = KC.
c) Kẻ \(IE \bot AB\left( {E \in AB} \right)\), \(IF \bot KC\left( {F \in KC} \right)\). Chứng minh E, I, F thẳng hàng.
Chứng tỏ biểu thức sau không phải số nguyên.
\(S = \frac{3}{4} + \frac{8}{9} + \frac{{15}}{{16}} + ... + \frac{{{n^2} - 1}}{{{n^2}}}\left( {n \in \mathbb{N},n > 1} \right)\)
Chọn khẳng định đúng:
\( - 7 \in \mathbb{N}\).
\(\frac{2}{3} \in \mathbb{Z}\).
\(\frac{{ - 2}}{9} \notin \mathbb{Q}\).
\(\frac{1}{{10}} \in \mathbb{Q}\).
Đáp án : D
Kiểm tra xem các số có thuộc tập hợp số đó hay không.
\(\mathbb{N}\) là tập hợp số tự nhiên.
\(\mathbb{Z}\) là tập hợp số nguyên.
\(\mathbb{Q}\) là tập hợp số hữu tỉ.
\( - 7\) không phải là số tự nhiên nên \( - 7 \in \mathbb{N}\) là sai.
\(\frac{2}{3}\) không phải là số nguyên nên \(\frac{2}{3} \in \mathbb{Z}\) là sai.
\(\frac{{ - 2}}{9}\) là số hữu tỉ nên \(\frac{{ - 2}}{9} \notin \mathbb{Q}\) là sai.
\(\frac{1}{{10}}\) là số hữu tỉ nên \(\frac{1}{{10}} \in \mathbb{Q}\) là đúng.
Đáp án D
Viết gọn tích \({\left( {\frac{1}{3}} \right)^3}.{\left( {\frac{1}{3}} \right)^5}\) ta được:
\({\left( {\frac{1}{3}} \right)^{15}}\).
\({\left( {\frac{1}{3}} \right)^8}\).
\({\left( {\frac{1}{3}} \right)^2}\).
\({\left( {\frac{1}{3}} \right)^7}\).
Đáp án : B
Sử dụng kiến thức về tích hai lũy thừa cùng cơ số: \({a^m}.{a^n} = {a^{m + n}}\).
Ta có: \({\left( {\frac{1}{3}} \right)^3}.{\left( {\frac{1}{3}} \right)^5} = {\left( {\frac{1}{3}} \right)^{3 + 5}} = {\left( {\frac{1}{3}} \right)^8}\).
Đáp án B
Cho \(x = 6,67291\). Giá trị của \(x\) khi làm tròn đến chữ số thập phân thứ hai là:
6,673.
6,672.
6,67.
6,6729.
Đáp án : C
Áp dụng quy tắc Làm tròn số thập phân dương:
- Đối với chữ số hàng làm tròn:
+ Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn 5;
+ Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hoặc bằng 5.
- Đối với chữ số sau hàng làm tròn:
+ Bỏ đi nếu ở phần thập phân;
+ Thay bằng các chữ số 0 nếu ở phần số nguyên.
Số \(x = 6,67291\) khi làm tròn đến chữ số thập phân thứ hai là 6,67 (vì số 2 < 5).
Đáp án C
Qua một điểm nằm ngoài một đường thẳng ta có thể kẻ được mấy đường thẳng song song với đường thẳng đó.
0.
1.
2.
vô số.
Đáp án : B
Áp dụng tiên đề Euclid về đường thẳng song song.
Qua một điểm nằm ngoài một đường thẳng, ta chỉ có thể kẻ được 1 đường thẳng song song với đường đó.
Đáp án B
Nếu \(\sqrt x = 3\) thì \(x\) bằng
6.
12.
-9.
9.
Đáp án : D
Áp dụng kiến thức về căn bậc hai của một số: \(\sqrt x = a\) thì \(x = {a^2}\).
Nếu \(\sqrt x = 3\) thì \(x = {3^2} = 9\).
Đáp án D
Câu nào dưới đây là đúng:
Nếu \(\left| x \right| = 3,9\) thì \(x = 3,9\).
Nếu \(\left| { - x} \right| = 3,9\) thì \(x = - 3,9\).
Nếu \(x = - 3,9\) thì \(\left| x \right| = 3,9\).
Nếu \( - x = 3,9\) thì \(\left| { - x} \right| = - 3,9\).
Đáp án : C
Sử dụng kiến thức về giá trị tuyệt đối của một số:
+ Giá trị tuyệt đối của một số dương là chính nó
+ Giá trị tuyệt đối của một số âm là số đối của nó
Nếu |x| = 3,9 thì x = 3,9 hoặc -3,9 nên đáp án A sai (chưa đủ kết quả của x).
Nếu \(\left| { - x} \right| = 3,9\) thì \(x = - 3,9\) thì x = 3,9 hoặc -3,9 đều thỏa mãn nên B sai (chưa đủ kết quả của x).
Nếu \(x = - 3,9\) thì \(\left| x \right| = \left| { - 3,9} \right| = 3,9\) nên C đúng.
Nếu \( - x = 3,9\) thì \(x = - 3,9\) nên \(\left| { - x} \right| = \left| { - \left( { - 3,9} \right)} \right| = \left| {3,9} \right| = 3,9\) nên D sai
Đáp án C
Cho hình bên, đường thẳng a song song với b nếu
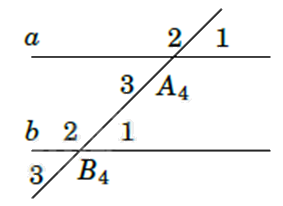
\(\widehat {{A_4}} = \widehat {{B_1}}\).
\(\widehat {{A_2}} = \widehat {{B_1}}\).
\(\widehat {{A_1}} = \widehat {{B_1}}\).
\(\widehat {{A_4}} = \widehat {{B_3}}\).
Đáp án : C
Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau hoặc một cặp góc đồng vị bằng nhau thì a và b song song với nhau.
Quan sát hình vẽ, ta thấy hai góc \(\widehat {{A_1}}\) và \(\widehat {{B_1}}\) ở vị trí đồng vị nên nếu \(\widehat {{A_1}} = \widehat {{B_1}}\) thì đường thẳng a song song với b.
Đáp án C
Cho \(\widehat {xOy} = 76^\circ \), tia Oz là tia phân giác của \(\widehat {xOy}\). Số đo của \(\widehat {yOz}\) là:
\(33^\circ \).
\(152^\circ \).
\(38^\circ \).
\(42^\circ \).
Đáp án : C
Sử dụng tính chất của tia phân giác: tia phân giác chia một góc thành hai góc bằng nhau và bằng một nửa góc đó.
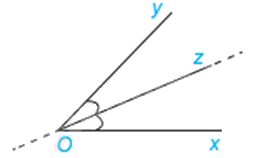
Oz là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {yOz} = \frac{1}{2}\widehat {xOy} = \frac{1}{2}.76^\circ = 38^\circ \).
Đáp án C
Cho \(\Delta ABC\) có \(\widehat A = 60^\circ ,\widehat B = 55^\circ \). Số đo của \(\widehat C\) là:
\(55^\circ \).
\(65^\circ \).
\(45^\circ \).
\(75^\circ \).
Đáp án : B
Áp dụng định lí tổng ba góc của một tam giác bằng \(180^\circ \).
Tam giác ABC có:
\(\widehat A + \widehat B + \widehat C = 180^\circ \) suy ra \(\widehat C = 180^\circ - \widehat A - \widehat B = 180^\circ - 60^\circ - 55^\circ = 65^\circ \).
Đáp án B
Chọn câu sai trong các câu sau:
\( - \frac{{11}}{4} < 0\).
\(2\frac{1}{2} > \frac{3}{2}\).
\(0,45 > 0,5\).
\(\frac{3}{4} = 0,75\).
Đáp án : C
So sánh số hữu tỉ với nhau.
\(0,45 < 0,5\) suy ra C sai.
Đáp án C
Cho \(\Delta MNP = \Delta DHK\), khẳng định nào sau đây là đúng:
NP = KD.
MP = HK.
MN = DH.
\(\widehat {MPN} = \widehat {DHK}\).
Đáp án : C
Hai tam giác bằng nhau thì các cạnh tương ứng và các góc tương ứng bằng nhau.
\(\Delta MNP = \Delta DHK\) thì \(\widehat M = \widehat D;\widehat N = \widehat H;\widehat P = \widehat K\) và \(MN = DH;MP = DK;NP = HK\).
Vậy ta chọn đáp án C
Đáp án C
Cho biểu đồ sau:
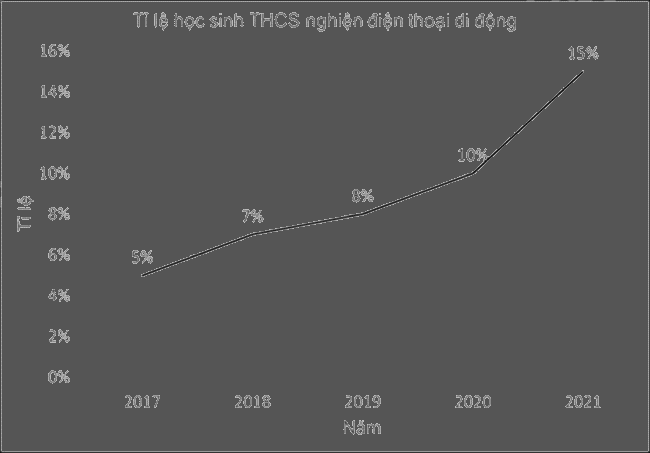
Năm nào có tỉ lệ học sinh THCS nghiện điện thoại cao nhất?
2018.
2019.
2020.
2021.
Đáp án : D
Quan sát xem điểm biểu diễn năm nào lớn nhất thì năm đó có tỉ lệ học sinh THCS nghiện điện thoại cao nhất.
Ta thấy năm 2021 có tỉ lệ lớn nhất (15%) nên tỉ lệ học sinh THCS nghiện điện thoại năm 2021 cao nhất
Đáp án D
Thực hiện phép tính:
a) \(\frac{{11}}{{24}} + \frac{{ - 5}}{{41}} + \frac{{13}}{{24}} + \frac{{ - 36}}{{41}} + \frac{1}{2}\)
b) \(\frac{2}{5} + \frac{3}{5}.\frac{7}{6} - \sqrt {\frac{{16}}{{25}}} \)
c) \(\frac{4}{5}.1\frac{2}{9} - \frac{4}{5}.\frac{2}{9} + \frac{3}{5}\)
a) Sử dụng tính chất kết hợp để đưa các số thành các nhóm.
b) Thực hiện phép tính với số hữu tỉ và căn bậc hai của một số hữu tỉ.
c) Sử dụng tính chất phân phối của phép nhân với phép trừ.
a) \(\frac{{11}}{{24}} + \frac{{ - 5}}{{41}} + \frac{{13}}{{24}} + \frac{{ - 36}}{{41}} + \frac{1}{2}\)
\(\begin{array}{l} = \left( {\frac{{11}}{{24}} + \frac{{13}}{{24}}} \right) + \left( {\frac{{ - 5}}{{41}} + \frac{{ - 36}}{{41}}} \right) + \frac{1}{2}\\ = \frac{{24}}{{24}} + \frac{{ - 41}}{{41}} + \frac{1}{2}\\ = 1 - 1 + \frac{1}{2} = \frac{1}{2}\end{array}\)
b) \(\frac{2}{5} + \frac{3}{5}.\frac{7}{6} - \sqrt {\frac{{16}}{{25}}} \)
\(\begin{array}{l} = \frac{2}{5} + \frac{3}{5}.\frac{7}{6} - \frac{4}{5}\\ = \frac{2}{5} + \frac{7}{{10}} - \frac{4}{5}\\ = \frac{{2.2 + 7 - 4.2}}{{10}}\\ = \frac{3}{{10}}\end{array}\)
c) \(\frac{4}{5}.1\frac{2}{9} - \frac{4}{5}.\frac{2}{9} + \frac{3}{5}\)
\(\begin{array}{l} = \frac{4}{5}.\left( {1\frac{2}{9} - \frac{2}{9}} \right) + \frac{3}{5}\\ = \frac{4}{5}.1 + \frac{3}{5}\\ = \frac{4}{5} + \frac{3}{5} = \frac{7}{5}\end{array}\)
Tìm \(x\):
a) \(x - \frac{1}{4} = \frac{2}{3}\)
b) \(\frac{1}{4} + \frac{3}{4}x = \frac{{ - 13}}{8}\)
c) \(\left| {\frac{3}{4}x - \frac{1}{2}} \right| + {\left( {\frac{{ - 1}}{2}} \right)^2} = \sqrt {\frac{4}{9}} \)
Áp dụng quy tắc chuyển vế đổi dấu.
c) Đưa về dạng \(\left| A \right| = B\), chia hai trường hợp: A = B hoặc A = -B.
a) \(x - \frac{1}{4} = \frac{2}{3}\)
\(\begin{array}{l}x = \frac{2}{3} + \frac{1}{4}\\x = \frac{{11}}{{12}}\end{array}\)
Vậy \(x = \frac{{11}}{{12}}\)
b) \(\frac{1}{4} + \frac{3}{4}x = \frac{{ - 13}}{8}\)
\(\begin{array}{l}\frac{3}{4}x = \frac{{ - 13}}{8} - \frac{1}{4}\\\frac{3}{4}x = \frac{{ - 15}}{8}\\x = \frac{{ - 15}}{8}:\frac{3}{4}\\x = \frac{{ - 5}}{2}\end{array}\)
Vậy \(x = \frac{{ - 5}}{2}\)
c) \(\left| {\frac{3}{4}x - \frac{1}{2}} \right| + {\left( {\frac{{ - 1}}{2}} \right)^2} = \sqrt {\frac{4}{9}} \)
\(\begin{array}{l}\left| {\frac{3}{4}x - \frac{1}{2}} \right| + \frac{1}{4} = \frac{2}{3}\\\left| {\frac{3}{4}x - \frac{1}{2}} \right| = \frac{2}{3} - \frac{1}{4}\\\left| {\frac{3}{4}x - \frac{1}{2}} \right| = \frac{5}{{12}}\\\frac{3}{4}x - \frac{1}{2} = \pm \frac{5}{{12}}\end{array}\)
TH1: \(\frac{3}{4}x - \frac{1}{2} = \frac{5}{{12}}\)
\(\begin{array}{l}\frac{3}{4}x = \frac{5}{{12}} + \frac{1}{2}\\\frac{3}{4}x = \frac{{11}}{{12}}\\x = \frac{{11}}{{12}}:\frac{3}{4}\\x = \frac{{11}}{9}\end{array}\)
TH2: \(\frac{3}{4}x - \frac{1}{2} = - \frac{5}{{12}}\)
\(\begin{array}{l}\frac{3}{4}x = - \frac{5}{{12}} + \frac{1}{2}\\\frac{3}{4}x = \frac{1}{{12}}\\x = \frac{1}{{12}}:\frac{3}{4}\\x = \frac{1}{9}\end{array}\)
Vậy \(x \in \left\{ {\frac{{11}}{9};\frac{1}{9}} \right\}\)
Cho biểu đồ:
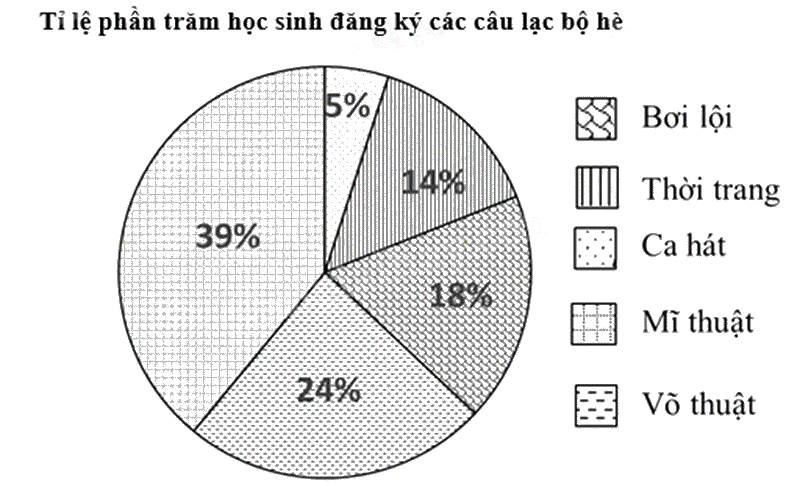
a) Câu lạc bộ nào được học sinh yêu thích nhất khi đăng ký?
b) Em hãy lập bảng thống kê tỉ lệ phần trăm số học sinh đăng ký các câu lạc bộ hè của trường THCS đó.
c) Biết trường THCS đó có 500 học sinh đăng ký các câu lạc bộ hè. Hãy tính số học sinh đăng ký câu lạc bộ bơi lội?
a) Quan sát biểu đồ, câu lạc bộ được yêu thích nhất có tỉ lệ phần trăm học sinh đăng ký nhiều nhất.
b) Từ số liệu trong biểu đồ để lập bảng thống kê.
c) Tính giá trị phần trăm m% của một số a cho trước theo công thức: \(m\% .a\).
a) Câu lạc bộ được học sinh yêu thích nhất khi đăng ký là Mĩ thuật (39%).
b) Bảng thống kê:

c) Số học sinh đăng ký câu lạc bộ bơi lội là: \(18\% .500 = 90\) (học sinh)
Cho \(\Delta ABC\) có AB = AC. Gọi I là trung điểm của BC.
a) Chứng minh \(\Delta ABI = \Delta ACI\) và \(AI \bot BC\).
b) Trên tia đối của tia IA lấy điểm K sao cho IA = IK. Chứng minh AB = KC.
c) Kẻ \(IE \bot AB\left( {E \in AB} \right)\), \(IF \bot KC\left( {F \in KC} \right)\). Chứng minh E, I, F thẳng hàng.
a) Chứng minh \(\Delta ABI = \Delta ACI\) theo trường hợp cạnh – cạnh – cạnh.
Suy ra \(\widehat {AIB} = \widehat {AIC}\).
Mà hai góc này kề bù nên suy ra \(\widehat {AIB} = 90^\circ \) hay \(AI \bot BC\).
b) Chứng minh \(\Delta ABI = \Delta KCI\) suy ra AB = KC.
c) Chứng minh \(\Delta BIE = \Delta CIF\) suy ra \(\widehat {BIE} = \widehat {CIF}\). Sử dụng tính chất hai góc kề bù suy ra \(\widehat {EIF} = 180^\circ \) nên E, I, F thẳng hàng.
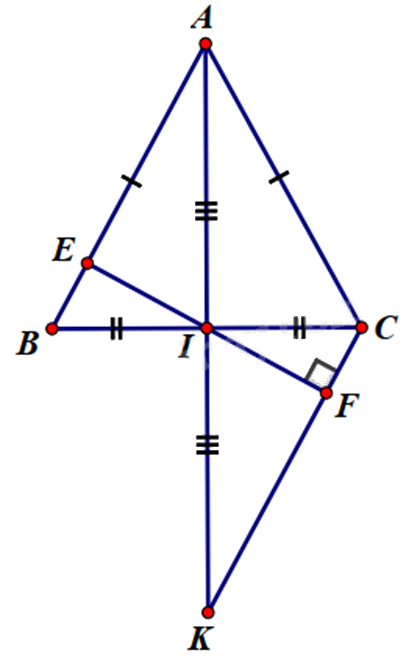
a) Xét \(\Delta ABI\) và \(\Delta ACI\) có:
\(AB = AC\) (gt)
\(BI = CI\) (I là trung điểm của BC)
\(AI\) chung
Suy ra \(\Delta ABI = \Delta ACI\) (c.c.c)
Suy ra \(\widehat {AIB} = \widehat {AIC}\).
Mà hai góc này kề bù nên \(\widehat {AIB} + \widehat {AIC} = 180^\circ \), suy ra \(\widehat {AIB} = \widehat {AIC} = \frac{{180^\circ }}{2} = 90^\circ \) hay \(AI \bot BC\).
b) Xét \(\Delta ABI\) và \(\Delta KCI\) có:
\(AI = KI\) (gt)
\(\widehat {AIB} = \widehat {KIC}\left( { = 90^\circ } \right)\)
\(BI = CI\)
Suy ra \(\Delta ABI = \Delta KCI\) (c.g.c) suy ra AB = KC.
c) Vì \(\Delta ABI = \Delta KCI\) nên \(\widehat {ABI} = \widehat {KCI}\)
Xét \(\Delta BIE\) và \(\Delta CIF\) ta có:
\(\widehat {BEI} = \widehat {CFI}\left( { = 90^\circ } \right)\)
\(\widehat {EBI} = \widehat {FCI}\)
\(BI = CI\)
Suy ra \(\Delta BIE = \Delta CIF\) (cạnh huyền – góc nhọn)
Do đó \(\widehat {BIE} = \widehat {CIF}\).
Mà \(\widehat {BIE}\) và \(\widehat {EIC}\) là hai góc kề bù nên \(\widehat {BIE} + \widehat {EIC} = 180^\circ \)
nên \(\widehat {EIC} + \widehat {CIF} = 180^\circ \) hay \(\widehat {EIF} = 180^\circ \) nên E, I, F thẳng hàng.
Chứng tỏ biểu thức sau không phải số nguyên.
\(S = \frac{3}{4} + \frac{8}{9} + \frac{{15}}{{16}} + ... + \frac{{{n^2} - 1}}{{{n^2}}}\left( {n \in \mathbb{N},n > 1} \right)\)
Biến đổi các phân số thành \(\frac{{{n^2} - 1}}{{{n^2}}}\) để rút gọn S.
Chứng minh \(n - 2 < S < n - 1\) nên S không là số nguyên.
Ta có:
\(\begin{array}{l}S = \frac{3}{4} + \frac{8}{9} + \frac{{15}}{{16}} + ... + \frac{{{n^2} - 1}}{{{n^2}}}\\ = \frac{{{2^2} - 1}}{{{2^2}}} + \frac{{{3^2} - 1}}{{{3^2}}} + \frac{{{4^2} - 1}}{{{4^2}}} + ... + \frac{{{n^2} - 1}}{{{n^2}}}\\ = 1 - \frac{1}{{{2^2}}} + 1 - \frac{1}{{{3^2}}} + 1 - \frac{1}{{{4^2}}} + ...1 + \frac{1}{{{n^2}}}\\ = \left( {1 + 1 + ... + 1} \right) - \left( {\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{n^2}}}} \right)\\ = \left( {n - 1} \right) - \left( {\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{n^2}}}} \right)\end{array}\)
+) Vì \(\left( {\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{n^2}}}} \right) > 0\) nên \(S < n - 1\) (1)
+) \(\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{n^2}}} < \frac{1}{{1.2}} + \frac{1}{{2.3}} + \frac{1}{{3.4}} + ... + \frac{1}{{\left( {n - 1} \right).n}} = 1 - \frac{1}{n} < 1\)
Suy ra \( - \left( {\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{n^2}}}} \right) > - 1\)
Suy ra \(\left( {n - 1} \right) - \left( {\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{n^2}}}} \right) > \left( {n - 1} \right) - 1 = n - 2\)
Do đó \(S > n - 2\) (2)
Từ (1) và (2) suy ra \(n - 2 < S < n - 1\)
Vì giữa n – 2 và n – 1 không có số nguyên nào nên S không là số nguyên.
Đề thi học kì 1 Toán 7 Kết nối tri thức - Đề số 17 là một bài kiểm tra quan trọng đánh giá mức độ nắm vững kiến thức và kỹ năng của học sinh sau nửa học kỳ đầu tiên. Đề thi bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính như số hữu tỉ, số thực, biểu thức đại số, phương trình bậc nhất một ẩn, bất đẳng thức và các ứng dụng thực tế của toán học.
Đề thi thường được chia thành các phần sau:
Phần trắc nghiệm thường bao gồm các câu hỏi liên quan đến:
Phần tự luận thường bao gồm các bài toán sau:
Ví dụ 1: Giải phương trình 2x + 5 = 11
Lời giải:
2x + 5 = 11
2x = 11 - 5
2x = 6
x = 3
Ví dụ 2: Tìm giá trị nhỏ nhất của biểu thức A = (x - 2)^2 + 3
Lời giải:
Vì (x - 2)^2 ≥ 0 với mọi x, nên A = (x - 2)^2 + 3 ≥ 3 với mọi x.
Dấu bằng xảy ra khi (x - 2)^2 = 0, tức là x = 2.
Vậy giá trị nhỏ nhất của A là 3 khi x = 2.
Để chuẩn bị tốt nhất cho kỳ thi học kì 1, các em có thể tham khảo các tài liệu sau:
Đề thi học kì 1 Toán 7 Kết nối tri thức - Đề số 17 là cơ hội để các em thể hiện những kiến thức và kỹ năng đã học. Hãy tự tin và làm bài một cách tốt nhất nhé!