Chào mừng các em học sinh lớp 7 đến với đề thi giữa kì 1 Toán 7 Kết nối tri thức - Đề số 12. Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong giai đoạn đầu của năm học.
Giaitoan.edu.vn cung cấp đề thi với cấu trúc bám sát chương trình học, giúp các em làm quen với dạng đề và rèn luyện kỹ năng giải toán.
Trong các khẳng định sau, khẳng định nào đúng?
\( - 9 \in \mathbb{N}\).
\(\frac{7}{3} \in \mathbb{Z}\).
\(1,2 \notin \mathbb{R}\).
\(\frac{{ - 5}}{2} \in \mathbb{Q}\).
Trong các số \(\frac{{ - 9}}{5};\frac{{ - 7}}{{ - 15}};0,2; - 3\frac{5}{2};\frac{0}{8};\frac{{13}}{5}\) có bao nhiêu số hữu tỉ dương?
1.
2.
3.
4.
Số đối của \(\frac{{ - 2}}{3}\) là
\(\frac{2}{3}\).
\(\frac{3}{2}\).
\(\frac{{ - 3}}{2}\).
\(\frac{2}{{ - 3}}\).
Giá trị của x thỏa mãn \(\left| x \right| = 3\) là
\(x = 3\).
\(x = - 3\).
\(x = 3\) hoặc \(x = - 3\).
\(x = 9\).
Kết quả của phép tính \({2^2}{.2^5}\) là
\({2^{10}}\).
\({2^3}\).
\({2^5}\).
\({2^7}\).
Căn bậc hai số học của 64 là
32.
8 và -8.
-8.
8.
Trong các số sau, số nào là số vô tỉ?
\(\sqrt {{5^2}} \).
\(\sqrt 3 \).
\(\sqrt {{{\left( {3,5} \right)}^2}} \).
\(\sqrt {16} \).
Làm tròn số \(5,16578\) với độ chính xác \(0,005\)
5,17.
5,2.
5.
5,166.
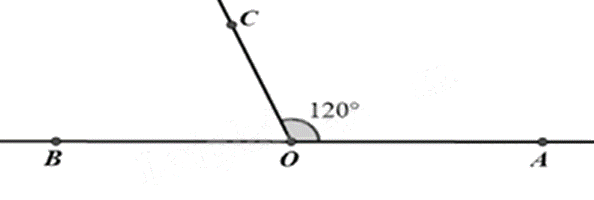
Số đo \(\widehat {BOC}\) trong hình là
\(60^\circ \).
\(120^\circ \).
\(180^\circ \).
\(90^\circ \).
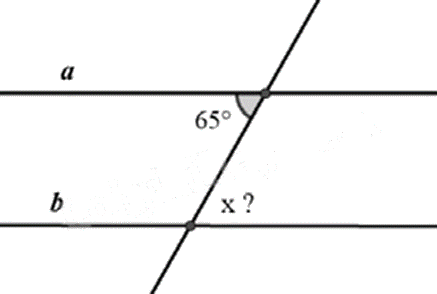
Cho a // b, số đo góc x trên hình vẽ là
\(115^\circ \).
\(90^\circ \).
\(65^\circ \).
\(0^\circ \).
Qua một điểm M nằm ngoài đường thẳng a, kẻ được bao nhiêu đường thẳng song song với đường thẳng a?
Có vô số.
Không có.
Có hai đường thẳng.
Chỉ có một.
Cho ba đường thẳng phân biệt a, b, c biết \(a \bot c\) và \(c \bot b\). Kết luận nào đúng?
a cắt b.
a // b.
\(a \bot b\).
a trùng b.
Thực hiện phép tính (Tính nhanh nếu có thể):
a) \(\frac{9}{8} - \frac{1}{8}:\frac{3}{4}\);
b) \(\frac{{23}}{{25}} - \frac{{19}}{{43}} + \frac{{27}}{{25}} - \frac{{24}}{{43}}\);
c) \(\frac{2}{5}.\frac{{ - 17}}{9} + \frac{2}{5}.\left| {\frac{{ - 8}}{9}} \right| - \sqrt {16} \).
Tìm x, biết:
a) \(x + 4,5 = 9,5\);
b) \(\frac{7}{5}x - \frac{1}{2} = \frac{3}{8}\);
c) \(\left| {3x - 1} \right| + \frac{1}{3} = \frac{1}{2}\)
Khoai tây là thức ăn chính của Châu Âu và là một món ăn ưa thích của người Việt Nam. Trong 100g khoai tây khô có 11g nước; 6,6g protein; 0,3g chất béo; 75,1g glucid và các chất khác. (Theo Viện Dinh dưỡng Quốc gia).
Em hãy cho biết khối lượng các chất khác trong 300g khoai tây khô.
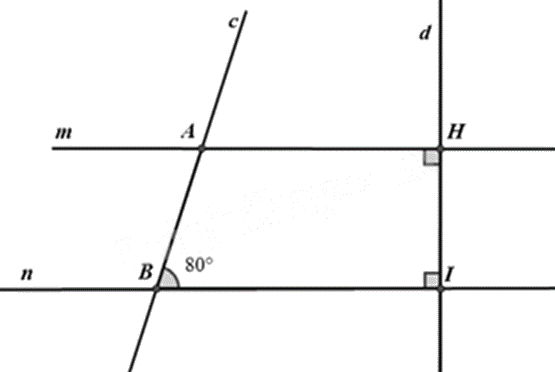
Cho hình vẽ, biết \(\widehat {ABI} = 80^\circ \).
a) Chứng minh \(m//n\).
b) Tính \(\widehat {cAH}\) và \(\widehat {mAc}\).
c) Vẽ tia AE là tia phân giác của \(\widehat {cAH}\). Tia BF là tia phân giác của \(\widehat {ABI}\). Chứng minh \(AE//BF\).
Cho \(M = \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{3^4}}} + \frac{1}{{{3^6}}} + ... + \frac{1}{{{3^{802}}}}\). Chứng minh rằng \(M < \frac{3}{8}\).
Trong các khẳng định sau, khẳng định nào đúng?
\( - 9 \in \mathbb{N}\).
\(\frac{7}{3} \in \mathbb{Z}\).
\(1,2 \notin \mathbb{R}\).
\(\frac{{ - 5}}{2} \in \mathbb{Q}\).
Đáp án : D
Dựa vào kiến thức về các tập hợp \(\mathbb{N},\mathbb{Z},\mathbb{R},\mathbb{Q}\).
\( - 9\) không phải số tự nhiên nên \( - 9 \in \mathbb{N}\) là khẳng định sai.
\(\frac{7}{3}\) không phải số nguyên nên \(\frac{7}{3} \in \mathbb{Z}\) là khẳng định sai.
\(1,2\) là số thực nên khẳng định \(1,2 \notin \mathbb{R}\) là khẳng định sai.
\(\frac{{ - 5}}{2}\) là số hữu tỉ nên \(\frac{{ - 5}}{2} \in \mathbb{Q}\) là khẳng định đúng.
Đáp án D.
Trong các số \(\frac{{ - 9}}{5};\frac{{ - 7}}{{ - 15}};0,2; - 3\frac{5}{2};\frac{0}{8};\frac{{13}}{5}\) có bao nhiêu số hữu tỉ dương?
1.
2.
3.
4.
Đáp án : C
Số hữu tỉ dương là các số viết được dưới dạng phân số và lớn hơn 0.
Có 3 số hữu tỉ dương, đó là: \(\frac{{ - 7}}{{ - 15}};0,2;\frac{{13}}{5}\).
Vì \(\frac{{ - 7}}{{ - 15}} = \frac{7}{{15}}\); \(0,2 = \frac{2}{{10}} = \frac{1}{5}\) và \(\frac{{13}}{5}\) đều là số hữu tỉ.
Đáp án C.
Số đối của \(\frac{{ - 2}}{3}\) là
\(\frac{2}{3}\).
\(\frac{3}{2}\).
\(\frac{{ - 3}}{2}\).
\(\frac{2}{{ - 3}}\).
Đáp án : A
Số đối của số hữu tỉ a là – a.
Số đối của \(\frac{{ - 2}}{3}\) là: \( - \left( {\frac{{ - 2}}{3}} \right) = \frac{2}{3}\).
Đáp án A.
Giá trị của x thỏa mãn \(\left| x \right| = 3\) là
\(x = 3\).
\(x = - 3\).
\(x = 3\) hoặc \(x = - 3\).
\(x = 9\).
Đáp án : C
Khi \(\left| x \right| = k > 0\) thì xảy ra hai trường hợp: \(x = k\) hoặc \(x = - k\).
Ta có: \(\left| x \right| = 3\) nên \(x = 3\) hoặc \(x = - 3\).
Đáp án C.
Kết quả của phép tính \({2^2}{.2^5}\) là
\({2^{10}}\).
\({2^3}\).
\({2^5}\).
\({2^7}\).
Đáp án : D
Khi nhân 2 lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng 2 số mũ:
\({x^m}.{x^n} = {x^{m + n}}\).
Ta có: \({2^2}{.2^5} = {2^{2 + 5}} = {2^7}\).
Đáp án D.
Căn bậc hai số học của 64 là
32.
8 và -8.
-8.
8.
Đáp án : D
Căn bậc hai số học của một số a không âm, kí hiệu \(\sqrt a \), là số x không âm sao cho \({x^2} = a\).
Căn bậc hai số học của 64 là: \(\sqrt {64} = \sqrt {{8^2}} = 8\).
* Lưu ý: -8 không phải là căn bậc hai số học của 64.
Đáp án D.
Trong các số sau, số nào là số vô tỉ?
\(\sqrt {{5^2}} \).
\(\sqrt 3 \).
\(\sqrt {{{\left( {3,5} \right)}^2}} \).
\(\sqrt {16} \).
Đáp án : B
Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn.
\(\sqrt {{5^2}} \) không phải số vô tỉ vì \(\sqrt {{5^2}} = 5\).
\(\sqrt 3 \) là số vô tỉ.
\(\sqrt {{{\left( {3,5} \right)}^2}} \) không phải số vô tỉ vì \(\sqrt {{{\left( {3,5} \right)}^2}} = 3,5\).
\(\sqrt {16} \) không phải số vô tỉ vì \(\sqrt {16} = \sqrt {{4^2}} = 4\).
Đáp án B.
Làm tròn số \(5,16578\) với độ chính xác \(0,005\)
5,17.
5,2.
5.
5,166.
Đáp án : A
Làm tròn số với độ chính xác:
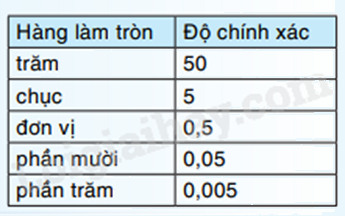
Làm tròn số \(5,16578\) với độ chính xác 0,005, tức là làm tròn số \(5,16578\) đến hàng phần trăm, ta được \(5,17\).
Đáp án A.
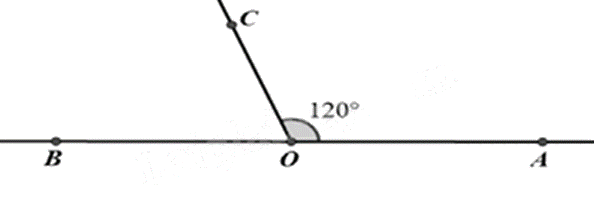
Số đo \(\widehat {BOC}\) trong hình là
\(60^\circ \).
\(120^\circ \).
\(180^\circ \).
\(90^\circ \).
Đáp án : A
Dựa vào kiến thức về hai góc kề bù: Hai góc kề bù có tổng là \(180^\circ \).
Vì \(\widehat {BOC}\) và \(\widehat {COA}\) là hai góc kề bù nên ta có: \(\widehat {BOC} + \widehat {COA} = 180^\circ \).
Suy ra \(\widehat {BOC} = 180^\circ - \widehat {COA} = 180^\circ - 120^\circ = 60^\circ \).
Đáp án A.
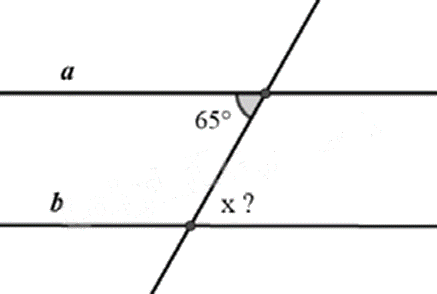
Cho a // b, số đo góc x trên hình vẽ là
\(115^\circ \).
\(90^\circ \).
\(65^\circ \).
\(0^\circ \).
Đáp án : C
Dựa vào kiến thức về tính chất hai đường thẳng song song.
Vì a // b nên \(x = 65^\circ \) (hai góc so le trong).
Đáp án C.
Qua một điểm M nằm ngoài đường thẳng a, kẻ được bao nhiêu đường thẳng song song với đường thẳng a?
Có vô số.
Không có.
Có hai đường thẳng.
Chỉ có một.
Đáp án : D
Áp dụng tiên đề Euclid về đường thẳng song song.
Theo tiên đề Euclid ta có: Qua điểm M ở ngoài đường thẳng a cho trước, vẽ được duy nhất một đường thẳng song song với đường thẳng đó.
Đáp án D.
Cho ba đường thẳng phân biệt a, b, c biết \(a \bot c\) và \(c \bot b\). Kết luận nào đúng?
a cắt b.
a // b.
\(a \bot b\).
a trùng b.
Đáp án : B
Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
Vì \(a \bot c\) và \(c \bot b\) nên a // b.
Đáp án B.
Thực hiện phép tính (Tính nhanh nếu có thể):
a) \(\frac{9}{8} - \frac{1}{8}:\frac{3}{4}\);
b) \(\frac{{23}}{{25}} - \frac{{19}}{{43}} + \frac{{27}}{{25}} - \frac{{24}}{{43}}\);
c) \(\frac{2}{5}.\frac{{ - 17}}{9} + \frac{2}{5}.\left| {\frac{{ - 8}}{9}} \right| - \sqrt {16} \).
Dựa vào quy tắc thực hiện phép tính với số hữu tỉ, giá trị tuyệt đối và căn bậc hai để thực hiện.
a) \(\frac{9}{8} - \frac{1}{8}:\frac{3}{4}\) \( = \frac{9}{8} - \frac{1}{8}.\frac{4}{3}\) \( = \frac{9}{8} - \frac{1}{6}\) \( = \frac{{23}}{{24}}\).
b) \(\frac{{23}}{{25}} - \frac{{19}}{{43}} + \frac{{27}}{{25}} - \frac{{24}}{{43}}\) \( = \left( {\frac{{23}}{{25}} + \frac{{27}}{{25}}} \right) - \left( {\frac{{19}}{{43}} + \frac{{24}}{{43}}} \right)\) \( = 2 - 1\) \( = 1\).
c) \(\frac{2}{5}.\frac{{ - 17}}{9} + \frac{2}{5}.\left| {\frac{{ - 8}}{9}} \right| - \sqrt {16} \) \( = \frac{2}{5}.\frac{{ - 17}}{9} + \frac{2}{5}.\frac{8}{9} - 4\) \( = \frac{2}{5}.\left( {\frac{{ - 17}}{9} + \frac{8}{9}} \right) - 4\) \( = \frac{2}{5}.\left( { - 1} \right) - 4\) \( = \frac{{ - 2}}{5} - 4\) \( = \frac{{ - 22}}{5}\).
Tìm x, biết:
a) \(x + 4,5 = 9,5\);
b) \(\frac{7}{5}x - \frac{1}{2} = \frac{3}{8}\);
c) \(\left| {3x - 1} \right| + \frac{1}{3} = \frac{1}{2}\)
a, b) Sử dụng quy tắc chuyển vế và thực hiện phép tính để tìm x.
c) Chuyển vế, sử dụng kiến thức \(\left| A \right| = k > 0\) thì xảy ra hai trường hợp: \(A = k\) hoặc \(A = - k\).
a) \(x + 4,5 = 9,5\)
\(x = 9,5 - 4,5\)
\(x = 5\)
Vậy \(x = 5\).
b) \(\frac{7}{5}x - \frac{1}{2} = \frac{3}{8}\)
\(\begin{array}{l}\frac{7}{5}x = \frac{3}{8} + \frac{1}{2}\\\frac{7}{5}x = \frac{7}{8}\\x = \frac{7}{8}:\frac{7}{5}\\x = \frac{7}{8}.\frac{5}{7}\\x = \frac{5}{8}\end{array}\)
Vậy \(x = \frac{5}{8}\).
c) \(\left| {3x - 1} \right| + \frac{1}{3} = \frac{1}{2}\)
\(\begin{array}{l}\left| {3x - 1} \right| = \frac{1}{2} - \frac{1}{3}\\\left| {3x - 1} \right| = \frac{1}{6}\end{array}\)
Suy ra \(3x - 1 = \frac{1}{6}\) hoặc \(3x - 1 = \frac{{ - 1}}{6}\)
TH1: \(3x - 1 = \frac{1}{6}\)
\(\begin{array}{l}3x = \frac{1}{6} + 1\\3x = \frac{7}{6}\\x = \frac{7}{6}:3\\x = \frac{7}{{18}}\end{array}\)
TH2: \(3x - 1 = \frac{{ - 1}}{6}\)
\(\begin{array}{l}3x = - \frac{1}{6} + 1\\3x = \frac{5}{6}\\x = \frac{5}{6}:3\\x = \frac{5}{{18}}\end{array}\)
Vậy \(x = \frac{7}{{18}};x = \frac{5}{{18}}\).
Khoai tây là thức ăn chính của Châu Âu và là một món ăn ưa thích của người Việt Nam. Trong 100g khoai tây khô có 11g nước; 6,6g protein; 0,3g chất béo; 75,1g glucid và các chất khác. (Theo Viện Dinh dưỡng Quốc gia).
Em hãy cho biết khối lượng các chất khác trong 300g khoai tây khô.
Áp dụng quy tắc cộng, trừ với số thực.
Khối lượng chất khác trong 100g khoai tây khô là:
\(100 - 11 - 6,6 - 0,3 - 75,1 = 89 - \left( {6,6 + 0,3 + 75,1} \right) = 89 - 82 = 7\left( g \right)\)
Khối lượng chất khác trong 300g khoai tây khô là:
\(7.3 = 21\left( g \right)\)
Vậy khối lượng chất khác trong 300g khoai tây khô là 21g.
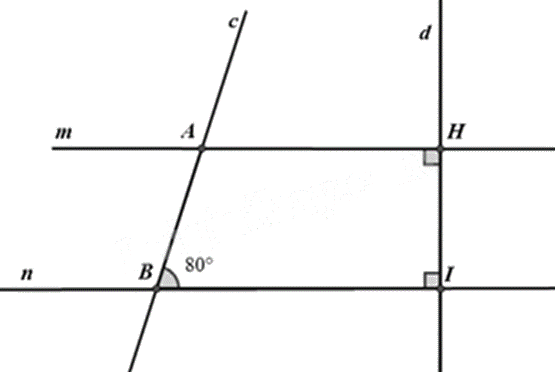
Cho hình vẽ, biết \(\widehat {ABI} = 80^\circ \).
a) Chứng minh \(m//n\).
b) Tính \(\widehat {cAH}\) và \(\widehat {mAc}\).
c) Vẽ tia AE là tia phân giác của \(\widehat {cAH}\). Tia BF là tia phân giác của \(\widehat {ABI}\). Chứng minh \(AE//BF\).
a) Sử dụng dấu hiệu nhận biết hai đường thẳng song song: Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
b) Sử dụng tính chất của hai đường thẳng song song: hai góc đồng vị bằng nhau.
Hai góc kề bù thì tổng của chúng bằng \(180^\circ \).
c) Sử dụng kiến thức về tia phân giác của một góc.
Sử dụng dấu hiệu nhận biết hai đường thẳng song song (hai góc bằng nhau ở vị trí đồng vị)
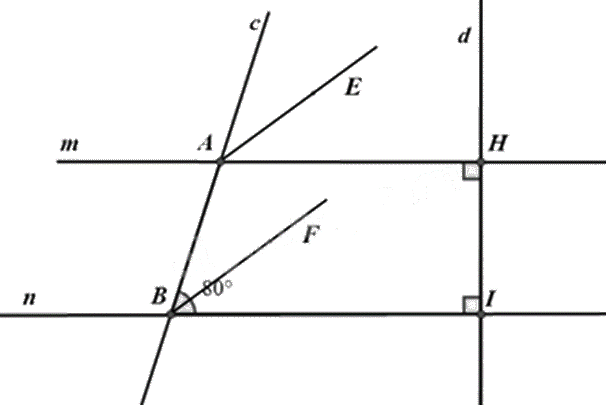
a) Ta có: \(m \bot d;n \bot d\) nên m // n (tính chất hai đường thẳng song song).
b) Vì m // n nên \(\widehat {cAH} = \widehat {ABI} = 80^\circ \) (hai góc đồng vị).
Vì \(\widehat {mAc}\) và \(\widehat {cAH}\) là hai góc kề bù nên ta có \(\widehat {mAc} + \widehat {cAH} = 180^\circ \)
Suy ra \(\widehat {mAc} = 180^\circ - \widehat {cAH} = 180^\circ - 80^\circ = 100^\circ \).
Vậy \(\widehat {cAH} = 80^\circ ;\widehat {mAc} = 100^\circ \).
c) Vì AE là tia phân giác của \(\widehat {cAH}\) nên \(\widehat {cAE} = \frac{1}{2}\widehat {cAH} = \frac{{80^\circ }}{2} = 40^\circ \).
Tương tự, ta tính được \(\widehat {ABF} = 40^\circ \).
Ta có \(\widehat {cAE} = \widehat {ABF} = 40^\circ \).
Mà hai góc này là hai góc ở vị trí đồng vị nên AE // BF.
Cho \(M = \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{3^4}}} + \frac{1}{{{3^6}}} + ... + \frac{1}{{{3^{802}}}}\). Chứng minh rằng \(M < \frac{3}{8}\).
Đặt \(A = \frac{1}{{{3^2}}} + \frac{1}{{{3^4}}} + \frac{1}{{{3^6}}} + ... + \frac{1}{{{3^{802}}}}\)
Nhân hai vế của \(A\) với \({3^2}\).
Lấy \({3^2}A - A\), so sánh với 1 để chứng minh \(A < \frac{1}{8}\).
Từ đó chứng minh \(M = \frac{1}{{{2^2}}} + A < \frac{3}{8}\)
Đặt \(A = \frac{1}{{{3^2}}} + \frac{1}{{{3^4}}} + \frac{1}{{{3^6}}} + ... + \frac{1}{{{3^{802}}}}\)
Ta có: \({3^2}.A = {3^2}.\left( {\frac{1}{{{3^2}}} + \frac{1}{{{3^4}}} + \frac{1}{{{3^6}}} + ... + \frac{1}{{{3^{802}}}}} \right)\)
\(9A = 1 + \frac{1}{{{3^2}}} + \frac{1}{{{3^4}}} + \frac{1}{{{3^6}}} + ... + \frac{1}{{{3^{800}}}}\)
Suy ra
\(9A - A = \left( {1 + \frac{1}{{{3^2}}} + \frac{1}{{{3^4}}} + \frac{1}{{{3^6}}} + ... + \frac{1}{{{3^{800}}}}} \right) - \left( {\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{3^4}}} + \frac{1}{{{3^6}}} + ... + \frac{1}{{{3^{802}}}}} \right)\)
\(8A = 1 - \frac{1}{{{3^{802}}}}\)
Vì \(1 - \frac{1}{{{3^{802}}}} < 1\) nên \(8A < 1\), suy ra \(A < \frac{1}{8}\).
Mà \(M = \frac{1}{{{2^2}}} + A < \frac{1}{4} + \frac{1}{8} = \frac{3}{8}\) nên \(M < \frac{3}{8}\).
Vậy \(M < \frac{3}{8}\).
Đề thi giữa kì 1 Toán 7 Kết nối tri thức - Đề số 12 là một bài kiểm tra quan trọng giúp đánh giá mức độ nắm vững kiến thức của học sinh sau một thời gian học tập. Đề thi bao gồm các dạng bài tập khác nhau, tập trung vào các chủ đề chính được giảng dạy trong chương trình học kì 1. Việc làm quen với cấu trúc đề thi và luyện tập giải các bài tập tương tự là rất quan trọng để đạt kết quả tốt.
Đề thi thường bao gồm các phần sau:
Các chủ đề thường xuất hiện trong đề thi:
Để giải đề thi hiệu quả, học sinh cần:
Bài 1: Tính giá trị của biểu thức sau: (1/2 + 1/3) * 6
Lời giải:
(1/2 + 1/3) * 6 = (3/6 + 2/6) * 6 = (5/6) * 6 = 5
Để nâng cao kỹ năng giải toán, học sinh nên luyện tập thêm với các đề thi khác và các bài tập tương tự. Giaitoan.edu.vn cung cấp một kho đề thi phong phú và đa dạng, đáp ứng nhu cầu ôn luyện của học sinh.
Việc ôn tập thường xuyên và có hệ thống là rất quan trọng để nắm vững kiến thức và đạt kết quả tốt trong các kỳ thi. Học sinh nên dành thời gian ôn tập lại các kiến thức đã học, giải các bài tập và làm các đề thi thử để làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Hãy tự tin vào khả năng của mình và luôn cố gắng hết sức trong quá trình học tập. Đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè nếu gặp khó khăn. Chúc các em học sinh đạt kết quả tốt trong kỳ thi giữa kì 1 Toán 7!
| Chủ đề | Mức độ quan trọng |
|---|---|
| Số hữu tỉ và số thực | Cao |
| Tỉ lệ thức | Trung bình |
| Biểu thức đại số | Trung bình |
| Phương trình bậc nhất một ẩn | Thấp |
| Hình học | Cao |