Chào mừng các em học sinh lớp 7 đến với đề thi học kì 1 môn Toán - Đề số 2, chương trình Kết nối tri thức. Đề thi này được thiết kế để giúp các em ôn luyện và đánh giá kiến thức đã học trong học kì.
Giaitoan.edu.vn cung cấp đề thi chính thức, đáp án chi tiết và lời giải bài tập giúp các em tự tin làm bài và đạt kết quả tốt nhất.
I. TRẮC NGHIỆM ( 3 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I: Trắc nghiệm
1.B | 2.C | 3.D | 4.D | 5.B | 6.D | 7.C | 8.C | 9.A | 10.A |
Câu 1
Phương pháp:
Quy đồng các phân số cùng mẫu dương để so sánh.
Cách giải:
*Ta có: \(11 < 9\), do đó, \(\frac{5}{{11}} < \frac{5}{9}\) suy ra \(\frac{{ - 5}}{{11}} > \frac{{ - 5}}{9}\)
*Ta có: \(\frac{7}{5} = \frac{{91}}{{65}}\,\,;\,\,\frac{3}{5} = \frac{{39}}{{65}}\,\,;\,\,\frac{{18}}{{13}} = \frac{{90}}{{65}}\)
Vì \(39 < 90 < 91\) nên \(\frac{{39}}{{65}} < \frac{{90}}{{65}} < \frac{{91}}{{65}}\) hay \(\frac{3}{5} < \frac{{18}}{{13}} < \frac{7}{5}\)
Thứ tự tăng dần của các số hữu tỉ là: \(\frac{{ - 5}}{{9}}\,\,;\,\,\frac{{ - 5}}{11}\,\,;\,\,\frac{3}{5}\,\,;\,\,\frac{{18}}{{13}}\,\,;\,\,\frac{7}{5}.\)
Chọn B.
Câu 2
Phương pháp:
Vận dụng công thức tính lũy thừa của một thường bằng thương các lũy thừa: \({\left( {\frac{x}{y}} \right)^n} = \frac{{{x^n}}}{{{y^n}}}\,\left( {y \ne 0} \right)\)
Cách giải:
\({\left( {\frac{3}{5}} \right)^{10}}:{5^{10}}\)\( = \frac{{{3^{10}}}}{{{5^{10}}}}{.5^{10}} = {3^{10}}\)
Chọn C.
Câu 3
Phương pháp:
Thực hiện tính căn bậc hai.
Cách giải:
\(\begin{array}{l}\,\,\,\,\sqrt {0,04} + \sqrt {0,25} + 2,31\\ = 0,2 + 0,5 + 2,31\\ = 0,7 + 2,31\\ = 3,01\end{array}\)
Chọn D.
Câu 4
Phương pháp:
Vận dụng kiến thức về dấu giá trị tuyệt đối của một số.
Cách giải:
+ Đáp án A sai, khi \(x < y\)
+ Đáp án B sai, lấy ví dụ khi \(x = 0;y \ne 0\)
+ Đáp án C sai, lấy ví dụ khi \(x = - y \ne 0\)
+ Đáp án D đúng, theo quy tắc cộng hai số trái dấu.
Chọn D.
Câu 5
Phương pháp:
Từ giả thiết của bài toán: \(\frac{1}{5}\angle xOz = \frac{1}{4}\angle yOz\), tìm được \(\angle yOz\) theo \(\angle xOz\)
Vì hai góc \(xOz\) và \(yOz\) là hai góc kề nhau nên \(\angle xOy = \angle xOz + \angle yOz\)
Từ đó tính được \(\angle xOz\)
Cách giải:
Ta có: \(\frac{1}{5}\angle xOz = \frac{1}{4}\angle yOz\) suy ra \(\angle yOz = \frac{4}{5}\angle xOz\)
Vì hai góc \(xOz\) và \(yOz\) là hai góc kề nhau nên \(\angle xOy = \angle xOz + \angle yOz = {90^0}\)
\(\begin{array}{l} \Rightarrow \angle xOz + \frac{4}{5}\angle xOz = {90^0}\\ \Rightarrow \left( {1 + \frac{4}{5}} \right).\angle xOz = {90^0}\\ \Rightarrow \frac{9}{5}.\angle xOz = {90^0}\\ \Rightarrow \angle xOz = {90^0}:\frac{9}{5} = {90^0}.\frac{5}{9}\\ \Rightarrow \angle xOz = {50^0}\end{array}\)
Vậy \(\angle xOz = {50^0}\)
Chọn B.
Câu 6
Phương pháp:
Vận dụng tính chất của tam giác cân: Tam giác cân có hai góc ở đáy bằng nhau.
Áp dụng định lý tổng ba góc trong tam giác: Tổng số đo ba góc trong một tam giác bằng \({180^0}\).
Cách giải:
Tam giác \(ABC\) có: \(AB = AC\) nên \(ABC\) là tam giác cân
Suy ra \(\angle B = \angle C = {55^0}\) (tính chất của tam giác cân)
Xét tam giác \(ABC\) có: \(\angle A + \angle B + \angle C = {180^0}\) (định lý tổng ba góc trong một tam giác)
\(\begin{array}{l} \Rightarrow \angle A + {55^0} + {55^0} = {180^0}\\ \Rightarrow x + {110^0} = {180^0}\\ \Rightarrow x = {180^0} - {110^0}\\ \Rightarrow x = {70^0}\end{array}\)
Vậy \(x = {70^0}\)
Chọn D.
Câu 7
Phương pháp:
Vận dụng định lý (trường hợp bằng nhau góc – cạnh – góc (g.c.g)): Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
Cách giải:
Để \(\Delta ABC = \Delta MNP\left( {g.c.g} \right)\) thì cần thêm điều kiện \(BC = NP\).
Chọn C.
Câu 8
Phương pháp:
Vận dụng tính chất của hai đường thẳng song song: Hai đường thẳng song song thì hai góc ở vị trí so le trong bằng nhau.
Cách giải:
Ta có: \(a//b\) (giả thiết) nên \(\angle BAb = \angle ABH = {55^0}\) (hai góc so le trong)
Vậy \(\angle ABH = {55^0}\)
Chọn C.
Câu 9
Phương pháp:
Định lí là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … thì ….
Cách giải:
Định lí là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … thì ….
Chọn A.
Câu 10
Phương pháp:
Phân tích dữ liệu biểu đồ đoạn thẳng.
Cách giải:
Từ biểu đồ đoạn thẳng, ta thấy: Thời điểm nhiệt độ thấp nhất là 7 giờ; thời điểm nhiệt độ cao nhất là 13 giờ đến 16 giờ.
Chọn A.
Phần II. Tự luận:
Bài 1
Phương pháp:
a) Thực hiện phép cộng, trừ, nhân, chia với các số hữu tỉ.
b) Tính lũy thừa của một số hữu tỉ: \({\left( {\frac{a}{b}} \right)^n} = \frac{{{a^n}}}{{{b^n}}}\,\,\left( {b \ne 0;n \in \mathbb{Z}} \right)\)
Thực hiện phép cộng, trừ, nhân với các số hữu tỉ.
c) Tính căn bậc hai số học.
Thực hiện phép trừ, chia với các số hữu tỉ.
d) Tính căn bậc hai số học, tính lũy thừa của một số hữu tỉ: \({\left( {\frac{a}{b}} \right)^n} = \frac{{{a^n}}}{{{b^n}}}\,\,\left( {b \ne 0;n \in \mathbb{Z}} \right)\), tính giá trị tuyệt đối của một số.
Cách giải:
a) \(3,5.\frac{2}{{21}} - \frac{5}{9}:\frac{{25}}{3} + \frac{1}{{15}}\)
\(\begin{array}{l} = \frac{7}{2}.\frac{2}{{21}} - \frac{5}{9}.\frac{3}{{25}} + \frac{1}{{15}}\\ = \frac{1}{3} - \frac{1}{{15}} + \frac{1}{{15}}\\ = \frac{1}{3} + \left( { - \frac{1}{{15}} + \frac{1}{{15}}} \right)\\ = \frac{1}{3} + 0 = \frac{1}{3}\end{array}\)
b) \(16.{\left( {\frac{3}{{20}} - \frac{2}{5}} \right)^2} + \frac{3}{5}\)
\(\begin{array}{l} = 16.{\left( {\frac{3}{{20}} - \frac{8}{{20}}} \right)^2} + \frac{3}{5}\\ = 16.{\left( {\frac{{ - 5}}{{20}}} \right)^2} + \frac{3}{5}\\ = 16.{\left( {\frac{{ - 1}}{4}} \right)^2} + \frac{3}{5}\\ = 16.\frac{{{{\left( { - 1} \right)}^2}}}{{{4^2}}} + \frac{3}{5}\\ = 16.\frac{1}{{16}} + \frac{3}{5}\\ = 1 + \frac{3}{5} = \frac{5}{5} + \frac{3}{5}\\ = \frac{8}{5}\end{array}\)
c) \(\frac{{ - 11}}{3}:\left( {1,5.\sqrt {\frac{{16}}{9}} - \frac{{10}}{3}} \right)\)
\(\begin{array}{l} = \frac{{ - 11}}{3}:\left( {\frac{3}{2}.\frac{4}{3} - \frac{{10}}{3}} \right)\\ = \frac{{ - 11}}{3}:\left( {\frac{6}{3} - \frac{{10}}{3}} \right)\\ = \frac{{ - 11}}{3}:\frac{{ - 4}}{3}\\ = \frac{{ - 11}}{3}.\frac{3}{{ - 4}}\\ = \frac{{11}}{4}\end{array}\)
d) \(\left( {\sqrt {\frac{{81}}{{16}}} + \frac{{ - 3}}{4}} \right):{\left( { - \frac{3}{4}} \right)^2} - \left| {\frac{{ - 27}}{4}:{3^2}} \right|\)
\(\begin{array}{l} = \left( {\frac{9}{4} + \frac{{ - 3}}{4}} \right):\frac{{{{\left( { - 3} \right)}^2}}}{{{4^2}}} - \left| {\frac{{ - 27}}{4}.\frac{1}{{{3^2}}}} \right|\\ = \frac{6}{4}:\frac{9}{{16}} - \left| {\frac{{ - 27}}{4}.\frac{1}{9}} \right|\\ = \frac{6}{4}.\frac{{16}}{9} - \left| {\frac{{ - 3}}{4}} \right|\\ = \frac{8}{3} - \left[ { - \left( { - \frac{3}{4}} \right)} \right]\\ = \frac{8}{3} - \frac{3}{4} = \frac{{32}}{{12}} - \frac{9}{{12}}\\ = \frac{{23}}{{12}}\end{array}\)
Bài 2
Phương pháp:
a) Thực hiện phép nhân, chia các số hữu tỉ tìm \(x\).
b) Giải \({a^{f\left( x \right)}} = {a^{g\left( x \right)}} \Rightarrow f\left( x \right) = g\left( x \right)\)
c) Tính căn bậc hai số học, vận dụng quy tắc chuyển vế tìm \(x\).
d) Giải \(A\left( x \right).B\left( x \right) = 0\)
Trường hợp 1: Giải \(A\left( x \right) = 0\)
Trường hợp 2: Giải \(B\left( x \right) = 0\)
\(\left| {A\left( x \right)} \right| = 0\) suy ra \(A\left( x \right) = 0\)
Cách giải:
a) \(\frac{1}{3}:x = 2\frac{2}{3}:\left( { - 0,3} \right)\)
\(\begin{array}{l}\frac{1}{3}:x = \frac{8}{3}:\frac{{ - 3}}{{10}}\\\frac{1}{3}:x = \frac{8}{3}.\frac{{10}}{{ - 3}}\\\frac{1}{3}:x = \frac{{80}}{{ - 9}}\\x = \frac{1}{3}:\frac{{80}}{{ - 9}} = \frac{1}{3}.\frac{{ - 9}}{{80}}\\x = \frac{{ - 3}}{{80}}\end{array}\)
Vậy \(x = \frac{{ - 3}}{{80}}\)
b) \({3^{2x}} - {2.3^5} = {3^5}\)
\(\begin{array}{l}{3^{2x}} = {3^5} + {2.3^5}\\{3^{2x}} = \left( {1 + 2} \right){.3^5}\\{3^{2x}} = {3.3^5} = {3^1}{.3^5}\\{3^{2x}} = {3^{1 + 5}}\\{3^{2x}} = {3^6}\\ \Rightarrow 2x = 6\\\,\,\,\,\,\,\,\,\,\,x = 6:2\\\,\,\,\,\,\,\,\,\,\,x = 3\end{array}\)
Vậy \(x = 3\)
c) \(2x - \sqrt {1,69} = \sqrt {1,21} \)
\(\begin{array}{l}2x - 1,3 = 1,1\\2x = 1,1 + 1,3\\2x = 2,4\\x = 2,4:2\\x = 1,2\end{array}\)
Vậy \(x = 1,2\)
d) \(\left| {x + \frac{1}{3}} \right|.\left( {{x^2} + 1} \right) = 0\)
Trường hợp 1:
\(\begin{array}{l}\left| {x + \frac{1}{3}} \right| = 0\\x + \frac{1}{3} = 0\\x = \frac{{ - 1}}{3}\end{array}\)
Trường hợp 2: \({x^2} + 1 = 0\)
Vì \({x^2} \ge 0\) với mọi \(x\) nên \({x^2} + 1 \ge 1 > 0\) với mọi \(x\)
Do đó, không có \(x\) thỏa mãn \({x^2} + 1 = 0\)
Vậy \(x = - \frac{1}{3}\)
Bài 3
Phương pháp:
Vận dụng tính chất tia phân giác của một góc
Dấu hiệu nhận biết hai góc kề bù
Cách giải:
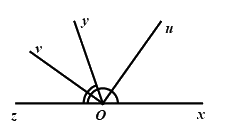
Vì \(Ou\) là tia phân giác của \(\angle xOy\) nên \(\angle xOy = 2\angle uOy\) (tính chất tia phân giác của một góc)
\(Ov\) là tia phân giác của \(\angle yOz\) nên \(\angle yOz = 2\angle yOv\) (tính chất tia phân giác của một góc)
Ta có: \(\angle xOy + \angle yOz = 2\angle uOy + 2\angle yOv\)
\(\begin{array}{l} = 2.\left( {\angle uOy + \angle yOv} \right)\\ = 2.\angle uOv\\ = {2.90^0} = {180^0}\end{array}\)
Do đó, hai góc \(xOy\) và \(yOz\) là hai góc kề bù.
Bài 4
Phương pháp:
a) Xét \(\Delta MPB\) và \(\Delta MQC\), chứng minh hai tam giác bằng nhau từ đó suy ra các cặp cạnh bằng nhau.
b) Vận dụng tính chất đường trung trực của đoạn thẳng.
Cách giải:
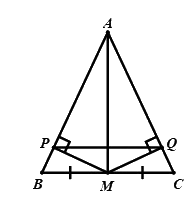
a) Vì tam giác \(ABC\) cân tại \(A\) (giả thiết) nên \(\angle ABC = \angle ACB\) (tính chất của tam giác cân) suy ra \(\angle PBM = \angle QCM\)
Vì \(M\) là trung điểm của \(BC\) nên \(BM = MC\) (tính chất trung điểm của đoạn thẳng)
Vì \(MP,MQ\) lần lượt vuông góc với \(AB,AC\) nên ta có: \(\angle BPM = \angle APM = {90^0}\,;\,\angle CQM = \angle AQM = {90^0}\)
*Xét \(\Delta MPB\) và \(\Delta MQC\) có:
\(\angle BPM = \angle CQM = {90^0}\) (chứng minh trên)
\(BM = MC\) (chứng minh trên)
\(\angle PBM = \angle QCM\) (chứng minh trên)
Suy ra \(\Delta MPB = \Delta MQC\) (cạnh huyền – góc nhọn)
\( \Rightarrow MP = MQ\) (hai cạnh tương ứng)
và \(BP = QC\) (hai cạnh tương ứng)
Ta có:
\(P\) nằm giữa \(A\) và \(B\) nên \(AB = AP + BP \Rightarrow AP = AB - BP\)
\(Q\) nằm giữa \(A\) và \(C\) nên \(AC = AQ + QC \Rightarrow AQ = AC - QC\)
Mà \(AB = AC\) (do tam giác \(ABC\) cân tại \(A\)); \(BP = QC\) (chứng minh trên)
Do đó, \(AP = AQ\) (điều phải chứng minh)
b) Ta có: \(AP = AQ;MP = MQ\) nên \(A,M\)cùng cách đều hai điểm \(P,Q\) nên \(AM\) là đường trung trực của đoạn thẳng \(PQ\).
Do đó, \(AM\) vuông góc với \(PQ\).
Bài 5
Phương pháp:
Vận dụng kiến thức lũy thừa của một số và căn bậc hai số học của một số.
Cách giải:
Ta có: \({x^2} \ge 0\) với mọi số thực \(x\) nên \({x^2} + 81 \ge 81\) với mọi số thực \(x\).
Suy ra \(\sqrt {{x^2} + 81} \ge \sqrt {81} = 9\) với mọi số thực \(x\).
Do đó, \( - \sqrt {{x^2} + 81} \le - 9\) với mọi số thực \(x\).
Suy ra \(A = - \sqrt {{x^2} + 81} + 2030 \le - 9 + 2030\) hay \(A \le 2021\) với mọi số thực \(x\).
Vậy giá trị lớn nhất của \(A\) là \(2021\).
Dấu “=” xảy ra khi và chỉ khi \( \Leftrightarrow {x^2} = 0 \Leftrightarrow x = 0\).
I. TRẮC NGHIỆM ( 3 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Các số hữu tỉ \(\frac{{ - 5}}{{11}}\,\,;\,\,\frac{{ - 5}}{9}\,\,;\,\,\frac{7}{5}\,\,;\,\,\frac{3}{5}\,\,;\,\,\frac{{18}}{{13}}\) được sắp xếp theo thứ tự tăng dần là:
A. \(\frac{{ - 5}}{{11}}\,\,;\,\,\frac{{ - 5}}{9}\,\,;\,\,\frac{{18}}{{13}}\,\,;\,\,\frac{7}{5}\,\,;\,\,\frac{3}{5}.\)
B. \(\frac{{ - 5}}{9}\,\,;\,\,\frac{{ - 5}}{{11}}\,\,;\,\,\frac{3}{5}\,\,;\,\,\frac{{18}}{{13}}\,\,;\frac{7}{5}.\)
C. \(\frac{{ - 5}}{{11}}\,\,;\,\,\frac{{ - 5}}{9}\,\,;\,\,\frac{3}{5}\,\,;\,\,\frac{{18}}{{13}}\,\,;\,\,\frac{7}{5}.\)
D. \(\frac{{ - 5}}{9}\,\,;\,\,\frac{{ - 5}}{{11}}\,\,;\,\,\frac{3}{5}\,\,;\,\,\frac{7}{5}\,\,;\,\,\frac{{18}}{{13}}.\)
Câu 2: Kết quả của phép tính: \(\frac{{{3^{10}}}}{{{5^{10}}}}{.5^{10}}\) là:
A. \({3^5}\)
B. \({3^{20}}\)
C. \({3^{10}}\)
D. \({5.3^{10}}\)
Câu 3: Kết quả của phép tính: \(\sqrt {0,04} + \sqrt {0,25} + 2,31\) là:
A. \(2,53\)
B. \(2,96\)
C. \(2,6\)
D. \(3,01\)
Câu 4: Cho \(x,y\) là hai số thực tùy ý. Khẳng định nào sau đây đúng?
A. \(\left| {x - y} \right| = x - y\)
B. \(\left| {x - y} \right| = \left| x \right| - \left| y \right|\)
C. \(\left| {x + y} \right| = \left| x \right| + \left| y \right|\)
D. \(\left| {x + y} \right| = \left| x \right| - \left| y \right|\)nếu \(x > 0 > y\) và \(\left| x \right| \ge \left| y \right|\)
Câu 5: Quan sát hình vẽ bên dưới:
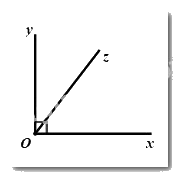
Tính số đo góc \(xOz\), biết \(\frac{1}{5}\angle xOz = \frac{1}{4}\angle yOz\).
A. \(\angle xOz = {40^0}\)
B. \(\angle xOz = {50^0}\)
C. \(\angle xOz = {30^0}\)
D. \(\angle xOz = {60^0}\)
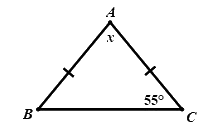
Câu 6: Tìm số đo của \(x\) trong hình vẽ dưới đây?
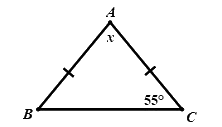
A. \(x = {55^0}\)
B. \(x = {75^0}\)
C. \(x = {60^0}\)
D. \(x = {70^0}\)
Câu 7: Cho hai tam giác \(ABC\) và \(MNP\) có \(\angle ABC = \angle MNP,\angle ACB = \angle MPN\). Cần thêm một điều kiện để tam giác \(ABC\) và tam giác \(MNP\) bằng nhau theo trường hợp góc – cạnh – góc là:
A. \(AC = MP\)
B. \(AB = MN\)
C. \(BC = NP\)
D. \(AC = MN\)
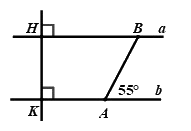
Câu 8: Quan sát hình vẽ bên dưới, tính số đo góc \(\angle ABH\) biết \(a//b\).
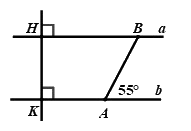
A. \(\angle ABH = {125^0}\)
B. \(\angle ABH = {65^0}\)
C. \(\angle ABH = {55^0}\)
D. \(\angle ABH = {95^0}\)
Câu 9: Điền cụm từ còn thiếu vào …: “Định lí …”
A. là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … thì ….
B. là một câu nói được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … thì ….
C. là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … vậy….
D. là một câu nói được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … vậy ….
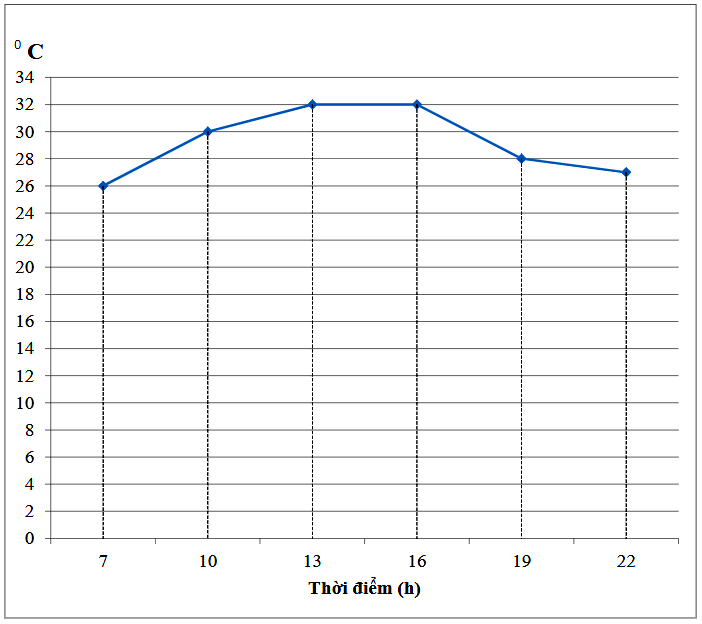
Câu 10: Biểu đồ đoạn thẳng trên cho biết nhiệt độ ở Hà Nội trong ngày 07/05/2021 tại một số thời điểm. Hãy cho biết thời điểm nào nhiệt độ thấp nhất, cao nhất?
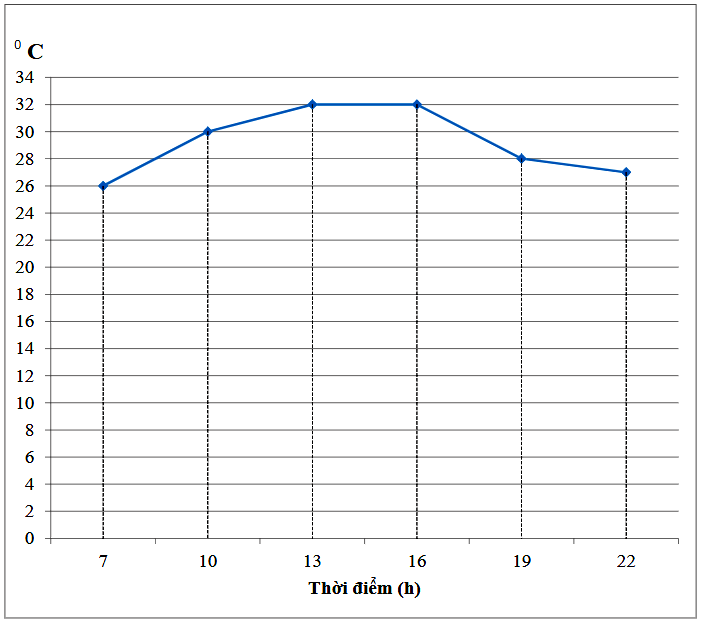
A. Thời điểm nhiệt độ thấp nhất là 26 độ C; thời điểm nhiệt độ cao nhất là 32 độ C.
B. Thời điểm nhiệt độ thấp nhất là 22 độ C; thời điểm nhiệt độ cao nhất là 32 độ C
C. Thời điểm nhiệt độ thấp nhất là 22 giờ; thời điểm nhiệt độ cao nhất là 13 giờ đến 16 giờ.
D. Thời điểm nhiệt độ thấp nhất là 7 giờ; thời điểm nhiệt độ cao nhất là 13 giờ đến 16 giờ.
Phần II. Tự luận (7 điểm):
Bài 1: (2,0 điểm)
Thực hiện phép tính:
a) \(3,5.\frac{2}{{21}} - \frac{5}{9}:\frac{{25}}{3} + \frac{1}{{15}}\)
b) \(16.{\left( {\frac{3}{{20}} - \frac{2}{5}} \right)^2} + \frac{3}{5}\)
c) \(\frac{{ - 11}}{3}:\left( {1,5.\sqrt {\frac{{16}}{9}} - \frac{{10}}{3}} \right)\)
d) \(\left( {\sqrt {\frac{{81}}{{16}}} + \frac{{ - 3}}{4}} \right):{\left( { - \frac{3}{4}} \right)^2} - \left| {\frac{{ - 27}}{4}:{3^2}} \right|\)
Bài 2: ( 2 điểm) Tìm \(x\), biết:
a) \(\frac{1}{3}:x = 2\frac{2}{3}:\left( { - 0,3} \right)\)
b) \({3^{2x}} - {2.3^5} = {3^5}\)
c) \(2x - \sqrt {1,69} = \sqrt {1,21} \)
d) \(\left| {x + \frac{1}{3}} \right|.\left( {{x^2} + 1} \right) = 0\)
Bài 3: (1 điểm) Cho góc vuông \(uOv\) và tia \(Oy\) đi qua một điểm trong của góc đó. Vẽ tia \(Ox\) sao cho \(Ou\) là tia phân giác của góc \(xOy\). Vẽ tia \(Oz\) sao cho \(Ov\) là tia phân giác của góc \(yOz\). Chứng minh rằng hai góc \(xOy\) và \(yOz\) là hai góc kề bù.
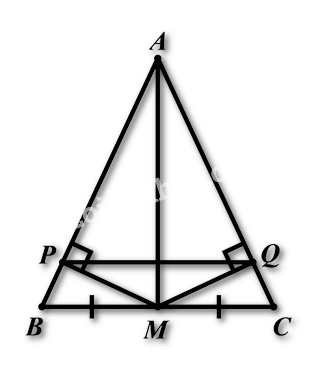
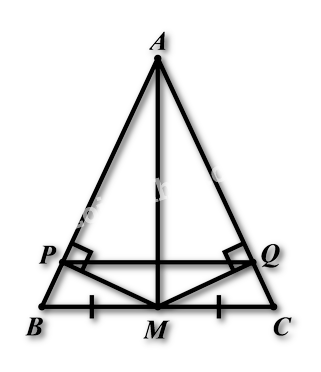
Bài 4: (1,5 điểm) Cho tam giác \(ABC\) cân tại đỉnh \(A\). Gọi \(M\) là trung điểm của \(BC\). Trên cạnh \(AB\) và \(AC\) lấy các điểm \(P,Q\) sao cho \(MP,MQ\) lần lượt vuông góc với \(AB,AC\).
a) Chứng minh rằng: \(MP = MQ\) và \(AP = AQ\).
b) Đường thẳng \(PQ\) có vuông góc với \(AM\) không? Vì sao?
Bài 5 (0,5 điểm): Tìm giá trị lớn nhất của biểu thức: \(A = - \sqrt {{x^2} + 81} + 2030.\)
I. TRẮC NGHIỆM ( 3 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Các số hữu tỉ \(\frac{{ - 5}}{{11}}\,\,;\,\,\frac{{ - 5}}{9}\,\,;\,\,\frac{7}{5}\,\,;\,\,\frac{3}{5}\,\,;\,\,\frac{{18}}{{13}}\) được sắp xếp theo thứ tự tăng dần là:
A. \(\frac{{ - 5}}{{11}}\,\,;\,\,\frac{{ - 5}}{9}\,\,;\,\,\frac{{18}}{{13}}\,\,;\,\,\frac{7}{5}\,\,;\,\,\frac{3}{5}.\)
B. \(\frac{{ - 5}}{9}\,\,;\,\,\frac{{ - 5}}{{11}}\,\,;\,\,\frac{3}{5}\,\,;\,\,\frac{{18}}{{13}}\,\,;\frac{7}{5}.\)
C. \(\frac{{ - 5}}{{11}}\,\,;\,\,\frac{{ - 5}}{9}\,\,;\,\,\frac{3}{5}\,\,;\,\,\frac{{18}}{{13}}\,\,;\,\,\frac{7}{5}.\)
D. \(\frac{{ - 5}}{9}\,\,;\,\,\frac{{ - 5}}{{11}}\,\,;\,\,\frac{3}{5}\,\,;\,\,\frac{7}{5}\,\,;\,\,\frac{{18}}{{13}}.\)
Câu 2: Kết quả của phép tính: \(\frac{{{3^{10}}}}{{{5^{10}}}}{.5^{10}}\) là:
A. \({3^5}\)
B. \({3^{20}}\)
C. \({3^{10}}\)
D. \({5.3^{10}}\)
Câu 3: Kết quả của phép tính: \(\sqrt {0,04} + \sqrt {0,25} + 2,31\) là:
A. \(2,53\)
B. \(2,96\)
C. \(2,6\)
D. \(3,01\)
Câu 4: Cho \(x,y\) là hai số thực tùy ý. Khẳng định nào sau đây đúng?
A. \(\left| {x - y} \right| = x - y\)
B. \(\left| {x - y} \right| = \left| x \right| - \left| y \right|\)
C. \(\left| {x + y} \right| = \left| x \right| + \left| y \right|\)
D. \(\left| {x + y} \right| = \left| x \right| - \left| y \right|\)nếu \(x > 0 > y\) và \(\left| x \right| \ge \left| y \right|\)
Câu 5: Quan sát hình vẽ bên dưới:
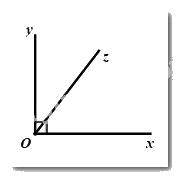
Tính số đo góc \(xOz\), biết \(\frac{1}{5}\angle xOz = \frac{1}{4}\angle yOz\).
A. \(\angle xOz = {40^0}\)
B. \(\angle xOz = {50^0}\)
C. \(\angle xOz = {30^0}\)
D. \(\angle xOz = {60^0}\)
Câu 6: Tìm số đo của \(x\) trong hình vẽ dưới đây?
A. \(x = {55^0}\)
B. \(x = {75^0}\)
C. \(x = {60^0}\)
D. \(x = {70^0}\)
Câu 7: Cho hai tam giác \(ABC\) và \(MNP\) có \(\angle ABC = \angle MNP,\angle ACB = \angle MPN\). Cần thêm một điều kiện để tam giác \(ABC\) và tam giác \(MNP\) bằng nhau theo trường hợp góc – cạnh – góc là:
A. \(AC = MP\)
B. \(AB = MN\)
C. \(BC = NP\)
D. \(AC = MN\)
Câu 8: Quan sát hình vẽ bên dưới, tính số đo góc \(\angle ABH\) biết \(a//b\).
A. \(\angle ABH = {125^0}\)
B. \(\angle ABH = {65^0}\)
C. \(\angle ABH = {55^0}\)
D. \(\angle ABH = {95^0}\)
Câu 9: Điền cụm từ còn thiếu vào …: “Định lí …”
A. là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … thì ….
B. là một câu nói được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … thì ….
C. là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … vậy….
D. là một câu nói được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … vậy ….
Câu 10: Biểu đồ đoạn thẳng trên cho biết nhiệt độ ở Hà Nội trong ngày 07/05/2021 tại một số thời điểm. Hãy cho biết thời điểm nào nhiệt độ thấp nhất, cao nhất?
A. Thời điểm nhiệt độ thấp nhất là 26 độ C; thời điểm nhiệt độ cao nhất là 32 độ C.
B. Thời điểm nhiệt độ thấp nhất là 22 độ C; thời điểm nhiệt độ cao nhất là 32 độ C
C. Thời điểm nhiệt độ thấp nhất là 22 giờ; thời điểm nhiệt độ cao nhất là 13 giờ đến 16 giờ.
D. Thời điểm nhiệt độ thấp nhất là 7 giờ; thời điểm nhiệt độ cao nhất là 13 giờ đến 16 giờ.
Phần II. Tự luận (7 điểm):
Bài 1: (2,0 điểm)
Thực hiện phép tính:
a) \(3,5.\frac{2}{{21}} - \frac{5}{9}:\frac{{25}}{3} + \frac{1}{{15}}\)
b) \(16.{\left( {\frac{3}{{20}} - \frac{2}{5}} \right)^2} + \frac{3}{5}\)
c) \(\frac{{ - 11}}{3}:\left( {1,5.\sqrt {\frac{{16}}{9}} - \frac{{10}}{3}} \right)\)
d) \(\left( {\sqrt {\frac{{81}}{{16}}} + \frac{{ - 3}}{4}} \right):{\left( { - \frac{3}{4}} \right)^2} - \left| {\frac{{ - 27}}{4}:{3^2}} \right|\)
Bài 2: ( 2 điểm) Tìm \(x\), biết:
a) \(\frac{1}{3}:x = 2\frac{2}{3}:\left( { - 0,3} \right)\)
b) \({3^{2x}} - {2.3^5} = {3^5}\)
c) \(2x - \sqrt {1,69} = \sqrt {1,21} \)
d) \(\left| {x + \frac{1}{3}} \right|.\left( {{x^2} + 1} \right) = 0\)
Bài 3: (1 điểm) Cho góc vuông \(uOv\) và tia \(Oy\) đi qua một điểm trong của góc đó. Vẽ tia \(Ox\) sao cho \(Ou\) là tia phân giác của góc \(xOy\). Vẽ tia \(Oz\) sao cho \(Ov\) là tia phân giác của góc \(yOz\). Chứng minh rằng hai góc \(xOy\) và \(yOz\) là hai góc kề bù.
Bài 4: (1,5 điểm) Cho tam giác \(ABC\) cân tại đỉnh \(A\). Gọi \(M\) là trung điểm của \(BC\). Trên cạnh \(AB\) và \(AC\) lấy các điểm \(P,Q\) sao cho \(MP,MQ\) lần lượt vuông góc với \(AB,AC\).
a) Chứng minh rằng: \(MP = MQ\) và \(AP = AQ\).
b) Đường thẳng \(PQ\) có vuông góc với \(AM\) không? Vì sao?
Bài 5 (0,5 điểm): Tìm giá trị lớn nhất của biểu thức: \(A = - \sqrt {{x^2} + 81} + 2030.\)
Phần I: Trắc nghiệm
1.B | 2.C | 3.D | 4.D | 5.B | 6.D | 7.C | 8.C | 9.A | 10.A |
Câu 1
Phương pháp:
Quy đồng các phân số cùng mẫu dương để so sánh.
Cách giải:
*Ta có: \(11 < 9\), do đó, \(\frac{5}{{11}} < \frac{5}{9}\) suy ra \(\frac{{ - 5}}{{11}} > \frac{{ - 5}}{9}\)
*Ta có: \(\frac{7}{5} = \frac{{91}}{{65}}\,\,;\,\,\frac{3}{5} = \frac{{39}}{{65}}\,\,;\,\,\frac{{18}}{{13}} = \frac{{90}}{{65}}\)
Vì \(39 < 90 < 91\) nên \(\frac{{39}}{{65}} < \frac{{90}}{{65}} < \frac{{91}}{{65}}\) hay \(\frac{3}{5} < \frac{{18}}{{13}} < \frac{7}{5}\)
Thứ tự tăng dần của các số hữu tỉ là: \(\frac{{ - 5}}{{9}}\,\,;\,\,\frac{{ - 5}}{11}\,\,;\,\,\frac{3}{5}\,\,;\,\,\frac{{18}}{{13}}\,\,;\,\,\frac{7}{5}.\)
Chọn B.
Câu 2
Phương pháp:
Vận dụng công thức tính lũy thừa của một thường bằng thương các lũy thừa: \({\left( {\frac{x}{y}} \right)^n} = \frac{{{x^n}}}{{{y^n}}}\,\left( {y \ne 0} \right)\)
Cách giải:
\({\left( {\frac{3}{5}} \right)^{10}}:{5^{10}}\)\( = \frac{{{3^{10}}}}{{{5^{10}}}}{.5^{10}} = {3^{10}}\)
Chọn C.
Câu 3
Phương pháp:
Thực hiện tính căn bậc hai.
Cách giải:
\(\begin{array}{l}\,\,\,\,\sqrt {0,04} + \sqrt {0,25} + 2,31\\ = 0,2 + 0,5 + 2,31\\ = 0,7 + 2,31\\ = 3,01\end{array}\)
Chọn D.
Câu 4
Phương pháp:
Vận dụng kiến thức về dấu giá trị tuyệt đối của một số.
Cách giải:
+ Đáp án A sai, khi \(x < y\)
+ Đáp án B sai, lấy ví dụ khi \(x = 0;y \ne 0\)
+ Đáp án C sai, lấy ví dụ khi \(x = - y \ne 0\)
+ Đáp án D đúng, theo quy tắc cộng hai số trái dấu.
Chọn D.
Câu 5
Phương pháp:
Từ giả thiết của bài toán: \(\frac{1}{5}\angle xOz = \frac{1}{4}\angle yOz\), tìm được \(\angle yOz\) theo \(\angle xOz\)
Vì hai góc \(xOz\) và \(yOz\) là hai góc kề nhau nên \(\angle xOy = \angle xOz + \angle yOz\)
Từ đó tính được \(\angle xOz\)
Cách giải:
Ta có: \(\frac{1}{5}\angle xOz = \frac{1}{4}\angle yOz\) suy ra \(\angle yOz = \frac{4}{5}\angle xOz\)
Vì hai góc \(xOz\) và \(yOz\) là hai góc kề nhau nên \(\angle xOy = \angle xOz + \angle yOz = {90^0}\)
\(\begin{array}{l} \Rightarrow \angle xOz + \frac{4}{5}\angle xOz = {90^0}\\ \Rightarrow \left( {1 + \frac{4}{5}} \right).\angle xOz = {90^0}\\ \Rightarrow \frac{9}{5}.\angle xOz = {90^0}\\ \Rightarrow \angle xOz = {90^0}:\frac{9}{5} = {90^0}.\frac{5}{9}\\ \Rightarrow \angle xOz = {50^0}\end{array}\)
Vậy \(\angle xOz = {50^0}\)
Chọn B.
Câu 6
Phương pháp:
Vận dụng tính chất của tam giác cân: Tam giác cân có hai góc ở đáy bằng nhau.
Áp dụng định lý tổng ba góc trong tam giác: Tổng số đo ba góc trong một tam giác bằng \({180^0}\).
Cách giải:
Tam giác \(ABC\) có: \(AB = AC\) nên \(ABC\) là tam giác cân
Suy ra \(\angle B = \angle C = {55^0}\) (tính chất của tam giác cân)
Xét tam giác \(ABC\) có: \(\angle A + \angle B + \angle C = {180^0}\) (định lý tổng ba góc trong một tam giác)
\(\begin{array}{l} \Rightarrow \angle A + {55^0} + {55^0} = {180^0}\\ \Rightarrow x + {110^0} = {180^0}\\ \Rightarrow x = {180^0} - {110^0}\\ \Rightarrow x = {70^0}\end{array}\)
Vậy \(x = {70^0}\)
Chọn D.
Câu 7
Phương pháp:
Vận dụng định lý (trường hợp bằng nhau góc – cạnh – góc (g.c.g)): Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
Cách giải:
Để \(\Delta ABC = \Delta MNP\left( {g.c.g} \right)\) thì cần thêm điều kiện \(BC = NP\).
Chọn C.
Câu 8
Phương pháp:
Vận dụng tính chất của hai đường thẳng song song: Hai đường thẳng song song thì hai góc ở vị trí so le trong bằng nhau.
Cách giải:
Ta có: \(a//b\) (giả thiết) nên \(\angle BAb = \angle ABH = {55^0}\) (hai góc so le trong)
Vậy \(\angle ABH = {55^0}\)
Chọn C.
Câu 9
Phương pháp:
Định lí là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … thì ….
Cách giải:
Định lí là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … thì ….
Chọn A.
Câu 10
Phương pháp:
Phân tích dữ liệu biểu đồ đoạn thẳng.
Cách giải:
Từ biểu đồ đoạn thẳng, ta thấy: Thời điểm nhiệt độ thấp nhất là 7 giờ; thời điểm nhiệt độ cao nhất là 13 giờ đến 16 giờ.
Chọn A.
Phần II. Tự luận:
Bài 1
Phương pháp:
a) Thực hiện phép cộng, trừ, nhân, chia với các số hữu tỉ.
b) Tính lũy thừa của một số hữu tỉ: \({\left( {\frac{a}{b}} \right)^n} = \frac{{{a^n}}}{{{b^n}}}\,\,\left( {b \ne 0;n \in \mathbb{Z}} \right)\)
Thực hiện phép cộng, trừ, nhân với các số hữu tỉ.
c) Tính căn bậc hai số học.
Thực hiện phép trừ, chia với các số hữu tỉ.
d) Tính căn bậc hai số học, tính lũy thừa của một số hữu tỉ: \({\left( {\frac{a}{b}} \right)^n} = \frac{{{a^n}}}{{{b^n}}}\,\,\left( {b \ne 0;n \in \mathbb{Z}} \right)\), tính giá trị tuyệt đối của một số.
Cách giải:
a) \(3,5.\frac{2}{{21}} - \frac{5}{9}:\frac{{25}}{3} + \frac{1}{{15}}\)
\(\begin{array}{l} = \frac{7}{2}.\frac{2}{{21}} - \frac{5}{9}.\frac{3}{{25}} + \frac{1}{{15}}\\ = \frac{1}{3} - \frac{1}{{15}} + \frac{1}{{15}}\\ = \frac{1}{3} + \left( { - \frac{1}{{15}} + \frac{1}{{15}}} \right)\\ = \frac{1}{3} + 0 = \frac{1}{3}\end{array}\)
b) \(16.{\left( {\frac{3}{{20}} - \frac{2}{5}} \right)^2} + \frac{3}{5}\)
\(\begin{array}{l} = 16.{\left( {\frac{3}{{20}} - \frac{8}{{20}}} \right)^2} + \frac{3}{5}\\ = 16.{\left( {\frac{{ - 5}}{{20}}} \right)^2} + \frac{3}{5}\\ = 16.{\left( {\frac{{ - 1}}{4}} \right)^2} + \frac{3}{5}\\ = 16.\frac{{{{\left( { - 1} \right)}^2}}}{{{4^2}}} + \frac{3}{5}\\ = 16.\frac{1}{{16}} + \frac{3}{5}\\ = 1 + \frac{3}{5} = \frac{5}{5} + \frac{3}{5}\\ = \frac{8}{5}\end{array}\)
c) \(\frac{{ - 11}}{3}:\left( {1,5.\sqrt {\frac{{16}}{9}} - \frac{{10}}{3}} \right)\)
\(\begin{array}{l} = \frac{{ - 11}}{3}:\left( {\frac{3}{2}.\frac{4}{3} - \frac{{10}}{3}} \right)\\ = \frac{{ - 11}}{3}:\left( {\frac{6}{3} - \frac{{10}}{3}} \right)\\ = \frac{{ - 11}}{3}:\frac{{ - 4}}{3}\\ = \frac{{ - 11}}{3}.\frac{3}{{ - 4}}\\ = \frac{{11}}{4}\end{array}\)
d) \(\left( {\sqrt {\frac{{81}}{{16}}} + \frac{{ - 3}}{4}} \right):{\left( { - \frac{3}{4}} \right)^2} - \left| {\frac{{ - 27}}{4}:{3^2}} \right|\)
\(\begin{array}{l} = \left( {\frac{9}{4} + \frac{{ - 3}}{4}} \right):\frac{{{{\left( { - 3} \right)}^2}}}{{{4^2}}} - \left| {\frac{{ - 27}}{4}.\frac{1}{{{3^2}}}} \right|\\ = \frac{6}{4}:\frac{9}{{16}} - \left| {\frac{{ - 27}}{4}.\frac{1}{9}} \right|\\ = \frac{6}{4}.\frac{{16}}{9} - \left| {\frac{{ - 3}}{4}} \right|\\ = \frac{8}{3} - \left[ { - \left( { - \frac{3}{4}} \right)} \right]\\ = \frac{8}{3} - \frac{3}{4} = \frac{{32}}{{12}} - \frac{9}{{12}}\\ = \frac{{23}}{{12}}\end{array}\)
Bài 2
Phương pháp:
a) Thực hiện phép nhân, chia các số hữu tỉ tìm \(x\).
b) Giải \({a^{f\left( x \right)}} = {a^{g\left( x \right)}} \Rightarrow f\left( x \right) = g\left( x \right)\)
c) Tính căn bậc hai số học, vận dụng quy tắc chuyển vế tìm \(x\).
d) Giải \(A\left( x \right).B\left( x \right) = 0\)
Trường hợp 1: Giải \(A\left( x \right) = 0\)
Trường hợp 2: Giải \(B\left( x \right) = 0\)
\(\left| {A\left( x \right)} \right| = 0\) suy ra \(A\left( x \right) = 0\)
Cách giải:
a) \(\frac{1}{3}:x = 2\frac{2}{3}:\left( { - 0,3} \right)\)
\(\begin{array}{l}\frac{1}{3}:x = \frac{8}{3}:\frac{{ - 3}}{{10}}\\\frac{1}{3}:x = \frac{8}{3}.\frac{{10}}{{ - 3}}\\\frac{1}{3}:x = \frac{{80}}{{ - 9}}\\x = \frac{1}{3}:\frac{{80}}{{ - 9}} = \frac{1}{3}.\frac{{ - 9}}{{80}}\\x = \frac{{ - 3}}{{80}}\end{array}\)
Vậy \(x = \frac{{ - 3}}{{80}}\)
b) \({3^{2x}} - {2.3^5} = {3^5}\)
\(\begin{array}{l}{3^{2x}} = {3^5} + {2.3^5}\\{3^{2x}} = \left( {1 + 2} \right){.3^5}\\{3^{2x}} = {3.3^5} = {3^1}{.3^5}\\{3^{2x}} = {3^{1 + 5}}\\{3^{2x}} = {3^6}\\ \Rightarrow 2x = 6\\\,\,\,\,\,\,\,\,\,\,x = 6:2\\\,\,\,\,\,\,\,\,\,\,x = 3\end{array}\)
Vậy \(x = 3\)
c) \(2x - \sqrt {1,69} = \sqrt {1,21} \)
\(\begin{array}{l}2x - 1,3 = 1,1\\2x = 1,1 + 1,3\\2x = 2,4\\x = 2,4:2\\x = 1,2\end{array}\)
Vậy \(x = 1,2\)
d) \(\left| {x + \frac{1}{3}} \right|.\left( {{x^2} + 1} \right) = 0\)
Trường hợp 1:
\(\begin{array}{l}\left| {x + \frac{1}{3}} \right| = 0\\x + \frac{1}{3} = 0\\x = \frac{{ - 1}}{3}\end{array}\)
Trường hợp 2: \({x^2} + 1 = 0\)
Vì \({x^2} \ge 0\) với mọi \(x\) nên \({x^2} + 1 \ge 1 > 0\) với mọi \(x\)
Do đó, không có \(x\) thỏa mãn \({x^2} + 1 = 0\)
Vậy \(x = - \frac{1}{3}\)
Bài 3
Phương pháp:
Vận dụng tính chất tia phân giác của một góc
Dấu hiệu nhận biết hai góc kề bù
Cách giải:
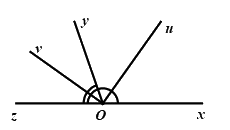
Vì \(Ou\) là tia phân giác của \(\angle xOy\) nên \(\angle xOy = 2\angle uOy\) (tính chất tia phân giác của một góc)
\(Ov\) là tia phân giác của \(\angle yOz\) nên \(\angle yOz = 2\angle yOv\) (tính chất tia phân giác của một góc)
Ta có: \(\angle xOy + \angle yOz = 2\angle uOy + 2\angle yOv\)
\(\begin{array}{l} = 2.\left( {\angle uOy + \angle yOv} \right)\\ = 2.\angle uOv\\ = {2.90^0} = {180^0}\end{array}\)
Do đó, hai góc \(xOy\) và \(yOz\) là hai góc kề bù.
Bài 4
Phương pháp:
a) Xét \(\Delta MPB\) và \(\Delta MQC\), chứng minh hai tam giác bằng nhau từ đó suy ra các cặp cạnh bằng nhau.
b) Vận dụng tính chất đường trung trực của đoạn thẳng.
Cách giải:
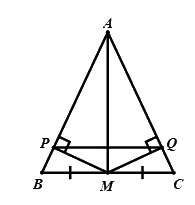
a) Vì tam giác \(ABC\) cân tại \(A\) (giả thiết) nên \(\angle ABC = \angle ACB\) (tính chất của tam giác cân) suy ra \(\angle PBM = \angle QCM\)
Vì \(M\) là trung điểm của \(BC\) nên \(BM = MC\) (tính chất trung điểm của đoạn thẳng)
Vì \(MP,MQ\) lần lượt vuông góc với \(AB,AC\) nên ta có: \(\angle BPM = \angle APM = {90^0}\,;\,\angle CQM = \angle AQM = {90^0}\)
*Xét \(\Delta MPB\) và \(\Delta MQC\) có:
\(\angle BPM = \angle CQM = {90^0}\) (chứng minh trên)
\(BM = MC\) (chứng minh trên)
\(\angle PBM = \angle QCM\) (chứng minh trên)
Suy ra \(\Delta MPB = \Delta MQC\) (cạnh huyền – góc nhọn)
\( \Rightarrow MP = MQ\) (hai cạnh tương ứng)
và \(BP = QC\) (hai cạnh tương ứng)
Ta có:
\(P\) nằm giữa \(A\) và \(B\) nên \(AB = AP + BP \Rightarrow AP = AB - BP\)
\(Q\) nằm giữa \(A\) và \(C\) nên \(AC = AQ + QC \Rightarrow AQ = AC - QC\)
Mà \(AB = AC\) (do tam giác \(ABC\) cân tại \(A\)); \(BP = QC\) (chứng minh trên)
Do đó, \(AP = AQ\) (điều phải chứng minh)
b) Ta có: \(AP = AQ;MP = MQ\) nên \(A,M\)cùng cách đều hai điểm \(P,Q\) nên \(AM\) là đường trung trực của đoạn thẳng \(PQ\).
Do đó, \(AM\) vuông góc với \(PQ\).
Bài 5
Phương pháp:
Vận dụng kiến thức lũy thừa của một số và căn bậc hai số học của một số.
Cách giải:
Ta có: \({x^2} \ge 0\) với mọi số thực \(x\) nên \({x^2} + 81 \ge 81\) với mọi số thực \(x\).
Suy ra \(\sqrt {{x^2} + 81} \ge \sqrt {81} = 9\) với mọi số thực \(x\).
Do đó, \( - \sqrt {{x^2} + 81} \le - 9\) với mọi số thực \(x\).
Suy ra \(A = - \sqrt {{x^2} + 81} + 2030 \le - 9 + 2030\) hay \(A \le 2021\) với mọi số thực \(x\).
Vậy giá trị lớn nhất của \(A\) là \(2021\).
Dấu “=” xảy ra khi và chỉ khi \( \Leftrightarrow {x^2} = 0 \Leftrightarrow x = 0\).
Đề thi học kì 1 Toán 7 - Đề số 2 chương trình Kết nối tri thức là một bài kiểm tra quan trọng đánh giá mức độ nắm vững kiến thức của học sinh sau một học kì học tập. Đề thi bao gồm các dạng bài tập khác nhau, từ trắc nghiệm đến tự luận, tập trung vào các chủ đề chính đã được học trong chương trình.
Đề thi thường bao gồm các nội dung sau:
Đề thi thường được chia thành hai phần chính:
Để đạt kết quả tốt nhất trong kỳ thi học kì 1 Toán 7, các em học sinh cần:
Việc luyện tập với đề thi học kì 1 Toán 7 - Đề số 2 - Kết nối tri thức mang lại nhiều lợi ích cho học sinh:
Giaitoan.edu.vn là một website cung cấp các tài liệu học tập trực tuyến uy tín, chất lượng dành cho học sinh các cấp. Tại đây, các em có thể tìm thấy:
Đề thi học kì 1 Toán 7 - Đề số 2 - Kết nối tri thức là một cơ hội tốt để các em học sinh ôn luyện và đánh giá kiến thức của mình. Hãy tận dụng tối đa nguồn tài liệu học tập trên Giaitoan.edu.vn để đạt kết quả tốt nhất trong kỳ thi sắp tới.