Chào mừng các em học sinh đến với lời giải chi tiết bài 55 Vở bài tập Toán 5 Cánh Diều. Bài học này tập trung vào việc ôn luyện và thực hành kiến thức về chu vi hình tròn, một khái niệm quan trọng trong chương trình Toán học lớp 5.
Giaitoan.edu.vn cung cấp lời giải dễ hiểu, kèm theo các ví dụ minh họa giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Tính chu vi của mỗi hình tròn sau: Hoàn thành bảng sau: a) Đường kính của một bánh xe ô tô là 0,6 m. Tính chu vi bánh xe đó.
Trả lời Bài 4 Trang 20 VBT Toán 5 Cánh Diều
Hai con kiến bò một vòng xung quanh một hình vuông và một hình tròn như hình vẽ dưới đây. Theo em, con kiến nào đã bò được quãng đường dài hơn? Tại sao?
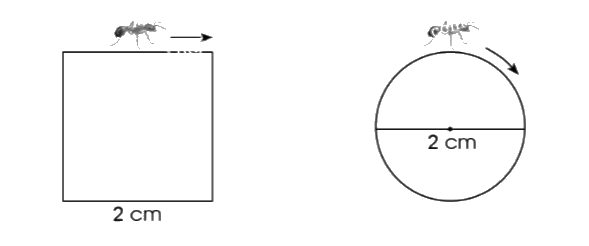
Trả lời: ...................................................................................................
Phương pháp giải:
Quãng đường 2 con kiến bò đường bằng chu vi hình vuông và chu vi hình tròn.
Lời giải chi tiết:
Quãng đường con kiến bò một vòng xung quanh một hình vuông là:
2 x 4 = 8 (cm)
Quãng đường con kiến bò một vòng xung quanh một hình tròn là:
2 x 3,14 = 6,28 (cm)
Vì 8 > 6,28 nên con kiến bò một vòng xung quanh một hình vuông đã bò được quãng đường dài hơn.
Trả lời Bài 3 Trang 19 VBT Toán 5 Cánh Diều
a) Đường kính của một bánh xe ô tô là 0,6 m. Tính chu vi bánh xe đó.
b) Bán kính của một vòng đu quay là 10 m. Nếu ngồi trên đu quay đó và quay đúng 1 vòng thì bạn đã di chuyển được bao nhiêu mét?

Phương pháp giải:
a) Muốn tính chu vi của hình tròn, ta lấy đường kính nhân với số 3,14.
b) Nếu ngồi trên đu quay đó và quay đúng 1 vòng thì quãng đường đi được chính là chu vi hình tròn.
Lời giải chi tiết:
a) Chu vi bánh xe đó là:
0,6 x 3,14 = 1,884 (m)
b) Chu vi của một vòng đu quay là:
10 x 2 x 3,14 = 62,8 (m)
Nếu ngồi trên đu quay đó và quay đúng 1 vòng thì quãng đường đi được chính là chu vi hình tròn.
Vậy bạn đã di chuyển được 62,8 m.
Trả lời Bài 2 Trang 18 VBT Toán 5 Cánh Diều
Hoàn thành bảng sau:
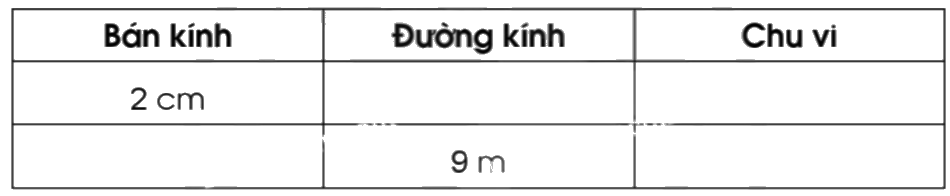
Phương pháp giải:
Muốn tính chu vi của hình tròn, ta lấy đường kính nhân với số 3,14.
Đường kính dài gấp 2 lần bán kính.
Lời giải chi tiết:

Trả lời Bài 5 Trang 20 VBT Toán 5 Cánh Diều
Thực hành: Tìm trong sân trường một cây to, đo độ dài một vòng quanh thân cây rồi ước lượng độ dài đường kính của thân cây.

- Độ dài một vòng quanh thân cây mà em đo là ................................
- Độ dài đường kính của thân cây đó ước lượng được là ..................
Phương pháp giải:
- Độ dài một vòng quanh thân cây chính là chu vi của thân cây.
- Tính đường kính của thân cây = độ dài một vòng quanh thân cây : 3,14
Lời giải chi tiết:
Ví dụ:
- Độ dài một vòng quanh thân cây mà em đo là 150 cm.
Đường kính của thân cây là:
150 : 3,14 = 47,77 (cm)
Làm tròn đến số tự nhiên ta được 48 cm.
- Vậy độ dài đường kính của thân cây đó ước lượng được là 48 cm.
Trả lời Bài 1 Trang 19 VBT Toán 5 Cánh Diều
Tính chu vi của mỗi hình tròn sau:
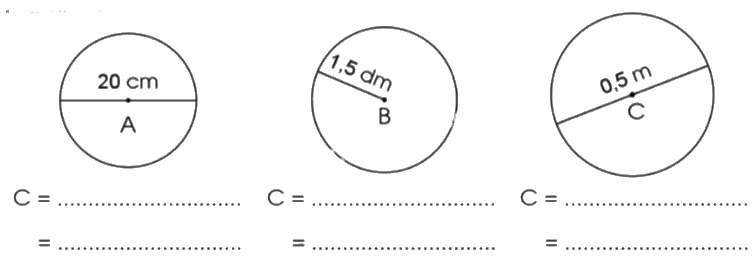
Phương pháp giải:
Muốn tính chu vi của hình tròn, ta lấy đường kính nhân với số 3,14.
Muốn tính chu vi của hình tròn, ta lấy 2 lần bán kính nhân với số 3,14.
Lời giải chi tiết:
Chu vi hình tròn tâm A là:
C = 20 x 3,14 = 62,8 (cm)
Chu vi hình tròn tâm B là:
C = 1,5 x 2 x 3,14 = 9,42 (dm)
Chu vi hình tròn tâm C là:
C = 0,5 x 3,14 = 1,7 (m)
Trả lời Bài 1 Trang 19 VBT Toán 5 Cánh Diều
Tính chu vi của mỗi hình tròn sau:
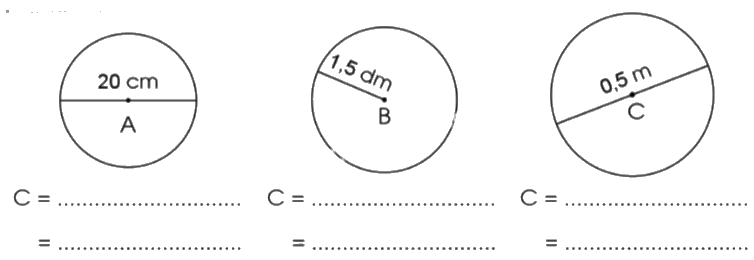
Phương pháp giải:
Muốn tính chu vi của hình tròn, ta lấy đường kính nhân với số 3,14.
Muốn tính chu vi của hình tròn, ta lấy 2 lần bán kính nhân với số 3,14.
Lời giải chi tiết:
Chu vi hình tròn tâm A là:
C = 20 x 3,14 = 62,8 (cm)
Chu vi hình tròn tâm B là:
C = 1,5 x 2 x 3,14 = 9,42 (dm)
Chu vi hình tròn tâm C là:
C = 0,5 x 3,14 = 1,7 (m)
Trả lời Bài 2 Trang 18 VBT Toán 5 Cánh Diều
Hoàn thành bảng sau:
Phương pháp giải:
Muốn tính chu vi của hình tròn, ta lấy đường kính nhân với số 3,14.
Đường kính dài gấp 2 lần bán kính.
Lời giải chi tiết:
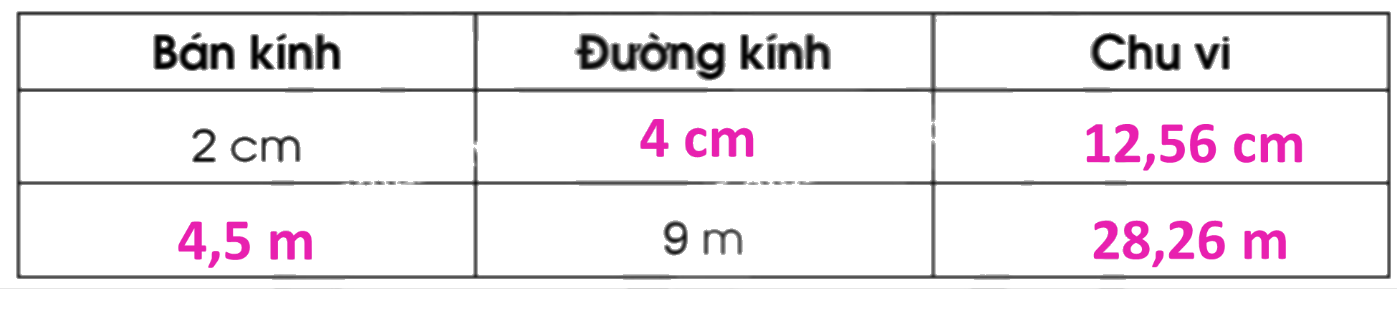
Trả lời Bài 3 Trang 19 VBT Toán 5 Cánh Diều
a) Đường kính của một bánh xe ô tô là 0,6 m. Tính chu vi bánh xe đó.
b) Bán kính của một vòng đu quay là 10 m. Nếu ngồi trên đu quay đó và quay đúng 1 vòng thì bạn đã di chuyển được bao nhiêu mét?

Phương pháp giải:
a) Muốn tính chu vi của hình tròn, ta lấy đường kính nhân với số 3,14.
b) Nếu ngồi trên đu quay đó và quay đúng 1 vòng thì quãng đường đi được chính là chu vi hình tròn.
Lời giải chi tiết:
a) Chu vi bánh xe đó là:
0,6 x 3,14 = 1,884 (m)
b) Chu vi của một vòng đu quay là:
10 x 2 x 3,14 = 62,8 (m)
Nếu ngồi trên đu quay đó và quay đúng 1 vòng thì quãng đường đi được chính là chu vi hình tròn.
Vậy bạn đã di chuyển được 62,8 m.
Trả lời Bài 4 Trang 20 VBT Toán 5 Cánh Diều
Hai con kiến bò một vòng xung quanh một hình vuông và một hình tròn như hình vẽ dưới đây. Theo em, con kiến nào đã bò được quãng đường dài hơn? Tại sao?
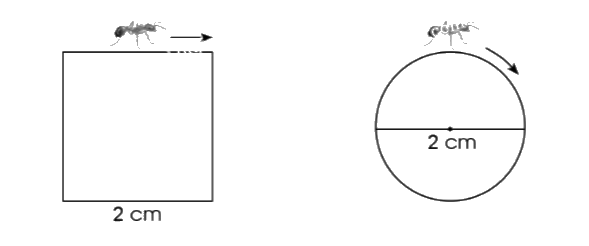
Trả lời: ...................................................................................................
Phương pháp giải:
Quãng đường 2 con kiến bò đường bằng chu vi hình vuông và chu vi hình tròn.
Lời giải chi tiết:
Quãng đường con kiến bò một vòng xung quanh một hình vuông là:
2 x 4 = 8 (cm)
Quãng đường con kiến bò một vòng xung quanh một hình tròn là:
2 x 3,14 = 6,28 (cm)
Vì 8 > 6,28 nên con kiến bò một vòng xung quanh một hình vuông đã bò được quãng đường dài hơn.
Trả lời Bài 5 Trang 20 VBT Toán 5 Cánh Diều
Thực hành: Tìm trong sân trường một cây to, đo độ dài một vòng quanh thân cây rồi ước lượng độ dài đường kính của thân cây.

- Độ dài một vòng quanh thân cây mà em đo là ................................
- Độ dài đường kính của thân cây đó ước lượng được là ..................
Phương pháp giải:
- Độ dài một vòng quanh thân cây chính là chu vi của thân cây.
- Tính đường kính của thân cây = độ dài một vòng quanh thân cây : 3,14
Lời giải chi tiết:
Ví dụ:
- Độ dài một vòng quanh thân cây mà em đo là 150 cm.
Đường kính của thân cây là:
150 : 3,14 = 47,77 (cm)
Làm tròn đến số tự nhiên ta được 48 cm.
- Vậy độ dài đường kính của thân cây đó ước lượng được là 48 cm.
Bài 55 Vở bài tập Toán 5 Cánh Diều yêu cầu học sinh vận dụng kiến thức về công thức tính chu vi hình tròn để giải các bài toán thực tế. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản sau:
Hình tròn là tập hợp tất cả các điểm nằm trên một đường tròn. Các yếu tố quan trọng của hình tròn bao gồm:
Chu vi hình tròn được tính theo công thức:
C = 2πr hoặc C = πd
Trong đó:
Để giải bài 55, chúng ta cần đọc kỹ đề bài và xác định các thông tin đã cho và yêu cầu của bài toán. Sau đó, áp dụng công thức tính chu vi hình tròn để tìm ra kết quả.
Ví dụ: Một bánh xe có đường kính 60cm. Tính chu vi của bánh xe đó.
Giải:
Chu vi của bánh xe là: C = πd = 3,14 x 60 = 188,4 (cm)
Vậy chu vi của bánh xe là 188,4cm.
Trong chương trình Toán 5, các bài tập về chu vi hình tròn thường gặp các dạng sau:
Để củng cố kiến thức về chu vi hình tròn, các em có thể luyện tập thêm các bài tập sau:
| Bài tập | Đáp án |
|---|---|
| Một hình tròn có bán kính 5cm. Tính chu vi của hình tròn đó. | 31,4cm |
| Một hình tròn có đường kính 10cm. Tính chu vi của hình tròn đó. | 31,4cm |
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài 55 Vở bài tập Toán 5 Cánh Diều và nắm vững kiến thức về chu vi hình tròn. Chúc các em học tập tốt!