Chào mừng các em học sinh đến với bài giải bài 65 Toán 5 Cánh Diều. Bài học hôm nay sẽ giúp các em nắm vững kiến thức về cách tính thể tích của hình hộp chữ nhật và hình lập phương.
Chúng ta sẽ cùng nhau đi qua từng bước giải chi tiết, kèm theo các ví dụ minh họa để các em hiểu rõ hơn về phương pháp giải bài tập này.
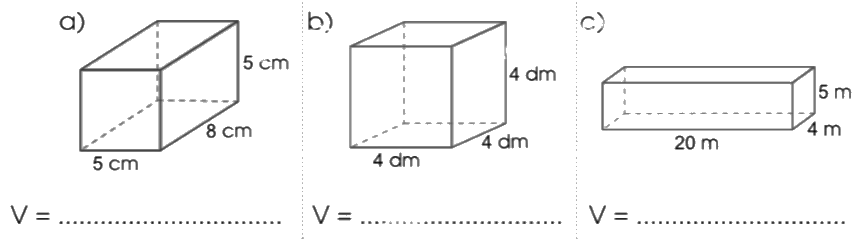
Tính thể tích các hình sau: a) Tính thể tích mỗi đồ vật sau:
Trả lời Bài 1 Trang 46 VBT Toán 5 Cánh Diều
Tính thể tích các hình sau:
Phương pháp giải:
Muốn tính thể tích hình hộp chữ nhật ta lấy chiều dài nhân với chiều rộng rồi nhân với chiều cao (cùng một đơn vị đo).
$V = a \times b \times c$
Muốn tính thể tích hình lập phương, ta lấy cạnh nhân với cạnh rồi nhân với cạnh (cùng một đơn vị đo).
$V = a \times a \times a$
Lời giải chi tiết:
a) V = $5 \times 8 \times 5 = 200$(cm3)
b) V = $4 \times 4 \times 4 = 64$(dm3)
c) V = $20 \times 4 \times 5 = 400$(m3)
Trả lời Bài 4 Trang 47 VBT Toán 5 Cánh Diều
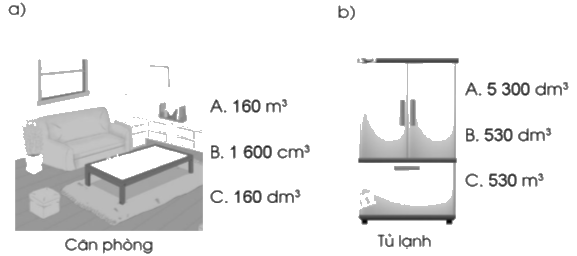
Ước lượng rồi khoanh vào chữ đứng trước số đo thể tích phù hợp:
Phương pháp giải:
Ước lượng rồi lựa chọn số đo thể tích phù hợp.
Lời giải chi tiết:
a) Căn phòng có thể tích là 160 m3.
Chọn A.
b) Tủ lạnh có thể tích là 530 dm3.
Chọn B.
Trả lời Bài 3 Trang 47 VBT Toán 5 Cánh Diều
Quan sát hình vẽ:
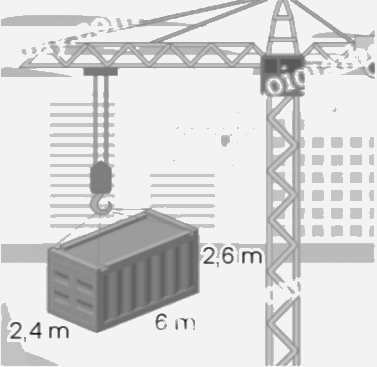
a) Tính thể tích thùng hàng.
b) Tính diện tích toàn phần của thùng hàng.
Phương pháp giải:
a) Tính thể tích thùng hàng bằng chiều dài $ \times $chiều rộng $ \times $chiều cao.
b) Tính diện tích toàn phần của thùng hàng = diện tích xung quanh + 2 $ \times $diện tích đáy
- Diện tích đáy = chiều dài $ \times $chiều rộng
- Diện tích xung quanh = chu vi đáy $ \times $chiều cao
Lời giải chi tiết:
a) Thể tích thùng hàng đó là:
$2,4 \times 6 \times 2,6 = 37,44$(m3)
Đáp số: 37,44 m3.
b) Diện tích đáy của thùng hàng là:
$2,4 \times 6 = 14,4$(m2)
Diện tích xung quanh của thùng hàng là:
$\left( {2,4 + 6} \right) \times 2 \times 2,6 = 43,68$(m2)
Diện tích toàn phần của thùng hàng là:
$43,68 + 14,4 \times 2 = 72,48$(m2)
Đáp số: 72,48 m2.
Trả lời Bài 2 Trang 46 VBT Toán 5 Cánh Diều
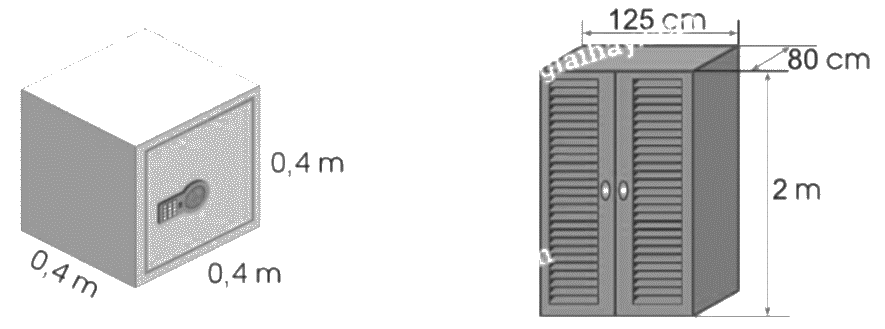
a) Tính thể tích mỗi đồ vật sau:
...................................... ....................................
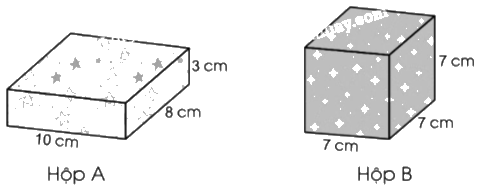
b) Trong hai hộp sau, hộp nào cần dùng nhiều giấy gói hơn?
Trả lời: .......................................................................................
Phương pháp giải:
a) Thể tích hình hộp chữ nhật: $V = a \times b \times c$
Thể tích hình lập phương: $V = a \times a \times a$
b) Tính thể tích hai hộp rồi so sánh thể tích hộp nào lớn hơn thì cần dùng nhiều giấy gói hơn.
Lời giải chi tiết:
a) Thể tích cái két sắt là:
$0,4 \times 0,4 \times 0,4 = 0,064$(m3)
Đổi: 125 cm = 1,25 m; 80 cm = 0,8 m.
Thể tích cái tủ gỗ là:
$1,25 \times 0,8 \times 2 = 2$(m3)
b) Thể tích hộp A là:
$10 \times 8 \times 3 = 240$(cm3)
Thể tích hộp B là:
$7 \times 7 \times 7 = 343$(cm3)
Vì 343 cm3 > 240 cm3 nên Thể tích hộp B > Thể tích hộp A.
Vậy hộp B cần dùng nhiều giấy gói hơn.
Trả lời Bài 1 Trang 46 VBT Toán 5 Cánh Diều
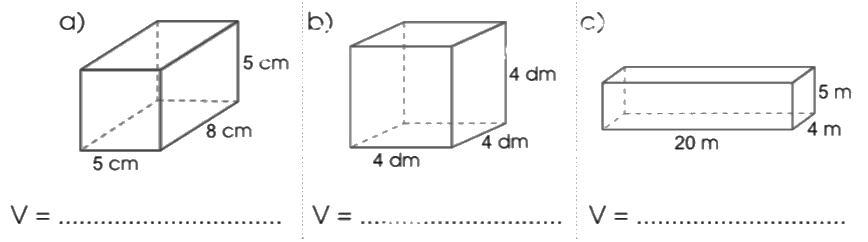
Tính thể tích các hình sau:
Phương pháp giải:
Muốn tính thể tích hình hộp chữ nhật ta lấy chiều dài nhân với chiều rộng rồi nhân với chiều cao (cùng một đơn vị đo).
$V = a \times b \times c$
Muốn tính thể tích hình lập phương, ta lấy cạnh nhân với cạnh rồi nhân với cạnh (cùng một đơn vị đo).
$V = a \times a \times a$
Lời giải chi tiết:
a) V = $5 \times 8 \times 5 = 200$(cm3)
b) V = $4 \times 4 \times 4 = 64$(dm3)
c) V = $20 \times 4 \times 5 = 400$(m3)
Trả lời Bài 2 Trang 46 VBT Toán 5 Cánh Diều
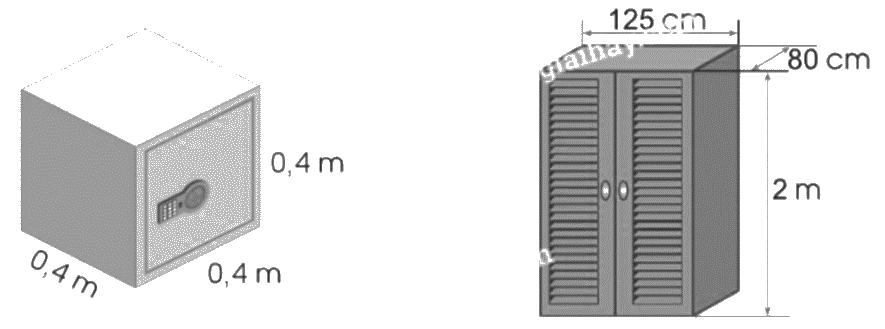
a) Tính thể tích mỗi đồ vật sau:
...................................... ....................................
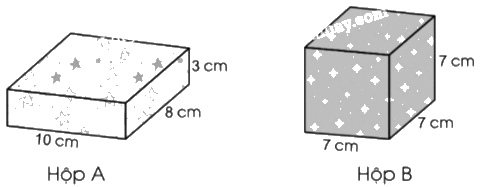
b) Trong hai hộp sau, hộp nào cần dùng nhiều giấy gói hơn?
Trả lời: .......................................................................................
Phương pháp giải:
a) Thể tích hình hộp chữ nhật: $V = a \times b \times c$
Thể tích hình lập phương: $V = a \times a \times a$
b) Tính thể tích hai hộp rồi so sánh thể tích hộp nào lớn hơn thì cần dùng nhiều giấy gói hơn.
Lời giải chi tiết:
a) Thể tích cái két sắt là:
$0,4 \times 0,4 \times 0,4 = 0,064$(m3)
Đổi: 125 cm = 1,25 m; 80 cm = 0,8 m.
Thể tích cái tủ gỗ là:
$1,25 \times 0,8 \times 2 = 2$(m3)
b) Thể tích hộp A là:
$10 \times 8 \times 3 = 240$(cm3)
Thể tích hộp B là:
$7 \times 7 \times 7 = 343$(cm3)
Vì 343 cm3 > 240 cm3 nên Thể tích hộp B > Thể tích hộp A.
Vậy hộp B cần dùng nhiều giấy gói hơn.
Trả lời Bài 3 Trang 47 VBT Toán 5 Cánh Diều
Quan sát hình vẽ:
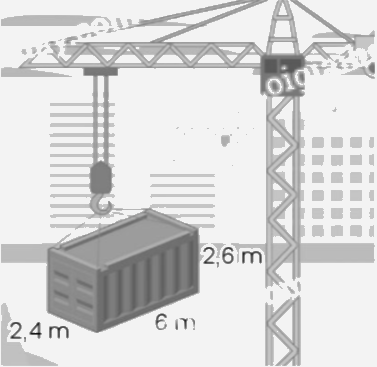
a) Tính thể tích thùng hàng.
b) Tính diện tích toàn phần của thùng hàng.
Phương pháp giải:
a) Tính thể tích thùng hàng bằng chiều dài $ \times $chiều rộng $ \times $chiều cao.
b) Tính diện tích toàn phần của thùng hàng = diện tích xung quanh + 2 $ \times $diện tích đáy
- Diện tích đáy = chiều dài $ \times $chiều rộng
- Diện tích xung quanh = chu vi đáy $ \times $chiều cao
Lời giải chi tiết:
a) Thể tích thùng hàng đó là:
$2,4 \times 6 \times 2,6 = 37,44$(m3)
Đáp số: 37,44 m3.
b) Diện tích đáy của thùng hàng là:
$2,4 \times 6 = 14,4$(m2)
Diện tích xung quanh của thùng hàng là:
$\left( {2,4 + 6} \right) \times 2 \times 2,6 = 43,68$(m2)
Diện tích toàn phần của thùng hàng là:
$43,68 + 14,4 \times 2 = 72,48$(m2)
Đáp số: 72,48 m2.
Trả lời Bài 4 Trang 47 VBT Toán 5 Cánh Diều
Ước lượng rồi khoanh vào chữ đứng trước số đo thể tích phù hợp:
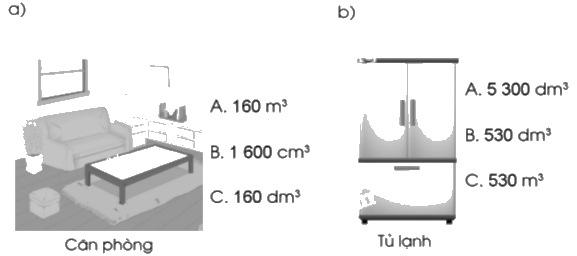
Phương pháp giải:
Ước lượng rồi lựa chọn số đo thể tích phù hợp.
Lời giải chi tiết:
a) Căn phòng có thể tích là 160 m3.
Chọn A.
b) Tủ lạnh có thể tích là 530 dm3.
Chọn B.
Bài 65 Vở bài tập Toán 5 Cánh Diều yêu cầu học sinh vận dụng kiến thức về thể tích hình hộp chữ nhật và hình lập phương để giải các bài toán thực tế. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm và công thức sau:
Bài 1: Một hình hộp chữ nhật có chiều dài 5cm, chiều rộng 4cm và chiều cao 3cm. Tính thể tích của hình hộp chữ nhật đó.
Giải:
Thể tích của hình hộp chữ nhật là: V = 5cm x 4cm x 3cm = 60cm3
Bài 2: Một hình lập phương có cạnh 2cm. Tính thể tích của hình lập phương đó.
Giải:
Thể tích của hình lập phương là: V = 2cm x 2cm x 2cm = 8cm3
Ngoài việc tính thể tích của hình hộp chữ nhật và hình lập phương, chúng ta còn có thể áp dụng kiến thức này để giải các bài toán liên quan đến đo lường và tính toán trong thực tế. Ví dụ, tính lượng nước cần để đổ đầy một bể nước hình hộp chữ nhật, hoặc tính lượng đất cần để lấp đầy một thùng chứa hình lập phương.
Hy vọng với bài giải chi tiết này, các em học sinh sẽ hiểu rõ hơn về cách tính thể tích của hình hộp chữ nhật và hình lập phương, từ đó có thể tự tin giải các bài tập tương tự. Chúc các em học tốt!
| Hình dạng | Công thức tính thể tích |
|---|---|
| Hình hộp chữ nhật | V = a x b x c |
| Hình lập phương | V = a x a x a |
| Trong đó: a, b, c là chiều dài, chiều rộng, chiều cao; a là cạnh của hình lập phương. | |