Bài học hôm nay, các em học sinh lớp 4 sẽ cùng nhau khám phá phương pháp rút gọn phân số. Đây là một kỹ năng quan trọng trong chương trình Toán học, giúp các em biểu diễn phân số một cách đơn giản nhất.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong SGK Toán lớp 4 Chân trời sáng tạo, giúp các em nắm vững kiến thức và tự tin giải bài tập.
Rút gọn các phân số chưa tối giản. Phân số nào dưới đây bằng 6/8
Video hướng dẫn giải
Phân số nào dưới đây bằng $\frac{6}{8}$?
$\frac{3}{4}$ ; $\frac{8}{6}$ ; $\frac{{15}}{{60}}$ ; $\frac{{42}}{{56}}$
Phương pháp giải:
- Rút gọn các phân số thành phân số tối giản
- Kết luận các phân số bằng $\frac{6}{8}$
Lời giải chi tiết:
Ta có: $\frac{6}{8} = \frac{{6:2}}{{8:2}} = \frac{3}{4}$
$\frac{{15}}{{60}} = \frac{{15:15}}{{60:15}} = \frac{1}{4}$
$\frac{{42}}{{56}} = \frac{{42:14}}{{56:14}} = \frac{3}{4}$
Vậy phân số $\frac{3}{4}$ , $\frac{{42}}{{56}}$ bằng $\frac{6}{8}$
>> Xem chi tiết: Lý thuyết: Bài 63. Rút gọn phân số
Video hướng dẫn giải
Rút gọn các phân số chưa tối giản.
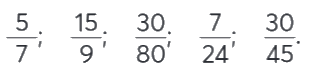
Phương pháp giải:
- Xem tử số và mẫu số có cùng chia hết cho số tự nhiên nào lớn hơn 1
- Chia tử số và mẫu số cho số đó
Cứ làm như thế cho đến khi nhận được phân số tối giản
Lời giải chi tiết:
$\frac{{15}}{9} = \frac{{15:3}}{{9:3}} = \frac{5}{3}$
$\frac{{30}}{{80}} = \frac{{30:10}}{{80:10}} = \frac{3}{8}$
$\frac{{30}}{{45}} = \frac{{30:15}}{{45:15}} = \frac{2}{3}$
Video hướng dẫn giải
Rút gọn các phân số.

Phương pháp giải:
Rút gọn phân số:
- Xem tử số và mẫu số có cùng chia hết cho số tự nhiên nào lớn hơn 1
- Chia tử số và mẫu số cho số đó
Cứ làm như thế cho đến khi nhận được phân số tối giản
Lời giải chi tiết:
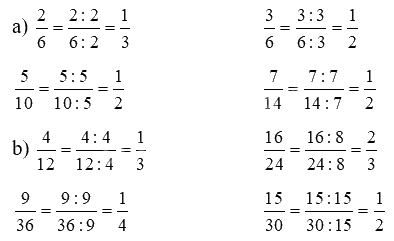
Video hướng dẫn giải
Rút gọn các phân số.

Phương pháp giải:
- Xem tử số và mẫu số có cùng chia hết cho số tự nhiên nào lớn hơn 1
- Chia tử số và mẫu số cho số đó
Cứ làm như thế cho đến khi nhận được phân số tối giản
Lời giải chi tiết:

Video hướng dẫn giải
Số?

$\frac{{..?..}}{{..?..}}$ số quả măng cụt nằm trên đĩa.
Phương pháp giải:
Viết phân số có tử số là số quả măng cụt nằm trên đĩa và mẫu số là số quả măng cụt có tất cả
Lời giải chi tiết:
Trong hình vẽ có 9 quả măng cụt và có 6 quả măng cụt nằm trên đĩa.
Vậy $\frac{6}{9}$ (hoặc $\frac{2}{3}$) số quả măng cụt nằm trên đĩa.
Video hướng dẫn giải
Việt Nam có 63 tỉnh, thành phố, trong đó có 28 tỉnh và thành phố có biển.
- Viết phân số dạng tối giản chỉ số tỉnh và thành phố có biển trên cả nước.
- Em kể tên một vài tỉnh, thành phố có biển ở nước ta mà em biết.

Phương pháp giải:
- Phân số chỉ số tỉnh và thành phố có biển trên cả nước có tử số là số tỉnh (thành phố) có biển và mẫu số là số tỉnh của Việt Nam
- Rút gọn phân số
Lời giải chi tiết:
Ta có $\frac{{28}}{{63}} = \frac{4}{9}$
Vậy phân số dạng tối giản chỉ số tỉnh và thành phố có biển trên cả nước là $\frac{4}{9}$
Một số tỉnh, thành phố có biển ở nước ta là: Thanh Hóa, Nghệ An, Đà Nẵng, ….
Video hướng dẫn giải
Rút gọn các phân số.

Phương pháp giải:
Rút gọn phân số:
- Xem tử số và mẫu số có cùng chia hết cho số tự nhiên nào lớn hơn 1
- Chia tử số và mẫu số cho số đó
Cứ làm như thế cho đến khi nhận được phân số tối giản
Lời giải chi tiết:
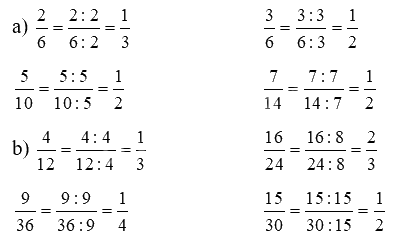
Video hướng dẫn giải
Rút gọn các phân số.

Phương pháp giải:
- Xem tử số và mẫu số có cùng chia hết cho số tự nhiên nào lớn hơn 1
- Chia tử số và mẫu số cho số đó
Cứ làm như thế cho đến khi nhận được phân số tối giản
Lời giải chi tiết:

Video hướng dẫn giải
Rút gọn các phân số chưa tối giản.
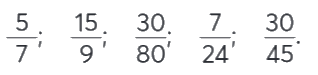
Phương pháp giải:
- Xem tử số và mẫu số có cùng chia hết cho số tự nhiên nào lớn hơn 1
- Chia tử số và mẫu số cho số đó
Cứ làm như thế cho đến khi nhận được phân số tối giản
Lời giải chi tiết:
$\frac{{15}}{9} = \frac{{15:3}}{{9:3}} = \frac{5}{3}$
$\frac{{30}}{{80}} = \frac{{30:10}}{{80:10}} = \frac{3}{8}$
$\frac{{30}}{{45}} = \frac{{30:15}}{{45:15}} = \frac{2}{3}$
Video hướng dẫn giải
Phân số nào dưới đây bằng $\frac{6}{8}$?
$\frac{3}{4}$ ; $\frac{8}{6}$ ; $\frac{{15}}{{60}}$ ; $\frac{{42}}{{56}}$
Phương pháp giải:
- Rút gọn các phân số thành phân số tối giản
- Kết luận các phân số bằng $\frac{6}{8}$
Lời giải chi tiết:
Ta có: $\frac{6}{8} = \frac{{6:2}}{{8:2}} = \frac{3}{4}$
$\frac{{15}}{{60}} = \frac{{15:15}}{{60:15}} = \frac{1}{4}$
$\frac{{42}}{{56}} = \frac{{42:14}}{{56:14}} = \frac{3}{4}$
Vậy phân số $\frac{3}{4}$ , $\frac{{42}}{{56}}$ bằng $\frac{6}{8}$
Video hướng dẫn giải
Số?

$\frac{{..?..}}{{..?..}}$ số quả măng cụt nằm trên đĩa.
Phương pháp giải:
Viết phân số có tử số là số quả măng cụt nằm trên đĩa và mẫu số là số quả măng cụt có tất cả
Lời giải chi tiết:
Trong hình vẽ có 9 quả măng cụt và có 6 quả măng cụt nằm trên đĩa.
Vậy $\frac{6}{9}$ (hoặc $\frac{2}{3}$) số quả măng cụt nằm trên đĩa.
Video hướng dẫn giải
Việt Nam có 63 tỉnh, thành phố, trong đó có 28 tỉnh và thành phố có biển.
- Viết phân số dạng tối giản chỉ số tỉnh và thành phố có biển trên cả nước.
- Em kể tên một vài tỉnh, thành phố có biển ở nước ta mà em biết.

Phương pháp giải:
- Phân số chỉ số tỉnh và thành phố có biển trên cả nước có tử số là số tỉnh (thành phố) có biển và mẫu số là số tỉnh của Việt Nam
- Rút gọn phân số
Lời giải chi tiết:
Ta có $\frac{{28}}{{63}} = \frac{4}{9}$
Vậy phân số dạng tối giản chỉ số tỉnh và thành phố có biển trên cả nước là $\frac{4}{9}$
Một số tỉnh, thành phố có biển ở nước ta là: Thanh Hóa, Nghệ An, Đà Nẵng, ….
>> Xem chi tiết: Lý thuyết: Bài 63. Rút gọn phân số
Bài 63 Toán lớp 4 trang 49 thuộc chương trình Toán 4 Chân trời sáng tạo, tập trung vào việc rèn luyện kỹ năng rút gọn phân số. Việc nắm vững kiến thức này là nền tảng quan trọng cho các phép toán về phân số phức tạp hơn trong các lớp học tiếp theo.
Rút gọn phân số là việc chia cả tử số và mẫu số của phân số cho một ước chung lớn hơn 1. Mục đích của việc rút gọn là để biểu diễn phân số ở dạng đơn giản nhất, tức là tử số và mẫu số không còn ước chung nào khác ngoài 1.
Ví dụ 1: Rút gọn phân số 12/18
Ví dụ 2: Rút gọn phân số 25/35
Hãy tự rút gọn các phân số sau:
Khi rút gọn phân số, cần tìm ƯCLN của tử số và mẫu số để đảm bảo phân số được rút gọn về dạng đơn giản nhất. Nếu không tìm được ƯCLN, có thể chia cả tử số và mẫu số cho một ước chung bất kỳ, nhưng việc này có thể cần thực hiện nhiều lần để đạt được kết quả cuối cùng.
Phân số tối giản là phân số mà tử số và mẫu số không còn ước chung nào khác ngoài 1. Việc rút gọn phân số giúp chúng ta chuyển đổi một phân số bất kỳ thành phân số tối giản.
Rút gọn phân số có nhiều ứng dụng trong thực tế, chẳng hạn như:
Hy vọng với bài viết này, các em học sinh lớp 4 đã hiểu rõ hơn về cách rút gọn phân số và có thể áp dụng kiến thức này vào việc giải các bài tập Toán học một cách hiệu quả. Hãy luyện tập thường xuyên để nắm vững kỹ năng này nhé!