Chào mừng các em học sinh đến với bài trắc nghiệm Bài 2: Tia phân giác của một góc môn Toán lớp 7 chương trình Cánh diều. Bài trắc nghiệm này được thiết kế để giúp các em ôn tập và củng cố kiến thức đã học về tia phân giác, các tính chất và ứng dụng của nó.
Giaitoan.edu.vn cung cấp bộ đề trắc nghiệm đa dạng, từ dễ đến khó, kèm theo đáp án chi tiết và lời giải thích rõ ràng. Hãy cùng thử sức để đánh giá năng lực của bản thân nhé!
Chọn phát biểu sai trong các phát biểu sau:
Nếu tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì tia \(Ot\) nằm giữa hai tia \(Ox;Oy.\)
Nếu tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)
Nếu \(\widehat {xOt} = \widehat {yOt}\) thì tia \(Ot\) là tia phân giác của \(\widehat {xOy}\).
Nếu \(\widehat {xOt} = \widehat {yOt}\) và tia \(Ot\) nằm giữa hai tia \(Ox;Oy\) thì tia \(Ot\) là tia phân giác của \(\widehat {xOy}\).
Cho $Ot$ là tia phân giác của \(\widehat {xOy}\). Biết \(\widehat {xOy} = {100^0}\), số đo của \(\widehat {xOt}\) là:
\({40^0}\)
\({60^0}\)
\({50^0}\)
\({200^0}\)
Cho \(\widehat {xOy}\) là góc vuông có tia On là phân giác, số đo của \(\widehat {xOn}\) là:
\({40^0}\)
\({90^0}\)
\({45^0}\)
\({85^0}\)
Cho tia \(On\) là tia phân giác của \(\widehat {mOt}\). Biết \(\widehat {mOn} = {70^0}\), số đo của \(\widehat {mOt}\) là:
\({140^0}\)
\({120^0}\)
\({35^0}\)
\({60^0}\)
Cho \(\widehat {AOB} = 90^\circ \) và tia \(OB\) là tia phân giác của góc \(AOC.\) Khi đó góc \(AOC\) là
Góc vuông
Góc nhọn
Góc tù
Góc bẹt
Cho \(\widehat {AOC} = {60^0}\). Vẽ tia \(OB\) sao cho \(OA\) là tia phân giác của \(\widehat {BOC}\). Tính số đo của \(\widehat {AOB}\) và \(\widehat {BOC}\).
\(\widehat {AOB} = 70^\circ ;\,\widehat {BOC} = 140^\circ \)
\(\widehat {AOB} = 90^\circ ;\,\widehat {BOC} = 120^\circ \)
\(\widehat {AOB} = 120^\circ ;\,\widehat {BOC} = 60^\circ \)
\(\widehat {AOB} = 60^\circ ;\,\widehat {BOC} = 120^\circ \)
Cho \(\widehat {AOB} = {110^0}\) và \(\widehat {AOC} = {55^0}\) sao cho \(\widehat {AOB}\) và \(\widehat {AOC}\) không kề nhau. Chọn câu sai.
Tia \(OC\) nằm giữa hai tia \(OA\) và \(OB.\)
Tia \(OC\) là tia phân giác góc \(AOB.\)
\(\widehat {BOC} = 65^\circ \)
\(\widehat {BOC} = 55^\circ \)
Cho \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù. Biết \(\widehat {xOy} = 120^\circ \) và tia \(Ot\) là tia phân giác của \(\widehat {yOz}.\) Tính số đo góc \(xOt.\)
\({140^0}\)
\({150^0}\)
\({90^0}\)
\({120^0}\)
Cho góc \(AOB\) và tia phân giác \(OC\) của góc đó. Vẽ tia phân giác \(OM\) của góc \(BOC.\) Biết \(\widehat {BOM} = 35^\circ .\) Tính số đo góc \(AOB.\)
\({150^0}\)
\({120^0}\)
\({140^0}\)
\({160^0}\)
Cho góc bẹt \(xOy\). Trên cùng một nửa mặt phẳng bờ \(xy\) vẽ các tia \(Om;On\) sao cho \(\widehat {xOm} = a^\circ \,\left( {a < 180} \right)\) và \(\widehat {yOn} = 70^\circ .\) Với giá trị nào của \(a\) thì tia \(On\) là tia phân giác của \(\widehat {yOm}\).
\({45^0}\)
\({30^0}\)
\({50^0}\)
\({40^0}\)
Cho hai góc kề bù \(\widehat {xOy};\,\widehat {xOz}\). Vẽ tia \(Ot\) là phân giác \(\widehat {xOy}\) và tia \(Ot'\) là phân giác \(\widehat {xOz}\). Tính \(\widehat {tOt'}\).
\({70^0}\)
\({80^0}\)
\({60^0}\)
\({90^0}\)
Cho \(\widehat {AOB},\;\widehat {AOC}\) kề với nhau. Biết \(\widehat {AOB} = \widehat {AOC} = {65^0}\),
Chọn câu đúng.
Tia \(OB\) là tia phân giác của \(\widehat {AOC}\).
Tia \(OC\) là tia phân giác của \(\widehat {BOA}\).
Tia \(OA\) là tia phân giác của \(\widehat {BOC}\).
Không có tia nào là tia phân giác của góc.
Số đo góc \(BOC\) là
\({140^0}\)
\({120^0}\)
\({35^0}\)
\({130^0}\)
Cho hai góc kề bù \(\widehat {xOy}\) và \(\widehat {yOz}\) sao cho \(\widehat {xOy} = {120^0}\). Gọi Ot là tia phân giác của \(\widehat {xOy}\), vẽ tia Om trong góc \(\widehat {yOz}\) sao cho \(\widehat {tOm} = {90^0}\).
Tính \(\widehat {yOm}\).
\({30^0}\)
\({40^0}\)
\({35^0}\)
\({60^0}\)
Tia \(Om\) là tia phân giác của góc nào?
Tia \(Om\) là tia phân giác của \(\widehat {xOz}\)
Tia \(Om\) là tia phân giác của \(\widehat {mOz}\)
Tia \(Om\) là tia phân giác của \(\widehat {tOz}\)
Tia \(Om\) là tia phân giác của \(\widehat {yOz}\)
Cho góc \(xOy\) bằng \(110^\circ \) có tia \(Oz\) là tia phân giác. Vẽ các tia \(Om;On\) nằm trong góc \(xOy\) sao cho \(\widehat {xOm} = \widehat {yOn} = 30^\circ \).
Tính góc \(zOn\).
\({40^0}\)
\({30^0}\)
\({25^0}\)
\({60^0}\)
Chọn câu đúng.
Tia \(Oz\) là tia phân giác của \(\widehat {xOn}\).
Tia \(Oz\) là tia phân giác của \(\widehat {mOn}\).
Tia \(Oz\) là tia phân giác của \(\widehat {mOy}\).
Tia \(Oz\) là tia phân giác của \(\widehat {xOz}\).
Hai đường thẳng \(MN\) và \(PQ\) cắt nhau tại \(O\), tạo thành \(\widehat {MOP} = 50^\circ \) . Cho tia OK là tia phân giác của \(\widehat {PON}\). Chọn khẳng định sai.
\(\widehat {MOQ} = \widehat {PON} = {130^o}\)
\(\widehat {POK} = \widehat {NOK} = 50^\circ \)
\(\widehat {MOQ} + \widehat {QON} = {180^o}\)
\(\widehat {QON} = 50^\circ \)
Hai đường thẳng \(xy\) và \(x'y'\) cắt nhau tại \(O.\) Biết \(\widehat {xOx'} = {70^o}\). \(Ot\) là tia phân giác của góc xOx’. \(Ot'\) là tia đối của tia \(Ot.\) Tính số đo góc \(yOt'.\)
\(\widehat {yOt'} = {35^o}\)
\(\widehat {yOt'} = {70^o}\)
\(\widehat {yOt'} = {145^o}\)
\(\widehat {yOt'} = {110^o}\)
Cho \(\widehat {xOy},\widehat {yOz}\) là 2 góc kề bù. Góc xOy có số đo là 60o . Kẻ Om và On lần lượt là tia phân giác của 2 góc đó. Tính số đo góc mOn
30o
60o
120o
90o
Hai đường thẳng \(AB\) và \(CD\) cắt nhau tại \(O\). Biết \(\widehat {AOD} - \widehat {AOC} = 60^\circ \) . Gọi \(OM\) là phân giác \(\widehat {AOC}\) và \(ON\) là tia đối của tia \(OM\). Tính \(\widehat {BON}\) và \(\widehat {DON}.\)
\(\widehat {BON} = \widehat {DON} = 25^\circ \)
\(\widehat {BON} = \widehat {DON} = 30^\circ \)
\(\widehat {BON} = \widehat {DON} = 60^\circ \)
\(\widehat {BON} = \widehat {DON} = 45^\circ \)
Lời giải và đáp án
Chọn phát biểu sai trong các phát biểu sau:
Nếu tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì tia \(Ot\) nằm giữa hai tia \(Ox;Oy.\)
Nếu tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)
Nếu \(\widehat {xOt} = \widehat {yOt}\) thì tia \(Ot\) là tia phân giác của \(\widehat {xOy}\).
Nếu \(\widehat {xOt} = \widehat {yOt}\) và tia \(Ot\) nằm giữa hai tia \(Ox;Oy\) thì tia \(Ot\) là tia phân giác của \(\widehat {xOy}\).
Đáp án : C
Nếu \(\widehat {xOt} = \widehat {yOt}\) và tia \(Ot\) nằm giữa hai tia \(Ox;Oy\) thì tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) nên C sai, D đúng.
Cho $Ot$ là tia phân giác của \(\widehat {xOy}\). Biết \(\widehat {xOy} = {100^0}\), số đo của \(\widehat {xOt}\) là:
\({40^0}\)
\({60^0}\)
\({50^0}\)
\({200^0}\)
Đáp án : C
Nếu tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)
Vì tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2} = \dfrac{{100^\circ }}{2} = 50^\circ \)
Cho \(\widehat {xOy}\) là góc vuông có tia On là phân giác, số đo của \(\widehat {xOn}\) là:
\({40^0}\)
\({90^0}\)
\({45^0}\)
\({85^0}\)
Đáp án : C
+ Góc vuông là góc có số đo bằng \(90^\circ \)
+ Sử dụng: Nếu tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)
Vì \(On\) là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOn} = \widehat {nOy} = \dfrac{{\widehat {xOy}}}{2} = \dfrac{{90^\circ }}{2} = 45^\circ \)
Cho tia \(On\) là tia phân giác của \(\widehat {mOt}\). Biết \(\widehat {mOn} = {70^0}\), số đo của \(\widehat {mOt}\) là:
\({140^0}\)
\({120^0}\)
\({35^0}\)
\({60^0}\)
Đáp án : A
Sử dụng: Nếu tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)
Vì tia \(On\) là tia phân giác của \(\widehat {mOt}\) nên \(\widehat {mOn} = \widehat {nOt} = \dfrac{{\widehat {mOt}}}{2}\)
\( \Rightarrow \widehat {mOt} = 2.\widehat {mOn} = 2.70^\circ = 140^\circ \).
Cho \(\widehat {AOB} = 90^\circ \) và tia \(OB\) là tia phân giác của góc \(AOC.\) Khi đó góc \(AOC\) là
Góc vuông
Góc nhọn
Góc tù
Góc bẹt
Đáp án : D
Sử dụng: Nếu tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)
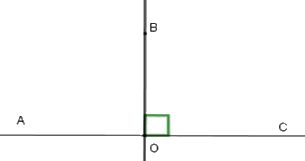
Vì tia \(OB\) là tia phân giác của góc \(AOC\) nên \(\widehat {AOB} = \widehat {BOC} = \dfrac{{\widehat {AOC}}}{2}\)
Do đó \(\widehat {AOC} = 2.\widehat {AOB} = 2.90^\circ = 180^\circ \)
Nên góc \(AOC\) là góc bẹt.
Cho \(\widehat {AOC} = {60^0}\). Vẽ tia \(OB\) sao cho \(OA\) là tia phân giác của \(\widehat {BOC}\). Tính số đo của \(\widehat {AOB}\) và \(\widehat {BOC}\).
\(\widehat {AOB} = 70^\circ ;\,\widehat {BOC} = 140^\circ \)
\(\widehat {AOB} = 90^\circ ;\,\widehat {BOC} = 120^\circ \)
\(\widehat {AOB} = 120^\circ ;\,\widehat {BOC} = 60^\circ \)
\(\widehat {AOB} = 60^\circ ;\,\widehat {BOC} = 120^\circ \)
Đáp án : D
Sử dụng: Nếu tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)
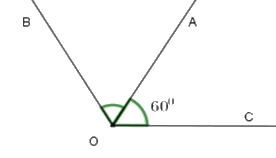
Vì tia \(OA\) là tia phân giác của \(\widehat {BOC}\) nên ta có
\(\widehat {AOB} = \widehat {AOC} = \dfrac{{\widehat {BOC}}}{2}\) nên \(\widehat {AOB} = 60^\circ ;\,\widehat {BOC} = 2.\widehat {AOC} = 2.60^\circ = 120^\circ \)
Vậy \(\widehat {AOB} = 60^\circ ;\,\widehat {BOC} = 120^\circ \).
Cho \(\widehat {AOB} = {110^0}\) và \(\widehat {AOC} = {55^0}\) sao cho \(\widehat {AOB}\) và \(\widehat {AOC}\) không kề nhau. Chọn câu sai.
Tia \(OC\) nằm giữa hai tia \(OA\) và \(OB.\)
Tia \(OC\) là tia phân giác góc \(AOB.\)
\(\widehat {BOC} = 65^\circ \)
\(\widehat {BOC} = 55^\circ \)
Đáp án : C
+ Sử dụng dấu hiệu nhận biết tia nằm giữa hai tia
+ Tính góc \(BOC\)
+ Sử dụng định nghĩa tia phân giác
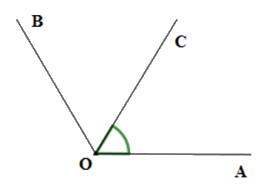
Vì \(\widehat {AOB}\) và \(\widehat {AOC}\) không kề nhau nên hai tia \(OC;OB\) thuộc cùng nửa mặt phẳng bờ là đường thẳng chứa tia \(OA\). Lại có \(\widehat {AOC} < \widehat {AOB}\,\left( {55^\circ < 110^\circ } \right)\) nên tia \(OC\) nằm giữa hai tia \(OA\) và \(OB.\) (1)
Từ đó \(\widehat {AOC} + \widehat {COB} = \widehat {AOB}\,\) hay \(\widehat {COB} = \widehat {AOB} - \widehat {AOC} = 110^\circ - 55^\circ = 55^\circ \)
Suy ra \(\widehat {AOC} = \widehat {BOC} = 55^\circ \) (2)
Từ (1) và (2) suy ra tia \(OC\) là tia phân giác góc \(AOB.\)
Vậy A, B, D đúng và C sai.
Cho \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù. Biết \(\widehat {xOy} = 120^\circ \) và tia \(Ot\) là tia phân giác của \(\widehat {yOz}.\) Tính số đo góc \(xOt.\)
\({140^0}\)
\({150^0}\)
\({90^0}\)
\({120^0}\)
Đáp án : B
+ Sử dụng: Hai góc kề bù có tổng số đo bằng \(180^\circ \) và tính chất tia phân giác của một góc để tính toán.
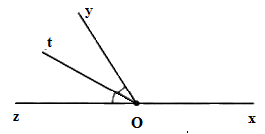
Vì \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù nên \(\widehat {xOy} + \widehat {yOz} = 180^\circ \) mà \(\widehat {xOy} = 120^\circ \) nên \(\widehat {yOz} = 180^\circ - 120^\circ = 60^\circ \).
Lại có tia \(Ot\) là tia phân giác của \(\widehat {yOz}\) nên \(\widehat {zOt} = \dfrac{1}{2}\widehat {yOz} = \dfrac{1}{2}.60^\circ = 30^\circ \)
Lại có \(\widehat {zOt};\,\widehat {tOx}\) là hai góc kề bù nên \(\widehat {zOt} + \widehat {tOx} = 180^\circ \Rightarrow \widehat {tOx} = 180^\circ - \widehat {zOt}\)\( = 180^\circ - 30^\circ = 150^\circ .\)
Vậy \(\widehat {tOx} = 150^\circ .\)
Cho góc \(AOB\) và tia phân giác \(OC\) của góc đó. Vẽ tia phân giác \(OM\) của góc \(BOC.\) Biết \(\widehat {BOM} = 35^\circ .\) Tính số đo góc \(AOB.\)
\({150^0}\)
\({120^0}\)
\({140^0}\)
\({160^0}\)
Đáp án : C
Sử dụng: Nếu tia \(Ot\) là tiam phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)
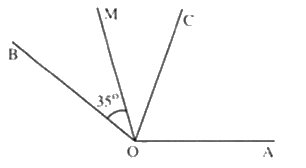
Vì tia \(OM\) là tia phân của góc \(BOC\)
nên \(\widehat {BOC} = 2.\widehat {BOM} = 2.35^\circ = 70^\circ \)
Lại có tia \(OC\) là tia phân giác của \(\widehat {AOB}\) nên \(\widehat {AOB} = 2.\widehat {BOC} = 2.70^\circ = 140^\circ \). Vậy \(\widehat {AOB} = 140^\circ \).
Cho góc bẹt \(xOy\). Trên cùng một nửa mặt phẳng bờ \(xy\) vẽ các tia \(Om;On\) sao cho \(\widehat {xOm} = a^\circ \,\left( {a < 180} \right)\) và \(\widehat {yOn} = 70^\circ .\) Với giá trị nào của \(a\) thì tia \(On\) là tia phân giác của \(\widehat {yOm}\).
\({45^0}\)
\({30^0}\)
\({50^0}\)
\({40^0}\)
Đáp án : D
Sử dụng tính chất tia phân giác và tính chất hai góc kề bù.
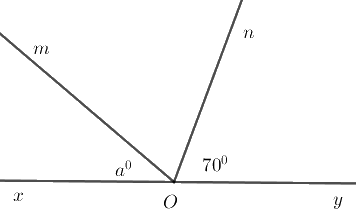
Giả sử tia \(On\) là tia phân giác của góc \(yOm\) thì \(\widehat {mOy} = 2.\widehat {yOn} = 2.70^\circ = 140^\circ \).
Mà hai góc \(\widehat {xOm};\widehat {yOm}\) là hai góc kề bù nên \(\widehat {xOm} + \widehat {yOm} = 180^\circ \)\( \Rightarrow \widehat {xOm} = 180^\circ - \widehat {yOm}\) \( = 180^\circ - 140^\circ = 40^\circ \).
Vậy \(a = 40 ^\circ\).
Cho hai góc kề bù \(\widehat {xOy};\,\widehat {xOz}\). Vẽ tia \(Ot\) là phân giác \(\widehat {xOy}\) và tia \(Ot'\) là phân giác \(\widehat {xOz}\). Tính \(\widehat {tOt'}\).
\({70^0}\)
\({80^0}\)
\({60^0}\)
\({90^0}\)
Đáp án : D
+ Sử dụng tính chất hai góc kề bù và tính chất tia phân giác của một góc để tính toán
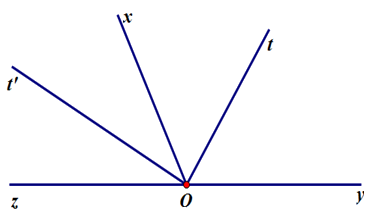
Vì tia \(Ot\) là phân giác \(\widehat {xOy}\) nên \(\widehat {yOt} = \widehat {xOt} = \dfrac{1}{2}\widehat {xOy}\) suy ra \(\widehat {xOy} = 2.\widehat {tOx}\) (1)
Và tia \(Ot'\) là phân giác \(\widehat {yOz}\) nên \(\widehat {zOt'} = \widehat {xOt'} = \dfrac{1}{2}\widehat {xOz}\) suy ra \(\widehat {xOz} = 2.\widehat {t'Ox}\) (2)
Mà \(\widehat {xOy};\,\widehat {xOz}\) là hai góc kề bù nên \(\widehat {xOy} + \widehat {xOz} = 180^\circ \) (3)
Từ (1) (2) (3) suy ra \(2.\widehat {tOx} + 2.\widehat {t'Ox} = 180^\circ \) suy ra \(2.\left( {\widehat {tOx} + \widehat {t'Ox}} \right) = 180^\circ \Rightarrow \widehat {tOx} + \widehat {t'Ox} = 90^\circ \) (4)
Lại có tia \(Ot\) nằm giữa hai tia \(Ox;Oy\) và tia \(Ot'\) nằm giữa hai tia \(Ox;Oz\) nên tia \(Ox\) nằm giữa hai tia \(Ot;Ot'.\)
Do đó \(\widehat {tOx} + \widehat {t'Ox} = \widehat {tOt'}\) (5)
Từ (4) (5) suy ra \(\widehat {tOx} + \widehat {t'Ox} = \widehat {tOt'} = 90^\circ \).
Cho \(\widehat {AOB},\;\widehat {AOC}\) kề với nhau. Biết \(\widehat {AOB} = \widehat {AOC} = {65^0}\),
Chọn câu đúng.
Tia \(OB\) là tia phân giác của \(\widehat {AOC}\).
Tia \(OC\) là tia phân giác của \(\widehat {BOA}\).
Tia \(OA\) là tia phân giác của \(\widehat {BOC}\).
Không có tia nào là tia phân giác của góc.
Đáp án: C
Sử dụng định nghĩa tia phân giác của một góc
Nếu \(\widehat {xOt} = \widehat {yOt}\) và tia \(Ot\) nằm giữa hai tia \(Ox;Oy\) thì tia $Ot$ là tia phân giác của \(\widehat {xOy}\).
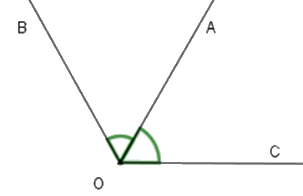
Vì \(\widehat {AOB},\;\widehat {AOC}\) kề với nhau nên tia \(OA\) nằm giữa hai tia \(OB;OC\) mà \(\widehat {AOB} = \widehat {AOC} = {65^0}\) nên tia Tia \(OA\) là tia phân giác của \(\widehat {BOC}\).
Số đo góc \(BOC\) là
\({140^0}\)
\({120^0}\)
\({35^0}\)
\({130^0}\)
Đáp án: D
Sử dụng: Nếu tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)
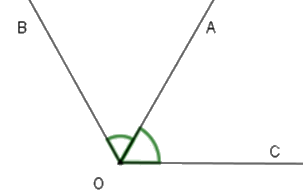
Vì tia \(OA\) là tia phân giác của \(\widehat {BOC}\) (theo câu trước) nên
\(\widehat {AOB} = \widehat {AOC} = \dfrac{{\widehat {BOC}}}{2}\) hay \(\widehat {BOC} = 2.\widehat {AOC} = 2.65^\circ = 130^\circ \).
Cho hai góc kề bù \(\widehat {xOy}\) và \(\widehat {yOz}\) sao cho \(\widehat {xOy} = {120^0}\). Gọi Ot là tia phân giác của \(\widehat {xOy}\), vẽ tia Om trong góc \(\widehat {yOz}\) sao cho \(\widehat {tOm} = {90^0}\).
Tính \(\widehat {yOm}\).
\({30^0}\)
\({40^0}\)
\({35^0}\)
\({60^0}\)
Đáp án: A
+ Sử dụng tính chất tia phân giác để tính \(\widehat {tOy}\)
+ Sử dụng tính chất cộng góc để tính \(\widehat {yOz}\).
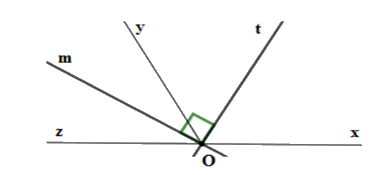
Vì $Ot$ là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {tOy} = \dfrac{{\widehat {xOy}}}{2} = \dfrac{{120^\circ }}{2} = 60^\circ \).
Lại có tia \(Ot\) nằm trong góc \(xOy\) và tia \(Om\) nằm trong góc \(yOz\) mà hai góc \(\widehat {xOy};\,\widehat {yOz}\) là hai góc kề bù nên tia \(Oy\) nằm giữa hai tia \(Om;Ot\). Do đó \(\widehat {tOy} + \widehat {yOm} = \widehat {tOm}\) hay \(\widehat {yOm} = 90^\circ - \widehat {tOy} = 90^\circ - 60^\circ = 30^\circ \).
Vậy \(\widehat {yOm} = 30^\circ \).
Tia \(Om\) là tia phân giác của góc nào?
Tia \(Om\) là tia phân giác của \(\widehat {xOz}\)
Tia \(Om\) là tia phân giác của \(\widehat {mOz}\)
Tia \(Om\) là tia phân giác của \(\widehat {tOz}\)
Tia \(Om\) là tia phân giác của \(\widehat {yOz}\)
Đáp án: D
Sử dụng tổng hai góc kề bù bằng \(180^\circ \) để tính \(\widehat {yOz}\)
Sử dụng công thức cộng góc để tính \(\widehat {mOz}\)
Sử dụng định nghĩa tia phân giác để kết luận.
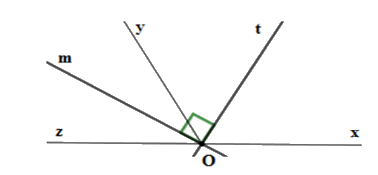
+ Vì \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù nên \(\widehat {xOy} + \widehat {yOz} = 180^\circ \) mà \(\widehat {xOy} = 120^\circ \) nên \(\widehat {yOz} = 180^\circ - 120^\circ = 60^\circ \)
+ Vì tia \(Om\) nằm trong góc \(\widehat {yOz}\) nên tia \(Om\) nằm giữa hai tia \(Oy;Oz\) (1)
Do đó \(\widehat {yOm} + \widehat {mOz} = \widehat {yOz}\) suy ra \(\widehat {mOz} = \widehat {yOz} - \widehat {yOm} = 60^\circ - 30^\circ = 30^\circ \)
Hay \(\widehat {mOz} = \widehat {yOm} = 30^\circ \) (2)
Từ (1) và (2) suy ra tia \(Om\) là tia phân giác của \(\widehat {yOz}\)
Cho góc \(xOy\) bằng \(110^\circ \) có tia \(Oz\) là tia phân giác. Vẽ các tia \(Om;On\) nằm trong góc \(xOy\) sao cho \(\widehat {xOm} = \widehat {yOn} = 30^\circ \).
Tính góc \(zOn\).
\({40^0}\)
\({30^0}\)
\({25^0}\)
\({60^0}\)
Đáp án: C
+ Sử dụng tính chất tia phân giác để tính \(\widehat {yOz}\)
+ Sử dụng dấu hiệu tia nằm giữa hai tia và tính chất cộng góc để tính \(\widehat {zOn}\)
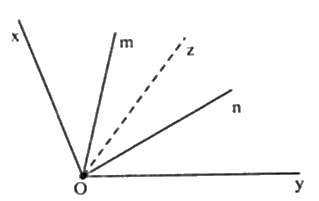
Vì tia \(Oz\) là tia phân giác của góc \(xOy\) nên \(\widehat {xOz} = \widehat {yOz} = \dfrac{1}{2}\widehat {yOx} = \dfrac{1}{2}.110^\circ = 55^\circ \)
Trên nửa mặt phẳng bờ $Oy$ có \(\widehat {yOn} < \widehat {yOz}\,\left( {30^\circ < 55^\circ } \right)\) nên tia \(On\) nằm giữa hai tia \(Oy;Oz\).
Do đó \(\widehat {yOn} + \widehat {nOz} = \widehat {zOy}\) \( \Rightarrow \widehat {zOn} = \widehat {zOy} - \widehat {yOn} = 55^\circ - 30^\circ = 25^\circ \).
Chọn câu đúng.
Tia \(Oz\) là tia phân giác của \(\widehat {xOn}\).
Tia \(Oz\) là tia phân giác của \(\widehat {mOn}\).
Tia \(Oz\) là tia phân giác của \(\widehat {mOy}\).
Tia \(Oz\) là tia phân giác của \(\widehat {xOz}\).
Đáp án: B
Tính góc \(mOz\) từ đó sử dụng định nghĩa để suy ra tia phân giác của một góc.
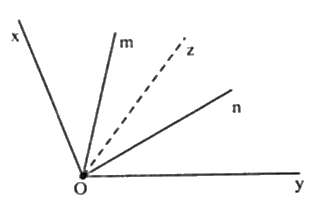
Trên nửa mặt phẳng bờ $Oy$, vì \(\widehat {xOz} = 55^\circ \) (theo câu trước) nên \(\widehat {xOm} < \widehat {xOz}\,\left( {30^\circ < 55^\circ } \right)\) nên tia \(Om\) nằm giữa hai tia \(Ox;Oz\)
Do đó \(\widehat {xOm} + \widehat {mOz} = \widehat {xOz} \Rightarrow \widehat {mOz} = 55^\circ - 30^\circ = 25^\circ \)
Suy ra \(\widehat {mOz} = \widehat {nOz} = 25^\circ \) (1)
Vì \(On\) nằm giữa hai tia \(Oy;Oz\) (theo câu trước) và tia \(Om\)nằm giữa hai tia \(Ox;Oz\) (cmt) nên tia \(Oz\)nằm giữa hai tia \(Om;On\) (2)
Từ (1) và (2) suy ra tia \(Oz\) là tia phân giác của \(\widehat {mOn}\).
Hai đường thẳng \(MN\) và \(PQ\) cắt nhau tại \(O\), tạo thành \(\widehat {MOP} = 50^\circ \) . Cho tia OK là tia phân giác của \(\widehat {PON}\). Chọn khẳng định sai.
\(\widehat {MOQ} = \widehat {PON} = {130^o}\)
\(\widehat {POK} = \widehat {NOK} = 50^\circ \)
\(\widehat {MOQ} + \widehat {QON} = {180^o}\)
\(\widehat {QON} = 50^\circ \)
Đáp án : B
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
+ Sử dụng tính chất tia phân giác của một góc
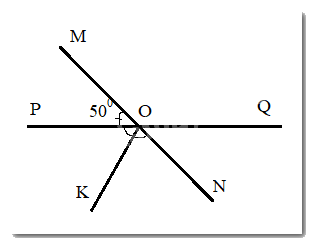
Ta có : \(\widehat {QON} = \widehat {MOP} = 50^\circ \) ( 2 góc đối đỉnh)
\(\widehat {MOQ} + \widehat {QON} = {180^o}\) ( 2 góc kề bù)
\(\widehat {MOP} + \widehat {PON} = 180^\circ \) ( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow 50^\circ + \widehat {PON} = 180^\circ \\ \Rightarrow \widehat {PON} = 180^\circ - 50^\circ = 130^\circ \end{array}\)
Vì OK là tia phân giác của \(\widehat {PON}\)
\( \Rightarrow \widehat {POK} = \widehat {NOK} = \frac{1}{2}.\widehat {PON} = \frac{1}{2}.130^\circ = 65^\circ \)
Vậy khẳng định A, C, D đúng, B sai
Hai đường thẳng \(xy\) và \(x'y'\) cắt nhau tại \(O.\) Biết \(\widehat {xOx'} = {70^o}\). \(Ot\) là tia phân giác của góc xOx’. \(Ot'\) là tia đối của tia \(Ot.\) Tính số đo góc \(yOt'.\)
\(\widehat {yOt'} = {35^o}\)
\(\widehat {yOt'} = {70^o}\)
\(\widehat {yOt'} = {145^o}\)
\(\widehat {yOt'} = {110^o}\)
Đáp án : A
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
+ Sử dụng tính chất tia phân giác của một góc
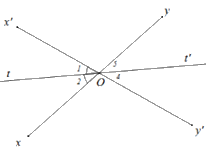
Vì \(Ot\) là tia phân giác của góc \(xOx'\) nên \(\widehat {xOt} = \widehat {tOx'} = \frac{1}{2}\widehat {xOx'} = \frac{1}{2}{.70^o} = {35^o}\)
Vì \(Oy\) là tia đối của \(Ox,Ot'\) là tia đối của \(Ot\)
Suy ra \(\widehat {yOt'} = \widehat {xOt} = {35^o}\) (tính chất hai góc đối đỉnh).
Cho \(\widehat {xOy},\widehat {yOz}\) là 2 góc kề bù. Góc xOy có số đo là 60o . Kẻ Om và On lần lượt là tia phân giác của 2 góc đó. Tính số đo góc mOn
30o
60o
120o
90o
Đáp án : D
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
+ Sử dụng tính chất tia phân giác của một góc
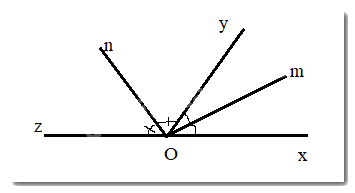
Ta có: \(\widehat {xOy} + \widehat {yOz} = 180^\circ \) ( 2 góc kề bù)
\(\widehat {xOm} = \widehat {mOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.60^\circ = 30^\circ \)
Vì Om là tia phân giác của góc xOy nên \(\widehat {xOm} = \widehat {mOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.60^\circ = 30^\circ \)
Vì On là tia phân giác của góc yOz nên \(\widehat {yOn} = \widehat {nOz} = \frac{1}{2}.\widehat {yOz} = \frac{1}{2}.120^\circ = 60^\circ \)
Vì Oy nằm giữa 2 tia Om và On nên \(\widehat {mOn} = \widehat {mOy} + \widehat {yOn} = 30^\circ + 60^\circ = 90^\circ \)
Hai đường thẳng \(AB\) và \(CD\) cắt nhau tại \(O\). Biết \(\widehat {AOD} - \widehat {AOC} = 60^\circ \) . Gọi \(OM\) là phân giác \(\widehat {AOC}\) và \(ON\) là tia đối của tia \(OM\). Tính \(\widehat {BON}\) và \(\widehat {DON}.\)
\(\widehat {BON} = \widehat {DON} = 25^\circ \)
\(\widehat {BON} = \widehat {DON} = 30^\circ \)
\(\widehat {BON} = \widehat {DON} = 60^\circ \)
\(\widehat {BON} = \widehat {DON} = 45^\circ \)
Đáp án : B
+ Tính số đo góc AOC nhờ bài toán biết tổng và hiệu.
+ Sử dụng tính chất tia phân giác tính các góc \(\widehat {AOM};\widehat {COM}\)
+ Sử dụng tính chất hai góc đối đỉnh để suy ra hai góc \(\widehat {BON}\) và \(\widehat {DON}.\)
Ta có: \(\widehat {mOn} = \widehat {mOy} + \widehat {yOn} = 30^\circ + 60^\circ = 90^\circ \) ( 2 góc kề bù)
Mà \(\widehat {AOD} - \widehat {AOC} = 60^\circ \)
\( \Rightarrow \widehat {AOC} = \left( {180^\circ - 60^\circ } \right):2 = 60^\circ \)
Vì \(AB\) và \(CD\) cắt nhau tại \(O\) nên \(OA\) và \(OB\) là hai tia đối nhau, \(OC\) và \(OD\) là hai tia đối nhau.
Vì \(OM\) là tia phân giác \(\widehat {COA}\) nên \(\widehat {AOM} = \widehat {COM} = \frac{{\widehat {COA}}}{2} = \frac{{60}}{2} = 30^\circ \)
Mà \(ON\) và \(OM\) là hai tia đối nhau nên \(\widehat {AOM}\) và \(\widehat {BON}\) là hai góc đối đỉnh; \(\widehat {COM}\) và \(\widehat {DON}\) là hai góc đối đỉnh
Suy ra \(\widehat {AOM} = \widehat {BON} = 30^\circ ;\widehat {COM} = \widehat {DON} = 30^\circ \) hay \(\widehat {BON} = \widehat {DON} = 30^\circ .\)
Chọn phát biểu sai trong các phát biểu sau:
Nếu tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì tia \(Ot\) nằm giữa hai tia \(Ox;Oy.\)
Nếu tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)
Nếu \(\widehat {xOt} = \widehat {yOt}\) thì tia \(Ot\) là tia phân giác của \(\widehat {xOy}\).
Nếu \(\widehat {xOt} = \widehat {yOt}\) và tia \(Ot\) nằm giữa hai tia \(Ox;Oy\) thì tia \(Ot\) là tia phân giác của \(\widehat {xOy}\).
Cho $Ot$ là tia phân giác của \(\widehat {xOy}\). Biết \(\widehat {xOy} = {100^0}\), số đo của \(\widehat {xOt}\) là:
\({40^0}\)
\({60^0}\)
\({50^0}\)
\({200^0}\)
Cho \(\widehat {xOy}\) là góc vuông có tia On là phân giác, số đo của \(\widehat {xOn}\) là:
\({40^0}\)
\({90^0}\)
\({45^0}\)
\({85^0}\)
Cho tia \(On\) là tia phân giác của \(\widehat {mOt}\). Biết \(\widehat {mOn} = {70^0}\), số đo của \(\widehat {mOt}\) là:
\({140^0}\)
\({120^0}\)
\({35^0}\)
\({60^0}\)
Cho \(\widehat {AOB} = 90^\circ \) và tia \(OB\) là tia phân giác của góc \(AOC.\) Khi đó góc \(AOC\) là
Góc vuông
Góc nhọn
Góc tù
Góc bẹt
Cho \(\widehat {AOC} = {60^0}\). Vẽ tia \(OB\) sao cho \(OA\) là tia phân giác của \(\widehat {BOC}\). Tính số đo của \(\widehat {AOB}\) và \(\widehat {BOC}\).
\(\widehat {AOB} = 70^\circ ;\,\widehat {BOC} = 140^\circ \)
\(\widehat {AOB} = 90^\circ ;\,\widehat {BOC} = 120^\circ \)
\(\widehat {AOB} = 120^\circ ;\,\widehat {BOC} = 60^\circ \)
\(\widehat {AOB} = 60^\circ ;\,\widehat {BOC} = 120^\circ \)
Cho \(\widehat {AOB} = {110^0}\) và \(\widehat {AOC} = {55^0}\) sao cho \(\widehat {AOB}\) và \(\widehat {AOC}\) không kề nhau. Chọn câu sai.
Tia \(OC\) nằm giữa hai tia \(OA\) và \(OB.\)
Tia \(OC\) là tia phân giác góc \(AOB.\)
\(\widehat {BOC} = 65^\circ \)
\(\widehat {BOC} = 55^\circ \)
Cho \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù. Biết \(\widehat {xOy} = 120^\circ \) và tia \(Ot\) là tia phân giác của \(\widehat {yOz}.\) Tính số đo góc \(xOt.\)
\({140^0}\)
\({150^0}\)
\({90^0}\)
\({120^0}\)
Cho góc \(AOB\) và tia phân giác \(OC\) của góc đó. Vẽ tia phân giác \(OM\) của góc \(BOC.\) Biết \(\widehat {BOM} = 35^\circ .\) Tính số đo góc \(AOB.\)
\({150^0}\)
\({120^0}\)
\({140^0}\)
\({160^0}\)
Cho góc bẹt \(xOy\). Trên cùng một nửa mặt phẳng bờ \(xy\) vẽ các tia \(Om;On\) sao cho \(\widehat {xOm} = a^\circ \,\left( {a < 180} \right)\) và \(\widehat {yOn} = 70^\circ .\) Với giá trị nào của \(a\) thì tia \(On\) là tia phân giác của \(\widehat {yOm}\).
\({45^0}\)
\({30^0}\)
\({50^0}\)
\({40^0}\)
Cho hai góc kề bù \(\widehat {xOy};\,\widehat {xOz}\). Vẽ tia \(Ot\) là phân giác \(\widehat {xOy}\) và tia \(Ot'\) là phân giác \(\widehat {xOz}\). Tính \(\widehat {tOt'}\).
\({70^0}\)
\({80^0}\)
\({60^0}\)
\({90^0}\)
Cho \(\widehat {AOB},\;\widehat {AOC}\) kề với nhau. Biết \(\widehat {AOB} = \widehat {AOC} = {65^0}\),
Chọn câu đúng.
Tia \(OB\) là tia phân giác của \(\widehat {AOC}\).
Tia \(OC\) là tia phân giác của \(\widehat {BOA}\).
Tia \(OA\) là tia phân giác của \(\widehat {BOC}\).
Không có tia nào là tia phân giác của góc.
Số đo góc \(BOC\) là
\({140^0}\)
\({120^0}\)
\({35^0}\)
\({130^0}\)
Cho hai góc kề bù \(\widehat {xOy}\) và \(\widehat {yOz}\) sao cho \(\widehat {xOy} = {120^0}\). Gọi Ot là tia phân giác của \(\widehat {xOy}\), vẽ tia Om trong góc \(\widehat {yOz}\) sao cho \(\widehat {tOm} = {90^0}\).
Tính \(\widehat {yOm}\).
\({30^0}\)
\({40^0}\)
\({35^0}\)
\({60^0}\)
Tia \(Om\) là tia phân giác của góc nào?
Tia \(Om\) là tia phân giác của \(\widehat {xOz}\)
Tia \(Om\) là tia phân giác của \(\widehat {mOz}\)
Tia \(Om\) là tia phân giác của \(\widehat {tOz}\)
Tia \(Om\) là tia phân giác của \(\widehat {yOz}\)
Cho góc \(xOy\) bằng \(110^\circ \) có tia \(Oz\) là tia phân giác. Vẽ các tia \(Om;On\) nằm trong góc \(xOy\) sao cho \(\widehat {xOm} = \widehat {yOn} = 30^\circ \).
Tính góc \(zOn\).
\({40^0}\)
\({30^0}\)
\({25^0}\)
\({60^0}\)
Chọn câu đúng.
Tia \(Oz\) là tia phân giác của \(\widehat {xOn}\).
Tia \(Oz\) là tia phân giác của \(\widehat {mOn}\).
Tia \(Oz\) là tia phân giác của \(\widehat {mOy}\).
Tia \(Oz\) là tia phân giác của \(\widehat {xOz}\).
Hai đường thẳng \(MN\) và \(PQ\) cắt nhau tại \(O\), tạo thành \(\widehat {MOP} = 50^\circ \) . Cho tia OK là tia phân giác của \(\widehat {PON}\). Chọn khẳng định sai.
\(\widehat {MOQ} = \widehat {PON} = {130^o}\)
\(\widehat {POK} = \widehat {NOK} = 50^\circ \)
\(\widehat {MOQ} + \widehat {QON} = {180^o}\)
\(\widehat {QON} = 50^\circ \)
Hai đường thẳng \(xy\) và \(x'y'\) cắt nhau tại \(O.\) Biết \(\widehat {xOx'} = {70^o}\). \(Ot\) là tia phân giác của góc xOx’. \(Ot'\) là tia đối của tia \(Ot.\) Tính số đo góc \(yOt'.\)
\(\widehat {yOt'} = {35^o}\)
\(\widehat {yOt'} = {70^o}\)
\(\widehat {yOt'} = {145^o}\)
\(\widehat {yOt'} = {110^o}\)
Cho \(\widehat {xOy},\widehat {yOz}\) là 2 góc kề bù. Góc xOy có số đo là 60o . Kẻ Om và On lần lượt là tia phân giác của 2 góc đó. Tính số đo góc mOn
30o
60o
120o
90o
Hai đường thẳng \(AB\) và \(CD\) cắt nhau tại \(O\). Biết \(\widehat {AOD} - \widehat {AOC} = 60^\circ \) . Gọi \(OM\) là phân giác \(\widehat {AOC}\) và \(ON\) là tia đối của tia \(OM\). Tính \(\widehat {BON}\) và \(\widehat {DON}.\)
\(\widehat {BON} = \widehat {DON} = 25^\circ \)
\(\widehat {BON} = \widehat {DON} = 30^\circ \)
\(\widehat {BON} = \widehat {DON} = 60^\circ \)
\(\widehat {BON} = \widehat {DON} = 45^\circ \)
Chọn phát biểu sai trong các phát biểu sau:
Nếu tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì tia \(Ot\) nằm giữa hai tia \(Ox;Oy.\)
Nếu tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)
Nếu \(\widehat {xOt} = \widehat {yOt}\) thì tia \(Ot\) là tia phân giác của \(\widehat {xOy}\).
Nếu \(\widehat {xOt} = \widehat {yOt}\) và tia \(Ot\) nằm giữa hai tia \(Ox;Oy\) thì tia \(Ot\) là tia phân giác của \(\widehat {xOy}\).
Đáp án : C
Nếu \(\widehat {xOt} = \widehat {yOt}\) và tia \(Ot\) nằm giữa hai tia \(Ox;Oy\) thì tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) nên C sai, D đúng.
Cho $Ot$ là tia phân giác của \(\widehat {xOy}\). Biết \(\widehat {xOy} = {100^0}\), số đo của \(\widehat {xOt}\) là:
\({40^0}\)
\({60^0}\)
\({50^0}\)
\({200^0}\)
Đáp án : C
Nếu tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)
Vì tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2} = \dfrac{{100^\circ }}{2} = 50^\circ \)
Cho \(\widehat {xOy}\) là góc vuông có tia On là phân giác, số đo của \(\widehat {xOn}\) là:
\({40^0}\)
\({90^0}\)
\({45^0}\)
\({85^0}\)
Đáp án : C
+ Góc vuông là góc có số đo bằng \(90^\circ \)
+ Sử dụng: Nếu tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)
Vì \(On\) là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOn} = \widehat {nOy} = \dfrac{{\widehat {xOy}}}{2} = \dfrac{{90^\circ }}{2} = 45^\circ \)
Cho tia \(On\) là tia phân giác của \(\widehat {mOt}\). Biết \(\widehat {mOn} = {70^0}\), số đo của \(\widehat {mOt}\) là:
\({140^0}\)
\({120^0}\)
\({35^0}\)
\({60^0}\)
Đáp án : A
Sử dụng: Nếu tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)
Vì tia \(On\) là tia phân giác của \(\widehat {mOt}\) nên \(\widehat {mOn} = \widehat {nOt} = \dfrac{{\widehat {mOt}}}{2}\)
\( \Rightarrow \widehat {mOt} = 2.\widehat {mOn} = 2.70^\circ = 140^\circ \).
Cho \(\widehat {AOB} = 90^\circ \) và tia \(OB\) là tia phân giác của góc \(AOC.\) Khi đó góc \(AOC\) là
Góc vuông
Góc nhọn
Góc tù
Góc bẹt
Đáp án : D
Sử dụng: Nếu tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)

Vì tia \(OB\) là tia phân giác của góc \(AOC\) nên \(\widehat {AOB} = \widehat {BOC} = \dfrac{{\widehat {AOC}}}{2}\)
Do đó \(\widehat {AOC} = 2.\widehat {AOB} = 2.90^\circ = 180^\circ \)
Nên góc \(AOC\) là góc bẹt.
Cho \(\widehat {AOC} = {60^0}\). Vẽ tia \(OB\) sao cho \(OA\) là tia phân giác của \(\widehat {BOC}\). Tính số đo của \(\widehat {AOB}\) và \(\widehat {BOC}\).
\(\widehat {AOB} = 70^\circ ;\,\widehat {BOC} = 140^\circ \)
\(\widehat {AOB} = 90^\circ ;\,\widehat {BOC} = 120^\circ \)
\(\widehat {AOB} = 120^\circ ;\,\widehat {BOC} = 60^\circ \)
\(\widehat {AOB} = 60^\circ ;\,\widehat {BOC} = 120^\circ \)
Đáp án : D
Sử dụng: Nếu tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)

Vì tia \(OA\) là tia phân giác của \(\widehat {BOC}\) nên ta có
\(\widehat {AOB} = \widehat {AOC} = \dfrac{{\widehat {BOC}}}{2}\) nên \(\widehat {AOB} = 60^\circ ;\,\widehat {BOC} = 2.\widehat {AOC} = 2.60^\circ = 120^\circ \)
Vậy \(\widehat {AOB} = 60^\circ ;\,\widehat {BOC} = 120^\circ \).
Cho \(\widehat {AOB} = {110^0}\) và \(\widehat {AOC} = {55^0}\) sao cho \(\widehat {AOB}\) và \(\widehat {AOC}\) không kề nhau. Chọn câu sai.
Tia \(OC\) nằm giữa hai tia \(OA\) và \(OB.\)
Tia \(OC\) là tia phân giác góc \(AOB.\)
\(\widehat {BOC} = 65^\circ \)
\(\widehat {BOC} = 55^\circ \)
Đáp án : C
+ Sử dụng dấu hiệu nhận biết tia nằm giữa hai tia
+ Tính góc \(BOC\)
+ Sử dụng định nghĩa tia phân giác

Vì \(\widehat {AOB}\) và \(\widehat {AOC}\) không kề nhau nên hai tia \(OC;OB\) thuộc cùng nửa mặt phẳng bờ là đường thẳng chứa tia \(OA\). Lại có \(\widehat {AOC} < \widehat {AOB}\,\left( {55^\circ < 110^\circ } \right)\) nên tia \(OC\) nằm giữa hai tia \(OA\) và \(OB.\) (1)
Từ đó \(\widehat {AOC} + \widehat {COB} = \widehat {AOB}\,\) hay \(\widehat {COB} = \widehat {AOB} - \widehat {AOC} = 110^\circ - 55^\circ = 55^\circ \)
Suy ra \(\widehat {AOC} = \widehat {BOC} = 55^\circ \) (2)
Từ (1) và (2) suy ra tia \(OC\) là tia phân giác góc \(AOB.\)
Vậy A, B, D đúng và C sai.
Cho \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù. Biết \(\widehat {xOy} = 120^\circ \) và tia \(Ot\) là tia phân giác của \(\widehat {yOz}.\) Tính số đo góc \(xOt.\)
\({140^0}\)
\({150^0}\)
\({90^0}\)
\({120^0}\)
Đáp án : B
+ Sử dụng: Hai góc kề bù có tổng số đo bằng \(180^\circ \) và tính chất tia phân giác của một góc để tính toán.

Vì \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù nên \(\widehat {xOy} + \widehat {yOz} = 180^\circ \) mà \(\widehat {xOy} = 120^\circ \) nên \(\widehat {yOz} = 180^\circ - 120^\circ = 60^\circ \).
Lại có tia \(Ot\) là tia phân giác của \(\widehat {yOz}\) nên \(\widehat {zOt} = \dfrac{1}{2}\widehat {yOz} = \dfrac{1}{2}.60^\circ = 30^\circ \)
Lại có \(\widehat {zOt};\,\widehat {tOx}\) là hai góc kề bù nên \(\widehat {zOt} + \widehat {tOx} = 180^\circ \Rightarrow \widehat {tOx} = 180^\circ - \widehat {zOt}\)\( = 180^\circ - 30^\circ = 150^\circ .\)
Vậy \(\widehat {tOx} = 150^\circ .\)
Cho góc \(AOB\) và tia phân giác \(OC\) của góc đó. Vẽ tia phân giác \(OM\) của góc \(BOC.\) Biết \(\widehat {BOM} = 35^\circ .\) Tính số đo góc \(AOB.\)
\({150^0}\)
\({120^0}\)
\({140^0}\)
\({160^0}\)
Đáp án : C
Sử dụng: Nếu tia \(Ot\) là tiam phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)

Vì tia \(OM\) là tia phân của góc \(BOC\)
nên \(\widehat {BOC} = 2.\widehat {BOM} = 2.35^\circ = 70^\circ \)
Lại có tia \(OC\) là tia phân giác của \(\widehat {AOB}\) nên \(\widehat {AOB} = 2.\widehat {BOC} = 2.70^\circ = 140^\circ \). Vậy \(\widehat {AOB} = 140^\circ \).
Cho góc bẹt \(xOy\). Trên cùng một nửa mặt phẳng bờ \(xy\) vẽ các tia \(Om;On\) sao cho \(\widehat {xOm} = a^\circ \,\left( {a < 180} \right)\) và \(\widehat {yOn} = 70^\circ .\) Với giá trị nào của \(a\) thì tia \(On\) là tia phân giác của \(\widehat {yOm}\).
\({45^0}\)
\({30^0}\)
\({50^0}\)
\({40^0}\)
Đáp án : D
Sử dụng tính chất tia phân giác và tính chất hai góc kề bù.

Giả sử tia \(On\) là tia phân giác của góc \(yOm\) thì \(\widehat {mOy} = 2.\widehat {yOn} = 2.70^\circ = 140^\circ \).
Mà hai góc \(\widehat {xOm};\widehat {yOm}\) là hai góc kề bù nên \(\widehat {xOm} + \widehat {yOm} = 180^\circ \)\( \Rightarrow \widehat {xOm} = 180^\circ - \widehat {yOm}\) \( = 180^\circ - 140^\circ = 40^\circ \).
Vậy \(a = 40 ^\circ\).
Cho hai góc kề bù \(\widehat {xOy};\,\widehat {xOz}\). Vẽ tia \(Ot\) là phân giác \(\widehat {xOy}\) và tia \(Ot'\) là phân giác \(\widehat {xOz}\). Tính \(\widehat {tOt'}\).
\({70^0}\)
\({80^0}\)
\({60^0}\)
\({90^0}\)
Đáp án : D
+ Sử dụng tính chất hai góc kề bù và tính chất tia phân giác của một góc để tính toán

Vì tia \(Ot\) là phân giác \(\widehat {xOy}\) nên \(\widehat {yOt} = \widehat {xOt} = \dfrac{1}{2}\widehat {xOy}\) suy ra \(\widehat {xOy} = 2.\widehat {tOx}\) (1)
Và tia \(Ot'\) là phân giác \(\widehat {yOz}\) nên \(\widehat {zOt'} = \widehat {xOt'} = \dfrac{1}{2}\widehat {xOz}\) suy ra \(\widehat {xOz} = 2.\widehat {t'Ox}\) (2)
Mà \(\widehat {xOy};\,\widehat {xOz}\) là hai góc kề bù nên \(\widehat {xOy} + \widehat {xOz} = 180^\circ \) (3)
Từ (1) (2) (3) suy ra \(2.\widehat {tOx} + 2.\widehat {t'Ox} = 180^\circ \) suy ra \(2.\left( {\widehat {tOx} + \widehat {t'Ox}} \right) = 180^\circ \Rightarrow \widehat {tOx} + \widehat {t'Ox} = 90^\circ \) (4)
Lại có tia \(Ot\) nằm giữa hai tia \(Ox;Oy\) và tia \(Ot'\) nằm giữa hai tia \(Ox;Oz\) nên tia \(Ox\) nằm giữa hai tia \(Ot;Ot'.\)
Do đó \(\widehat {tOx} + \widehat {t'Ox} = \widehat {tOt'}\) (5)
Từ (4) (5) suy ra \(\widehat {tOx} + \widehat {t'Ox} = \widehat {tOt'} = 90^\circ \).
Cho \(\widehat {AOB},\;\widehat {AOC}\) kề với nhau. Biết \(\widehat {AOB} = \widehat {AOC} = {65^0}\),
Chọn câu đúng.
Tia \(OB\) là tia phân giác của \(\widehat {AOC}\).
Tia \(OC\) là tia phân giác của \(\widehat {BOA}\).
Tia \(OA\) là tia phân giác của \(\widehat {BOC}\).
Không có tia nào là tia phân giác của góc.
Đáp án: C
Sử dụng định nghĩa tia phân giác của một góc
Nếu \(\widehat {xOt} = \widehat {yOt}\) và tia \(Ot\) nằm giữa hai tia \(Ox;Oy\) thì tia $Ot$ là tia phân giác của \(\widehat {xOy}\).

Vì \(\widehat {AOB},\;\widehat {AOC}\) kề với nhau nên tia \(OA\) nằm giữa hai tia \(OB;OC\) mà \(\widehat {AOB} = \widehat {AOC} = {65^0}\) nên tia Tia \(OA\) là tia phân giác của \(\widehat {BOC}\).
Số đo góc \(BOC\) là
\({140^0}\)
\({120^0}\)
\({35^0}\)
\({130^0}\)
Đáp án: D
Sử dụng: Nếu tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)

Vì tia \(OA\) là tia phân giác của \(\widehat {BOC}\) (theo câu trước) nên
\(\widehat {AOB} = \widehat {AOC} = \dfrac{{\widehat {BOC}}}{2}\) hay \(\widehat {BOC} = 2.\widehat {AOC} = 2.65^\circ = 130^\circ \).
Cho hai góc kề bù \(\widehat {xOy}\) và \(\widehat {yOz}\) sao cho \(\widehat {xOy} = {120^0}\). Gọi Ot là tia phân giác của \(\widehat {xOy}\), vẽ tia Om trong góc \(\widehat {yOz}\) sao cho \(\widehat {tOm} = {90^0}\).
Tính \(\widehat {yOm}\).
\({30^0}\)
\({40^0}\)
\({35^0}\)
\({60^0}\)
Đáp án: A
+ Sử dụng tính chất tia phân giác để tính \(\widehat {tOy}\)
+ Sử dụng tính chất cộng góc để tính \(\widehat {yOz}\).

Vì $Ot$ là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {tOy} = \dfrac{{\widehat {xOy}}}{2} = \dfrac{{120^\circ }}{2} = 60^\circ \).
Lại có tia \(Ot\) nằm trong góc \(xOy\) và tia \(Om\) nằm trong góc \(yOz\) mà hai góc \(\widehat {xOy};\,\widehat {yOz}\) là hai góc kề bù nên tia \(Oy\) nằm giữa hai tia \(Om;Ot\). Do đó \(\widehat {tOy} + \widehat {yOm} = \widehat {tOm}\) hay \(\widehat {yOm} = 90^\circ - \widehat {tOy} = 90^\circ - 60^\circ = 30^\circ \).
Vậy \(\widehat {yOm} = 30^\circ \).
Tia \(Om\) là tia phân giác của góc nào?
Tia \(Om\) là tia phân giác của \(\widehat {xOz}\)
Tia \(Om\) là tia phân giác của \(\widehat {mOz}\)
Tia \(Om\) là tia phân giác của \(\widehat {tOz}\)
Tia \(Om\) là tia phân giác của \(\widehat {yOz}\)
Đáp án: D
Sử dụng tổng hai góc kề bù bằng \(180^\circ \) để tính \(\widehat {yOz}\)
Sử dụng công thức cộng góc để tính \(\widehat {mOz}\)
Sử dụng định nghĩa tia phân giác để kết luận.

+ Vì \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù nên \(\widehat {xOy} + \widehat {yOz} = 180^\circ \) mà \(\widehat {xOy} = 120^\circ \) nên \(\widehat {yOz} = 180^\circ - 120^\circ = 60^\circ \)
+ Vì tia \(Om\) nằm trong góc \(\widehat {yOz}\) nên tia \(Om\) nằm giữa hai tia \(Oy;Oz\) (1)
Do đó \(\widehat {yOm} + \widehat {mOz} = \widehat {yOz}\) suy ra \(\widehat {mOz} = \widehat {yOz} - \widehat {yOm} = 60^\circ - 30^\circ = 30^\circ \)
Hay \(\widehat {mOz} = \widehat {yOm} = 30^\circ \) (2)
Từ (1) và (2) suy ra tia \(Om\) là tia phân giác của \(\widehat {yOz}\)
Cho góc \(xOy\) bằng \(110^\circ \) có tia \(Oz\) là tia phân giác. Vẽ các tia \(Om;On\) nằm trong góc \(xOy\) sao cho \(\widehat {xOm} = \widehat {yOn} = 30^\circ \).
Tính góc \(zOn\).
\({40^0}\)
\({30^0}\)
\({25^0}\)
\({60^0}\)
Đáp án: C
+ Sử dụng tính chất tia phân giác để tính \(\widehat {yOz}\)
+ Sử dụng dấu hiệu tia nằm giữa hai tia và tính chất cộng góc để tính \(\widehat {zOn}\)

Vì tia \(Oz\) là tia phân giác của góc \(xOy\) nên \(\widehat {xOz} = \widehat {yOz} = \dfrac{1}{2}\widehat {yOx} = \dfrac{1}{2}.110^\circ = 55^\circ \)
Trên nửa mặt phẳng bờ $Oy$ có \(\widehat {yOn} < \widehat {yOz}\,\left( {30^\circ < 55^\circ } \right)\) nên tia \(On\) nằm giữa hai tia \(Oy;Oz\).
Do đó \(\widehat {yOn} + \widehat {nOz} = \widehat {zOy}\) \( \Rightarrow \widehat {zOn} = \widehat {zOy} - \widehat {yOn} = 55^\circ - 30^\circ = 25^\circ \).
Chọn câu đúng.
Tia \(Oz\) là tia phân giác của \(\widehat {xOn}\).
Tia \(Oz\) là tia phân giác của \(\widehat {mOn}\).
Tia \(Oz\) là tia phân giác của \(\widehat {mOy}\).
Tia \(Oz\) là tia phân giác của \(\widehat {xOz}\).
Đáp án: B
Tính góc \(mOz\) từ đó sử dụng định nghĩa để suy ra tia phân giác của một góc.

Trên nửa mặt phẳng bờ $Oy$, vì \(\widehat {xOz} = 55^\circ \) (theo câu trước) nên \(\widehat {xOm} < \widehat {xOz}\,\left( {30^\circ < 55^\circ } \right)\) nên tia \(Om\) nằm giữa hai tia \(Ox;Oz\)
Do đó \(\widehat {xOm} + \widehat {mOz} = \widehat {xOz} \Rightarrow \widehat {mOz} = 55^\circ - 30^\circ = 25^\circ \)
Suy ra \(\widehat {mOz} = \widehat {nOz} = 25^\circ \) (1)
Vì \(On\) nằm giữa hai tia \(Oy;Oz\) (theo câu trước) và tia \(Om\)nằm giữa hai tia \(Ox;Oz\) (cmt) nên tia \(Oz\)nằm giữa hai tia \(Om;On\) (2)
Từ (1) và (2) suy ra tia \(Oz\) là tia phân giác của \(\widehat {mOn}\).
Hai đường thẳng \(MN\) và \(PQ\) cắt nhau tại \(O\), tạo thành \(\widehat {MOP} = 50^\circ \) . Cho tia OK là tia phân giác của \(\widehat {PON}\). Chọn khẳng định sai.
\(\widehat {MOQ} = \widehat {PON} = {130^o}\)
\(\widehat {POK} = \widehat {NOK} = 50^\circ \)
\(\widehat {MOQ} + \widehat {QON} = {180^o}\)
\(\widehat {QON} = 50^\circ \)
Đáp án : B
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
+ Sử dụng tính chất tia phân giác của một góc

Ta có : \(\widehat {QON} = \widehat {MOP} = 50^\circ \) ( 2 góc đối đỉnh)
\(\widehat {MOQ} + \widehat {QON} = {180^o}\) ( 2 góc kề bù)
\(\widehat {MOP} + \widehat {PON} = 180^\circ \) ( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow 50^\circ + \widehat {PON} = 180^\circ \\ \Rightarrow \widehat {PON} = 180^\circ - 50^\circ = 130^\circ \end{array}\)
Vì OK là tia phân giác của \(\widehat {PON}\)
\( \Rightarrow \widehat {POK} = \widehat {NOK} = \frac{1}{2}.\widehat {PON} = \frac{1}{2}.130^\circ = 65^\circ \)
Vậy khẳng định A, C, D đúng, B sai
Hai đường thẳng \(xy\) và \(x'y'\) cắt nhau tại \(O.\) Biết \(\widehat {xOx'} = {70^o}\). \(Ot\) là tia phân giác của góc xOx’. \(Ot'\) là tia đối của tia \(Ot.\) Tính số đo góc \(yOt'.\)
\(\widehat {yOt'} = {35^o}\)
\(\widehat {yOt'} = {70^o}\)
\(\widehat {yOt'} = {145^o}\)
\(\widehat {yOt'} = {110^o}\)
Đáp án : A
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
+ Sử dụng tính chất tia phân giác của một góc

Vì \(Ot\) là tia phân giác của góc \(xOx'\) nên \(\widehat {xOt} = \widehat {tOx'} = \frac{1}{2}\widehat {xOx'} = \frac{1}{2}{.70^o} = {35^o}\)
Vì \(Oy\) là tia đối của \(Ox,Ot'\) là tia đối của \(Ot\)
Suy ra \(\widehat {yOt'} = \widehat {xOt} = {35^o}\) (tính chất hai góc đối đỉnh).
Cho \(\widehat {xOy},\widehat {yOz}\) là 2 góc kề bù. Góc xOy có số đo là 60o . Kẻ Om và On lần lượt là tia phân giác của 2 góc đó. Tính số đo góc mOn
30o
60o
120o
90o
Đáp án : D
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
+ Sử dụng tính chất tia phân giác của một góc

Ta có: \(\widehat {xOy} + \widehat {yOz} = 180^\circ \) ( 2 góc kề bù)
\(\widehat {xOm} = \widehat {mOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.60^\circ = 30^\circ \)
Vì Om là tia phân giác của góc xOy nên \(\widehat {xOm} = \widehat {mOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.60^\circ = 30^\circ \)
Vì On là tia phân giác của góc yOz nên \(\widehat {yOn} = \widehat {nOz} = \frac{1}{2}.\widehat {yOz} = \frac{1}{2}.120^\circ = 60^\circ \)
Vì Oy nằm giữa 2 tia Om và On nên \(\widehat {mOn} = \widehat {mOy} + \widehat {yOn} = 30^\circ + 60^\circ = 90^\circ \)
Hai đường thẳng \(AB\) và \(CD\) cắt nhau tại \(O\). Biết \(\widehat {AOD} - \widehat {AOC} = 60^\circ \) . Gọi \(OM\) là phân giác \(\widehat {AOC}\) và \(ON\) là tia đối của tia \(OM\). Tính \(\widehat {BON}\) và \(\widehat {DON}.\)
\(\widehat {BON} = \widehat {DON} = 25^\circ \)
\(\widehat {BON} = \widehat {DON} = 30^\circ \)
\(\widehat {BON} = \widehat {DON} = 60^\circ \)
\(\widehat {BON} = \widehat {DON} = 45^\circ \)
Đáp án : B
+ Tính số đo góc AOC nhờ bài toán biết tổng và hiệu.
+ Sử dụng tính chất tia phân giác tính các góc \(\widehat {AOM};\widehat {COM}\)
+ Sử dụng tính chất hai góc đối đỉnh để suy ra hai góc \(\widehat {BON}\) và \(\widehat {DON}.\)

Ta có: \(\widehat {mOn} = \widehat {mOy} + \widehat {yOn} = 30^\circ + 60^\circ = 90^\circ \) ( 2 góc kề bù)
Mà \(\widehat {AOD} - \widehat {AOC} = 60^\circ \)
\( \Rightarrow \widehat {AOC} = \left( {180^\circ - 60^\circ } \right):2 = 60^\circ \)
Vì \(AB\) và \(CD\) cắt nhau tại \(O\) nên \(OA\) và \(OB\) là hai tia đối nhau, \(OC\) và \(OD\) là hai tia đối nhau.
Vì \(OM\) là tia phân giác \(\widehat {COA}\) nên \(\widehat {AOM} = \widehat {COM} = \frac{{\widehat {COA}}}{2} = \frac{{60}}{2} = 30^\circ \)
Mà \(ON\) và \(OM\) là hai tia đối nhau nên \(\widehat {AOM}\) và \(\widehat {BON}\) là hai góc đối đỉnh; \(\widehat {COM}\) và \(\widehat {DON}\) là hai góc đối đỉnh
Suy ra \(\widehat {AOM} = \widehat {BON} = 30^\circ ;\widehat {COM} = \widehat {DON} = 30^\circ \) hay \(\widehat {BON} = \widehat {DON} = 30^\circ .\)
Bài 2 trong chương trình Toán 7 Cánh diều tập trung vào khái niệm quan trọng: tia phân giác của một góc. Hiểu rõ về tia phân giác là nền tảng để giải quyết nhiều bài toán hình học trong các lớp học tiếp theo. Bài viết này sẽ cung cấp một tổng quan đầy đủ về lý thuyết, các định nghĩa, tính chất và đặc biệt là các dạng bài tập trắc nghiệm thường gặp.
Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo thành hai góc bằng nhau. Để xác định một tia là tia phân giác, cần chứng minh:
Một trong những tính chất quan trọng nhất của tia phân giác là:
Tính chất 1: Nếu một điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
Tính chất 2: Nếu một điểm cách đều hai cạnh của một góc thì nằm trên tia phân giác của góc đó.
Loại bài tập này yêu cầu học sinh quan sát hình vẽ, đo góc và xác định xem tia nào là tia phân giác. Cần lưu ý sử dụng thước đo góc chính xác và áp dụng định nghĩa về tia phân giác.
Nếu biết một góc và tia phân giác của nó, học sinh có thể tính số đo của mỗi góc nhỏ tạo thành bằng cách chia góc lớn cho 2.
Để chứng minh một tia là tia phân giác, cần chứng minh tia đó nằm giữa hai cạnh của góc và tạo thành hai góc bằng nhau. Có thể sử dụng các định lý, tính chất đã học để chứng minh.
Dựa vào tính chất nếu một điểm cách đều hai cạnh của một góc thì nằm trên tia phân giác, học sinh có thể giải quyết các bài toán liên quan đến việc tìm điểm nằm trên tia phân giác.
Ví dụ 1: Cho góc ABC có số đo 80 độ. Tia BD là tia phân giác của góc ABC. Tính số đo góc ABD?
Giải: Vì BD là tia phân giác của góc ABC nên góc ABD = góc DBC = góc ABC / 2 = 80 độ / 2 = 40 độ.
Ví dụ 2: Cho tam giác ABC, tia phân giác AM (M thuộc BC). Biết góc BAM = 30 độ. Tính góc MAC?
Giải: Vì AM là tia phân giác của góc BAC nên góc MAC = góc BAM = 30 độ.
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập trắc nghiệm nâng cao sau:
Tia phân giác của một góc là một khái niệm cơ bản nhưng vô cùng quan trọng trong chương trình Toán 7. Việc nắm vững lý thuyết, tính chất và các dạng bài tập trắc nghiệm liên quan sẽ giúp các em học sinh tự tin hơn trong quá trình học tập và giải quyết các bài toán hình học. Hãy luyện tập thường xuyên và áp dụng kiến thức vào thực tế để đạt kết quả tốt nhất!
| Khái niệm | Định nghĩa |
|---|---|
| Tia phân giác | Tia nằm giữa hai cạnh của góc và tạo thành hai góc bằng nhau. |
| Nguồn: giaitoan.edu.vn | |