Bài viết này cung cấp bộ câu hỏi trắc nghiệm giúp học sinh ôn luyện và kiểm tra kiến thức về tính chất ba đường trung trực của tam giác trong chương trình Toán 7 Cánh diều. Các câu hỏi được thiết kế đa dạng, bao gồm nhiều mức độ khó khác nhau, giúp học sinh rèn luyện kỹ năng giải bài tập.
Giaitoan.edu.vn luôn đồng hành cùng học sinh trên con đường chinh phục môn Toán. Chúc các em học tốt!
Cho tam giác \(ABC\) có \(\widehat A\) là góc tù. Tia phân giác của góc \(B\) và góc \(C\) cắt nhau tại \(O.\) Lấy điểm \(E\) trên cạnh \(AB.\) Từ \(E\) kẻ \(EP \bot BO\,\,\left( {P \in BC} \right).\) Từ \(P\) kẻ \(PF \bot OC\,\left( {F \in AC} \right).\)
Chọn câu đúng.
\(OB\) là đường trung trực của đoạn \(EP\)
\(OC\) là đường trung trực của đoạn \(PF\)
Cả A, B đều đúng
Cả A,B đều sai
So sánh \(BE + CF\) và \(BC.\)
\(BE + CF > BC\)
\(BE + CF < BC\)
\(BE + CF = BC\)
\(BE + CF = \dfrac{1}{2}BC\)
Cho \(\Delta ABC\) nhọn, đường cao $AH.$ Lấy điểm $D$ sao cho $AB$ là trung trực của $HD.$ Lấy điểm $E$ sao cho $AC$ là trung trực của $HE.$ Gọi $M$ là giao điểm của $DE$ với $AB,N$ là giao điểm của $DE$ với $AC.$ Chọn câu đúng.
\(\Delta ADE\) là tam giác cân
$HA$ là tia phân giác của \(\widehat {MHN}\).
A, B đều đúng
A, B đều sai
Cho tam giác $ABC$ vuông tại $A,$ kẻ đường cao $AH.$ Trên cạnh $AC$ lấy điểm $K$ sao cho $AK = AH.$ Kẻ \(KD \bot AC\left( {D \in BC} \right)\). Chọn câu đúng.
\(\Delta AHD = \Delta AKD\)
$AD$ là đường trung trực của đoạn thẳng $HK.$
\(AD\) là tia phân giác của góc \(HAK.\)
Cả A, B, C đều đúng.
Cho tam giác \(ABC\) trong đó \(\widehat A = 100^\circ \). Các đường trung trực của \(AB\) và \(AC\) cắt cạnh \(BC\) theo thứ tự ở \(E\) và \(F\) . Tính \(\widehat {EAF}.\)
\(20^\circ \)
\(30^\circ \)
\(40^\circ \)
\(50^\circ \)
Cho tam giác \(ABC\) có \(AC > AB.\) Trên cạnh \(AC\) lấy điểm \(E\) sao cho \(CE = AB.\) Các đường trung trực của \(BE\) và \(AC\) cắt nhau tại \(O.\)
Chọn câu đúng.
\(\Delta ABO = \Delta COE\)
\(\Delta BOA = \Delta COE\)
\(\Delta AOB = \Delta COE\)
\(\Delta ABO = \Delta CEO\)
Chọn câu đúng
\(AO\) là đường trung tuyến của tam giác \(ABC.\)
\(AO\) là đường trung trực của tam giác \(ABC.\)
\(AO \bot BC\)
\(AO\) là tia phân giác của góc \(A.\)
Cho \(\Delta ABC\), hai đường cao $BD$ và $CE.$ Gọi $M$ là trung điểm của $BC.$ Em hãy chọn câu sai:
\(BM = MC\)
\(ME = MD\)
\(DM = MB\)
$M$ không thuộc đường trung trực của DE.
Cho \(\Delta ABC\) vuông tại $A,$ có \(\widehat C = {30^0}\), đường trung trực của $BC$ cắt $AC$ tại $M.$ Em hãy chọn câu đúng:
$BM$ là đường trung tuyến của \(\Delta ABC\)
\(BM = AB\).
$BM$ là phân giác của \(\widehat {ABC}\).
$BM$ là đường trung trực của \(\Delta ABC\).
Cho \(\Delta ABC\) cân ở $A.$ Đường trung trực của $AC$ cắt $AB$ ở $D.$ Biết $CD$ là tia phân giác của \(\widehat {ACB}\) . Tính các góc của \(\Delta ABC\).
\(\widehat A = {30^0},\widehat B = \widehat C = {75^0}\)
\(\widehat A = {40^0},\widehat B = \widehat C = {70^0}\)
\(\widehat A = {36^0},\widehat B = \widehat C = {72^0}\)
\(\widehat A = {70^0},\widehat B = \widehat C = {55^0}\).
Cho \(\Delta ABC\) cân tại $A,$ có \(\widehat A = {40^0}\), đường trung trực của $AB$ cắt $BC$ ở $D.$ Tính \(\widehat {CAD}\).
\({30^0}\)
\({45^0}\)
\({60^0}\)
\({40^0}\).
Nếu một tam giác có một đường trung tuyến đồng thời là đường trung trực thì tam giác đó là tam giác gì?
Tam giác vuông
Tam giác cân
Tam giác đều
Tam giác vuông cân
Gọi $O$ là giao điểm của ba đường trung trực trong \(\Delta ABC\). Khi đó $O$ là:
Điểm cách đều ba cạnh của \(\Delta ABC\).
Điểm cách đều ba đỉnh của \(\Delta ABC\).
Tâm đường tròn ngoại tiếp \(\Delta ABC\).
Đáp án B và C đúng
Lời giải và đáp án
Cho tam giác \(ABC\) có \(\widehat A\) là góc tù. Tia phân giác của góc \(B\) và góc \(C\) cắt nhau tại \(O.\) Lấy điểm \(E\) trên cạnh \(AB.\) Từ \(E\) kẻ \(EP \bot BO\,\,\left( {P \in BC} \right).\) Từ \(P\) kẻ \(PF \bot OC\,\left( {F \in AC} \right).\)
Chọn câu đúng.
\(OB\) là đường trung trực của đoạn \(EP\)
\(OC\) là đường trung trực của đoạn \(PF\)
Cả A, B đều đúng
Cả A,B đều sai
Đáp án: C
+ Chứng minh \(\Delta BME = \Delta BMP\); \(\Delta CNF = \Delta CNP\), từ đó suy ra các cạnh tương ứng bằng nhau.
+ Sử dụng định nghĩa đường trung trực của đoạn thẳng: “Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng ấy tại trung điểm của nó” để đưa ra đáp án đúng.
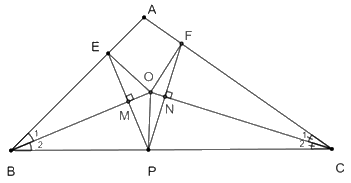
Giả sử \(EP \bot BO\) tại \(M\); \(PF \bot OC\) tại \(N\).
Khi đó \(\widehat {BME} = \widehat {BMP} = {90^0}\); \(\widehat {CNF} = \widehat {PNC} = {90^0}\)
Vì \(BO\) là tia phân giác của \(\widehat {ABC}\) (gt) nên \(\widehat {{B_1}} = \widehat {{B_2}}\) (tính chất tia phân giác)
Xét \(\Delta BME\) và \(\Delta BMP\) có:
\(\widehat {BME} = \widehat {BMP} = {90^0}\) (cmt)
\(BM\) là cạnh chung
\(\widehat {{B_1}} = \widehat {{B_2}}\) (cmt)
Do đó \(\Delta BME = \Delta BMP\) (g.c.g) suy ra \(ME = MP\) (hai cạnh tương ứng)
Mặt khác: \(EP \bot BO\) (gt)
Vậy \(OB\) là đường trung trực của đoạn \(EP\) (định nghĩa đường trung trực của đoạn thẳng). Đáp án A đúng.
Chứng minh tương tự ta có: \(\Delta CNF = \Delta CNP\) (g.c.g) suy ra \(NF = NP\) (hai cạnh tương ứng)
Mặt khác \(PF \bot OC\) (gt)
Vậy \(OC\) là đường trung trực của đoạn \(PF\) (định nghĩa đường trung trực của đoạn thẳng). Đáp án B đúng
So sánh \(BE + CF\) và \(BC.\)
\(BE + CF > BC\)
\(BE + CF < BC\)
\(BE + CF = BC\)
\(BE + CF = \dfrac{1}{2}BC\)
Đáp án: C
Chứng minh \(BE = BP\); \(CF = CP\), từ đó so sánh được \(BE + CF\) với \(BC.\)
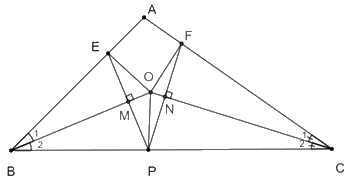
Theo câu trước ta có: \(\Delta BME = \Delta BMP\) (g.c.g) suy ra \(BE = BP\) (hai cạnh tương ứng)
Theo câu trước ta có: \(\Delta CNF = \Delta CNP\) (g.c.g) suy ra \(CF = CP\) (hai cạnh tương ứng)
Khi đó \(BE + CF = BP + CP = BC\).
Cho \(\Delta ABC\) nhọn, đường cao $AH.$ Lấy điểm $D$ sao cho $AB$ là trung trực của $HD.$ Lấy điểm $E$ sao cho $AC$ là trung trực của $HE.$ Gọi $M$ là giao điểm của $DE$ với $AB,N$ là giao điểm của $DE$ với $AC.$ Chọn câu đúng.
\(\Delta ADE\) là tam giác cân
$HA$ là tia phân giác của \(\widehat {MHN}\).
A, B đều đúng
A, B đều sai
Đáp án : C
Áp dụng tính chất đường trung trực của đoạn thẳng và tính chất hai tam giác bằng nhau..
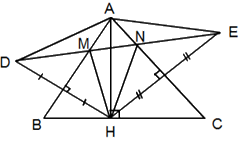
Vì $AB$ là đường trung trực của $HD$ (gt) \( \Rightarrow AD = AH\) (tính chất trung trực của đoạn thẳng)
Vì $AC$ là đường trung trực của $HE$ (gt) \( \Rightarrow AH = AE\) (tính chất trung trực của đoạn thẳng)
\( \Rightarrow AD = AE \Rightarrow \Delta ADE\) cân tại $A.$ Nên A đúng.
+) $M$ nằm trên đường trung trực của $HD$ nên $MD = MH$ (tính chất trung trực của đoạn thẳng)
Xét \(\Delta AMD\) và \(\Delta AMH\) có:
\(\)$AM$ chung.
$AD = AH$ (cmt)
$MD = MH$ (cmt)
\( \Rightarrow \Delta AMD = \Delta AMH\left( {c - c - c} \right) \Rightarrow \widehat {MDA} = \widehat {MHA}\) (2 góc tương ứng)
Lại có, $N$ thuộc đường trung trực của $HE$ nên $NH = NE$ (tính chất trung trực của đoạn thẳng).
+) Xét \(\Delta AHN\) và \(\Delta AEN\) có:
$AN$ chung
$AH = AE$ (cmt)
$NH = NE$ (cmt)
\( \Rightarrow \Delta AHN = \Delta AEN\left( {c - c - c} \right) \Rightarrow \widehat {NHA} = \widehat {NEA}\) (2 góc tương ứng)
Mà \(\Delta ADE\) cân tại $A$ (cmt) \( \Rightarrow \widehat {MDA} = \widehat {NEA} \Rightarrow \widehat {MHA} = \widehat {NHA}\) . Vậy $HA$ là đường phân giác của \(\widehat {MHN}\) .
Cho tam giác $ABC$ vuông tại $A,$ kẻ đường cao $AH.$ Trên cạnh $AC$ lấy điểm $K$ sao cho $AK = AH.$ Kẻ \(KD \bot AC\left( {D \in BC} \right)\). Chọn câu đúng.
\(\Delta AHD = \Delta AKD\)
$AD$ là đường trung trực của đoạn thẳng $HK.$
\(AD\) là tia phân giác của góc \(HAK.\)
Cả A, B, C đều đúng.
Đáp án : D
+ Chứng minh hai tam giác bằng nhau theo trường hợp cạnh huyền-cạnh góc vuông
+ Sử dụng tính chất hai tam giác bằng nhau để chứng minh \(AD\) là tia phân giác của góc \(HAK.\)
+ Sử dụng định lý về đường trung trực để chỉ ra $AD$ là đường trung trực của đoạn thẳng $HK.$
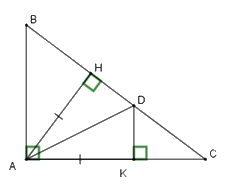
Xét tam giác vuông \(AHD\) và tam giác vuông \(AKD\) có
+ \(AH = AK\,\left( {gt} \right)\)
+ \(AD\) chung
Suy ra \(\Delta AHD = \Delta AKD\left( {ch - cgv} \right)\) nên A đúng
Từ đó ta có \(HD = DK;\,\widehat {HAD} = \widehat {DAK}\) suy ra \(AD\) là tia phân giác góc \(HAK\) nên C đúng.
Ta có \(AH = AK\left( {gt} \right)\) và \(HA = DK\left( {cmt} \right)\) suy ra \(AD\) là đường trung trực đoạn \(HK\) nên B đúng.
Vậy cả A, B, C đều đúng.
Cho tam giác \(ABC\) trong đó \(\widehat A = 100^\circ \). Các đường trung trực của \(AB\) và \(AC\) cắt cạnh \(BC\) theo thứ tự ở \(E\) và \(F\) . Tính \(\widehat {EAF}.\)
\(20^\circ \)
\(30^\circ \)
\(40^\circ \)
\(50^\circ \)
Đáp án : A
+ Sử dụng tính chất đường trung trực
+ Sử dụng tính chất tam giác cân để tính góc \(EAF.\)
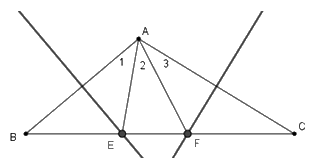
Ta có \(EA = EB\) nên \(\widehat {{A_1}} = \widehat B\) , \(FA = FC\) nên \(\widehat {{A_3}} = \widehat C\). Do đó \(\widehat {{A_1}} + \widehat {{A_3}} = \widehat B + \widehat C = 180^\circ - 100^\circ = 80^\circ \)
Suy ra \(\widehat {{A_2}} = 100^\circ - 80^\circ = 20^\circ .\)
Cho tam giác \(ABC\) có \(AC > AB.\) Trên cạnh \(AC\) lấy điểm \(E\) sao cho \(CE = AB.\) Các đường trung trực của \(BE\) và \(AC\) cắt nhau tại \(O.\)
Chọn câu đúng.
\(\Delta ABO = \Delta COE\)
\(\Delta BOA = \Delta COE\)
\(\Delta AOB = \Delta COE\)
\(\Delta ABO = \Delta CEO\)
Đáp án: C
+ Sử dụng tính chất đường trung trực của đoạn thẳng
+ Chứng minh hai tam giác bằng nhau theo trường hợp cạnh-cạnh –cạnh
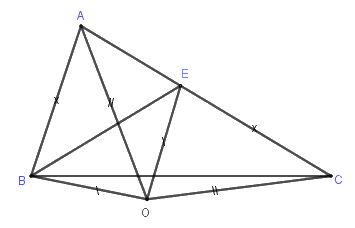
Xét tam giác \(AOB\) và \(COE\) có
+ \(OA = OC\) (vì $O$ thuộc đường trung trực của \(AC\))
+ \(OB = OE\) (vì $O$ thuộc đường trung trực của \(BE\))
+ \(AB = CE\) (giả thiết)
Do đó \(\Delta AOB = \Delta COE\left( {c - c - c} \right)\)
Chọn câu đúng
\(AO\) là đường trung tuyến của tam giác \(ABC.\)
\(AO\) là đường trung trực của tam giác \(ABC.\)
\(AO \bot BC\)
\(AO\) là tia phân giác của góc \(A.\)
Đáp án: D
+ Sử dụng tính chất hai tam giác bằng nhau và định nghĩa đường phân giác của một góc
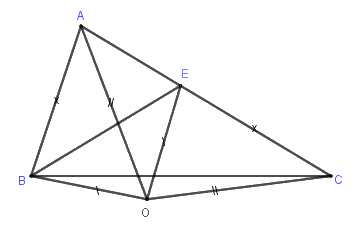
Ta có \(\Delta AOB = \Delta COE \Rightarrow \widehat {OAB} = \widehat {OCE}\,\,\left( 1 \right)\)
\(\Delta AOC\) cân tại \(O \Rightarrow \widehat {OAC} = \widehat {OCE}\,\,\left( 2 \right)\)
Từ \(\left( 1 \right);\left( 2 \right)\) suy ra \(\widehat {OAB} = \widehat {OAC}\) , do đó \(AO\) là tia phân giác góc \(A.\)
Cho \(\Delta ABC\), hai đường cao $BD$ và $CE.$ Gọi $M$ là trung điểm của $BC.$ Em hãy chọn câu sai:
\(BM = MC\)
\(ME = MD\)
\(DM = MB\)
$M$ không thuộc đường trung trực của DE.
Đáp án : D
Áp dụng tính chất trung điểm của đoạn thẳng, tính chất trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy.
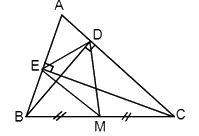
Vì $M$ là trung điểm của $BC$ (gt) suy ra $BM = MC$ (tính chất trung điểm), loại đáp án A.
Xét \({\Delta _v}BCE\)có $M$ là trung điểm của $BC$ (gt) suy ra $EM$ là trung tuyến.
\( \Rightarrow EM = \dfrac{{BC}}{2}\left( 1 \right)\) (trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy)
Xét \({\Delta _v}BCD\)có $M$ là trung điểm của $BC\left( {gt} \right)$ suy ra $DM$ là trung tuyến.
\( \Rightarrow DM = MB = \dfrac{{BC}}{2}\left( 2 \right)\) (trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy) nên loại đáp án C.
Từ (1) và (2) \( \Rightarrow EM = DM \Rightarrow \) M thuộc đường trung trực của DE. Loại đáp án B, chọn đáp án D.
Cho \(\Delta ABC\) vuông tại $A,$ có \(\widehat C = {30^0}\), đường trung trực của $BC$ cắt $AC$ tại $M.$ Em hãy chọn câu đúng:
$BM$ là đường trung tuyến của \(\Delta ABC\)
\(BM = AB\).
$BM$ là phân giác của \(\widehat {ABC}\).
$BM$ là đường trung trực của \(\Delta ABC\).
Đáp án : C
Áp dụng tính chất tam giác cân, tính chất đường trung trực của đoạn thẳng, định lý tổng 3 góc trong tam giác
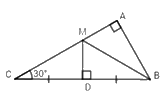
Vì $M$ thuộc đường trung trực của $BC$ \( \Rightarrow BM = MC\) (tính chất điểm thuộc đường trung trực của đoạn thẳng)
\( \Rightarrow \Delta BMC\) cân tại $M$ (dấu hiệu nhận biết tam giác cân)
\( \Rightarrow \widehat {MBC} = \widehat C = {30^0}\) (tính chất tam giác cân)
Xét \(\Delta ABC\) có: \(\widehat A + \widehat {ABC} + \widehat C = {180^0}\) (định lý tổng 3 góc trong tam giác)
\( \Rightarrow \widehat {ABC} = {180^0} - \widehat C - \widehat A = {180^0} - {30^0} - {90^0} = {60^0}\)
\( \Rightarrow \widehat {ABM} + \widehat {MBC} = \widehat {ABC} = {60^0} \Rightarrow \widehat {ABM} = {60^0} - \widehat {MBC} = {60^0} - {30^0} = {30^0}\)
\( \Rightarrow \widehat {ABM} = \widehat {MBC} \Rightarrow \) $BM$ là phân giác của \(\widehat {ABC}\).
Cho \(\Delta ABC\) cân ở $A.$ Đường trung trực của $AC$ cắt $AB$ ở $D.$ Biết $CD$ là tia phân giác của \(\widehat {ACB}\) . Tính các góc của \(\Delta ABC\).
\(\widehat A = {30^0},\widehat B = \widehat C = {75^0}\)
\(\widehat A = {40^0},\widehat B = \widehat C = {70^0}\)
\(\widehat A = {36^0},\widehat B = \widehat C = {72^0}\)
\(\widehat A = {70^0},\widehat B = \widehat C = {55^0}\).
Đáp án : C
Áp dụng tính chất tam giác cân, tính chất đường trung trực của đoạn thẳng, định lý tổng 3 góc trong tam giác.
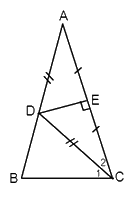
Vì đường trung trực của $AC$ cắt $AB$ tại $D$ nên suy ra \(DA = DC\)(tính chất đường trung trực của đoạn thẳng)
\( \Rightarrow \Delta ADC\) là tam giác cân tại $D$ (dấu hiệu nhận biết tam giác cân)
\( \Rightarrow \widehat A = \widehat {{C_2}}\,\left( 1 \right)\) (tính chất tam giác cân).
Vì $CD$ là đường phân giác của \(\widehat {ACB} \Rightarrow \widehat {{C_1}} = \widehat {{C_2}} = \dfrac{{\widehat C}}{2}\left( 2 \right)\) (tính chất tia phân giác).
Từ (1) và (2) \( \Rightarrow \widehat {ACB} = 2\widehat A\).
Lại có \(\Delta ABC\) cân tại $A$ (gt) \( \Rightarrow \widehat B = \widehat {ACB}\) (tính chất tam giác cân) \( \Rightarrow \widehat B = 2\widehat A\)
Xét \(\Delta ABC\) có:
$\widehat A + \widehat B + \widehat {ACB} = {180^0} \Rightarrow \widehat A + 2\widehat A + 2\widehat A = {180^0}$
$ \Rightarrow 5\widehat A = {180^0}$$ \Rightarrow \widehat A = {36^0} \Rightarrow \widehat B = \widehat C = 2\widehat A = {2.36^0} = {72^0}$
Vậy \(\widehat A = {36^0},\widehat B = \widehat C = {72^0}.\)
Cho \(\Delta ABC\) cân tại $A,$ có \(\widehat A = {40^0}\), đường trung trực của $AB$ cắt $BC$ ở $D.$ Tính \(\widehat {CAD}\).
\({30^0}\)
\({45^0}\)
\({60^0}\)
\({40^0}\).
Đáp án : A
Áp dụng tính chất đường trung trực của đoạn thẳng, tính chất tam giác cân.
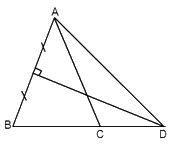
Vì \(\Delta ABC\) cân tại A (gt) \( \Rightarrow \widehat B = \widehat C = \left( {{{180}^0} - \widehat A} \right):2 = \left( {{{180}^0} - {{40}^0}} \right):2 = {70^0}.\)
Vì $D$ thuộc đường trung trực của $AB$ nên
\( \Rightarrow AD = BD\) (tính chất đường trung trực của đoạn thẳng)
\( \Rightarrow \Delta ABD\) cân tại $D$ (dấu hiệu nhận biết tam giác cân)
$ \Rightarrow \widehat {DAC} + \widehat {CAB} = \widehat {DAB} = \widehat B = {70^0} \Rightarrow \widehat {DAC} = {70^0} - \widehat {CAB} = {70^0} - {40^0} = {30^0}.$
Nếu một tam giác có một đường trung tuyến đồng thời là đường trung trực thì tam giác đó là tam giác gì?
Tam giác vuông
Tam giác cân
Tam giác đều
Tam giác vuông cân
Đáp án : B
Áp dụng tính chất đường trung trực và đường trung tuyến của tam giác.
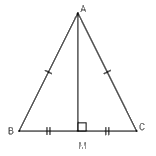
Giả sử \(\Delta ABC\) có $AM$ là trung tuyến đồng thời là đường trung trực. Ta sẽ chứng minh \(\Delta ABC\) là tam giác cân. Thật vậy, vì $AM$ là trung tuyến của \(\Delta ABC\) (gt) \( \Rightarrow BM = MC\) (tính chất trung tuyến)
Vì $AM$ là trung trực của $BC$ $ \Rightarrow AM \bot BC$
Xét hai tam giác vuông \({\Delta}ABM\) và \({\Delta}ACM\) có:
\(BM = CM\left( {cmt} \right)\)
$AM$ chung
nên \(\Delta ABM = \Delta ACM\) (2 cạnh góc vuông)
suy ra \(AB = AC\) (2 cạnh tương ứng)
Do đó \( \Delta ABC\) cân tại $A.$
Gọi $O$ là giao điểm của ba đường trung trực trong \(\Delta ABC\). Khi đó $O$ là:
Điểm cách đều ba cạnh của \(\Delta ABC\).
Điểm cách đều ba đỉnh của \(\Delta ABC\).
Tâm đường tròn ngoại tiếp \(\Delta ABC\).
Đáp án B và C đúng
Đáp án : D
Ba đường trung trực của một tam giác cùng đi qua 1 điểm. Điểm này cách đều ba đỉnh của tam giác và là tâm của đường tròn ngoại tiếp tam giác đó. Chọn đáp án D.
Cho tam giác \(ABC\) có \(\widehat A\) là góc tù. Tia phân giác của góc \(B\) và góc \(C\) cắt nhau tại \(O.\) Lấy điểm \(E\) trên cạnh \(AB.\) Từ \(E\) kẻ \(EP \bot BO\,\,\left( {P \in BC} \right).\) Từ \(P\) kẻ \(PF \bot OC\,\left( {F \in AC} \right).\)
Chọn câu đúng.
\(OB\) là đường trung trực của đoạn \(EP\)
\(OC\) là đường trung trực của đoạn \(PF\)
Cả A, B đều đúng
Cả A,B đều sai
So sánh \(BE + CF\) và \(BC.\)
\(BE + CF > BC\)
\(BE + CF < BC\)
\(BE + CF = BC\)
\(BE + CF = \dfrac{1}{2}BC\)
Cho \(\Delta ABC\) nhọn, đường cao $AH.$ Lấy điểm $D$ sao cho $AB$ là trung trực của $HD.$ Lấy điểm $E$ sao cho $AC$ là trung trực của $HE.$ Gọi $M$ là giao điểm của $DE$ với $AB,N$ là giao điểm của $DE$ với $AC.$ Chọn câu đúng.
\(\Delta ADE\) là tam giác cân
$HA$ là tia phân giác của \(\widehat {MHN}\).
A, B đều đúng
A, B đều sai
Cho tam giác $ABC$ vuông tại $A,$ kẻ đường cao $AH.$ Trên cạnh $AC$ lấy điểm $K$ sao cho $AK = AH.$ Kẻ \(KD \bot AC\left( {D \in BC} \right)\). Chọn câu đúng.
\(\Delta AHD = \Delta AKD\)
$AD$ là đường trung trực của đoạn thẳng $HK.$
\(AD\) là tia phân giác của góc \(HAK.\)
Cả A, B, C đều đúng.
Cho tam giác \(ABC\) trong đó \(\widehat A = 100^\circ \). Các đường trung trực của \(AB\) và \(AC\) cắt cạnh \(BC\) theo thứ tự ở \(E\) và \(F\) . Tính \(\widehat {EAF}.\)
\(20^\circ \)
\(30^\circ \)
\(40^\circ \)
\(50^\circ \)
Cho tam giác \(ABC\) có \(AC > AB.\) Trên cạnh \(AC\) lấy điểm \(E\) sao cho \(CE = AB.\) Các đường trung trực của \(BE\) và \(AC\) cắt nhau tại \(O.\)
Chọn câu đúng.
\(\Delta ABO = \Delta COE\)
\(\Delta BOA = \Delta COE\)
\(\Delta AOB = \Delta COE\)
\(\Delta ABO = \Delta CEO\)
Chọn câu đúng
\(AO\) là đường trung tuyến của tam giác \(ABC.\)
\(AO\) là đường trung trực của tam giác \(ABC.\)
\(AO \bot BC\)
\(AO\) là tia phân giác của góc \(A.\)
Cho \(\Delta ABC\), hai đường cao $BD$ và $CE.$ Gọi $M$ là trung điểm của $BC.$ Em hãy chọn câu sai:
\(BM = MC\)
\(ME = MD\)
\(DM = MB\)
$M$ không thuộc đường trung trực của DE.
Cho \(\Delta ABC\) vuông tại $A,$ có \(\widehat C = {30^0}\), đường trung trực của $BC$ cắt $AC$ tại $M.$ Em hãy chọn câu đúng:
$BM$ là đường trung tuyến của \(\Delta ABC\)
\(BM = AB\).
$BM$ là phân giác của \(\widehat {ABC}\).
$BM$ là đường trung trực của \(\Delta ABC\).
Cho \(\Delta ABC\) cân ở $A.$ Đường trung trực của $AC$ cắt $AB$ ở $D.$ Biết $CD$ là tia phân giác của \(\widehat {ACB}\) . Tính các góc của \(\Delta ABC\).
\(\widehat A = {30^0},\widehat B = \widehat C = {75^0}\)
\(\widehat A = {40^0},\widehat B = \widehat C = {70^0}\)
\(\widehat A = {36^0},\widehat B = \widehat C = {72^0}\)
\(\widehat A = {70^0},\widehat B = \widehat C = {55^0}\).
Cho \(\Delta ABC\) cân tại $A,$ có \(\widehat A = {40^0}\), đường trung trực của $AB$ cắt $BC$ ở $D.$ Tính \(\widehat {CAD}\).
\({30^0}\)
\({45^0}\)
\({60^0}\)
\({40^0}\).
Nếu một tam giác có một đường trung tuyến đồng thời là đường trung trực thì tam giác đó là tam giác gì?
Tam giác vuông
Tam giác cân
Tam giác đều
Tam giác vuông cân
Gọi $O$ là giao điểm của ba đường trung trực trong \(\Delta ABC\). Khi đó $O$ là:
Điểm cách đều ba cạnh của \(\Delta ABC\).
Điểm cách đều ba đỉnh của \(\Delta ABC\).
Tâm đường tròn ngoại tiếp \(\Delta ABC\).
Đáp án B và C đúng
Cho tam giác \(ABC\) có \(\widehat A\) là góc tù. Tia phân giác của góc \(B\) và góc \(C\) cắt nhau tại \(O.\) Lấy điểm \(E\) trên cạnh \(AB.\) Từ \(E\) kẻ \(EP \bot BO\,\,\left( {P \in BC} \right).\) Từ \(P\) kẻ \(PF \bot OC\,\left( {F \in AC} \right).\)
Chọn câu đúng.
\(OB\) là đường trung trực của đoạn \(EP\)
\(OC\) là đường trung trực của đoạn \(PF\)
Cả A, B đều đúng
Cả A,B đều sai
Đáp án: C
+ Chứng minh \(\Delta BME = \Delta BMP\); \(\Delta CNF = \Delta CNP\), từ đó suy ra các cạnh tương ứng bằng nhau.
+ Sử dụng định nghĩa đường trung trực của đoạn thẳng: “Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng ấy tại trung điểm của nó” để đưa ra đáp án đúng.

Giả sử \(EP \bot BO\) tại \(M\); \(PF \bot OC\) tại \(N\).
Khi đó \(\widehat {BME} = \widehat {BMP} = {90^0}\); \(\widehat {CNF} = \widehat {PNC} = {90^0}\)
Vì \(BO\) là tia phân giác của \(\widehat {ABC}\) (gt) nên \(\widehat {{B_1}} = \widehat {{B_2}}\) (tính chất tia phân giác)
Xét \(\Delta BME\) và \(\Delta BMP\) có:
\(\widehat {BME} = \widehat {BMP} = {90^0}\) (cmt)
\(BM\) là cạnh chung
\(\widehat {{B_1}} = \widehat {{B_2}}\) (cmt)
Do đó \(\Delta BME = \Delta BMP\) (g.c.g) suy ra \(ME = MP\) (hai cạnh tương ứng)
Mặt khác: \(EP \bot BO\) (gt)
Vậy \(OB\) là đường trung trực của đoạn \(EP\) (định nghĩa đường trung trực của đoạn thẳng). Đáp án A đúng.
Chứng minh tương tự ta có: \(\Delta CNF = \Delta CNP\) (g.c.g) suy ra \(NF = NP\) (hai cạnh tương ứng)
Mặt khác \(PF \bot OC\) (gt)
Vậy \(OC\) là đường trung trực của đoạn \(PF\) (định nghĩa đường trung trực của đoạn thẳng). Đáp án B đúng
So sánh \(BE + CF\) và \(BC.\)
\(BE + CF > BC\)
\(BE + CF < BC\)
\(BE + CF = BC\)
\(BE + CF = \dfrac{1}{2}BC\)
Đáp án: C
Chứng minh \(BE = BP\); \(CF = CP\), từ đó so sánh được \(BE + CF\) với \(BC.\)

Theo câu trước ta có: \(\Delta BME = \Delta BMP\) (g.c.g) suy ra \(BE = BP\) (hai cạnh tương ứng)
Theo câu trước ta có: \(\Delta CNF = \Delta CNP\) (g.c.g) suy ra \(CF = CP\) (hai cạnh tương ứng)
Khi đó \(BE + CF = BP + CP = BC\).
Cho \(\Delta ABC\) nhọn, đường cao $AH.$ Lấy điểm $D$ sao cho $AB$ là trung trực của $HD.$ Lấy điểm $E$ sao cho $AC$ là trung trực của $HE.$ Gọi $M$ là giao điểm của $DE$ với $AB,N$ là giao điểm của $DE$ với $AC.$ Chọn câu đúng.
\(\Delta ADE\) là tam giác cân
$HA$ là tia phân giác của \(\widehat {MHN}\).
A, B đều đúng
A, B đều sai
Đáp án : C
Áp dụng tính chất đường trung trực của đoạn thẳng và tính chất hai tam giác bằng nhau..

Vì $AB$ là đường trung trực của $HD$ (gt) \( \Rightarrow AD = AH\) (tính chất trung trực của đoạn thẳng)
Vì $AC$ là đường trung trực của $HE$ (gt) \( \Rightarrow AH = AE\) (tính chất trung trực của đoạn thẳng)
\( \Rightarrow AD = AE \Rightarrow \Delta ADE\) cân tại $A.$ Nên A đúng.
+) $M$ nằm trên đường trung trực của $HD$ nên $MD = MH$ (tính chất trung trực của đoạn thẳng)
Xét \(\Delta AMD\) và \(\Delta AMH\) có:
\(\)$AM$ chung.
$AD = AH$ (cmt)
$MD = MH$ (cmt)
\( \Rightarrow \Delta AMD = \Delta AMH\left( {c - c - c} \right) \Rightarrow \widehat {MDA} = \widehat {MHA}\) (2 góc tương ứng)
Lại có, $N$ thuộc đường trung trực của $HE$ nên $NH = NE$ (tính chất trung trực của đoạn thẳng).
+) Xét \(\Delta AHN\) và \(\Delta AEN\) có:
$AN$ chung
$AH = AE$ (cmt)
$NH = NE$ (cmt)
\( \Rightarrow \Delta AHN = \Delta AEN\left( {c - c - c} \right) \Rightarrow \widehat {NHA} = \widehat {NEA}\) (2 góc tương ứng)
Mà \(\Delta ADE\) cân tại $A$ (cmt) \( \Rightarrow \widehat {MDA} = \widehat {NEA} \Rightarrow \widehat {MHA} = \widehat {NHA}\) . Vậy $HA$ là đường phân giác của \(\widehat {MHN}\) .
Cho tam giác $ABC$ vuông tại $A,$ kẻ đường cao $AH.$ Trên cạnh $AC$ lấy điểm $K$ sao cho $AK = AH.$ Kẻ \(KD \bot AC\left( {D \in BC} \right)\). Chọn câu đúng.
\(\Delta AHD = \Delta AKD\)
$AD$ là đường trung trực của đoạn thẳng $HK.$
\(AD\) là tia phân giác của góc \(HAK.\)
Cả A, B, C đều đúng.
Đáp án : D
+ Chứng minh hai tam giác bằng nhau theo trường hợp cạnh huyền-cạnh góc vuông
+ Sử dụng tính chất hai tam giác bằng nhau để chứng minh \(AD\) là tia phân giác của góc \(HAK.\)
+ Sử dụng định lý về đường trung trực để chỉ ra $AD$ là đường trung trực của đoạn thẳng $HK.$

Xét tam giác vuông \(AHD\) và tam giác vuông \(AKD\) có
+ \(AH = AK\,\left( {gt} \right)\)
+ \(AD\) chung
Suy ra \(\Delta AHD = \Delta AKD\left( {ch - cgv} \right)\) nên A đúng
Từ đó ta có \(HD = DK;\,\widehat {HAD} = \widehat {DAK}\) suy ra \(AD\) là tia phân giác góc \(HAK\) nên C đúng.
Ta có \(AH = AK\left( {gt} \right)\) và \(HA = DK\left( {cmt} \right)\) suy ra \(AD\) là đường trung trực đoạn \(HK\) nên B đúng.
Vậy cả A, B, C đều đúng.
Cho tam giác \(ABC\) trong đó \(\widehat A = 100^\circ \). Các đường trung trực của \(AB\) và \(AC\) cắt cạnh \(BC\) theo thứ tự ở \(E\) và \(F\) . Tính \(\widehat {EAF}.\)
\(20^\circ \)
\(30^\circ \)
\(40^\circ \)
\(50^\circ \)
Đáp án : A
+ Sử dụng tính chất đường trung trực
+ Sử dụng tính chất tam giác cân để tính góc \(EAF.\)

Ta có \(EA = EB\) nên \(\widehat {{A_1}} = \widehat B\) , \(FA = FC\) nên \(\widehat {{A_3}} = \widehat C\). Do đó \(\widehat {{A_1}} + \widehat {{A_3}} = \widehat B + \widehat C = 180^\circ - 100^\circ = 80^\circ \)
Suy ra \(\widehat {{A_2}} = 100^\circ - 80^\circ = 20^\circ .\)
Cho tam giác \(ABC\) có \(AC > AB.\) Trên cạnh \(AC\) lấy điểm \(E\) sao cho \(CE = AB.\) Các đường trung trực của \(BE\) và \(AC\) cắt nhau tại \(O.\)
Chọn câu đúng.
\(\Delta ABO = \Delta COE\)
\(\Delta BOA = \Delta COE\)
\(\Delta AOB = \Delta COE\)
\(\Delta ABO = \Delta CEO\)
Đáp án: C
+ Sử dụng tính chất đường trung trực của đoạn thẳng
+ Chứng minh hai tam giác bằng nhau theo trường hợp cạnh-cạnh –cạnh

Xét tam giác \(AOB\) và \(COE\) có
+ \(OA = OC\) (vì $O$ thuộc đường trung trực của \(AC\))
+ \(OB = OE\) (vì $O$ thuộc đường trung trực của \(BE\))
+ \(AB = CE\) (giả thiết)
Do đó \(\Delta AOB = \Delta COE\left( {c - c - c} \right)\)
Chọn câu đúng
\(AO\) là đường trung tuyến của tam giác \(ABC.\)
\(AO\) là đường trung trực của tam giác \(ABC.\)
\(AO \bot BC\)
\(AO\) là tia phân giác của góc \(A.\)
Đáp án: D
+ Sử dụng tính chất hai tam giác bằng nhau và định nghĩa đường phân giác của một góc

Ta có \(\Delta AOB = \Delta COE \Rightarrow \widehat {OAB} = \widehat {OCE}\,\,\left( 1 \right)\)
\(\Delta AOC\) cân tại \(O \Rightarrow \widehat {OAC} = \widehat {OCE}\,\,\left( 2 \right)\)
Từ \(\left( 1 \right);\left( 2 \right)\) suy ra \(\widehat {OAB} = \widehat {OAC}\) , do đó \(AO\) là tia phân giác góc \(A.\)
Cho \(\Delta ABC\), hai đường cao $BD$ và $CE.$ Gọi $M$ là trung điểm của $BC.$ Em hãy chọn câu sai:
\(BM = MC\)
\(ME = MD\)
\(DM = MB\)
$M$ không thuộc đường trung trực của DE.
Đáp án : D
Áp dụng tính chất trung điểm của đoạn thẳng, tính chất trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy.

Vì $M$ là trung điểm của $BC$ (gt) suy ra $BM = MC$ (tính chất trung điểm), loại đáp án A.
Xét \({\Delta _v}BCE\)có $M$ là trung điểm của $BC$ (gt) suy ra $EM$ là trung tuyến.
\( \Rightarrow EM = \dfrac{{BC}}{2}\left( 1 \right)\) (trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy)
Xét \({\Delta _v}BCD\)có $M$ là trung điểm của $BC\left( {gt} \right)$ suy ra $DM$ là trung tuyến.
\( \Rightarrow DM = MB = \dfrac{{BC}}{2}\left( 2 \right)\) (trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy) nên loại đáp án C.
Từ (1) và (2) \( \Rightarrow EM = DM \Rightarrow \) M thuộc đường trung trực của DE. Loại đáp án B, chọn đáp án D.
Cho \(\Delta ABC\) vuông tại $A,$ có \(\widehat C = {30^0}\), đường trung trực của $BC$ cắt $AC$ tại $M.$ Em hãy chọn câu đúng:
$BM$ là đường trung tuyến của \(\Delta ABC\)
\(BM = AB\).
$BM$ là phân giác của \(\widehat {ABC}\).
$BM$ là đường trung trực của \(\Delta ABC\).
Đáp án : C
Áp dụng tính chất tam giác cân, tính chất đường trung trực của đoạn thẳng, định lý tổng 3 góc trong tam giác

Vì $M$ thuộc đường trung trực của $BC$ \( \Rightarrow BM = MC\) (tính chất điểm thuộc đường trung trực của đoạn thẳng)
\( \Rightarrow \Delta BMC\) cân tại $M$ (dấu hiệu nhận biết tam giác cân)
\( \Rightarrow \widehat {MBC} = \widehat C = {30^0}\) (tính chất tam giác cân)
Xét \(\Delta ABC\) có: \(\widehat A + \widehat {ABC} + \widehat C = {180^0}\) (định lý tổng 3 góc trong tam giác)
\( \Rightarrow \widehat {ABC} = {180^0} - \widehat C - \widehat A = {180^0} - {30^0} - {90^0} = {60^0}\)
\( \Rightarrow \widehat {ABM} + \widehat {MBC} = \widehat {ABC} = {60^0} \Rightarrow \widehat {ABM} = {60^0} - \widehat {MBC} = {60^0} - {30^0} = {30^0}\)
\( \Rightarrow \widehat {ABM} = \widehat {MBC} \Rightarrow \) $BM$ là phân giác của \(\widehat {ABC}\).
Cho \(\Delta ABC\) cân ở $A.$ Đường trung trực của $AC$ cắt $AB$ ở $D.$ Biết $CD$ là tia phân giác của \(\widehat {ACB}\) . Tính các góc của \(\Delta ABC\).
\(\widehat A = {30^0},\widehat B = \widehat C = {75^0}\)
\(\widehat A = {40^0},\widehat B = \widehat C = {70^0}\)
\(\widehat A = {36^0},\widehat B = \widehat C = {72^0}\)
\(\widehat A = {70^0},\widehat B = \widehat C = {55^0}\).
Đáp án : C
Áp dụng tính chất tam giác cân, tính chất đường trung trực của đoạn thẳng, định lý tổng 3 góc trong tam giác.

Vì đường trung trực của $AC$ cắt $AB$ tại $D$ nên suy ra \(DA = DC\)(tính chất đường trung trực của đoạn thẳng)
\( \Rightarrow \Delta ADC\) là tam giác cân tại $D$ (dấu hiệu nhận biết tam giác cân)
\( \Rightarrow \widehat A = \widehat {{C_2}}\,\left( 1 \right)\) (tính chất tam giác cân).
Vì $CD$ là đường phân giác của \(\widehat {ACB} \Rightarrow \widehat {{C_1}} = \widehat {{C_2}} = \dfrac{{\widehat C}}{2}\left( 2 \right)\) (tính chất tia phân giác).
Từ (1) và (2) \( \Rightarrow \widehat {ACB} = 2\widehat A\).
Lại có \(\Delta ABC\) cân tại $A$ (gt) \( \Rightarrow \widehat B = \widehat {ACB}\) (tính chất tam giác cân) \( \Rightarrow \widehat B = 2\widehat A\)
Xét \(\Delta ABC\) có:
$\widehat A + \widehat B + \widehat {ACB} = {180^0} \Rightarrow \widehat A + 2\widehat A + 2\widehat A = {180^0}$
$ \Rightarrow 5\widehat A = {180^0}$$ \Rightarrow \widehat A = {36^0} \Rightarrow \widehat B = \widehat C = 2\widehat A = {2.36^0} = {72^0}$
Vậy \(\widehat A = {36^0},\widehat B = \widehat C = {72^0}.\)
Cho \(\Delta ABC\) cân tại $A,$ có \(\widehat A = {40^0}\), đường trung trực của $AB$ cắt $BC$ ở $D.$ Tính \(\widehat {CAD}\).
\({30^0}\)
\({45^0}\)
\({60^0}\)
\({40^0}\).
Đáp án : A
Áp dụng tính chất đường trung trực của đoạn thẳng, tính chất tam giác cân.

Vì \(\Delta ABC\) cân tại A (gt) \( \Rightarrow \widehat B = \widehat C = \left( {{{180}^0} - \widehat A} \right):2 = \left( {{{180}^0} - {{40}^0}} \right):2 = {70^0}.\)
Vì $D$ thuộc đường trung trực của $AB$ nên
\( \Rightarrow AD = BD\) (tính chất đường trung trực của đoạn thẳng)
\( \Rightarrow \Delta ABD\) cân tại $D$ (dấu hiệu nhận biết tam giác cân)
$ \Rightarrow \widehat {DAC} + \widehat {CAB} = \widehat {DAB} = \widehat B = {70^0} \Rightarrow \widehat {DAC} = {70^0} - \widehat {CAB} = {70^0} - {40^0} = {30^0}.$
Nếu một tam giác có một đường trung tuyến đồng thời là đường trung trực thì tam giác đó là tam giác gì?
Tam giác vuông
Tam giác cân
Tam giác đều
Tam giác vuông cân
Đáp án : B
Áp dụng tính chất đường trung trực và đường trung tuyến của tam giác.

Giả sử \(\Delta ABC\) có $AM$ là trung tuyến đồng thời là đường trung trực. Ta sẽ chứng minh \(\Delta ABC\) là tam giác cân. Thật vậy, vì $AM$ là trung tuyến của \(\Delta ABC\) (gt) \( \Rightarrow BM = MC\) (tính chất trung tuyến)
Vì $AM$ là trung trực của $BC$ $ \Rightarrow AM \bot BC$
Xét hai tam giác vuông \({\Delta}ABM\) và \({\Delta}ACM\) có:
\(BM = CM\left( {cmt} \right)\)
$AM$ chung
nên \(\Delta ABM = \Delta ACM\) (2 cạnh góc vuông)
suy ra \(AB = AC\) (2 cạnh tương ứng)
Do đó \( \Delta ABC\) cân tại $A.$
Gọi $O$ là giao điểm của ba đường trung trực trong \(\Delta ABC\). Khi đó $O$ là:
Điểm cách đều ba cạnh của \(\Delta ABC\).
Điểm cách đều ba đỉnh của \(\Delta ABC\).
Tâm đường tròn ngoại tiếp \(\Delta ABC\).
Đáp án B và C đúng
Đáp án : D
Ba đường trung trực của một tam giác cùng đi qua 1 điểm. Điểm này cách đều ba đỉnh của tam giác và là tâm của đường tròn ngoại tiếp tam giác đó. Chọn đáp án D.
Bài 12 trong chương trình Toán 7 Cánh diều tập trung vào một trong những tính chất quan trọng nhất của hình học tam giác: tính chất ba đường trung trực. Hiểu rõ tính chất này không chỉ giúp giải quyết các bài toán liên quan đến tam giác mà còn là nền tảng cho các kiến thức hình học nâng cao hơn.
Trước khi đi vào phần trắc nghiệm, chúng ta cùng ôn lại một số kiến thức cơ bản. Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng đó tại trung điểm của nó. Mọi điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
Giao điểm của ba đường trung trực của một tam giác là tâm đường tròn ngoại tiếp tam giác đó. Tâm đường tròn ngoại tiếp tam giác là điểm cách đều ba đỉnh của tam giác. Điều này có nghĩa là, nếu gọi O là giao điểm của ba đường trung trực, thì OA = OB = OC, với A, B, C là ba đỉnh của tam giác.
Các câu hỏi thuộc dạng này thường yêu cầu học sinh xác định đường trung trực của một cạnh trong tam giác, hoặc tìm tâm đường tròn ngoại tiếp tam giác khi biết một số thông tin về tam giác đó.
Dạng bài này đòi hỏi học sinh phải vận dụng tính chất đường trung trực để chứng minh các đẳng thức, tính độ dài đoạn thẳng, hoặc giải các bài toán liên quan đến góc.
Đây là dạng bài khó hơn, kết hợp kiến thức về đường trung trực với các kiến thức khác trong chương trình Toán 7, như tam giác cân, tam giác đều, các dấu hiệu nhận biết tam giác cân, tam giác đều.
Dưới đây là một số câu hỏi trắc nghiệm minh họa:
(Đáp án: B)
(Đáp án: D)
(Đáp án: B)
Việc nắm vững tính chất ba đường trung trực của tam giác là rất quan trọng trong chương trình Toán 7. Hy vọng với bộ câu hỏi trắc nghiệm này, các em học sinh sẽ có thêm công cụ để ôn luyện và củng cố kiến thức. Chúc các em học tập tốt và đạt kết quả cao trong các kỳ thi!