Bài viết này cung cấp bộ câu hỏi trắc nghiệm Bài 7: Tam giác cân Toán 7 Cánh diều, được thiết kế để giúp học sinh ôn tập và củng cố kiến thức một cách hiệu quả. Chúng tôi tập trung vào việc cung cấp các dạng bài tập đa dạng, bao gồm cả lý thuyết và ứng dụng thực tế.
Với đáp án chi tiết và lời giải dễ hiểu, các em có thể tự đánh giá năng lực của mình và tìm ra những điểm cần cải thiện.
Cho tam giác \(ABC\) cân tại \(A\) có: \(\widehat A = {100^0}, BC = a, AC = b.\) Về phía ngoài tam giác \(ABC\) vẽ tam giác \(ABD\) cân tại \(D\) có: \(\widehat {ADB} = {140^0}.\) Tính chu vi tam giác \(ABD\) theo \(a\) và \(b.\)
\(2a + b\)
\(a - b\)
\(2a - b\)
\(2a - 2b\)
Cho tam giác \(ABC\) cân tại \(A\) có \(\widehat A = {120^0},BC = 6cm.\) Đường vuông góc với \(AB\) tại \(A\) cắt \(BC\) ở \(D.\) Độ dài \(BD\) bằng:
\(2\,cm\)
\(3\,cm\)
\(4\,cm\)
\(5\,cm\)
Cho tam giác \(ABC\) vuông tại \(A\) có \(\widehat B = {30^0}.\) Khi đó:
\(AC = \dfrac{{BC}}{2}\)
\(AB = \dfrac{{BC}}{2}\)
\(\Delta ABC\) là tam giác vuông cân
\(AC = \dfrac{{BC}}{3}\)
Cho \(M\) thuộc đoạn thẳng \(AB.\) Trên cùng một nửa mặt phẳng bờ \(AB,\) vẽ các tam giác đều \(AMC,BMD.\) Gọi \(E;F\) theo thứ tự là trung điểm của \(AD;BC.\) Tam giác \(MEF\) là tam giác gì? Chọn câu trả lời đúng nhất.
Tam giác nhọn
Tam giác cân
Tam giác đều
Cả A, B, C đều đúng
Cho tam giác $ABC$ có \(\widehat A = {60^ \circ }\). Vẽ ra phía ngoài của tam giác hai tam giác đều $AMB$ và $ANC.$
Ba điểm $M,A,N$ thẳng hàng.
$BN = CM$
Cả A, B đều sai
Cả A, B đều đúng
Cho tam giác \(ABC\) có \(\widehat A = 120^\circ .\) Trên tia phân giác của góc \(A\) lấy điểm \(D\) sao cho \(AD = AB + AC.\) Khi đó tam giác \(BCD\) là tam giác gì?
cân
đều
vuông
vuông cân
Tam giác \(ABC\) có \(\widehat A = 40^\circ ;\,\widehat B - \widehat C = 20^\circ .\) Trên tia đối của tia \(AC\) lấy điểm \(E\) sao cho \(AE = AB.\) Tính số đo góc \(CBE.\)
\(80^\circ \)
\(100^\circ \)
\(90^\circ \)
\(120^\circ \)
Cho tam giác \(ABC\) có \(M\) là trung điểm của \(BC\) và \(AM = \dfrac{{BC}}{2}\). Số đo góc \(BAC\) là
\(45^\circ \)
\(30^0\)
\(90^\circ \)
\(60^\circ \)
Cho tam giác \(ABC\) có \(\widehat A = 90^\circ ;\,AB = AC\). Khi đó
\(\Delta ABC\) là tam giác vuông
\(\Delta ABC\) là tam giác cân
\(\Delta ABC\) là tam giác vuông cân
Cả A, B, C đều đúng.
Cho tam giác $ABC$ cân tại đỉnh $A$ với \(\widehat A = {80^0}\). Trên hai cạnh $AB,AC$ lần lượt lấy hai điểm $D$ và $E$ sao cho $AD = AE.$ Phát biểu nào sau đây là sai?
$DE//BC$
\(\widehat B = {50^0}\)
\(\widehat {ADE} = {50^0}\)
Cả ba phát biểu trên đều sai
Cho tam giác $ABC$ vuông cân ở $A.$ Trên đáy $BC$ lấy hai điểm $M,N$ sao cho $BM = CN = AB.$
Tam giác \(AMN\) là tam giác gì?
cân
vuông cân
đều
vuông
Tính số đo góc \(\widehat {MAN.}\)
\(45^\circ \)
\(30^\circ \)
\(90^\circ \)
\(60^\circ \)
Tính số đo \(x\) trên hình vẽ sau:
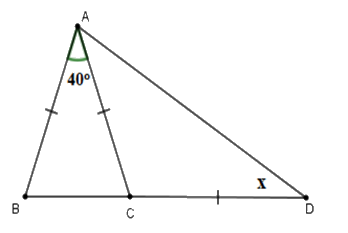
\(x = 45^\circ .\)
\(x = 40^\circ .\)
\(x = 35^\circ .\)
\(x = 70^\circ .\)
Số tam giác cân trong hình vẽ dưới đây là:
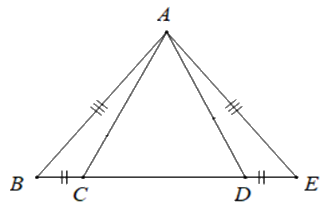
\(2\)
\(1\)
\(3\)
\(4\)
Một tam giác cân có góc ở đáy bằng \({70^0}\) thì số đo góc ở đỉnh là:
\({54^0}\)
\({63^0}\)
\({70^0}\)
\({40^0}\)
Một tam giác cân có góc ở đỉnh bằng \({64^0}\) thì số đo góc ở đáy là:
\({54^0}\)
\({58^0}\)
\({72^0}\)
\({90^0}\)
Cho tam giác $ABC$ cân tại $A.$ Phát biểu nào trong các phát biểu sau là sai:
\(\widehat B = \widehat C\)
\(\widehat C = \dfrac{{{{180}^0} - \widehat A}}{2}\)
\(\widehat A = {180^0} - 2\widehat C\)
\(\widehat B \ne \widehat C\)
Hai góc nhọn của tam giác vuông cân bằng nhau và bằng
\(30^\circ \)
\(45^\circ \)
\(60^\circ \)
\(90^\circ \)
Chọn câu sai.
Tam giác đều có ba góc bằng nhau và bằng \(60^\circ .\)
Tam giác đều có ba cạnh bằng nhau.
Tam giác cân là tam giác đều.
Tam giác đều là tam giác cân.
Lời giải và đáp án
Cho tam giác \(ABC\) cân tại \(A\) có: \(\widehat A = {100^0}, BC = a, AC = b.\) Về phía ngoài tam giác \(ABC\) vẽ tam giác \(ABD\) cân tại \(D\) có: \(\widehat {ADB} = {140^0}.\) Tính chu vi tam giác \(ABD\) theo \(a\) và \(b.\)
\(2a + b\)
\(a - b\)
\(2a - b\)
\(2a - 2b\)
Đáp án : C
- Trên cạnh \(BC\) lấy điểm \(E\) sao cho \(BE = BD.\)
- Chứng minh \(\Delta BDE\) đều, suy ra \(BD = BE = DE = DA.\)
- Chứng minh \(\Delta CAE\) cân tại \(C\), suy ra \(AC = EC.\)
- Biểu diễn \(AD;\,BD;\,AB\) theo \(a,\,b.\) Từ đó tính chu vi của \(\Delta ABD\).
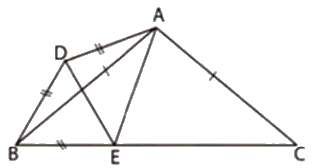
Trên cạnh \(BC\) lấy điểm \(E\) sao cho \(BE = BD.\)
\(\Delta ABC\) cân tại \(A\) nên \(\widehat {ABC} = \dfrac{{{{180}^o} - \widehat {BAC}}}{2} = \dfrac{{{{180}^o} - {{100}^o}}}{2} = {40^o}.\)
\(\Delta ABD\) cân tại \(D\) nên \(\widehat {DBA} = \dfrac{{{{180}^o} - \widehat {ADB}}}{2} = \dfrac{{{{180}^o} - {{140}^o}}}{2} = {20^o}\).
Ta có: \(\widehat {DBE} = \widehat {DBA} + \widehat {ABC} = {20^o} + {40^o} = {60^o}.\)
Xét \(\Delta BDE\) có: \(\widehat {DBE} = {60^o}\) nên \(\Delta BDE\) đều, suy ra \(BD = BE = DE = DA.\)
\(\widehat {EDA} = \widehat {BDA} - \widehat {BDE} = {140^o} - {60^o} = {80^o}\)
\(\Delta DAE\) cân tại \(D\) (vì \(DA = DE\,(cmt)\)) nên \(\widehat {DEA} = \widehat {DAE} = \dfrac{{{{180}^o} - \widehat {EDA}}}{2} = \dfrac{{{{180}^o} - {{80}^o}}}{2} = {50^o}.\)
\(\widehat {EAC} = \widehat {DAB} + \widehat {BAC} - \widehat {DAE} = {20^o} + {100^o} - {50^o} = {70^o}.\)
\(\widehat {AEC} = {180^o} - \widehat {DEA} - \widehat {DEB} = {180^o} - {50^o} - {60^o} = {70^o}.\)
\(\Delta CAE\) có \(\widehat {EAC} = \widehat {AEC} = {70^o}\) nên \(\Delta CAE\) cân tại \(C\), suy ra \(AC = EC.\)
Do đó: \(AD = BD = BE = BC - EC = BC - AC = a - b.\)
\(AB = AC = b.\)
Vậy chu vi của \(\Delta ABD\) là:
\(AD + BD + AB = a - b + a - b + b = 2a - b.\)
Cho tam giác \(ABC\) cân tại \(A\) có \(\widehat A = {120^0},BC = 6cm.\) Đường vuông góc với \(AB\) tại \(A\) cắt \(BC\) ở \(D.\) Độ dài \(BD\) bằng:
\(2\,cm\)
\(3\,cm\)
\(4\,cm\)
\(5\,cm\)
Đáp án : C
- Chứng minh \(\Delta ADC\) cân tại \(D\), suy ra \(DC = DA\) (1)
- Trên cạnh \(BD\) lấy \(E\) sao cho \(\widehat {BAE} = {30^o}\), chứng minh \(\Delta AEB\) cân tại \(E\), suy ra \(AE = EB\) (2)
- Chứng minh \(\Delta ADE\) là tam giác đều, suy ra \(DA = DE = AE\) (3)
- Từ (1), (2) và (3) suy ra: \(DC = DE = EB = \dfrac{1}{3}BC\), từ đó ta tính được độ dài \(BD.\)
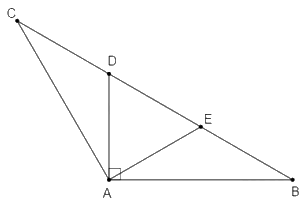
\(\Delta ABC\) cân tại \(\widehat A\) nên \(\widehat B = \widehat C = \dfrac{{{{180}^o} - \widehat A}}{2} = \dfrac{{{{180}^o} - {{120}^o}}}{2} = {30^o}.\)
Ta có: \(\widehat {CAD} = \widehat {BAC} - \widehat {BAD} = {120^o} - {90^o} = {30^o}\)
\(\Delta ADC\) có: \(\widehat C = \widehat {CAD} = {30^o}\) nên \(\Delta ADC\) cân tại \(D\), suy ra \(DC = DA\) (1)
Ta có: \(\widehat {ADB}\) là góc ngoài tại đỉnh \(D\) của \(\Delta ADC\) nên \(\widehat {ADB} = \widehat C + \widehat {CAD} = {30^o} + {30^o} = {60^o}.\)
Trên cạnh \(BD\) lấy \(E\) sao cho \(\widehat {BAE} = {30^o}\) thì \(E\) nằm giữa \(B\) và \(D.\)
\(\Delta AEB\) có: \(\widehat B = \widehat {BAE} = {30^o}\) nên \(\Delta AEB\) cân tại \(E\), suy ra \(AE = EB\) (2)
Ta có: \(\widehat {DAE} = \widehat {BAD} - \widehat {BAE} = {90^o} - {30^o} = {60^o}.\)
\(\Delta ADE\) có: \(\widehat {DAE} = \widehat {ADE} = {60^o}\) nên \(\Delta ADE\) là tam giác đều, suy ra \(DA = DE = AE\) (3)
Từ (1), (2) và (3) suy ra: \(DC = DE = EB = \dfrac{1}{3}BC.\)
Do đó \(BD = DE + EB = \dfrac{2}{3}BC = \dfrac{2}{3}.6 = 4\,\left( {cm} \right).\)
Cho tam giác \(ABC\) vuông tại \(A\) có \(\widehat B = {30^0}.\) Khi đó:
\(AC = \dfrac{{BC}}{2}\)
\(AB = \dfrac{{BC}}{2}\)
\(\Delta ABC\) là tam giác vuông cân
\(AC = \dfrac{{BC}}{3}\)
Đáp án : A
Lấy điểm \(M\) trên cạnh \(BC\) sao cho \(\widehat {BAM} = {30^o}.\) Chứng minh \(\Delta AMB\) cân và \(\Delta AMC\) đều suy ra \(MA = MB = MC = AC\), từ đó suy ra điều phải chứng minh.
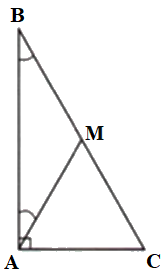
Lấy điểm \(M\) trên cạnh \(BC\) sao cho \(\widehat {BAM} = {30^o}.\)
\(\Delta AMB\) có \(\widehat {BAM} = \widehat B = {30^o}\) nên là tam giác cân, suy ra \(MA = MB\) (1)
\(\Delta ABC\) vuông tại \(A\) nên \(\widehat B + \widehat C = {90^o}\) \( \Rightarrow \widehat C = {90^o} - \widehat B = {90^o} - {30^o} = {60^o}.\)
Ta có: \(\widehat {BAC} = \widehat {BAM} + \widehat {MAC}\)
\( \Rightarrow \widehat {MAC} = \widehat {BAC} - \widehat {BAM} = {90^o} - {30^o} = {60^o}.\)
\(\Delta AMC\) có: \(\widehat {MAC} = \widehat C = {60^o}\) nên là tam giác đều, suy ra \(AC = AM = MC\) (2)
Từ (1) và (2) ta có: \(AC = MB = MC\) hay \(AC = \dfrac{{BC}}{2}.\)
Cho \(M\) thuộc đoạn thẳng \(AB.\) Trên cùng một nửa mặt phẳng bờ \(AB,\) vẽ các tam giác đều \(AMC,BMD.\) Gọi \(E;F\) theo thứ tự là trung điểm của \(AD;BC.\) Tam giác \(MEF\) là tam giác gì? Chọn câu trả lời đúng nhất.
Tam giác nhọn
Tam giác cân
Tam giác đều
Cả A, B, C đều đúng
Đáp án : D
- Sử dụng:
- Tính chất: Tam giác đều có ba cạnh bằng nhau, ba góc bằng nhau và cùng bằng \({60^o}.\)
- Trường hợp bằng nhau thứ hai của tam giác: Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
- Dấu hiệu nhận biết tam giác đều: Tam giác cân có một góc bằng \({60^o}.\)
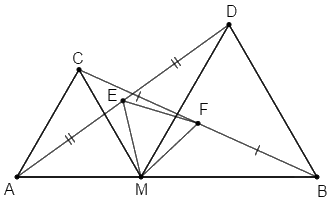
\(\Delta AMC\) đều nên \(\widehat {AMC} = {60^o};\,AM = CM.\)
\(\Delta BMD\) đều nên \(\widehat {BMD} = {60^o};\,MD = MB.\)
\(\widehat {AMD} = \widehat {AMC} + \widehat {CMD} = {60^o} + \widehat {CMD}\) (1)
\(\widehat {CMB} = \widehat {BMD} + \widehat {CMD} = {60^o} + \widehat {CMD}\) (2)
Từ (1) và (2) suy ra: \(\widehat {AMD} = \widehat {CMB}\)
Xét \(\Delta AMD\) và \(\Delta CMB\) có:
\(AM = CM\,\,(cmt)\)
\(\widehat {AMD} = \widehat {CMB}\,\,(cmt)\)
\(MD = MB\,\,(cmt)\)
\( \Rightarrow \Delta AMD = \Delta CMB\,(c.g.c)\)
\( \Rightarrow AD = CB\) (hai cạnh tương ứng).
\( \Rightarrow \widehat {DAM} = \widehat {BCM}\) (hai góc tương ứng).
Xét \(\Delta AEM\) và \(\Delta CFM\) có:
\(AM = CM\,(cmt)\)
\(\widehat {DAM} = \widehat {BCM}\,(cmt)\)
\(AE = CF\,\,\left( {\dfrac{{AD}}{2} = \dfrac{{CB}}{2}} \right)\)
\( \Rightarrow \Delta AEM = \Delta CFM\,(c.g.c)\)
\( \Rightarrow EM = FM\) (hai cạnh tương ứng).
\( \Rightarrow \widehat {AME} = \widehat {CMF}\) (hai góc tương ứng)
\( \Rightarrow \widehat {AMC} + \widehat {CME} = \widehat {CME} + \widehat {EMF}\)
\( \Rightarrow \widehat {AMC} = \widehat {EMF}\)
\( \Rightarrow \widehat {EMF} = {60^o}\)
Xét \(\Delta MEF\) có: \(EM = FM\,(cmt);\,\widehat {EMF} = {60^o}\,(cmt)\) nên \(\Delta MEF\) là tam giác đều.
Tam giác đều vừa là tam giác cân vừa là tam giác nhọn (vì có ba góc nhọn) nên cả A, B, C đều đúng.
Cho tam giác $ABC$ có \(\widehat A = {60^ \circ }\). Vẽ ra phía ngoài của tam giác hai tam giác đều $AMB$ và $ANC.$
Ba điểm $M,A,N$ thẳng hàng.
$BN = CM$
Cả A, B đều sai
Cả A, B đều đúng
Đáp án : D
+ Ta sử dụng tính chất tam giác cân, tính chất tia phân giác của một góc, tính chất hai góc kề bù để chứng minh các cặp góc so le trong bằng nhau để chứng minh ba điểm $M,A,N$ thẳng hàng.
+ Chứng minh cạnh bằng nhau ta sử dụng các trường hợp bằng nhau của tam giác để chứng minh hai tam giác bằng nhau từ đó suy ra hai cạnh tương ứng bằng nhau.
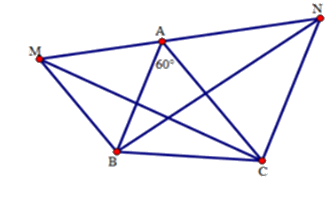
+ Các tam giác $AMB$ và $ANC$ là các tam giác đều(gt) nên \(\widehat {MAB} = {60^0},\,\,\,\widehat {NAC} = {60^0}\).
Ta có: \(\widehat {MAB} + \widehat {BAC} + \widehat {CAN} = {60^0} + {60^0} + {60^0} = {180^0}.\)
Suy ra ba điểm $M,A,N$ thẳng hàng.
+ Ta có:
$\widehat {MAC} = \widehat {MAB} + \widehat {BAC} = {60^0} + {60^0} = {120^0}\\\widehat {BAN} = \widehat {CAN} + \widehat {BAC} = {60^0} + {60^0} = {120^0}$
Do đó \(\widehat {MAC} = \widehat {BAN}\) .
Xét hai tam giác $ABN$ và $AMC$ có:
+) $AB = AM$ (do tam giác $AMB$ đều)
+) \(\widehat {BAN} = \widehat {MAC}\) (cmt)
+) $AN = AC$ (do tam giác $ANC$ đều)
Do đó \(\Delta ABN = \Delta AMC(c.g.c)\)
Suy ra $BN = CM$ (hai cạnh tương ứng).
Vậy cả A, B đều đúng.
Cho tam giác \(ABC\) có \(\widehat A = 120^\circ .\) Trên tia phân giác của góc \(A\) lấy điểm \(D\) sao cho \(AD = AB + AC.\) Khi đó tam giác \(BCD\) là tam giác gì?
cân
đều
vuông
vuông cân
Đáp án : B
Dựa vào tính chất tổng các góc của tam giác và dựa vào tính chất tam giác cân.
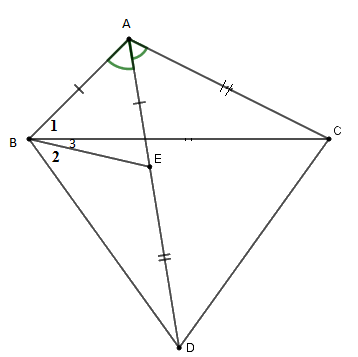
Lấy \(E \in AD\) sao cho \(AE = AB\) mà \(AD = AB + AC\) nên \(AC = DE.\)
\(\Delta ABE\) cân có \(\widehat {BAD} = 60^\circ \) nên \(\Delta ABE\) là tam giác đều suy ra \(AE = EB.\)
Thấy \(\widehat {BED} = \widehat {EBA} + \widehat {EAB} = 120^\circ \) (góc ngoài tại đỉnh \(E\) của tam giác \(ABE\) ) nên \(\widehat {BED} = \widehat {BAC}\left( { = 120^\circ } \right)\)
Suy ra \(\Delta EBD = \Delta {\rm A}BC\left( {c.g.c} \right) \Rightarrow \widehat {{B_1}} = \widehat {{B_2}}\) (hai góc tương ứng bằng nhau) và \(BD = BC\) (hai cạnh tương ứng)
Lại có $\widehat {{B_1}} + \widehat {{B_3}} = 60^\circ $ nên \(\widehat {{B_2}} + \widehat {{B_3}} = 60^\circ .\)
\(\Delta BCD\) cân tại \(B\) có \(\widehat {CBD} = 60^\circ \) nên nó là tam giác đều.
Tam giác \(ABC\) có \(\widehat A = 40^\circ ;\,\widehat B - \widehat C = 20^\circ .\) Trên tia đối của tia \(AC\) lấy điểm \(E\) sao cho \(AE = AB.\) Tính số đo góc \(CBE.\)
\(80^\circ \)
\(100^\circ \)
\(90^\circ \)
\(120^\circ \)
Đáp án : B
Dựa vào tính chất tổng các góc của tam giác và dựa vào tính chất tam giác cân.
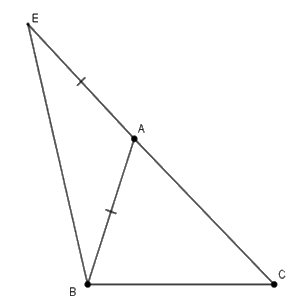
Xét tam giác \(ABC\) có \(\widehat A + \widehat B + \widehat C = 180^\circ \) (định lý tổng ba góc trong tam giác) và \(\widehat A = 40^\circ ;\,\widehat B - \widehat C = 20^\circ \,\left( {gt} \right)\)
Suy ra \(\widehat B + \widehat C = 140^\circ \) nên \(\widehat B = \dfrac{{140^\circ + 20^\circ }}{2} = 80^\circ ;\,\widehat C = 60^\circ \)
Xét tam giác \(AEB\) cân tại \(A\) (do \(AB = AE\,\left( {gt} \right)\)) nên \(\widehat {AEB} = \widehat {ABE}\) (tính chất) (1)
Lại có \(\widehat {BAC}\) là góc ngoài của tam giác \(AEB \Rightarrow \widehat {BAC} = \widehat {AEB} + \widehat {ABE}\) (2)
Từ (1) và (2) suy ra \(\widehat {ABE} = \dfrac{{\widehat {BAC}}}{2} = 20^\circ \)
Do đó \(\widehat {CBE} = \widehat {CBA} + \widehat {ABE} = 80^\circ + 20^\circ = 100^\circ .\)
Cho tam giác \(ABC\) có \(M\) là trung điểm của \(BC\) và \(AM = \dfrac{{BC}}{2}\). Số đo góc \(BAC\) là
\(45^\circ \)
\(30^0\)
\(90^\circ \)
\(60^\circ \)
Đáp án : C
Dựa vào tính chất tổng các góc của tam giác và dựa vào tính chất tam giác cân.
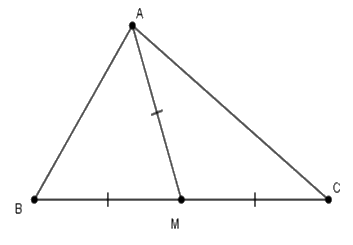
Từ giả thiết suy ra \(AM = BM = CM\)
Ta có \(\widehat {BAC} + \widehat B + \widehat C = 180^\circ \) (định lý tổng ba góc trong tam giác) (1)
Lại có \(\Delta AMB\) cân tại \(M\,\left( {{\rm{do}}\,\,MA = MB} \right)\) nên \(\widehat B = \widehat {BAM}\) (tính chất) (2)
Tương tự \(\Delta AMC\) cân tại \(M\,\left( {{\mathop{\rm do}\nolimits} \,\,MA = MC} \right)\) nên \(\widehat C = \widehat {MAC}\) (tính chất) (3)
Từ (1); (2); (3) ta có \(\widehat {BAC} + \widehat {BAM} + \widehat {CAM} = 180^\circ \) \( \Rightarrow \widehat {BAC} + \widehat {BAC} = 180^\circ \) \(2.\widehat {BAC} = 180^\circ \) \( \Rightarrow \widehat {BAC} = 90^\circ .\)
Cho tam giác \(ABC\) có \(\widehat A = 90^\circ ;\,AB = AC\). Khi đó
\(\Delta ABC\) là tam giác vuông
\(\Delta ABC\) là tam giác cân
\(\Delta ABC\) là tam giác vuông cân
Cả A, B, C đều đúng.
Đáp án : D
Tam giác \(ABC\) có \(\widehat A = 90^\circ ;\,AB = AC\) nên tam giác \(ABC\) vuông cân.
Tam giác vuông cân là tam giác vừa vuông vừa cân nên cả A, B, C đều đúng.
Cho tam giác $ABC$ cân tại đỉnh $A$ với \(\widehat A = {80^0}\). Trên hai cạnh $AB,AC$ lần lượt lấy hai điểm $D$ và $E$ sao cho $AD = AE.$ Phát biểu nào sau đây là sai?
$DE//BC$
\(\widehat B = {50^0}\)
\(\widehat {ADE} = {50^0}\)
Cả ba phát biểu trên đều sai
Đáp án : D
Sử dụng tính chất tam giác cân, tính chất tổng các góc của một tam giác, dấu hiệu nhận biết hai đường thẳng song song.
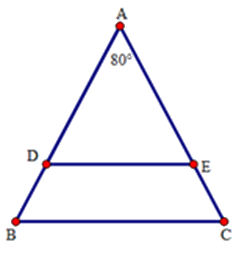
Do tam giác ABC cân nên \(\widehat B = \dfrac{{{{180}^0} - \widehat A}}{2} = \dfrac{{{{180}^0} - {{80}^0}}}{2} = {50^0}\)
Ta thấy tam giác $ADE$ cân do $AD = AE.$
\( \Rightarrow \widehat {ADE} = \dfrac{{{{180}^0} - \widehat A}}{2} = \dfrac{{{{180}^0} - {{80}^0}}}{2} = {50^0}\)
Do đó \(\widehat B = \widehat {ADE}\) . Mà hai góc này ở vị trí so le trong nên $ED//BC.$
Vậy D là đáp án sai.
Cho tam giác $ABC$ vuông cân ở $A.$ Trên đáy $BC$ lấy hai điểm $M,N$ sao cho $BM = CN = AB.$
Tam giác \(AMN\) là tam giác gì?
cân
vuông cân
đều
vuông
Đáp án: A
Để chứng minh tam giác $AMN$ cân, ta chứng minh hai góc ở đáy bằng nhau \(\widehat {AMN} = \widehat {ANM}\).
Do tam giác $ABC$ vuông cân ở $A$ nên \(\widehat B = \widehat C = {45^0}\).
Xét tam giác $AMB$ có: $BM = BA(gt),$ nên tam giác $AMB$ cân ở $B.$
Do đó $\widehat {AMB} = \dfrac{{{{180}^0} - \widehat B}}{2}$$ = \dfrac{{{{180}^0} - {{45}^0}}}{2} = {67^0}30'$
Chứng minh tương tự ta được tam giác $ANC$ cân ở $C$ và \(\widehat {ANC} = {67^0}30'\).
Xét tam giác $AMN$ có: \(\widehat {AMN} = \widehat {ANM} = {67^0}30'\), do đó tam giác $AMN$ cân ở $A.$
Tính số đo góc \(\widehat {MAN.}\)
\(45^\circ \)
\(30^\circ \)
\(90^\circ \)
\(60^\circ \)
Đáp án: A
Dựa vào tính chất tổng các góc của tam giác và dựa vào tính chất tam giác cân.
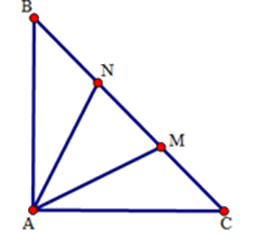
Xét tam giác $AMN,$ ta có:
\(\widehat {MAN} = {180^0} - \left( {\widehat {AMN} + \widehat {ANM}} \right) \)\(= {180^0} - {135^0} = {45^0}.\)
Vậy \(\widehat {MAN} = {45^0}.\)
Tính số đo \(x\) trên hình vẽ sau:
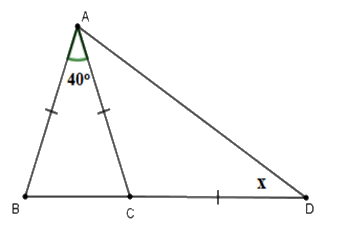
\(x = 45^\circ .\)
\(x = 40^\circ .\)
\(x = 35^\circ .\)
\(x = 70^\circ .\)
Đáp án : C
Sử dụng tính chất tổng ba góc của một tam giác, tính chất góc ngoài và sử dụng tính chất của tam giác cân.
Tam giác \(ABC\) cân tại \(A\) (vì \(AB = AC\) ) có \(\widehat A = 40^\circ \) nên \(\widehat B = \widehat {ACB} = \dfrac{{180^\circ - 40^\circ }}{2} = 70^\circ \)
Mà \(\widehat {ACB}\) là góc ngoài của tam giác \(ACD\) nên \(\widehat {ACB} = \widehat {CAD} + \widehat {CDA}\)
Lại có \(\Delta CAD\) cân tại \(C \Rightarrow \widehat {CAD} = \widehat {CDA} = x\) (tính chất)
Nên \(\widehat {ACB} = \widehat {CAD} + \widehat {CDA} = 2x \Rightarrow x = \dfrac{{\widehat {ACB}}}{2}\)\( = \dfrac{{70^\circ }}{2} = 35^\circ .\)
Vậy \(x = 35^\circ .\)
Số tam giác cân trong hình vẽ dưới đây là:
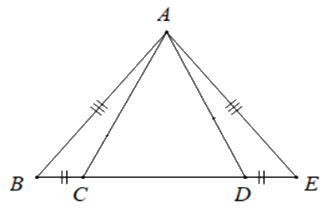
\(2\)
\(1\)
\(3\)
\(4\)
Đáp án : A
Từ hình vẽ ta có \(AB = AE;BC = DE\)
Vì \(AB = AE \Rightarrow \Delta ABE\) cân tại \(A.\)
Suy ra \(\widehat B = \widehat E\) (hai góc ở đáy)
Xét tam giác \(ABC\) và \(AED\) có: \(AB = AE;\widehat B = \widehat E\left( {cmt} \right);BC = DE\) nên \(\Delta ABC = \Delta AED\left( {c - g - c} \right)\)
Do đó \(AC = AD\) (hai cạnh tương ứng) suy ra \(\Delta ACD\) cân tại \(A.\)
Vậy có hai tam giác cân trên hình vẽ.
Một tam giác cân có góc ở đáy bằng \({70^0}\) thì số đo góc ở đỉnh là:
\({54^0}\)
\({63^0}\)
\({70^0}\)
\({40^0}\)
Đáp án : D
Sử dụng tính chất tổng ba góc của một tam giác và sử dụng tính chất của tam giác cân.
Tổng số đo hai góc ở đáy là \(70^o.2 = 140^\circ \)
Vì tổng ba góc của tam giác bằng \(180^\circ \) nên số đo góc ở đỉnh tam giác cân này là
\(180^\circ - 140^\circ = 40^\circ .\)
Một tam giác cân có góc ở đỉnh bằng \({64^0}\) thì số đo góc ở đáy là:
\({54^0}\)
\({58^0}\)
\({72^0}\)
\({90^0}\)
Đáp án : B
Sử dụng tính chất tổng ba góc của một tam giác và sử dụng tính chất của tam giác cân.
Sử dụng cách tính số đo các góc trong tam giác $ABC$ cân tại $A.$
Góc ở đỉnh \(\widehat A = {180^0} - 2\widehat C\) và góc ở đáy \(\widehat C = \dfrac{{{{180}^0} - \widehat A}}{2}.\)
Áp dụng ta có số đo góc ở đáy bằng: $\dfrac{{{{180}^0} - {{64}^0}}}{2} = {58^0}$
Cho tam giác $ABC$ cân tại $A.$ Phát biểu nào trong các phát biểu sau là sai:
\(\widehat B = \widehat C\)
\(\widehat C = \dfrac{{{{180}^0} - \widehat A}}{2}\)
\(\widehat A = {180^0} - 2\widehat C\)
\(\widehat B \ne \widehat C\)
Đáp án : D
+ Áp dụng tính chất của tam giác cân và tính chất tổng các góc của một tam giác
Do tam giác ABC cân nên \(\widehat B = \widehat C\)
Xét tam giác ABC ta có: \(\widehat A + \widehat B + \widehat C = {180^0} \Leftrightarrow \widehat B + \widehat C = {180^0} - \widehat A \Leftrightarrow \widehat C = \dfrac{{{{180}^0} - \widehat A}}{2}\) hay \(\widehat A = {180^0} - 2\widehat C\)
Hai góc nhọn của tam giác vuông cân bằng nhau và bằng
\(30^\circ \)
\(45^\circ \)
\(60^\circ \)
\(90^\circ \)
Đáp án : B
Mỗi góc nhọn của tam giác vuông cân bằng \({45^0}.\)
Chọn câu sai.
Tam giác đều có ba góc bằng nhau và bằng \(60^\circ .\)
Tam giác đều có ba cạnh bằng nhau.
Tam giác cân là tam giác đều.
Tam giác đều là tam giác cân.
Đáp án : C
Tam giác đều là tam giác có ba cạnh bằng nhau.
Trong tam giác đều, mỗi góc bằng \({60^0}.\)
Nên A, B đúng.
Tam giác đều cũng là tam giác cân nhưng tam giác cân chưa chắc là tam giác đều vì nó chỉ có hai cạnh bên bằng nhau.
Vậy C sai.
Cho tam giác \(ABC\) cân tại \(A\) có: \(\widehat A = {100^0}, BC = a, AC = b.\) Về phía ngoài tam giác \(ABC\) vẽ tam giác \(ABD\) cân tại \(D\) có: \(\widehat {ADB} = {140^0}.\) Tính chu vi tam giác \(ABD\) theo \(a\) và \(b.\)
\(2a + b\)
\(a - b\)
\(2a - b\)
\(2a - 2b\)
Cho tam giác \(ABC\) cân tại \(A\) có \(\widehat A = {120^0},BC = 6cm.\) Đường vuông góc với \(AB\) tại \(A\) cắt \(BC\) ở \(D.\) Độ dài \(BD\) bằng:
\(2\,cm\)
\(3\,cm\)
\(4\,cm\)
\(5\,cm\)
Cho tam giác \(ABC\) vuông tại \(A\) có \(\widehat B = {30^0}.\) Khi đó:
\(AC = \dfrac{{BC}}{2}\)
\(AB = \dfrac{{BC}}{2}\)
\(\Delta ABC\) là tam giác vuông cân
\(AC = \dfrac{{BC}}{3}\)
Cho \(M\) thuộc đoạn thẳng \(AB.\) Trên cùng một nửa mặt phẳng bờ \(AB,\) vẽ các tam giác đều \(AMC,BMD.\) Gọi \(E;F\) theo thứ tự là trung điểm của \(AD;BC.\) Tam giác \(MEF\) là tam giác gì? Chọn câu trả lời đúng nhất.
Tam giác nhọn
Tam giác cân
Tam giác đều
Cả A, B, C đều đúng
Cho tam giác $ABC$ có \(\widehat A = {60^ \circ }\). Vẽ ra phía ngoài của tam giác hai tam giác đều $AMB$ và $ANC.$
Ba điểm $M,A,N$ thẳng hàng.
$BN = CM$
Cả A, B đều sai
Cả A, B đều đúng
Cho tam giác \(ABC\) có \(\widehat A = 120^\circ .\) Trên tia phân giác của góc \(A\) lấy điểm \(D\) sao cho \(AD = AB + AC.\) Khi đó tam giác \(BCD\) là tam giác gì?
cân
đều
vuông
vuông cân
Tam giác \(ABC\) có \(\widehat A = 40^\circ ;\,\widehat B - \widehat C = 20^\circ .\) Trên tia đối của tia \(AC\) lấy điểm \(E\) sao cho \(AE = AB.\) Tính số đo góc \(CBE.\)
\(80^\circ \)
\(100^\circ \)
\(90^\circ \)
\(120^\circ \)
Cho tam giác \(ABC\) có \(M\) là trung điểm của \(BC\) và \(AM = \dfrac{{BC}}{2}\). Số đo góc \(BAC\) là
\(45^\circ \)
\(30^0\)
\(90^\circ \)
\(60^\circ \)
Cho tam giác \(ABC\) có \(\widehat A = 90^\circ ;\,AB = AC\). Khi đó
\(\Delta ABC\) là tam giác vuông
\(\Delta ABC\) là tam giác cân
\(\Delta ABC\) là tam giác vuông cân
Cả A, B, C đều đúng.
Cho tam giác $ABC$ cân tại đỉnh $A$ với \(\widehat A = {80^0}\). Trên hai cạnh $AB,AC$ lần lượt lấy hai điểm $D$ và $E$ sao cho $AD = AE.$ Phát biểu nào sau đây là sai?
$DE//BC$
\(\widehat B = {50^0}\)
\(\widehat {ADE} = {50^0}\)
Cả ba phát biểu trên đều sai
Cho tam giác $ABC$ vuông cân ở $A.$ Trên đáy $BC$ lấy hai điểm $M,N$ sao cho $BM = CN = AB.$
Tam giác \(AMN\) là tam giác gì?
cân
vuông cân
đều
vuông
Tính số đo góc \(\widehat {MAN.}\)
\(45^\circ \)
\(30^\circ \)
\(90^\circ \)
\(60^\circ \)
Tính số đo \(x\) trên hình vẽ sau:

\(x = 45^\circ .\)
\(x = 40^\circ .\)
\(x = 35^\circ .\)
\(x = 70^\circ .\)
Số tam giác cân trong hình vẽ dưới đây là:

\(2\)
\(1\)
\(3\)
\(4\)
Một tam giác cân có góc ở đáy bằng \({70^0}\) thì số đo góc ở đỉnh là:
\({54^0}\)
\({63^0}\)
\({70^0}\)
\({40^0}\)
Một tam giác cân có góc ở đỉnh bằng \({64^0}\) thì số đo góc ở đáy là:
\({54^0}\)
\({58^0}\)
\({72^0}\)
\({90^0}\)
Cho tam giác $ABC$ cân tại $A.$ Phát biểu nào trong các phát biểu sau là sai:
\(\widehat B = \widehat C\)
\(\widehat C = \dfrac{{{{180}^0} - \widehat A}}{2}\)
\(\widehat A = {180^0} - 2\widehat C\)
\(\widehat B \ne \widehat C\)
Hai góc nhọn của tam giác vuông cân bằng nhau và bằng
\(30^\circ \)
\(45^\circ \)
\(60^\circ \)
\(90^\circ \)
Chọn câu sai.
Tam giác đều có ba góc bằng nhau và bằng \(60^\circ .\)
Tam giác đều có ba cạnh bằng nhau.
Tam giác cân là tam giác đều.
Tam giác đều là tam giác cân.
Cho tam giác \(ABC\) cân tại \(A\) có: \(\widehat A = {100^0}, BC = a, AC = b.\) Về phía ngoài tam giác \(ABC\) vẽ tam giác \(ABD\) cân tại \(D\) có: \(\widehat {ADB} = {140^0}.\) Tính chu vi tam giác \(ABD\) theo \(a\) và \(b.\)
\(2a + b\)
\(a - b\)
\(2a - b\)
\(2a - 2b\)
Đáp án : C
- Trên cạnh \(BC\) lấy điểm \(E\) sao cho \(BE = BD.\)
- Chứng minh \(\Delta BDE\) đều, suy ra \(BD = BE = DE = DA.\)
- Chứng minh \(\Delta CAE\) cân tại \(C\), suy ra \(AC = EC.\)
- Biểu diễn \(AD;\,BD;\,AB\) theo \(a,\,b.\) Từ đó tính chu vi của \(\Delta ABD\).

Trên cạnh \(BC\) lấy điểm \(E\) sao cho \(BE = BD.\)
\(\Delta ABC\) cân tại \(A\) nên \(\widehat {ABC} = \dfrac{{{{180}^o} - \widehat {BAC}}}{2} = \dfrac{{{{180}^o} - {{100}^o}}}{2} = {40^o}.\)
\(\Delta ABD\) cân tại \(D\) nên \(\widehat {DBA} = \dfrac{{{{180}^o} - \widehat {ADB}}}{2} = \dfrac{{{{180}^o} - {{140}^o}}}{2} = {20^o}\).
Ta có: \(\widehat {DBE} = \widehat {DBA} + \widehat {ABC} = {20^o} + {40^o} = {60^o}.\)
Xét \(\Delta BDE\) có: \(\widehat {DBE} = {60^o}\) nên \(\Delta BDE\) đều, suy ra \(BD = BE = DE = DA.\)
\(\widehat {EDA} = \widehat {BDA} - \widehat {BDE} = {140^o} - {60^o} = {80^o}\)
\(\Delta DAE\) cân tại \(D\) (vì \(DA = DE\,(cmt)\)) nên \(\widehat {DEA} = \widehat {DAE} = \dfrac{{{{180}^o} - \widehat {EDA}}}{2} = \dfrac{{{{180}^o} - {{80}^o}}}{2} = {50^o}.\)
\(\widehat {EAC} = \widehat {DAB} + \widehat {BAC} - \widehat {DAE} = {20^o} + {100^o} - {50^o} = {70^o}.\)
\(\widehat {AEC} = {180^o} - \widehat {DEA} - \widehat {DEB} = {180^o} - {50^o} - {60^o} = {70^o}.\)
\(\Delta CAE\) có \(\widehat {EAC} = \widehat {AEC} = {70^o}\) nên \(\Delta CAE\) cân tại \(C\), suy ra \(AC = EC.\)
Do đó: \(AD = BD = BE = BC - EC = BC - AC = a - b.\)
\(AB = AC = b.\)
Vậy chu vi của \(\Delta ABD\) là:
\(AD + BD + AB = a - b + a - b + b = 2a - b.\)
Cho tam giác \(ABC\) cân tại \(A\) có \(\widehat A = {120^0},BC = 6cm.\) Đường vuông góc với \(AB\) tại \(A\) cắt \(BC\) ở \(D.\) Độ dài \(BD\) bằng:
\(2\,cm\)
\(3\,cm\)
\(4\,cm\)
\(5\,cm\)
Đáp án : C
- Chứng minh \(\Delta ADC\) cân tại \(D\), suy ra \(DC = DA\) (1)
- Trên cạnh \(BD\) lấy \(E\) sao cho \(\widehat {BAE} = {30^o}\), chứng minh \(\Delta AEB\) cân tại \(E\), suy ra \(AE = EB\) (2)
- Chứng minh \(\Delta ADE\) là tam giác đều, suy ra \(DA = DE = AE\) (3)
- Từ (1), (2) và (3) suy ra: \(DC = DE = EB = \dfrac{1}{3}BC\), từ đó ta tính được độ dài \(BD.\)

\(\Delta ABC\) cân tại \(\widehat A\) nên \(\widehat B = \widehat C = \dfrac{{{{180}^o} - \widehat A}}{2} = \dfrac{{{{180}^o} - {{120}^o}}}{2} = {30^o}.\)
Ta có: \(\widehat {CAD} = \widehat {BAC} - \widehat {BAD} = {120^o} - {90^o} = {30^o}\)
\(\Delta ADC\) có: \(\widehat C = \widehat {CAD} = {30^o}\) nên \(\Delta ADC\) cân tại \(D\), suy ra \(DC = DA\) (1)
Ta có: \(\widehat {ADB}\) là góc ngoài tại đỉnh \(D\) của \(\Delta ADC\) nên \(\widehat {ADB} = \widehat C + \widehat {CAD} = {30^o} + {30^o} = {60^o}.\)
Trên cạnh \(BD\) lấy \(E\) sao cho \(\widehat {BAE} = {30^o}\) thì \(E\) nằm giữa \(B\) và \(D.\)
\(\Delta AEB\) có: \(\widehat B = \widehat {BAE} = {30^o}\) nên \(\Delta AEB\) cân tại \(E\), suy ra \(AE = EB\) (2)
Ta có: \(\widehat {DAE} = \widehat {BAD} - \widehat {BAE} = {90^o} - {30^o} = {60^o}.\)
\(\Delta ADE\) có: \(\widehat {DAE} = \widehat {ADE} = {60^o}\) nên \(\Delta ADE\) là tam giác đều, suy ra \(DA = DE = AE\) (3)
Từ (1), (2) và (3) suy ra: \(DC = DE = EB = \dfrac{1}{3}BC.\)
Do đó \(BD = DE + EB = \dfrac{2}{3}BC = \dfrac{2}{3}.6 = 4\,\left( {cm} \right).\)
Cho tam giác \(ABC\) vuông tại \(A\) có \(\widehat B = {30^0}.\) Khi đó:
\(AC = \dfrac{{BC}}{2}\)
\(AB = \dfrac{{BC}}{2}\)
\(\Delta ABC\) là tam giác vuông cân
\(AC = \dfrac{{BC}}{3}\)
Đáp án : A
Lấy điểm \(M\) trên cạnh \(BC\) sao cho \(\widehat {BAM} = {30^o}.\) Chứng minh \(\Delta AMB\) cân và \(\Delta AMC\) đều suy ra \(MA = MB = MC = AC\), từ đó suy ra điều phải chứng minh.

Lấy điểm \(M\) trên cạnh \(BC\) sao cho \(\widehat {BAM} = {30^o}.\)
\(\Delta AMB\) có \(\widehat {BAM} = \widehat B = {30^o}\) nên là tam giác cân, suy ra \(MA = MB\) (1)
\(\Delta ABC\) vuông tại \(A\) nên \(\widehat B + \widehat C = {90^o}\) \( \Rightarrow \widehat C = {90^o} - \widehat B = {90^o} - {30^o} = {60^o}.\)
Ta có: \(\widehat {BAC} = \widehat {BAM} + \widehat {MAC}\)
\( \Rightarrow \widehat {MAC} = \widehat {BAC} - \widehat {BAM} = {90^o} - {30^o} = {60^o}.\)
\(\Delta AMC\) có: \(\widehat {MAC} = \widehat C = {60^o}\) nên là tam giác đều, suy ra \(AC = AM = MC\) (2)
Từ (1) và (2) ta có: \(AC = MB = MC\) hay \(AC = \dfrac{{BC}}{2}.\)
Cho \(M\) thuộc đoạn thẳng \(AB.\) Trên cùng một nửa mặt phẳng bờ \(AB,\) vẽ các tam giác đều \(AMC,BMD.\) Gọi \(E;F\) theo thứ tự là trung điểm của \(AD;BC.\) Tam giác \(MEF\) là tam giác gì? Chọn câu trả lời đúng nhất.
Tam giác nhọn
Tam giác cân
Tam giác đều
Cả A, B, C đều đúng
Đáp án : D
- Sử dụng:
- Tính chất: Tam giác đều có ba cạnh bằng nhau, ba góc bằng nhau và cùng bằng \({60^o}.\)
- Trường hợp bằng nhau thứ hai của tam giác: Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
- Dấu hiệu nhận biết tam giác đều: Tam giác cân có một góc bằng \({60^o}.\)

\(\Delta AMC\) đều nên \(\widehat {AMC} = {60^o};\,AM = CM.\)
\(\Delta BMD\) đều nên \(\widehat {BMD} = {60^o};\,MD = MB.\)
\(\widehat {AMD} = \widehat {AMC} + \widehat {CMD} = {60^o} + \widehat {CMD}\) (1)
\(\widehat {CMB} = \widehat {BMD} + \widehat {CMD} = {60^o} + \widehat {CMD}\) (2)
Từ (1) và (2) suy ra: \(\widehat {AMD} = \widehat {CMB}\)
Xét \(\Delta AMD\) và \(\Delta CMB\) có:
\(AM = CM\,\,(cmt)\)
\(\widehat {AMD} = \widehat {CMB}\,\,(cmt)\)
\(MD = MB\,\,(cmt)\)
\( \Rightarrow \Delta AMD = \Delta CMB\,(c.g.c)\)
\( \Rightarrow AD = CB\) (hai cạnh tương ứng).
\( \Rightarrow \widehat {DAM} = \widehat {BCM}\) (hai góc tương ứng).
Xét \(\Delta AEM\) và \(\Delta CFM\) có:
\(AM = CM\,(cmt)\)
\(\widehat {DAM} = \widehat {BCM}\,(cmt)\)
\(AE = CF\,\,\left( {\dfrac{{AD}}{2} = \dfrac{{CB}}{2}} \right)\)
\( \Rightarrow \Delta AEM = \Delta CFM\,(c.g.c)\)
\( \Rightarrow EM = FM\) (hai cạnh tương ứng).
\( \Rightarrow \widehat {AME} = \widehat {CMF}\) (hai góc tương ứng)
\( \Rightarrow \widehat {AMC} + \widehat {CME} = \widehat {CME} + \widehat {EMF}\)
\( \Rightarrow \widehat {AMC} = \widehat {EMF}\)
\( \Rightarrow \widehat {EMF} = {60^o}\)
Xét \(\Delta MEF\) có: \(EM = FM\,(cmt);\,\widehat {EMF} = {60^o}\,(cmt)\) nên \(\Delta MEF\) là tam giác đều.
Tam giác đều vừa là tam giác cân vừa là tam giác nhọn (vì có ba góc nhọn) nên cả A, B, C đều đúng.
Cho tam giác $ABC$ có \(\widehat A = {60^ \circ }\). Vẽ ra phía ngoài của tam giác hai tam giác đều $AMB$ và $ANC.$
Ba điểm $M,A,N$ thẳng hàng.
$BN = CM$
Cả A, B đều sai
Cả A, B đều đúng
Đáp án : D
+ Ta sử dụng tính chất tam giác cân, tính chất tia phân giác của một góc, tính chất hai góc kề bù để chứng minh các cặp góc so le trong bằng nhau để chứng minh ba điểm $M,A,N$ thẳng hàng.
+ Chứng minh cạnh bằng nhau ta sử dụng các trường hợp bằng nhau của tam giác để chứng minh hai tam giác bằng nhau từ đó suy ra hai cạnh tương ứng bằng nhau.

+ Các tam giác $AMB$ và $ANC$ là các tam giác đều(gt) nên \(\widehat {MAB} = {60^0},\,\,\,\widehat {NAC} = {60^0}\).
Ta có: \(\widehat {MAB} + \widehat {BAC} + \widehat {CAN} = {60^0} + {60^0} + {60^0} = {180^0}.\)
Suy ra ba điểm $M,A,N$ thẳng hàng.
+ Ta có:
$\widehat {MAC} = \widehat {MAB} + \widehat {BAC} = {60^0} + {60^0} = {120^0}\\\widehat {BAN} = \widehat {CAN} + \widehat {BAC} = {60^0} + {60^0} = {120^0}$
Do đó \(\widehat {MAC} = \widehat {BAN}\) .
Xét hai tam giác $ABN$ và $AMC$ có:
+) $AB = AM$ (do tam giác $AMB$ đều)
+) \(\widehat {BAN} = \widehat {MAC}\) (cmt)
+) $AN = AC$ (do tam giác $ANC$ đều)
Do đó \(\Delta ABN = \Delta AMC(c.g.c)\)
Suy ra $BN = CM$ (hai cạnh tương ứng).
Vậy cả A, B đều đúng.
Cho tam giác \(ABC\) có \(\widehat A = 120^\circ .\) Trên tia phân giác của góc \(A\) lấy điểm \(D\) sao cho \(AD = AB + AC.\) Khi đó tam giác \(BCD\) là tam giác gì?
cân
đều
vuông
vuông cân
Đáp án : B
Dựa vào tính chất tổng các góc của tam giác và dựa vào tính chất tam giác cân.

Lấy \(E \in AD\) sao cho \(AE = AB\) mà \(AD = AB + AC\) nên \(AC = DE.\)
\(\Delta ABE\) cân có \(\widehat {BAD} = 60^\circ \) nên \(\Delta ABE\) là tam giác đều suy ra \(AE = EB.\)
Thấy \(\widehat {BED} = \widehat {EBA} + \widehat {EAB} = 120^\circ \) (góc ngoài tại đỉnh \(E\) của tam giác \(ABE\) ) nên \(\widehat {BED} = \widehat {BAC}\left( { = 120^\circ } \right)\)
Suy ra \(\Delta EBD = \Delta {\rm A}BC\left( {c.g.c} \right) \Rightarrow \widehat {{B_1}} = \widehat {{B_2}}\) (hai góc tương ứng bằng nhau) và \(BD = BC\) (hai cạnh tương ứng)
Lại có $\widehat {{B_1}} + \widehat {{B_3}} = 60^\circ $ nên \(\widehat {{B_2}} + \widehat {{B_3}} = 60^\circ .\)
\(\Delta BCD\) cân tại \(B\) có \(\widehat {CBD} = 60^\circ \) nên nó là tam giác đều.
Tam giác \(ABC\) có \(\widehat A = 40^\circ ;\,\widehat B - \widehat C = 20^\circ .\) Trên tia đối của tia \(AC\) lấy điểm \(E\) sao cho \(AE = AB.\) Tính số đo góc \(CBE.\)
\(80^\circ \)
\(100^\circ \)
\(90^\circ \)
\(120^\circ \)
Đáp án : B
Dựa vào tính chất tổng các góc của tam giác và dựa vào tính chất tam giác cân.

Xét tam giác \(ABC\) có \(\widehat A + \widehat B + \widehat C = 180^\circ \) (định lý tổng ba góc trong tam giác) và \(\widehat A = 40^\circ ;\,\widehat B - \widehat C = 20^\circ \,\left( {gt} \right)\)
Suy ra \(\widehat B + \widehat C = 140^\circ \) nên \(\widehat B = \dfrac{{140^\circ + 20^\circ }}{2} = 80^\circ ;\,\widehat C = 60^\circ \)
Xét tam giác \(AEB\) cân tại \(A\) (do \(AB = AE\,\left( {gt} \right)\)) nên \(\widehat {AEB} = \widehat {ABE}\) (tính chất) (1)
Lại có \(\widehat {BAC}\) là góc ngoài của tam giác \(AEB \Rightarrow \widehat {BAC} = \widehat {AEB} + \widehat {ABE}\) (2)
Từ (1) và (2) suy ra \(\widehat {ABE} = \dfrac{{\widehat {BAC}}}{2} = 20^\circ \)
Do đó \(\widehat {CBE} = \widehat {CBA} + \widehat {ABE} = 80^\circ + 20^\circ = 100^\circ .\)
Cho tam giác \(ABC\) có \(M\) là trung điểm của \(BC\) và \(AM = \dfrac{{BC}}{2}\). Số đo góc \(BAC\) là
\(45^\circ \)
\(30^0\)
\(90^\circ \)
\(60^\circ \)
Đáp án : C
Dựa vào tính chất tổng các góc của tam giác và dựa vào tính chất tam giác cân.

Từ giả thiết suy ra \(AM = BM = CM\)
Ta có \(\widehat {BAC} + \widehat B + \widehat C = 180^\circ \) (định lý tổng ba góc trong tam giác) (1)
Lại có \(\Delta AMB\) cân tại \(M\,\left( {{\rm{do}}\,\,MA = MB} \right)\) nên \(\widehat B = \widehat {BAM}\) (tính chất) (2)
Tương tự \(\Delta AMC\) cân tại \(M\,\left( {{\mathop{\rm do}\nolimits} \,\,MA = MC} \right)\) nên \(\widehat C = \widehat {MAC}\) (tính chất) (3)
Từ (1); (2); (3) ta có \(\widehat {BAC} + \widehat {BAM} + \widehat {CAM} = 180^\circ \) \( \Rightarrow \widehat {BAC} + \widehat {BAC} = 180^\circ \) \(2.\widehat {BAC} = 180^\circ \) \( \Rightarrow \widehat {BAC} = 90^\circ .\)
Cho tam giác \(ABC\) có \(\widehat A = 90^\circ ;\,AB = AC\). Khi đó
\(\Delta ABC\) là tam giác vuông
\(\Delta ABC\) là tam giác cân
\(\Delta ABC\) là tam giác vuông cân
Cả A, B, C đều đúng.
Đáp án : D
Tam giác \(ABC\) có \(\widehat A = 90^\circ ;\,AB = AC\) nên tam giác \(ABC\) vuông cân.
Tam giác vuông cân là tam giác vừa vuông vừa cân nên cả A, B, C đều đúng.
Cho tam giác $ABC$ cân tại đỉnh $A$ với \(\widehat A = {80^0}\). Trên hai cạnh $AB,AC$ lần lượt lấy hai điểm $D$ và $E$ sao cho $AD = AE.$ Phát biểu nào sau đây là sai?
$DE//BC$
\(\widehat B = {50^0}\)
\(\widehat {ADE} = {50^0}\)
Cả ba phát biểu trên đều sai
Đáp án : D
Sử dụng tính chất tam giác cân, tính chất tổng các góc của một tam giác, dấu hiệu nhận biết hai đường thẳng song song.

Do tam giác ABC cân nên \(\widehat B = \dfrac{{{{180}^0} - \widehat A}}{2} = \dfrac{{{{180}^0} - {{80}^0}}}{2} = {50^0}\)
Ta thấy tam giác $ADE$ cân do $AD = AE.$
\( \Rightarrow \widehat {ADE} = \dfrac{{{{180}^0} - \widehat A}}{2} = \dfrac{{{{180}^0} - {{80}^0}}}{2} = {50^0}\)
Do đó \(\widehat B = \widehat {ADE}\) . Mà hai góc này ở vị trí so le trong nên $ED//BC.$
Vậy D là đáp án sai.
Cho tam giác $ABC$ vuông cân ở $A.$ Trên đáy $BC$ lấy hai điểm $M,N$ sao cho $BM = CN = AB.$
Tam giác \(AMN\) là tam giác gì?
cân
vuông cân
đều
vuông
Đáp án: A
Để chứng minh tam giác $AMN$ cân, ta chứng minh hai góc ở đáy bằng nhau \(\widehat {AMN} = \widehat {ANM}\).
Do tam giác $ABC$ vuông cân ở $A$ nên \(\widehat B = \widehat C = {45^0}\).
Xét tam giác $AMB$ có: $BM = BA(gt),$ nên tam giác $AMB$ cân ở $B.$
Do đó $\widehat {AMB} = \dfrac{{{{180}^0} - \widehat B}}{2}$$ = \dfrac{{{{180}^0} - {{45}^0}}}{2} = {67^0}30'$
Chứng minh tương tự ta được tam giác $ANC$ cân ở $C$ và \(\widehat {ANC} = {67^0}30'\).
Xét tam giác $AMN$ có: \(\widehat {AMN} = \widehat {ANM} = {67^0}30'\), do đó tam giác $AMN$ cân ở $A.$
Tính số đo góc \(\widehat {MAN.}\)
\(45^\circ \)
\(30^\circ \)
\(90^\circ \)
\(60^\circ \)
Đáp án: A
Dựa vào tính chất tổng các góc của tam giác và dựa vào tính chất tam giác cân.

Xét tam giác $AMN,$ ta có:
\(\widehat {MAN} = {180^0} - \left( {\widehat {AMN} + \widehat {ANM}} \right) \)\(= {180^0} - {135^0} = {45^0}.\)
Vậy \(\widehat {MAN} = {45^0}.\)
Tính số đo \(x\) trên hình vẽ sau:

\(x = 45^\circ .\)
\(x = 40^\circ .\)
\(x = 35^\circ .\)
\(x = 70^\circ .\)
Đáp án : C
Sử dụng tính chất tổng ba góc của một tam giác, tính chất góc ngoài và sử dụng tính chất của tam giác cân.
Tam giác \(ABC\) cân tại \(A\) (vì \(AB = AC\) ) có \(\widehat A = 40^\circ \) nên \(\widehat B = \widehat {ACB} = \dfrac{{180^\circ - 40^\circ }}{2} = 70^\circ \)
Mà \(\widehat {ACB}\) là góc ngoài của tam giác \(ACD\) nên \(\widehat {ACB} = \widehat {CAD} + \widehat {CDA}\)
Lại có \(\Delta CAD\) cân tại \(C \Rightarrow \widehat {CAD} = \widehat {CDA} = x\) (tính chất)
Nên \(\widehat {ACB} = \widehat {CAD} + \widehat {CDA} = 2x \Rightarrow x = \dfrac{{\widehat {ACB}}}{2}\)\( = \dfrac{{70^\circ }}{2} = 35^\circ .\)
Vậy \(x = 35^\circ .\)
Số tam giác cân trong hình vẽ dưới đây là:

\(2\)
\(1\)
\(3\)
\(4\)
Đáp án : A
Từ hình vẽ ta có \(AB = AE;BC = DE\)
Vì \(AB = AE \Rightarrow \Delta ABE\) cân tại \(A.\)
Suy ra \(\widehat B = \widehat E\) (hai góc ở đáy)
Xét tam giác \(ABC\) và \(AED\) có: \(AB = AE;\widehat B = \widehat E\left( {cmt} \right);BC = DE\) nên \(\Delta ABC = \Delta AED\left( {c - g - c} \right)\)
Do đó \(AC = AD\) (hai cạnh tương ứng) suy ra \(\Delta ACD\) cân tại \(A.\)
Vậy có hai tam giác cân trên hình vẽ.
Một tam giác cân có góc ở đáy bằng \({70^0}\) thì số đo góc ở đỉnh là:
\({54^0}\)
\({63^0}\)
\({70^0}\)
\({40^0}\)
Đáp án : D
Sử dụng tính chất tổng ba góc của một tam giác và sử dụng tính chất của tam giác cân.
Tổng số đo hai góc ở đáy là \(70^o.2 = 140^\circ \)
Vì tổng ba góc của tam giác bằng \(180^\circ \) nên số đo góc ở đỉnh tam giác cân này là
\(180^\circ - 140^\circ = 40^\circ .\)
Một tam giác cân có góc ở đỉnh bằng \({64^0}\) thì số đo góc ở đáy là:
\({54^0}\)
\({58^0}\)
\({72^0}\)
\({90^0}\)
Đáp án : B
Sử dụng tính chất tổng ba góc của một tam giác và sử dụng tính chất của tam giác cân.
Sử dụng cách tính số đo các góc trong tam giác $ABC$ cân tại $A.$
Góc ở đỉnh \(\widehat A = {180^0} - 2\widehat C\) và góc ở đáy \(\widehat C = \dfrac{{{{180}^0} - \widehat A}}{2}.\)
Áp dụng ta có số đo góc ở đáy bằng: $\dfrac{{{{180}^0} - {{64}^0}}}{2} = {58^0}$
Cho tam giác $ABC$ cân tại $A.$ Phát biểu nào trong các phát biểu sau là sai:
\(\widehat B = \widehat C\)
\(\widehat C = \dfrac{{{{180}^0} - \widehat A}}{2}\)
\(\widehat A = {180^0} - 2\widehat C\)
\(\widehat B \ne \widehat C\)
Đáp án : D
+ Áp dụng tính chất của tam giác cân và tính chất tổng các góc của một tam giác
Do tam giác ABC cân nên \(\widehat B = \widehat C\)
Xét tam giác ABC ta có: \(\widehat A + \widehat B + \widehat C = {180^0} \Leftrightarrow \widehat B + \widehat C = {180^0} - \widehat A \Leftrightarrow \widehat C = \dfrac{{{{180}^0} - \widehat A}}{2}\) hay \(\widehat A = {180^0} - 2\widehat C\)
Hai góc nhọn của tam giác vuông cân bằng nhau và bằng
\(30^\circ \)
\(45^\circ \)
\(60^\circ \)
\(90^\circ \)
Đáp án : B
Mỗi góc nhọn của tam giác vuông cân bằng \({45^0}.\)
Chọn câu sai.
Tam giác đều có ba góc bằng nhau và bằng \(60^\circ .\)
Tam giác đều có ba cạnh bằng nhau.
Tam giác cân là tam giác đều.
Tam giác đều là tam giác cân.
Đáp án : C
Tam giác đều là tam giác có ba cạnh bằng nhau.
Trong tam giác đều, mỗi góc bằng \({60^0}.\)
Nên A, B đúng.
Tam giác đều cũng là tam giác cân nhưng tam giác cân chưa chắc là tam giác đều vì nó chỉ có hai cạnh bên bằng nhau.
Vậy C sai.
Tam giác cân là một trong những khái niệm cơ bản và quan trọng trong hình học lớp 7. Hiểu rõ về tam giác cân, các tính chất và định lý liên quan là nền tảng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Tam giác cân là tam giác có hai cạnh bằng nhau. Hai cạnh bằng nhau được gọi là cạnh bên, cạnh còn lại được gọi là cạnh đáy. Góc đối diện với cạnh đáy được gọi là góc đỉnh, hai góc còn lại được gọi là góc đáy.
Dưới đây là một số câu hỏi trắc nghiệm minh họa cho Bài 7: Tam giác cân Toán 7 Cánh diều. Hãy thử sức và kiểm tra kiến thức của bạn!
(A) 30 độ (B) 60 độ (C) 90 độ (D) 120 độ)
(A) 40 độ (B) 50 độ (C) 60 độ (D) 70 độ)
(A) Là đường phân giác (B) Là đường cao (C) Là đường trung bình (D) Cả A và B)
(A) 5cm (B) 7cm (C) 6cm (D) Không xác định)
(A) Tam giác có ba cạnh khác nhau (B) Tam giác có hai cạnh bằng nhau (C) Tam giác vuông cân (D) Cả B và C)
Câu 1: Đáp án (B). Vì tam giác ABC cân tại A nên góc B = góc C = 60 độ.
Câu 2: Đáp án (B). Vì tam giác MNP cân tại M nên góc N = góc P = 40 độ.
Câu 3: Đáp án (D). Đường trung tuyến kẻ từ đỉnh của tam giác cân xuống cạnh đáy đồng thời là đường phân giác và đường cao.
Câu 4: Đáp án (A). Vì tam giác DEF cân tại D nên DE = DF = 5cm.
Câu 5: Đáp án (D). Tam giác cân là tam giác có hai cạnh bằng nhau, tam giác vuông cân cũng là một dạng của tam giác cân.
Để hiểu sâu hơn về tam giác cân và các bài toán liên quan, các em có thể tham khảo thêm các tài liệu sau:
Chúc các em học tốt và đạt kết quả cao trong môn Toán!