Bài viết này cung cấp bộ câu hỏi trắc nghiệm giúp học sinh ôn luyện và kiểm tra kiến thức về tính chất ba đường trung tuyến của tam giác trong chương trình Toán 7 Cánh diều. Các câu hỏi được thiết kế đa dạng, bao gồm nhiều mức độ khó khác nhau, kèm theo đáp án và lời giải chi tiết.
Giaitoan.edu.vn luôn đồng hành cùng học sinh trong quá trình học tập, cung cấp tài liệu học tập chất lượng và phương pháp giải bài tập hiệu quả.
Cho \(\Delta ABC.\) Trên tia đối của tia \(BC\) lấy điểm \(E,\) trên tia đối của tia \(CB\) lấy điểm \(F\) sao cho \(BE = CF.\) Gọi \(G\) là trọng tâm tam giác \(ABC.\)\(AG\) cắt \(BC\) tại \(M\). Lấy \(H\) là trung điểm \(AG.\) Nối \(EG\) cắt \(AF\) tại \(N.\) Lấy \(I\) là trung điểm \(EG.\)
Chọn câu đúng.
Hai tam giác \(ABC\) và \(AEF\) có cùng trọng tâm
Hai tam giác \(ABC\) và \(AEC\) có cùng trọng tâm
Hai tam giác \(ABC\) và \(ABF\) có cùng trọng tâm
Hai tam giác \(AEM\) và \(AMF\) có cùng trọng tâm
Chọn câu đúng.
\(IH//MN;IH = MN\)
\(IH//MN;IH < MN\)
\(IH//MN;IH > MN\)
\(IH//MN;IH = 2MN\)
Cho tam giác $MNP,$ hai đường trung tuyến $ME$ và $NF$ cắt nhau tại $O.$ Tính diện tích tam giác $MNP,$ biết diện tích tam giác $MNO$ là \(8c{m^2}\).
$12\,c{m^2}$
\(48\,c{m^2}\)
\(36\,c{m^2}\)
\(24\,c{m^2}\)
Cho tam giác $ABC$ vuông tại $A$ có $AB = 5cm,BC = 13cm$ . Ba đường trung tuyến $AM,BN,CE$ cắt nhau tại $O.$
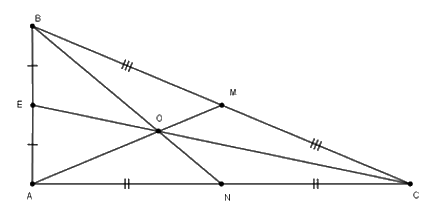
Độ dài trung tuyến $BN$ là :
$6cm\;$
\(\sqrt {61} \,cm\)
$12cm$
\(\sqrt {65} \,cm\)
Cho tam giác \(ABC\), đường trung tuyến \(BD\). Trên tia đối của tia $DB$ lấy điểm \(E\) sao cho \(DE = DB.\) Gọi \(M,N\) theo thứ tự là trung điểm của \(BC;CE.\) Gọi \(I;K\) theo thứ tự là giao điểm của \(AM,AN\) với \(BE.\) Chọn câu đúng.
\(BI = IK > KE\)
\(BI > IK > KE\)
\(BI = IK = KE\)
\(BI < IK < KE\)
Cho tam giác \(ABC\), các đường trung tuyến \(BD\) và \(CE\). Chọn câu đúng.
\(BD + CE < \dfrac{3}{2}BC\)
\(BD + CE > \dfrac{3}{2}BC\)
\(BD + CE = \dfrac{3}{2}BC\)
\(BD + CE = BC\)
Cho tam giác $ABC$ có các đường trung tuyến \(BD\) và \(CE\) vuông góc với nhau. Tính độ dài cạnh \(BC\) biết \(BD = 9\,cm;\,CE = 12\,cm.\)
\(BC = 12\,cm.\)
\(BC = 6\,cm.\)
\(BC = 8\,cm.\)
\(BC = 10\,cm.\)
Cho tam giác \(ABC\) có hai đường trung tuyến \(BD;CE\) sao cho \(BD = CE\). Khi đó tam giác \(ABC\)
Cân tại \(B.\)
Cân tại \(C.\)
Vuông tại \(A.\)
Cân tại \(A.\)
Cho \(G\) là trọng tâm của tam giác đều. Chọn câu đúng.
\(GA = GB = GC\)
\(GA = GB > GC\)
\(GA < GB < GC\)
\(GA > GB > GC\)
Tam giác \(ABC\) có trung tuyến \(AM = 9\,cm\) và trọng tâm \(G\). Độ dài đoạn \(AG\) là
\(4,5\,cm\)
\(3\,cm\)
\(6\,cm\)
\(4\,cm\)
Cho hình vẽ sau:
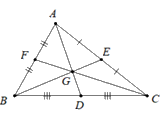
Điền số thích hợp vào chỗ chấm: \(BG = ...BE\)
$2$
$3$
\(\dfrac{1}{3}\)
\(\dfrac{2}{3}\)
Điền số thích hợp vào chỗ chấm: $AG = \ldots GD$
$2$
$3$
\(\dfrac{1}{3}\)
\(\dfrac{2}{3}\)
Điền số thích hợp vào chỗ chấm: “Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng … độ dài đường trung tuyến đi qua đỉnh ấy”
\(\dfrac{2}{3}\)
\(\dfrac{3}{2}\)
\(3\)
\(2\)
Chọn câu sai.
Trong một tam giác có ba đường trung tuyến
Các đường trung tuyến của tam giác cắt nhau tại một điểm.
Giao của ba đường trung tuyến của một tam giác gọi là trọng tâm của tam giác đó.
Một tam giác có hai trọng tâm
Lời giải và đáp án
Cho \(\Delta ABC.\) Trên tia đối của tia \(BC\) lấy điểm \(E,\) trên tia đối của tia \(CB\) lấy điểm \(F\) sao cho \(BE = CF.\) Gọi \(G\) là trọng tâm tam giác \(ABC.\)\(AG\) cắt \(BC\) tại \(M\). Lấy \(H\) là trung điểm \(AG.\) Nối \(EG\) cắt \(AF\) tại \(N.\) Lấy \(I\) là trung điểm \(EG.\)
Chọn câu đúng.
Hai tam giác \(ABC\) và \(AEF\) có cùng trọng tâm
Hai tam giác \(ABC\) và \(AEC\) có cùng trọng tâm
Hai tam giác \(ABC\) và \(ABF\) có cùng trọng tâm
Hai tam giác \(AEM\) và \(AMF\) có cùng trọng tâm
Đáp án: A
+ Chứng minh \(ME = MF\), từ đó suy ra \(AM\) là đường trung tuyến ứng với cạnh \(EF\) của \(\Delta AEF\)
+ Sử dụng định lý về tính chất ba đường trung tuyến của tam giác: Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\) độ dài đường trung tuyến đi qua đỉnh ấy.
+ Khi đó ta chứng minh được G là trọng tâm \(\Delta AEF\).
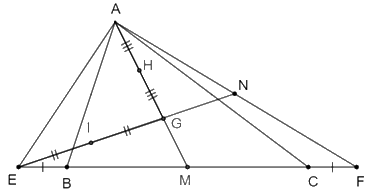
Ta có: \(MB = MC\) (vì \(AM\) là đường trung tuyến ứng với cạnh \(BC\) của \(\Delta ABC)\); \(BE = CF\) (gt)
Mà \(ME = MB + BE;MF = MC + CF\)
Suy ra \(ME = MF\).
Do đó \(AM\) là đường trung tuyến ứng với cạnh \(EF\) của \(\Delta AEF\)
Mặt khác \(AG = \dfrac{2}{3}AM\) (do G là trọng tâm \(\Delta ABC)\)
Vậy G là trọng tâm \(\Delta AEF\).
Chọn câu đúng.
\(IH//MN;IH = MN\)
\(IH//MN;IH < MN\)
\(IH//MN;IH > MN\)
\(IH//MN;IH = 2MN\)
Đáp án: A
+ Chứng minh \(GI = GN\); \(GH = GM\)
+ Chứng minh \(\Delta GHI = \Delta GMN\,(c.g.c)\), từ đó suy ra \(HI = MN\)
+ Dựa vào dấu hiệu nhận biết hai đường thẳng song song, chứng minh \(HI//MN\): Nếu đường thẳng \(c\) cắt hai đường thẳng \(a,b\) và trong các góc tạo thành có một cặp góc so le trong bằng nhau (hoặc một cặp góc đồng vị bằng nhau) thì \(a,b\) song song với nhau.
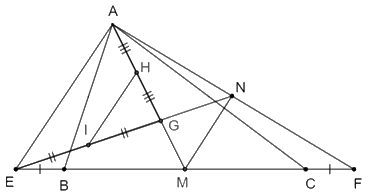
Theo câu trước ta có: \(G\) là trọng tâm \(\Delta AEF\) nên \(EG = \dfrac{2}{3}EN\) (tính chất ba đường trung tuyến của tam giác)
Mà \(GI = \dfrac{1}{2}EG\) (vì \(I\) là trung điểm của \(EG\))
Suy ra \(GI = \dfrac{1}{2}.\dfrac{2}{3}EN = \dfrac{1}{3}EN\)
Mặt khác \(GN = \dfrac{1}{3}EN\) (vì \(G\) là trọng tâm \(\Delta AEF\))
Do đó \(GI = GN\).
Theo câu trước ta có: \(AG = \dfrac{2}{3}AM\) mà \(GH = \dfrac{1}{2}AG\) (vì \(H\) là trung điểm của \(AG\))
Suy ra \(GH = \dfrac{1}{2}.\dfrac{2}{3}AM = \dfrac{1}{3}AM\)
Mặt khác \(GM = \dfrac{1}{3}AM\) (vì \(G\) là trọng tâm \(\Delta AEF\))
Do đó \(GH = GM\).
Xét \(\Delta GHI\) và \(\Delta GMN\) có:
\(GI = GN\) (cmt)
\(\widehat {HGI} = \widehat {NGM}\) (hai góc đối đỉnh)
\(GH = GM\) (cmt)
Vậy \(\Delta GHI = \Delta GMN\,(c.g.c)\) \(\Rightarrow HI = MN\) (hai cạnh tương ứng); \(\widehat {IHG} = \widehat {NMG}\) (hai góc tương ứng)
Mà \(\widehat {IHG};\widehat {NMG}\) ở vị trí so le trong nên \(HI//MN\).
Cho tam giác $MNP,$ hai đường trung tuyến $ME$ và $NF$ cắt nhau tại $O.$ Tính diện tích tam giác $MNP,$ biết diện tích tam giác $MNO$ là \(8c{m^2}\).
$12\,c{m^2}$
\(48\,c{m^2}\)
\(36\,c{m^2}\)
\(24\,c{m^2}\)
Đáp án : D
+) Dựa vào đinh lý về tính chất ba đường trung tuyến của một tam giác để tìm mối liên hệ giữa các cạnh.
+) Áp dụng công thức tính diện tích của một tam giác.
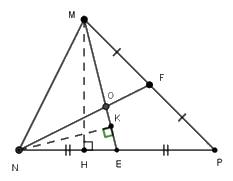
Gọi $MH$ là đường cao kẻ từ $M$ xuống cạnh $BC,NK$ là đường cao kẻ từ $N$ xuống cạnh $ME.$
Hai đường trung tuyến $ME$ và $NF$ cắt nhau tại $O$ nên $O$ là trọng tâm tam giác $MNP,$ do đó \(MO = \dfrac{2}{3}ME\).
Có $ME$ là đường trung tuyến ứng với cạnh $NP$ nên $E$ là trung điểm của $NP,$ suy ra $NP = 2.NE$
Ta có:
\(\dfrac{{{S_{MNO}}}}{{{S_{MNE}}}} = \dfrac{{\dfrac{1}{2}.NK.MO}}{{\dfrac{1}{2}.NK.ME}} = \dfrac{{\dfrac{1}{2}.NK.\dfrac{2}{3}.ME}}{{\dfrac{1}{2}.NK.ME}} = \dfrac{2}{3}\) \(\Rightarrow {S_{MNO}} = \dfrac{2}{3}{S_{MNE}}\)
\(\dfrac{{{S_{MNE}}}}{{{S_{MNP}}}} = \dfrac{{\dfrac{1}{2}.MH.NE}}{{\dfrac{1}{2}.MH.NP}} = \dfrac{{\dfrac{1}{2}.MH.NE}}{{\dfrac{1}{2}.MH.2.NE}} = \dfrac{1}{2}\) \( \Rightarrow {S_{MNE}} = \dfrac{1}{2}{S_{MNP}}\)
Từ đó suy ra
\({S_{MNP}} = 2.{S_{MNE}} = 3.{S_{MNO}}\) \( \Rightarrow {S_{MNP}} = 3.8 = 24\,c{m^2}\)
Cho tam giác $ABC$ vuông tại $A$ có $AB = 5cm,BC = 13cm$ . Ba đường trung tuyến $AM,BN,CE$ cắt nhau tại $O.$
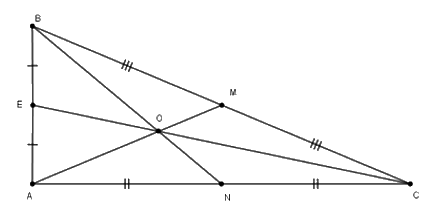
Độ dài trung tuyến $BN$ là :
$6cm\;$
\(\sqrt {61} \,cm\)
$12cm$
\(\sqrt {65} \,cm\)
Đáp án : B
+) Sử dụng định lý Py-ta-go để tính cạnh của tam giác vuông
+) Dựa vào đinh lý về tính chất ba đường trung tuyến của một tam giác để tính độ dài cạnh theo đề bài yêu cầu
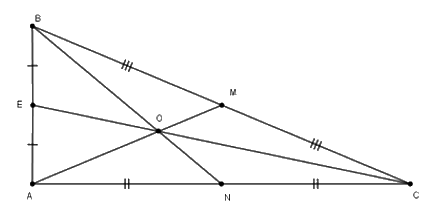
\(\Delta ABC\)vuông tại $A$ nên theo định lí Py-ta-go ta có:
\(A{B^2} + A{C^2} = B{C^2}\) \(\Rightarrow A{C^2} = B{C^2} - A{B^2} = {13^2} - {5^2} = 144\)\( \Rightarrow AC = 12\,cm\)
Ta có $AM,BN,CE$ là các đường trung tuyến ứng với các cạnh $BC,AC,AB$ của tam giác vuông $ABC$
Suy ra $M,N,E$ lần lượt là trung điểm của các cạnh $BC,AC,AB.$
$ \Rightarrow AN = \dfrac{1}{2}AC = \dfrac{1}{2} \cdot 12 = 6\,cm$
Áp dụng định lí Py-ta-go với tam giác $ABN$ vuông tại $A$ ta có: $A{B^2} + A{N^2} = B{N^2} $ $\Rightarrow {5^2} + {6^2} = B{N^2} \Rightarrow B{N^2} = 61$$ \Rightarrow BN = \sqrt {61} \,cm$
Cho tam giác \(ABC\), đường trung tuyến \(BD\). Trên tia đối của tia $DB$ lấy điểm \(E\) sao cho \(DE = DB.\) Gọi \(M,N\) theo thứ tự là trung điểm của \(BC;CE.\) Gọi \(I;K\) theo thứ tự là giao điểm của \(AM,AN\) với \(BE.\) Chọn câu đúng.
\(BI = IK > KE\)
\(BI > IK > KE\)
\(BI = IK = KE\)
\(BI < IK < KE\)
Đáp án : C
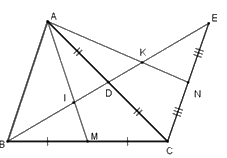
\(I\) là trọng tâm tam giác \(ABC\) nên \(BI = \dfrac{2}{3}BD = \dfrac{1}{3}BE\) \(\left( 1 \right)\)
\(K\) là trọng tâm tam giác \(ACE\) nên \(EK = \dfrac{2}{3}ED = \dfrac{1}{3}BE\,\,\,\left( 2 \right)\)
Từ \(\left( 1 \right);\left( 2 \right)\) suy ra \(IK = \dfrac{1}{3}BE\) từ đó \(BI = EK = IK\) .
Cho tam giác \(ABC\), các đường trung tuyến \(BD\) và \(CE\). Chọn câu đúng.
\(BD + CE < \dfrac{3}{2}BC\)
\(BD + CE > \dfrac{3}{2}BC\)
\(BD + CE = \dfrac{3}{2}BC\)
\(BD + CE = BC\)
Đáp án : B
+ Sử dụng tính chất đường trung tuyến của tam giác và quan hệ giữa các cạnh trong tam giác
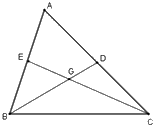
Gọi \(G\) là giao điểm của \(BD\) và \(CE\). Trong \(\Delta GBC\) ta có \(BG + CG > BC\)
Ta lại có \(BG = \dfrac{2}{3}BD;\,CG = \dfrac{2}{3}CE\) (tính chất các đường trung tuyến của tam giác \(ABC\))
Từ đó \(\dfrac{2}{3}BD + \dfrac{2}{3}CE > BG + CG\)\( \Rightarrow \dfrac{2}{3}\left( {BD + CE} \right) > BC\)\( \Rightarrow BD + CE > \dfrac{3}{2}BC.\)
Cho tam giác $ABC$ có các đường trung tuyến \(BD\) và \(CE\) vuông góc với nhau. Tính độ dài cạnh \(BC\) biết \(BD = 9\,cm;\,CE = 12\,cm.\)
\(BC = 12\,cm.\)
\(BC = 6\,cm.\)
\(BC = 8\,cm.\)
\(BC = 10\,cm.\)
Đáp án : D
+ Dựa vào đinh lý về tính chất ba đường trung tuyến của một tam giác để tính \(BG;CG.\)
+ Sử dụng định lý Pytago để tính cạnh \(BC.\)
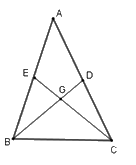
Gọi giao điểm của hai đường trung tuyến \(BD\) và \(CE\) là \(G\) thì \(G\) là trọng tâm tam giác \(ABC.\)
Theo tính chất đường trung tuyến của tam giác ta có \(BG = \dfrac{2}{3}BD;\,CG = \dfrac{2}{3}CE\)
Mà \(BD = 9\,cm;\,CE = 12\,cm\) nên \(BG = \dfrac{2}{3}.9 = 6\,cm;\,CG = \dfrac{2}{3}.12\,cm = 8\,cm.\)
Xét tam giác \(BGC\) vuông tại $G,$ theo định lý Pytago ta có
\(B{C^2} = B{G^2} + C{G^2}\)
\(B{C^2} = {6^2} + {8^2} = 100\) hay \(BC = 10\,cm.\)
Vậy \(BC = 10\,cm.\)
Cho tam giác \(ABC\) có hai đường trung tuyến \(BD;CE\) sao cho \(BD = CE\). Khi đó tam giác \(ABC\)
Cân tại \(B.\)
Cân tại \(C.\)
Vuông tại \(A.\)
Cân tại \(A.\)
Đáp án : D
+ Sử dụng tính chất về đường trung tuyến của tam giác
+ Chứng minh hai tam giác bằng nhau \(\Delta BGE = \Delta CGD\left( {c - g - c} \right)\)
+ Từ đó suy ra tính chất của tam giác \(ABC.\)
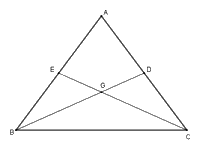
Hai đường trung tuyến \(BD;CE\) cắt nhau tại \(G\) suy ra \(G\) là trọng tâm tam giác \(ABC.\)
Suy ra \(BG = \dfrac{2}{3}BD;\,CG = \dfrac{2}{3}CE\) mà \(BD = CE \Rightarrow \)\(BG = CG.\) Từ đó \(BD - BG = CE - CG \Rightarrow GD = GE\)
Xét tam giác \(BGE\) và tam giác \(CGD\) có
+ \(BG = CG\)
+ \(\widehat {BGE} = \widehat {CGD}\) (đối đỉnh)
+ \(GD = GE\)
Nên \(\Delta BGE = \Delta CGD\left( {c - g - c} \right)\) suy ra \(BE = CD \Rightarrow \dfrac{1}{2}AB = \dfrac{1}{2}AC\) do đó \(AB = AC\) hay tam giác $ABC$ cân tại \(A.\)
Cho \(G\) là trọng tâm của tam giác đều. Chọn câu đúng.
\(GA = GB = GC\)
\(GA = GB > GC\)
\(GA < GB < GC\)
\(GA > GB > GC\)
Đáp án : A
Chứng minh $D,E,F$ theo thứ tự là trung điểm của $BC,AC,AB.$
Kết hợp với $BC = AC = AB$ (do tam giác $ABC$ là tam giác đều) ta được $BD = DC = CE = EA = AF = FB$
Chứng minh \(\Delta AEB = AFC\,(c.g.c)\), suy ra $BE = CF$
Chứng minh \(\Delta BEC = ADC\,(c.g.c)\), suy ra $BE = AD$
Do đó $AD = BE = CF$
Sử dụng tính chất của trọng tâm của tam giác để chứng minh $GA = GB = GC.$
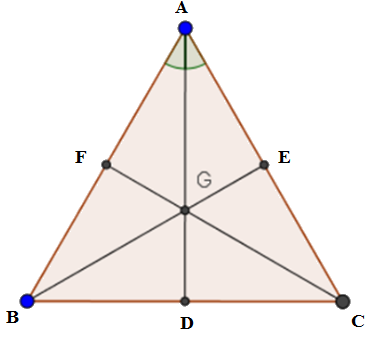
Các tia $AG,BG$ và $CG$ cắt $BC,AC,AB$ lần lượt tại $D,E,F$ thì $D,E,F$ theo thứ tự là trung điểm của $BC,AC,AB.$
Mà $BC = AC = AB$ (do tam giác $ABC$ là tam giác đều), do đó $BD = DC = CE = EA = AF = FB$
Xét \(\Delta AEB\) và \(\Delta AFC\) ta có: $AB = AC;$ \(\widehat A\) chung; $AE = AF.$
Vậy \(\Delta AEB = AFC\,(c.g.c)\), suy ra $BE = CF\,\,\,\,\left( 1 \right)$
Chứng minh tương tự ta có \(\Delta BEC = ADC\,(c.g.c)\), suy ra $BE = AD\left( 2 \right)$
Từ (1) và (2) ta có: $AD = BE = CF\left( 3 \right)$
Theo đề bài $G$ là trọng tâm của tam giác $ABC$ nên ta có:
\(GA = \dfrac{2}{3}AD;\,\,GB = \dfrac{2}{3}BE;\,\,GC = \dfrac{2}{3}CF\)
Vì thế từ (3) ta suy ra $GA = GB = GC.$
Tam giác \(ABC\) có trung tuyến \(AM = 9\,cm\) và trọng tâm \(G\). Độ dài đoạn \(AG\) là
\(4,5\,cm\)
\(3\,cm\)
\(6\,cm\)
\(4\,cm\)
Đáp án : C
Vì \(G\) là trọng tâm tam giác \(ABC\) và \(AM\) là đường trung tuyến nên \(AG = \dfrac{2}{3}AM\) (tính chất ba đường trung tuyến của tam giác)
Do đó $AG = \dfrac{2}{3}.9 = 6\,cm.$
Cho hình vẽ sau:
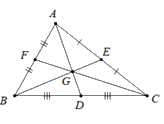
Điền số thích hợp vào chỗ chấm: \(BG = ...BE\)
$2$
$3$
\(\dfrac{1}{3}\)
\(\dfrac{2}{3}\)
Đáp án: D
Ta có $AD;BE$ và $CF$ là ba đường trung tuyến của tam giác $ABC$ và chúng cắt nhau tại $G$ nên $G$ là trọng tâm của tam giác \(ABC\) .
Theo tính chất ba đường trung tuyến của tam giác ta có : \(\dfrac{{BG}}{{BE}} = \dfrac{2}{3} \Rightarrow BG = \dfrac{2}{3}BE\).
Vậy số thích hợp điền vào chỗ chấm là \(\dfrac{2}{3}.\)
Điền số thích hợp vào chỗ chấm: $AG = \ldots GD$
$2$
$3$
\(\dfrac{1}{3}\)
\(\dfrac{2}{3}\)
Đáp án: A
Theo câu trước ta có $G$ là trọng tâm của tam giác \(ABC\) .
Theo tính chất ba đường trung tuyến của tam giác ta có : \(\dfrac{{AG}}{{AD}} = \dfrac{2}{3} \Rightarrow \dfrac{{AG}}{{GD}} = 2 \Rightarrow AG = 2GD\).
Vậy số thích hợp điền vào chỗ chấm là $2.$
Điền số thích hợp vào chỗ chấm: “Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng … độ dài đường trung tuyến đi qua đỉnh ấy”
\(\dfrac{2}{3}\)
\(\dfrac{3}{2}\)
\(3\)
\(2\)
Đáp án : A
Định lý: Vị trí trọng tâm: Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\) độ dài đường trung tuyến đi qua đỉnh ấy.
Số cần điền là \(\dfrac{2}{3}.\)
Chọn câu sai.
Trong một tam giác có ba đường trung tuyến
Các đường trung tuyến của tam giác cắt nhau tại một điểm.
Giao của ba đường trung tuyến của một tam giác gọi là trọng tâm của tam giác đó.
Một tam giác có hai trọng tâm
Đáp án : D
Sử dụng kiến thức về ba đường trung tuyến.
“ Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm gặp nhau của ba đường trung tuyến gọi là trọng tâm của tam giác đó.”
+ Một tam giác chỉ có một trọng tâm nên đáp án D sai.
Bài 10 trong chương trình Toán 7 Cánh diều tập trung vào việc tìm hiểu và vận dụng tính chất của ba đường trung tuyến trong một tam giác. Đường trung tuyến là đoạn thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện. Việc nắm vững tính chất của ba đường trung tuyến không chỉ giúp giải quyết các bài toán hình học cơ bản mà còn là nền tảng cho các kiến thức nâng cao hơn.
Trước khi đi vào giải các bài tập trắc nghiệm, chúng ta cần ôn lại một số kiến thức lý thuyết quan trọng:
Các bài tập trắc nghiệm về tính chất ba đường trung tuyến thường xoay quanh các chủ đề sau:
Dưới đây là một số câu hỏi trắc nghiệm mẫu để bạn luyện tập:
Câu 1: Trong tam giác ABC, M là trung điểm của BC. Đường thẳng AM được gọi là:
Câu 2: G là trọng tâm của tam giác ABC. Biết AG = 6cm. Độ dài đoạn thẳng GM là:
Câu 3: Cho tam giác ABC có AB = 6cm, BC = 8cm, CA = 10cm. Gọi M là trung điểm của BC. Độ dài đoạn thẳng AM là:
Giải Câu 1: Đáp án C. Theo định nghĩa, đường trung tuyến của tam giác là đoạn thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện. Do đó, AM là đường trung tuyến của tam giác ABC.
Giải Câu 2: Đáp án A. Theo tính chất của trọng tâm, trọng tâm chia mỗi đường trung tuyến thành hai đoạn thẳng có tỉ lệ 2:1, tính từ đỉnh. Vậy GM = (1/2)AG = (1/2) * 6cm = 3cm.
Giải Câu 3: Ta nhận thấy 62 + 82 = 36 + 64 = 100 = 102. Vậy tam giác ABC vuông tại B. Trong tam giác vuông, trung tuyến ứng với cạnh huyền có độ dài bằng nửa cạnh huyền. Do đó, AM = BC/2 = 8cm/2 = 4cm.
Để hiểu sâu hơn về tính chất ba đường trung tuyến, bạn có thể tìm hiểu thêm về:
Hy vọng với bộ câu hỏi trắc nghiệm này, bạn sẽ nắm vững kiến thức về tính chất ba đường trung tuyến của tam giác và tự tin hơn trong các bài kiểm tra Toán 7.