Bài viết này cung cấp bộ câu hỏi trắc nghiệm giúp học sinh ôn luyện và kiểm tra kiến thức về tính chất ba đường phân giác trong tam giác, thuộc chương trình Toán 7 Cánh diều.
Các câu hỏi được thiết kế đa dạng, bao gồm nhiều mức độ khó khác nhau, từ dễ đến khó, giúp học sinh rèn luyện kỹ năng giải bài tập và hiểu sâu hơn về lý thuyết.
Giaitoan.edu.vn luôn đồng hành cùng học sinh trên con đường chinh phục môn Toán.
Cho tam giác \(ABC\) có phân giác \(AD\) thỏa mãn \(BD = 2DC.\) Trên tia đối tia \(CB\) lấy điểm \(E\) sao cho \(BC = CE.\) Khi đó tam giác \(ADE\) là tam giác:
Cân tại A
Vuông tại \(D\)
Vuông tại \(A\)
Vuông tại \(E\)
Cho tam giác \(ABC\) có: \(\widehat B = 2\widehat C,\) các đường phân giác của góc \(B\) và \(C\) cắt nhau tại \(I.\) Chọn câu đúng.
\(AC = AB + IB\)
\(AC = AB + IA\)
\(AC = AB + IC\)
\(AC = BC + IB\)
Cho tam giác \(ABC\) có \(\widehat A = 120^\circ \). Các đường phân giác $AD$ và \(BE.\) Tính số đo góc \(BED.\)
\({55^0}\)
\({45^0}\)
\({60^0}\)
\({30^0}\)
Cho tam giác \(ABC\) có \(AH \bot BC\) và \(\widehat {BAH} = 2.\widehat C\) . Tia phân giác của góc \(B\) cắt \(AC\) ở \(E.\) Tia phân giác của góc \(BAH\) cắt \(BE\) ở \(I.\) Khi đó tam giác \(AIE\) là tam giác
Vuông cân tại \(I\)
Vuông cân tại \(E\)
Vuông cân tại \(A\)
Cân tại \(I\)
Cho \(\Delta ABC\) cân tại $A,$ trung tuyến $AM.$ Gọi $D$ là một điểm nằm giữa $A$ và $M.$ Khi đó \(\Delta BDC\) là tam giác gì?
Tam giác cân
Tam giác đều
Tam giác vuông
Tam giác vuông cân.
Cho \(\Delta ABC\) cân tại A. Gọi G là trọng tâm của tam giác, I là giao điểm của các đường phân giác trong tam giác. Khi đó ta có:
I cách đều ba đỉnh của \(\Delta ABC\).
A, I, G thẳng hàng
G cách đều ba cạnh của \(\Delta ABC\).
Cả 3 đáp án trên đều đúng
Cho \(\Delta ABC\) có \(\widehat A = {90^0}\), các tia phân giác của \(\widehat B\)và \(\widehat C\)cắt nhau tại I. Gọi $D,E$ là chân các đường vuông góc hạ từ $I$ đến các cạnh $AB$ và $AC.$ Khi đó ta có:
AI là đường cao của \(\Delta ABC\).
\(IA = IB = IC\)
AI là đường trung tuyến của \(\Delta ABC\)
\(ID = IE\).
Cho \(\Delta ABC\), các tia phân giác của góc $B$ và $A$ cắt nhau tại điểm $O.$ Qua $O$ kẻ đường thẳng song song với $BC$ cắt $AB$ tại $M,$ cắt $AC$ ở $N.$ Cho $BM = 2cm,CN = 3cm.$ Tính $MN?$
$5cm$
$6cm$
$7cm$
$8cm$
Cho \(\Delta ABC\) có \(\widehat A = {70^0}\), các đường phân giác $BE$ và $CD$ của \(\widehat B\) và \(\widehat C\) cắt nhau tại $I.$ Tính \(\widehat {BIC}\)?
\({125^0}\)
\({100^0}\)
\({105^0}\)
\({140^0}\)
Em hãy chọn câu đúng nhất:
Ba tia phân giác của một tam giác cùng đi qua một điểm. Điểm đó gọi là trọng tâm của tam giác
Giao điểm của ba đường phân giác của tam giác cách đều ba cạnh của tam giác
Trong một tam giác, đường trung tuyến xuất phát từ đỉnh cũng đồng thời là đường phân giác ứng với cạnh đáy
Giao điểm của ba đường phân giác của tam giác là tâm đường tròn ngoại tiếp tam giác đó
Cho tam giác \(ABC\) có hai đường phân giác \(CD\) và \(BE\) cắt nhau tại \(I.\) Khi đó
\(AI\) là trung tuyến vẽ từ \(A.\)
\(AI\) là đường cao kẻ từ \(A.\)
\(AI\) là trung trực cạnh \(BC.\)
\(AI\) là phân giác của góc \(A.\)
Điểm \(E\) nằm trên tia phân giác góc \(A\) của tam giác \(ABC\) ta có
\(E\) nằm trên tia phân giác góc \(B\)
\(E\) cách đều hai cạnh \(AB,\,AC.\)
\(E\) nằm trên tia phân giác góc \(C.\)
\(EB = EC.\)
Lời giải và đáp án
Cho tam giác \(ABC\) có phân giác \(AD\) thỏa mãn \(BD = 2DC.\) Trên tia đối tia \(CB\) lấy điểm \(E\) sao cho \(BC = CE.\) Khi đó tam giác \(ADE\) là tam giác:
Cân tại A
Vuông tại \(D\)
Vuông tại \(A\)
Vuông tại \(E\)
Đáp án : C
+ Kéo dài \(AC\) lấy điểm \(M\) sao cho: \(CM = AC\), kéo dài \(AD\) cắt \(BM\) tại \(H\)
+ Chứng minh \(D\) là trọng tâm của \(\Delta ABM\), từ đó chứng minh \(\Delta ABM\) cân tại \(A\)
+ Chứng minh \(\widehat {AHB} = {90^0}\), từ đó suy ra \(AD \bot BM\)
+ Chứng minh \(\Delta ACE = \Delta MCB\,(c.g.c)\)
+ Chứng minh \(AE//BM\), từ đó suy ra tam giác \(ADE\) là tam giác gì.
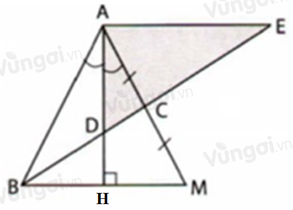
Kéo dài \(AC\) lấy điểm \(M\) sao cho: \(CM = AC\), kéo dài \(AD\) cắt \(BM\) tại \(H\)
Vì \(AD\) là phân giác của \(\widehat {BAM}\) nên \(\widehat {BAH} = \widehat {HAM} = \dfrac{{\widehat {BAM}}}{2}\) (tính chất tia phân giác)
Xét \(\Delta ABM\) có: \(BC\) là đường trung tuyến ứng với cạnh \(AM\), \(BD = 2DC\) (gt)
Do đó \(D\) là trọng tâm của \(\Delta ABM\)
Suy ra \(AD\) là đường trung tuyến của \(\Delta ABM\)
Xét \(\Delta ABM\) có: \(AD\) là đường trung tuyến đồng thời là đường phân giác
Do đó \(\Delta ABM\) cân tại \(A\) \( \Rightarrow \widehat {ABM} = \widehat {AMB}\) (tính chất tam giác cân)
Trong \(\Delta ABM\) có: \(\widehat {BAM} + \widehat {ABM} + \widehat {AMB} = {180^0}\) ( định lý tổng ba góc của tam giác)
\( \Rightarrow \widehat {BAM} + 2\widehat {ABM} = {180^0} \Rightarrow \dfrac{{\widehat {BAM}}}{2} + \widehat {ABM} = {90^0}\) hay \(\widehat {BAH} + \widehat {ABH} = {90^0}\)
Xét \(\Delta ABH\) có:
\(\widehat {BAH} + \widehat {ABH} + \widehat {AHB} = {180^0}\) (định lý tổng ba góc của tam giác)
\( \Rightarrow \widehat {AHB} = {180^0} - (\widehat {BAH} + \widehat {ABH}) = {180^0} - {90^0} = {90^0}\)
\( \Rightarrow AH \bot BM\) hay \(AD \bot BM\)
Xét \(\Delta ACE\) và \(\Delta MCB\) có:
\(AC = CM\)
\(BC = CE\,(gt)\)
\(\widehat {ACE} = \widehat {MCB}\) (hai góc đối đỉnh)
\( \Rightarrow \Delta ACE = \Delta MCB\,(c.g.c)\) \( \Rightarrow \widehat {AEC} = \widehat {MBC}\) (hai góc tương ứng)
Mà \(\widehat {AEC};\widehat {MBC}\) ở vị trí so le trong
\( \Rightarrow AE//BM\) (dấu hiệu nhận biết hai đường thẳng song song)
Mà \(AD \bot BM \Rightarrow AD \bot AE\) (quan hệ giữa tính vuông góc với tính song song)
Do đó \(\Delta ADE\) vuông tại \(A\).
Cho tam giác \(ABC\) có: \(\widehat B = 2\widehat C,\) các đường phân giác của góc \(B\) và \(C\) cắt nhau tại \(I.\) Chọn câu đúng.
\(AC = AB + IB\)
\(AC = AB + IA\)
\(AC = AB + IC\)
\(AC = BC + IB\)
Đáp án : A
+ Kẻ \(ID \bot BC;IE \bot AC;IF \bot AB\)
+ Sử dụng tính chất ba đường phân giác của tam giác, chứng minh \(AI\) là phân giác của \(\widehat {BAC}\)
+ Chứng minh \(BF = BD;\) \(AF = AE;CE = CD\)
+ Trên đoạn \(DC\) lấy điểm \(G\) sao cho \(BD = DG\), chứng minh \(IB = IG\)
+ Chứng minh \(IG//AC\)
+ Chứng minh \(IG = GC\)
+ Từ các điều trên ta tính được \(AC\).
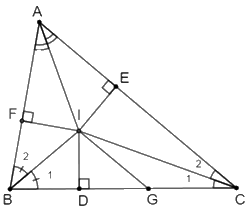
Kẻ \(ID \bot BC;IE \bot AC;IF \bot AB\)
Tam giác \(ABC\) có các đường phân giác của góc \(\widehat {ABC}\) và \(\widehat {ACB}\) cắt nhau tại \(I\) nên \(AI\) là phân giác của \(\widehat {BAC}\) (tính chất ba đường phân giác của tam giác)
Vì \(BI\) là tia phân giác của \(\widehat {ABC}\) nên \(\widehat {{B_1}} = \widehat {{B_2}} = \dfrac{{\widehat {ABC}}}{2}\) (tính chất tia phân giác)
Xét \(\Delta BFI\) vuông tại \(F\) và \(\Delta BDI\) vuông tại \(D\) có:
\(\widehat {{B_1}} = \widehat {{B_2}}\) (cmt)
\(BI\) là cạnh chung
Do đó \(\Delta BFI = \Delta BDI\) (cạnh huyền – góc nhọn) \( \Rightarrow BF = BD\) (hai cạnh tương ứng)
Chứng minh tương tự ta có: \(AF = AE;CE = CD\).
Trên đoạn \(DC\) lấy điểm \(G\) sao cho \(BD = DG\).
Xét \(\Delta BDI\) vuông tại \(D\) và \(\Delta GDI\) vuông tại \(D\) có:
\(BD = DG\) (theo cách vẽ)
\(DI\) là cạnh chung
Do đó \(\Delta BDI = \Delta GDI\) (hai cạnh góc vuông) \( \Rightarrow IB = IG\) (hai cạnh tương ứng) \( \Rightarrow \Delta IBG\) là tam giác cân tại \(I\)
\( \Rightarrow \widehat {{B_1}} = \widehat {IGB}\) (tính chất tam giác cân) \((1)\)
Ta có: \(\widehat {ABC} = 2\widehat {ACB} \Rightarrow \widehat {ACB} = \dfrac{{\widehat {ABC}}}{2} = \widehat {{B_1}}\) \((2)\)
Từ \((1)\); \((2)\) suy ra: \( \Rightarrow \widehat {IGB} = \widehat {ACB}\) mà hai góc này ở vị trí đồng vị nên \(IG//AC\) (dấu hiệu nhận biết hai đường thẳng song song)
Khi đó \(\widehat {{C_2}} = \widehat {GIC}\) (hai góc so le trong)
Mặt khác: \(\widehat {{C_2}} = \widehat {{C_1}}\) (do \(CI\) là tia phân giác của \(\widehat {ACB}\))
\( \Rightarrow \widehat {{C_1}} = \widehat {GIC} \Rightarrow \Delta GIC\) cân tại \(G\) \( \Rightarrow IG = GC\) (định nghĩa tam giác cân)
Ta có: \(AC = AE + CE\)
\(\begin{array}{l} = AF + CD\\ = AF + DG + GC\\ = AF + BD + IG\\ = AF + BF + IB\\ = AB + IB\end{array}\)
Cho tam giác \(ABC\) có \(\widehat A = 120^\circ \). Các đường phân giác $AD$ và \(BE.\) Tính số đo góc \(BED.\)
\({55^0}\)
\({45^0}\)
\({60^0}\)
\({30^0}\)
Đáp án : D
Áp dụng định lý về góc ngoài của một tam giác, tính chất tia phân giác của một góc.
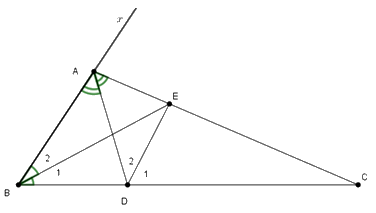
Gọi \(Ax\) là tia đối của tia \(AB.\) Ta có \(\widehat {BAD} = \widehat {DAC} = 60^\circ \) nên \(\widehat {CAx} = 60^\circ .\)
Xét \(\Delta ABD\) có \(AE\) là tia phân giác của góc ngoài đỉnh \(A,\)\(BE\) là tia phân giác của góc \(B\) và chúng cắt nhau tại \(E\) nên \(DE\) là phân giác góc ngoài của góc \(D.\)
Mà \(\widehat {EDC}\) là góc ngoài tại đỉnh \(D\) của tam giác \(BED\) nên \(\widehat {{B_1}} + \widehat {BED} = \widehat {EDC}\)
Do đó \(\widehat {BED} = \widehat {{D_1}} - \widehat {{B_1}} = \dfrac{{\widehat {ADC} - \widehat {ABC}}}{2} = \dfrac{{\widehat {BAD}}}{2} = 30^\circ \)
Cho tam giác \(ABC\) có \(AH \bot BC\) và \(\widehat {BAH} = 2.\widehat C\) . Tia phân giác của góc \(B\) cắt \(AC\) ở \(E.\) Tia phân giác của góc \(BAH\) cắt \(BE\) ở \(I.\) Khi đó tam giác \(AIE\) là tam giác
Vuông cân tại \(I\)
Vuông cân tại \(E\)
Vuông cân tại \(A\)
Cân tại \(I\)
Đáp án : C
+ Sử dụng tính chất đường phân giác của một góc
+ Sử dụng định lý về góc ngoài của một góc
+ Từ đó suy ra tính chất tam giác \(AIE.\)
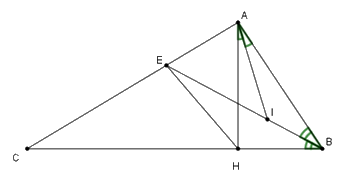
Xét tam giác \(AHB\) vuông ta có \(\widehat {BAH} + \widehat {ABH} = 90^\circ \) mà \(\widehat {BAH} = 2\widehat C\) và \(\widehat {ABH} = 2.\widehat {IBH}\)
Suy ra \(2\widehat C + 2.\widehat {IBH} = 90^\circ \Rightarrow 2\left( {\widehat C + \widehat {IBH}} \right) = 90^\circ \) \( \Rightarrow \widehat C + \widehat {EBH} = 45^\circ \) .
Xét tam giác \(BEC\) có \(\widehat {IEA}\) là góc ngoài tại đỉnh \(E\) nên \(\widehat {AEI} = \widehat {ECB} + \widehat {EBC} = 45^\circ \)
Xét tam giác \(AHB\) có \(\widehat {BAH} + \widehat {HBA} = 90^\circ \Rightarrow 2.\widehat {IAB} + 2.\widehat {IBA} = 90^\circ \)\( \Rightarrow \widehat {IAB} + \widehat {IBA} = 90^\circ :2\)
\( \Rightarrow \widehat {IAB} + \widehat {IBA} = 45^\circ \)
Xét tam giác \(AIB\) có \(\widehat {AIE}\) là góc ngoài tại đỉnh \(I\) nên \(\widehat {AIE} = \widehat {IAB} + \widehat {IBA} = 45^\circ \)
Xét tam giác \(IAE\) có \(\widehat {AIE} = 45^\circ = \widehat {AEI}\) suy ra \(\widehat {EAI} = 180^\circ - \widehat {AEI} - \widehat {AIE} = 90^\circ \) (tổng ba góc trong tam giác)
Nên tam giác \(IAE\) vuông cân tại \(A.\)
Cho \(\Delta ABC\) cân tại $A,$ trung tuyến $AM.$ Gọi $D$ là một điểm nằm giữa $A$ và $M.$ Khi đó \(\Delta BDC\) là tam giác gì?
Tam giác cân
Tam giác đều
Tam giác vuông
Tam giác vuông cân.
Đáp án : A
Áp dụng tính chất: Trong một tam giác cân, đường trung tuyến xuất phát từ đỉnh cũng đồng thời là đường phân giác ứng với cạnh đáy.
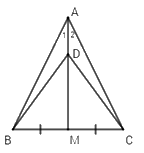
Vì \(\Delta ABC\) cân tại A (gt) và AM là trung tuyến nên AM cũng là đường phân giác của \(\widehat {BAC}\)
\( \Rightarrow \widehat {{A_1}} = \widehat {{A_2}}\) (tính chất tia phân giác)
Xét \(\Delta ABD\) và \(\Delta ACD\) có:
\(AB = AC\left( {gt} \right)\)
\(\widehat {{A_1}} = \widehat {{A_2}}\left( {cmt} \right)\)
AD chung
\( \Rightarrow \Delta ABD = \Delta ACD\left( {c - g - c} \right) \Rightarrow BD = DC\) (2 cạnh tương ứng)
\( \Rightarrow \Delta BDC\) cân tại D (dấu hiệu nhận biết tam giác cân)
Cho \(\Delta ABC\) cân tại A. Gọi G là trọng tâm của tam giác, I là giao điểm của các đường phân giác trong tam giác. Khi đó ta có:
I cách đều ba đỉnh của \(\Delta ABC\).
A, I, G thẳng hàng
G cách đều ba cạnh của \(\Delta ABC\).
Cả 3 đáp án trên đều đúng
Đáp án : B
Áp dụng tính chất:
Trong một tam giác cân, đường trung tuyến xuất phát từ đỉnh cũng đồng thời là đường phân giác ứng với cạnh đáy.
$I$ là giao điểm của các đường phân giác trong tam giác nên I cách đều 3 cạnh của tam giác. Loại đáp án A.
Ta có:\(\Delta ABC\) cân tại $A,I$ là giao điểm của các đường phân giác trong tam giác nên $AI$ vừa là đường trung tuyến đồng thời là đường phân giác của \(\widehat {BAC}\) . Mà $G$ là trọng tâm của \(\Delta ABC\) nên $A,G,I$ thẳng hàng. Chọn B.
Cho \(\Delta ABC\) có \(\widehat A = {90^0}\), các tia phân giác của \(\widehat B\)và \(\widehat C\)cắt nhau tại I. Gọi $D,E$ là chân các đường vuông góc hạ từ $I$ đến các cạnh $AB$ và $AC.$ Khi đó ta có:
AI là đường cao của \(\Delta ABC\).
\(IA = IB = IC\)
AI là đường trung tuyến của \(\Delta ABC\)
\(ID = IE\).
Đáp án : D
Áp dụng tính chất 3 đường phân giác của tam giác.
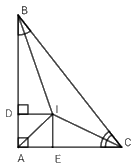
Xét \(\Delta ABC\) có các tia phân giác của \(\widehat B\)và \(\widehat C\)cắt nhau tại I nên I là giao điểm của ba đường phân giác trong \(\Delta ABC\), suy ra AI là đường phân giác của \(\widehat A\) và I cách đều ba cạnh của \(\Delta ABC\) (tính chất 3 đường phân giác của tam giác). Vậy ta loại đáp án A, B và C.
Vì I là giao điểm của ba đường phân giác trong \(\Delta ABC\) nên \( \Rightarrow DI = IE\) (tính chất 3 đường phân giác của tam giác).
Cho \(\Delta ABC\), các tia phân giác của góc $B$ và $A$ cắt nhau tại điểm $O.$ Qua $O$ kẻ đường thẳng song song với $BC$ cắt $AB$ tại $M,$ cắt $AC$ ở $N.$ Cho $BM = 2cm,CN = 3cm.$ Tính $MN?$
$5cm$
$6cm$
$7cm$
$8cm$
Đáp án : A
Áp dụng tính chất 3 đường phân giác của tam giác, tia phân giác của 1 góc, hai đường thẳng song song và tính chất tam giác cân.
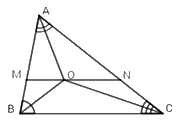
Vì O là giao điểm của hai tia phân giác của các góc \(\widehat {ABC}\) và \(\widehat {CAB}\)(gt)
Suy ra, CO là phân giác của \(\widehat {ACB}\)(tính chất 3 đường phân giác của tam giác)
\( \Rightarrow \widehat {ACO} = \widehat {BCO}\left( 1 \right)\) (tính chất tia phân giác của một góc)
BO là phân giác của \(\widehat {ABC}\left( {gt} \right) \Rightarrow \widehat {OBA} = \widehat {OBC}\left( 2 \right)\) (tính chất tia phân giác của một góc)
Vì MN // BC (gt) \(\left\{ \begin{array}{l}\widehat {MOB} = \widehat {OBC}\left( 3 \right)\\\widehat {NOC} = \widehat {OCB}\left( 4 \right)\end{array} \right.\) (so le trong)
Từ (1) và (4) \( \Rightarrow \widehat {NOC} = \widehat {NCO} \Rightarrow \Delta NOC\) cân tại N (dấu hiệu nhận biết tam giác cân)
\( \Rightarrow NO = NC = 3cm\) (tính chất tam giác cân)
Từ (2) và (3) \( \Rightarrow \widehat {MOB} = \widehat {MBO} \Rightarrow \Delta MOB\) cân tại M (dấu hiệu nhận biết tam giác cân)
\( \Rightarrow MB = MO = 2cm\) (tính chất tam giác cân)
\( \Rightarrow MN = MO + ON = 2 + 3 = 5cm.\)
Cho \(\Delta ABC\) có \(\widehat A = {70^0}\), các đường phân giác $BE$ và $CD$ của \(\widehat B\) và \(\widehat C\) cắt nhau tại $I.$ Tính \(\widehat {BIC}\)?
\({125^0}\)
\({100^0}\)
\({105^0}\)
\({140^0}\)
Đáp án : A
Áp dụng định lý tổng ba góc trong một tam giác, tính chất tia phân giác của một góc.
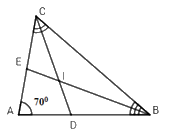
Xét \(\Delta ABC\) có: \(\widehat A + \widehat {ACB} + \widehat {ABC} = {180^0}\) (định lý tổng ba góc trong một tam giác)
\( \Rightarrow \widehat {ACB} + \widehat {ABC} = {180^0} - \widehat A = {180^0} - {70^0} = {110^0}\left( 1 \right)\)
Vì $CD$ là phân giác của \(\widehat {ACB}\left( {gt} \right) \Rightarrow \widehat {DCB} = \dfrac{{\widehat {ACB}}}{2}\left( 2 \right)\) (tính chất tia phân giác)
Vì $BE $ là phân giác của \(\widehat {ABC}\left( {gt} \right) \Rightarrow \widehat {CBE} = \dfrac{{\widehat {ABC}}}{2}\left( 3 \right)\) (tính chất tia phân giác)
Từ $(1), (2)$ và $(3)$ \( \Rightarrow \widehat {DCB} + \widehat {CBE} = \dfrac{{\widehat {ACB}}}{2} + \dfrac{{\widehat {ABC}}}{2} = \dfrac{{\widehat {ACB} + \widehat {ABC}}}{2} = {110^0}:2 = {55^0}\) hay \(\widehat {ICB} + \widehat {IBC} = {55^0}\left( * \right)\)
Xét \(\Delta BIC\) có: \(\widehat {ICB} + \widehat {IBC} + \widehat {BIC} = {180^0}\left( {**} \right)\)( định lý tổng ba góc trong một tam giác)
Từ (*) và (**) \( \Rightarrow \widehat {BIC} = {180^0} - \left( {\widehat {ICB} + \widehat {IBC}} \right) = {180^0} - {55^0} = {125^0}\)
Em hãy chọn câu đúng nhất:
Ba tia phân giác của một tam giác cùng đi qua một điểm. Điểm đó gọi là trọng tâm của tam giác
Giao điểm của ba đường phân giác của tam giác cách đều ba cạnh của tam giác
Trong một tam giác, đường trung tuyến xuất phát từ đỉnh cũng đồng thời là đường phân giác ứng với cạnh đáy
Giao điểm của ba đường phân giác của tam giác là tâm đường tròn ngoại tiếp tam giác đó
Đáp án : B
+ Trọng tâm là giao điểm của ba đường trung tuyến nên đáp án A sai. Loại đáp án A.
+ Giao điểm của ba đường phân giác của tam giác cách đều ba cạnh của tam giác là đúng. Chọn đáp án B.
+ Trong một tam giác, đường trung tuyến xuất phát từ đỉnh cũng đồng thời là đường phân giác ứng với cạnh đáy sai vì tính chất này không phải đúng với mọi tam giác. Loại đáp án C.
+ Giao điểm của ba đường phân giác của tam giác là tâm đường tròn ngoại tiếp tam giác đó sai vì giao điểm của ba đường phân giác của tam giác là tâm đường tròn nội tiếp tam giác đó. Loại đáp án D.
Cho tam giác \(ABC\) có hai đường phân giác \(CD\) và \(BE\) cắt nhau tại \(I.\) Khi đó
\(AI\) là trung tuyến vẽ từ \(A.\)
\(AI\) là đường cao kẻ từ \(A.\)
\(AI\) là trung trực cạnh \(BC.\)
\(AI\) là phân giác của góc \(A.\)
Đáp án : D
Hai đường phân giác \(CD\) và \(BE\) cắt nhau tại \(I\) mà ba đường phân giác của một tam giác cùng đi qua một điểm nên \(AI\) là phân giác của góc \(A.\)
Điểm \(E\) nằm trên tia phân giác góc \(A\) của tam giác \(ABC\) ta có
\(E\) nằm trên tia phân giác góc \(B\)
\(E\) cách đều hai cạnh \(AB,\,AC.\)
\(E\) nằm trên tia phân giác góc \(C.\)
\(EB = EC.\)
Đáp án : B
Sử dụng tính chất tia phân giác của một góc: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
Điểm \(E\) nằm trên tia phân giác góc \(A\) của tam giác \(ABC\) thì điểm \(E\) cách đều hai cạnh \(AB;AC.\)
Cho tam giác \(ABC\) có phân giác \(AD\) thỏa mãn \(BD = 2DC.\) Trên tia đối tia \(CB\) lấy điểm \(E\) sao cho \(BC = CE.\) Khi đó tam giác \(ADE\) là tam giác:
Cân tại A
Vuông tại \(D\)
Vuông tại \(A\)
Vuông tại \(E\)
Cho tam giác \(ABC\) có: \(\widehat B = 2\widehat C,\) các đường phân giác của góc \(B\) và \(C\) cắt nhau tại \(I.\) Chọn câu đúng.
\(AC = AB + IB\)
\(AC = AB + IA\)
\(AC = AB + IC\)
\(AC = BC + IB\)
Cho tam giác \(ABC\) có \(\widehat A = 120^\circ \). Các đường phân giác $AD$ và \(BE.\) Tính số đo góc \(BED.\)
\({55^0}\)
\({45^0}\)
\({60^0}\)
\({30^0}\)
Cho tam giác \(ABC\) có \(AH \bot BC\) và \(\widehat {BAH} = 2.\widehat C\) . Tia phân giác của góc \(B\) cắt \(AC\) ở \(E.\) Tia phân giác của góc \(BAH\) cắt \(BE\) ở \(I.\) Khi đó tam giác \(AIE\) là tam giác
Vuông cân tại \(I\)
Vuông cân tại \(E\)
Vuông cân tại \(A\)
Cân tại \(I\)
Cho \(\Delta ABC\) cân tại $A,$ trung tuyến $AM.$ Gọi $D$ là một điểm nằm giữa $A$ và $M.$ Khi đó \(\Delta BDC\) là tam giác gì?
Tam giác cân
Tam giác đều
Tam giác vuông
Tam giác vuông cân.
Cho \(\Delta ABC\) cân tại A. Gọi G là trọng tâm của tam giác, I là giao điểm của các đường phân giác trong tam giác. Khi đó ta có:
I cách đều ba đỉnh của \(\Delta ABC\).
A, I, G thẳng hàng
G cách đều ba cạnh của \(\Delta ABC\).
Cả 3 đáp án trên đều đúng
Cho \(\Delta ABC\) có \(\widehat A = {90^0}\), các tia phân giác của \(\widehat B\)và \(\widehat C\)cắt nhau tại I. Gọi $D,E$ là chân các đường vuông góc hạ từ $I$ đến các cạnh $AB$ và $AC.$ Khi đó ta có:
AI là đường cao của \(\Delta ABC\).
\(IA = IB = IC\)
AI là đường trung tuyến của \(\Delta ABC\)
\(ID = IE\).
Cho \(\Delta ABC\), các tia phân giác của góc $B$ và $A$ cắt nhau tại điểm $O.$ Qua $O$ kẻ đường thẳng song song với $BC$ cắt $AB$ tại $M,$ cắt $AC$ ở $N.$ Cho $BM = 2cm,CN = 3cm.$ Tính $MN?$
$5cm$
$6cm$
$7cm$
$8cm$
Cho \(\Delta ABC\) có \(\widehat A = {70^0}\), các đường phân giác $BE$ và $CD$ của \(\widehat B\) và \(\widehat C\) cắt nhau tại $I.$ Tính \(\widehat {BIC}\)?
\({125^0}\)
\({100^0}\)
\({105^0}\)
\({140^0}\)
Em hãy chọn câu đúng nhất:
Ba tia phân giác của một tam giác cùng đi qua một điểm. Điểm đó gọi là trọng tâm của tam giác
Giao điểm của ba đường phân giác của tam giác cách đều ba cạnh của tam giác
Trong một tam giác, đường trung tuyến xuất phát từ đỉnh cũng đồng thời là đường phân giác ứng với cạnh đáy
Giao điểm của ba đường phân giác của tam giác là tâm đường tròn ngoại tiếp tam giác đó
Cho tam giác \(ABC\) có hai đường phân giác \(CD\) và \(BE\) cắt nhau tại \(I.\) Khi đó
\(AI\) là trung tuyến vẽ từ \(A.\)
\(AI\) là đường cao kẻ từ \(A.\)
\(AI\) là trung trực cạnh \(BC.\)
\(AI\) là phân giác của góc \(A.\)
Điểm \(E\) nằm trên tia phân giác góc \(A\) của tam giác \(ABC\) ta có
\(E\) nằm trên tia phân giác góc \(B\)
\(E\) cách đều hai cạnh \(AB,\,AC.\)
\(E\) nằm trên tia phân giác góc \(C.\)
\(EB = EC.\)
Cho tam giác \(ABC\) có phân giác \(AD\) thỏa mãn \(BD = 2DC.\) Trên tia đối tia \(CB\) lấy điểm \(E\) sao cho \(BC = CE.\) Khi đó tam giác \(ADE\) là tam giác:
Cân tại A
Vuông tại \(D\)
Vuông tại \(A\)
Vuông tại \(E\)
Đáp án : C
+ Kéo dài \(AC\) lấy điểm \(M\) sao cho: \(CM = AC\), kéo dài \(AD\) cắt \(BM\) tại \(H\)
+ Chứng minh \(D\) là trọng tâm của \(\Delta ABM\), từ đó chứng minh \(\Delta ABM\) cân tại \(A\)
+ Chứng minh \(\widehat {AHB} = {90^0}\), từ đó suy ra \(AD \bot BM\)
+ Chứng minh \(\Delta ACE = \Delta MCB\,(c.g.c)\)
+ Chứng minh \(AE//BM\), từ đó suy ra tam giác \(ADE\) là tam giác gì.

Kéo dài \(AC\) lấy điểm \(M\) sao cho: \(CM = AC\), kéo dài \(AD\) cắt \(BM\) tại \(H\)
Vì \(AD\) là phân giác của \(\widehat {BAM}\) nên \(\widehat {BAH} = \widehat {HAM} = \dfrac{{\widehat {BAM}}}{2}\) (tính chất tia phân giác)
Xét \(\Delta ABM\) có: \(BC\) là đường trung tuyến ứng với cạnh \(AM\), \(BD = 2DC\) (gt)
Do đó \(D\) là trọng tâm của \(\Delta ABM\)
Suy ra \(AD\) là đường trung tuyến của \(\Delta ABM\)
Xét \(\Delta ABM\) có: \(AD\) là đường trung tuyến đồng thời là đường phân giác
Do đó \(\Delta ABM\) cân tại \(A\) \( \Rightarrow \widehat {ABM} = \widehat {AMB}\) (tính chất tam giác cân)
Trong \(\Delta ABM\) có: \(\widehat {BAM} + \widehat {ABM} + \widehat {AMB} = {180^0}\) ( định lý tổng ba góc của tam giác)
\( \Rightarrow \widehat {BAM} + 2\widehat {ABM} = {180^0} \Rightarrow \dfrac{{\widehat {BAM}}}{2} + \widehat {ABM} = {90^0}\) hay \(\widehat {BAH} + \widehat {ABH} = {90^0}\)
Xét \(\Delta ABH\) có:
\(\widehat {BAH} + \widehat {ABH} + \widehat {AHB} = {180^0}\) (định lý tổng ba góc của tam giác)
\( \Rightarrow \widehat {AHB} = {180^0} - (\widehat {BAH} + \widehat {ABH}) = {180^0} - {90^0} = {90^0}\)
\( \Rightarrow AH \bot BM\) hay \(AD \bot BM\)
Xét \(\Delta ACE\) và \(\Delta MCB\) có:
\(AC = CM\)
\(BC = CE\,(gt)\)
\(\widehat {ACE} = \widehat {MCB}\) (hai góc đối đỉnh)
\( \Rightarrow \Delta ACE = \Delta MCB\,(c.g.c)\) \( \Rightarrow \widehat {AEC} = \widehat {MBC}\) (hai góc tương ứng)
Mà \(\widehat {AEC};\widehat {MBC}\) ở vị trí so le trong
\( \Rightarrow AE//BM\) (dấu hiệu nhận biết hai đường thẳng song song)
Mà \(AD \bot BM \Rightarrow AD \bot AE\) (quan hệ giữa tính vuông góc với tính song song)
Do đó \(\Delta ADE\) vuông tại \(A\).
Cho tam giác \(ABC\) có: \(\widehat B = 2\widehat C,\) các đường phân giác của góc \(B\) và \(C\) cắt nhau tại \(I.\) Chọn câu đúng.
\(AC = AB + IB\)
\(AC = AB + IA\)
\(AC = AB + IC\)
\(AC = BC + IB\)
Đáp án : A
+ Kẻ \(ID \bot BC;IE \bot AC;IF \bot AB\)
+ Sử dụng tính chất ba đường phân giác của tam giác, chứng minh \(AI\) là phân giác của \(\widehat {BAC}\)
+ Chứng minh \(BF = BD;\) \(AF = AE;CE = CD\)
+ Trên đoạn \(DC\) lấy điểm \(G\) sao cho \(BD = DG\), chứng minh \(IB = IG\)
+ Chứng minh \(IG//AC\)
+ Chứng minh \(IG = GC\)
+ Từ các điều trên ta tính được \(AC\).

Kẻ \(ID \bot BC;IE \bot AC;IF \bot AB\)
Tam giác \(ABC\) có các đường phân giác của góc \(\widehat {ABC}\) và \(\widehat {ACB}\) cắt nhau tại \(I\) nên \(AI\) là phân giác của \(\widehat {BAC}\) (tính chất ba đường phân giác của tam giác)
Vì \(BI\) là tia phân giác của \(\widehat {ABC}\) nên \(\widehat {{B_1}} = \widehat {{B_2}} = \dfrac{{\widehat {ABC}}}{2}\) (tính chất tia phân giác)
Xét \(\Delta BFI\) vuông tại \(F\) và \(\Delta BDI\) vuông tại \(D\) có:
\(\widehat {{B_1}} = \widehat {{B_2}}\) (cmt)
\(BI\) là cạnh chung
Do đó \(\Delta BFI = \Delta BDI\) (cạnh huyền – góc nhọn) \( \Rightarrow BF = BD\) (hai cạnh tương ứng)
Chứng minh tương tự ta có: \(AF = AE;CE = CD\).
Trên đoạn \(DC\) lấy điểm \(G\) sao cho \(BD = DG\).
Xét \(\Delta BDI\) vuông tại \(D\) và \(\Delta GDI\) vuông tại \(D\) có:
\(BD = DG\) (theo cách vẽ)
\(DI\) là cạnh chung
Do đó \(\Delta BDI = \Delta GDI\) (hai cạnh góc vuông) \( \Rightarrow IB = IG\) (hai cạnh tương ứng) \( \Rightarrow \Delta IBG\) là tam giác cân tại \(I\)
\( \Rightarrow \widehat {{B_1}} = \widehat {IGB}\) (tính chất tam giác cân) \((1)\)
Ta có: \(\widehat {ABC} = 2\widehat {ACB} \Rightarrow \widehat {ACB} = \dfrac{{\widehat {ABC}}}{2} = \widehat {{B_1}}\) \((2)\)
Từ \((1)\); \((2)\) suy ra: \( \Rightarrow \widehat {IGB} = \widehat {ACB}\) mà hai góc này ở vị trí đồng vị nên \(IG//AC\) (dấu hiệu nhận biết hai đường thẳng song song)
Khi đó \(\widehat {{C_2}} = \widehat {GIC}\) (hai góc so le trong)
Mặt khác: \(\widehat {{C_2}} = \widehat {{C_1}}\) (do \(CI\) là tia phân giác của \(\widehat {ACB}\))
\( \Rightarrow \widehat {{C_1}} = \widehat {GIC} \Rightarrow \Delta GIC\) cân tại \(G\) \( \Rightarrow IG = GC\) (định nghĩa tam giác cân)
Ta có: \(AC = AE + CE\)
\(\begin{array}{l} = AF + CD\\ = AF + DG + GC\\ = AF + BD + IG\\ = AF + BF + IB\\ = AB + IB\end{array}\)
Cho tam giác \(ABC\) có \(\widehat A = 120^\circ \). Các đường phân giác $AD$ và \(BE.\) Tính số đo góc \(BED.\)
\({55^0}\)
\({45^0}\)
\({60^0}\)
\({30^0}\)
Đáp án : D
Áp dụng định lý về góc ngoài của một tam giác, tính chất tia phân giác của một góc.

Gọi \(Ax\) là tia đối của tia \(AB.\) Ta có \(\widehat {BAD} = \widehat {DAC} = 60^\circ \) nên \(\widehat {CAx} = 60^\circ .\)
Xét \(\Delta ABD\) có \(AE\) là tia phân giác của góc ngoài đỉnh \(A,\)\(BE\) là tia phân giác của góc \(B\) và chúng cắt nhau tại \(E\) nên \(DE\) là phân giác góc ngoài của góc \(D.\)
Mà \(\widehat {EDC}\) là góc ngoài tại đỉnh \(D\) của tam giác \(BED\) nên \(\widehat {{B_1}} + \widehat {BED} = \widehat {EDC}\)
Do đó \(\widehat {BED} = \widehat {{D_1}} - \widehat {{B_1}} = \dfrac{{\widehat {ADC} - \widehat {ABC}}}{2} = \dfrac{{\widehat {BAD}}}{2} = 30^\circ \)
Cho tam giác \(ABC\) có \(AH \bot BC\) và \(\widehat {BAH} = 2.\widehat C\) . Tia phân giác của góc \(B\) cắt \(AC\) ở \(E.\) Tia phân giác của góc \(BAH\) cắt \(BE\) ở \(I.\) Khi đó tam giác \(AIE\) là tam giác
Vuông cân tại \(I\)
Vuông cân tại \(E\)
Vuông cân tại \(A\)
Cân tại \(I\)
Đáp án : C
+ Sử dụng tính chất đường phân giác của một góc
+ Sử dụng định lý về góc ngoài của một góc
+ Từ đó suy ra tính chất tam giác \(AIE.\)

Xét tam giác \(AHB\) vuông ta có \(\widehat {BAH} + \widehat {ABH} = 90^\circ \) mà \(\widehat {BAH} = 2\widehat C\) và \(\widehat {ABH} = 2.\widehat {IBH}\)
Suy ra \(2\widehat C + 2.\widehat {IBH} = 90^\circ \Rightarrow 2\left( {\widehat C + \widehat {IBH}} \right) = 90^\circ \) \( \Rightarrow \widehat C + \widehat {EBH} = 45^\circ \) .
Xét tam giác \(BEC\) có \(\widehat {IEA}\) là góc ngoài tại đỉnh \(E\) nên \(\widehat {AEI} = \widehat {ECB} + \widehat {EBC} = 45^\circ \)
Xét tam giác \(AHB\) có \(\widehat {BAH} + \widehat {HBA} = 90^\circ \Rightarrow 2.\widehat {IAB} + 2.\widehat {IBA} = 90^\circ \)\( \Rightarrow \widehat {IAB} + \widehat {IBA} = 90^\circ :2\)
\( \Rightarrow \widehat {IAB} + \widehat {IBA} = 45^\circ \)
Xét tam giác \(AIB\) có \(\widehat {AIE}\) là góc ngoài tại đỉnh \(I\) nên \(\widehat {AIE} = \widehat {IAB} + \widehat {IBA} = 45^\circ \)
Xét tam giác \(IAE\) có \(\widehat {AIE} = 45^\circ = \widehat {AEI}\) suy ra \(\widehat {EAI} = 180^\circ - \widehat {AEI} - \widehat {AIE} = 90^\circ \) (tổng ba góc trong tam giác)
Nên tam giác \(IAE\) vuông cân tại \(A.\)
Cho \(\Delta ABC\) cân tại $A,$ trung tuyến $AM.$ Gọi $D$ là một điểm nằm giữa $A$ và $M.$ Khi đó \(\Delta BDC\) là tam giác gì?
Tam giác cân
Tam giác đều
Tam giác vuông
Tam giác vuông cân.
Đáp án : A
Áp dụng tính chất: Trong một tam giác cân, đường trung tuyến xuất phát từ đỉnh cũng đồng thời là đường phân giác ứng với cạnh đáy.

Vì \(\Delta ABC\) cân tại A (gt) và AM là trung tuyến nên AM cũng là đường phân giác của \(\widehat {BAC}\)
\( \Rightarrow \widehat {{A_1}} = \widehat {{A_2}}\) (tính chất tia phân giác)
Xét \(\Delta ABD\) và \(\Delta ACD\) có:
\(AB = AC\left( {gt} \right)\)
\(\widehat {{A_1}} = \widehat {{A_2}}\left( {cmt} \right)\)
AD chung
\( \Rightarrow \Delta ABD = \Delta ACD\left( {c - g - c} \right) \Rightarrow BD = DC\) (2 cạnh tương ứng)
\( \Rightarrow \Delta BDC\) cân tại D (dấu hiệu nhận biết tam giác cân)
Cho \(\Delta ABC\) cân tại A. Gọi G là trọng tâm của tam giác, I là giao điểm của các đường phân giác trong tam giác. Khi đó ta có:
I cách đều ba đỉnh của \(\Delta ABC\).
A, I, G thẳng hàng
G cách đều ba cạnh của \(\Delta ABC\).
Cả 3 đáp án trên đều đúng
Đáp án : B
Áp dụng tính chất:
Trong một tam giác cân, đường trung tuyến xuất phát từ đỉnh cũng đồng thời là đường phân giác ứng với cạnh đáy.
$I$ là giao điểm của các đường phân giác trong tam giác nên I cách đều 3 cạnh của tam giác. Loại đáp án A.
Ta có:\(\Delta ABC\) cân tại $A,I$ là giao điểm của các đường phân giác trong tam giác nên $AI$ vừa là đường trung tuyến đồng thời là đường phân giác của \(\widehat {BAC}\) . Mà $G$ là trọng tâm của \(\Delta ABC\) nên $A,G,I$ thẳng hàng. Chọn B.
Cho \(\Delta ABC\) có \(\widehat A = {90^0}\), các tia phân giác của \(\widehat B\)và \(\widehat C\)cắt nhau tại I. Gọi $D,E$ là chân các đường vuông góc hạ từ $I$ đến các cạnh $AB$ và $AC.$ Khi đó ta có:
AI là đường cao của \(\Delta ABC\).
\(IA = IB = IC\)
AI là đường trung tuyến của \(\Delta ABC\)
\(ID = IE\).
Đáp án : D
Áp dụng tính chất 3 đường phân giác của tam giác.

Xét \(\Delta ABC\) có các tia phân giác của \(\widehat B\)và \(\widehat C\)cắt nhau tại I nên I là giao điểm của ba đường phân giác trong \(\Delta ABC\), suy ra AI là đường phân giác của \(\widehat A\) và I cách đều ba cạnh của \(\Delta ABC\) (tính chất 3 đường phân giác của tam giác). Vậy ta loại đáp án A, B và C.
Vì I là giao điểm của ba đường phân giác trong \(\Delta ABC\) nên \( \Rightarrow DI = IE\) (tính chất 3 đường phân giác của tam giác).
Cho \(\Delta ABC\), các tia phân giác của góc $B$ và $A$ cắt nhau tại điểm $O.$ Qua $O$ kẻ đường thẳng song song với $BC$ cắt $AB$ tại $M,$ cắt $AC$ ở $N.$ Cho $BM = 2cm,CN = 3cm.$ Tính $MN?$
$5cm$
$6cm$
$7cm$
$8cm$
Đáp án : A
Áp dụng tính chất 3 đường phân giác của tam giác, tia phân giác của 1 góc, hai đường thẳng song song và tính chất tam giác cân.

Vì O là giao điểm của hai tia phân giác của các góc \(\widehat {ABC}\) và \(\widehat {CAB}\)(gt)
Suy ra, CO là phân giác của \(\widehat {ACB}\)(tính chất 3 đường phân giác của tam giác)
\( \Rightarrow \widehat {ACO} = \widehat {BCO}\left( 1 \right)\) (tính chất tia phân giác của một góc)
BO là phân giác của \(\widehat {ABC}\left( {gt} \right) \Rightarrow \widehat {OBA} = \widehat {OBC}\left( 2 \right)\) (tính chất tia phân giác của một góc)
Vì MN // BC (gt) \(\left\{ \begin{array}{l}\widehat {MOB} = \widehat {OBC}\left( 3 \right)\\\widehat {NOC} = \widehat {OCB}\left( 4 \right)\end{array} \right.\) (so le trong)
Từ (1) và (4) \( \Rightarrow \widehat {NOC} = \widehat {NCO} \Rightarrow \Delta NOC\) cân tại N (dấu hiệu nhận biết tam giác cân)
\( \Rightarrow NO = NC = 3cm\) (tính chất tam giác cân)
Từ (2) và (3) \( \Rightarrow \widehat {MOB} = \widehat {MBO} \Rightarrow \Delta MOB\) cân tại M (dấu hiệu nhận biết tam giác cân)
\( \Rightarrow MB = MO = 2cm\) (tính chất tam giác cân)
\( \Rightarrow MN = MO + ON = 2 + 3 = 5cm.\)
Cho \(\Delta ABC\) có \(\widehat A = {70^0}\), các đường phân giác $BE$ và $CD$ của \(\widehat B\) và \(\widehat C\) cắt nhau tại $I.$ Tính \(\widehat {BIC}\)?
\({125^0}\)
\({100^0}\)
\({105^0}\)
\({140^0}\)
Đáp án : A
Áp dụng định lý tổng ba góc trong một tam giác, tính chất tia phân giác của một góc.

Xét \(\Delta ABC\) có: \(\widehat A + \widehat {ACB} + \widehat {ABC} = {180^0}\) (định lý tổng ba góc trong một tam giác)
\( \Rightarrow \widehat {ACB} + \widehat {ABC} = {180^0} - \widehat A = {180^0} - {70^0} = {110^0}\left( 1 \right)\)
Vì $CD$ là phân giác của \(\widehat {ACB}\left( {gt} \right) \Rightarrow \widehat {DCB} = \dfrac{{\widehat {ACB}}}{2}\left( 2 \right)\) (tính chất tia phân giác)
Vì $BE $ là phân giác của \(\widehat {ABC}\left( {gt} \right) \Rightarrow \widehat {CBE} = \dfrac{{\widehat {ABC}}}{2}\left( 3 \right)\) (tính chất tia phân giác)
Từ $(1), (2)$ và $(3)$ \( \Rightarrow \widehat {DCB} + \widehat {CBE} = \dfrac{{\widehat {ACB}}}{2} + \dfrac{{\widehat {ABC}}}{2} = \dfrac{{\widehat {ACB} + \widehat {ABC}}}{2} = {110^0}:2 = {55^0}\) hay \(\widehat {ICB} + \widehat {IBC} = {55^0}\left( * \right)\)
Xét \(\Delta BIC\) có: \(\widehat {ICB} + \widehat {IBC} + \widehat {BIC} = {180^0}\left( {**} \right)\)( định lý tổng ba góc trong một tam giác)
Từ (*) và (**) \( \Rightarrow \widehat {BIC} = {180^0} - \left( {\widehat {ICB} + \widehat {IBC}} \right) = {180^0} - {55^0} = {125^0}\)
Em hãy chọn câu đúng nhất:
Ba tia phân giác của một tam giác cùng đi qua một điểm. Điểm đó gọi là trọng tâm của tam giác
Giao điểm của ba đường phân giác của tam giác cách đều ba cạnh của tam giác
Trong một tam giác, đường trung tuyến xuất phát từ đỉnh cũng đồng thời là đường phân giác ứng với cạnh đáy
Giao điểm của ba đường phân giác của tam giác là tâm đường tròn ngoại tiếp tam giác đó
Đáp án : B
+ Trọng tâm là giao điểm của ba đường trung tuyến nên đáp án A sai. Loại đáp án A.
+ Giao điểm của ba đường phân giác của tam giác cách đều ba cạnh của tam giác là đúng. Chọn đáp án B.
+ Trong một tam giác, đường trung tuyến xuất phát từ đỉnh cũng đồng thời là đường phân giác ứng với cạnh đáy sai vì tính chất này không phải đúng với mọi tam giác. Loại đáp án C.
+ Giao điểm của ba đường phân giác của tam giác là tâm đường tròn ngoại tiếp tam giác đó sai vì giao điểm của ba đường phân giác của tam giác là tâm đường tròn nội tiếp tam giác đó. Loại đáp án D.
Cho tam giác \(ABC\) có hai đường phân giác \(CD\) và \(BE\) cắt nhau tại \(I.\) Khi đó
\(AI\) là trung tuyến vẽ từ \(A.\)
\(AI\) là đường cao kẻ từ \(A.\)
\(AI\) là trung trực cạnh \(BC.\)
\(AI\) là phân giác của góc \(A.\)
Đáp án : D
Hai đường phân giác \(CD\) và \(BE\) cắt nhau tại \(I\) mà ba đường phân giác của một tam giác cùng đi qua một điểm nên \(AI\) là phân giác của góc \(A.\)
Điểm \(E\) nằm trên tia phân giác góc \(A\) của tam giác \(ABC\) ta có
\(E\) nằm trên tia phân giác góc \(B\)
\(E\) cách đều hai cạnh \(AB,\,AC.\)
\(E\) nằm trên tia phân giác góc \(C.\)
\(EB = EC.\)
Đáp án : B
Sử dụng tính chất tia phân giác của một góc: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
Điểm \(E\) nằm trên tia phân giác góc \(A\) của tam giác \(ABC\) thì điểm \(E\) cách đều hai cạnh \(AB;AC.\)
Bài 11 trong chương trình Toán 7 Cánh diều tập trung vào tính chất quan trọng của ba đường phân giác trong một tam giác. Để nắm vững kiến thức này, việc luyện tập thông qua các bài tập trắc nghiệm là vô cùng cần thiết. Dưới đây là bộ câu hỏi trắc nghiệm được thiết kế chi tiết, kèm theo đáp án và lời giải thích để giúp các em học sinh hiểu rõ hơn về chủ đề này.
Trước khi đi vào phần trắc nghiệm, chúng ta cùng ôn lại một số kiến thức cơ bản về đường phân giác của tam giác:
Các bài tập trắc nghiệm về tính chất ba đường phân giác thường xoay quanh các dạng sau:
Dưới đây là một số câu hỏi trắc nghiệm minh họa, kèm theo đáp án và lời giải chi tiết:
Câu 1: Cho tam giác ABC, AD là đường phân giác của góc BAC (D thuộc BC). Biết AB = 6cm, AC = 8cm, BD = 3cm. Tính độ dài DC?
A. 4cm B. 5cm C. 6cm D. 7cm
Đáp án: A
Giải thích: Áp dụng tính chất đường phân giác, ta có: AB/AC = BD/DC => 6/8 = 3/DC => DC = (3 * 8) / 6 = 4cm
Câu 2: Trong tam giác ABC, ba đường phân giác AD, BE, CF đồng quy tại điểm I. Khẳng định nào sau đây là đúng?
A. I là trọng tâm của tam giác ABC. B. I là tâm đường tròn ngoại tiếp của tam giác ABC. C. I là tâm đường tròn nội tiếp của tam giác ABC. D. I là điểm cách đều ba đỉnh của tam giác ABC.
Đáp án: C
Giải thích: Theo tính chất ba đường phân giác đồng quy, điểm đồng quy là tâm đường tròn nội tiếp của tam giác.
Câu 3: Cho tam giác ABC cân tại A, đường phân giác AD (D thuộc BC). Khẳng định nào sau đây là đúng?
A. AD là đường trung tuyến. B. AD là đường cao. C. AD là đường trung trực. D. Cả A, B, C đều đúng.
Đáp án: D
Giải thích: Trong tam giác cân, đường phân giác xuất phát từ đỉnh góc cân đồng thời là đường trung tuyến và đường cao.
Để giải các bài tập trắc nghiệm về tính chất ba đường phân giác một cách hiệu quả, các em có thể tham khảo một số mẹo sau:
Hy vọng bộ câu hỏi trắc nghiệm này sẽ giúp các em học sinh ôn luyện và nắm vững kiến thức về tính chất ba đường phân giác của tam giác Toán 7 Cánh diều. Chúc các em học tập tốt!