Chào mừng các em học sinh đến với bài kiểm tra trắc nghiệm Bài 1: Góc ở vị trí đặc biệt môn Toán 7 chương trình Cánh diều. Bài trắc nghiệm này được thiết kế để giúp các em ôn tập và củng cố kiến thức đã học về các loại góc đặc biệt và mối quan hệ giữa chúng.
Giaitoan.edu.vn cung cấp bộ đề trắc nghiệm đa dạng, kèm đáp án chi tiết và lời giải thích dễ hiểu, giúp các em tự tin hơn trong quá trình học tập.
Hai đường thẳng zz’ và tt’ cắt nhau tại $A$. Góc đối đỉnh với \(\widehat {zAt'}\) là:
\(\widehat {z'At'}\)
\(\widehat {z'At}\)
\(\widehat {zAt'}\) \(\)
\(\widehat {zAt}\)
Cho góc \(xBy\) đối đỉnh với góc \(x'By'\) và \(\widehat {xBy} = 60^\circ \) . Tính số đo góc \(x'By'.\)
$30^\circ$
$120^\circ$
$90^\circ$
$60^\circ$
Cho hai đường thẳng \(xx'\) và \(yy'\) giao nhau tại \(O\) sao cho \(\widehat {xOy} = 45^\circ \) . Chọn câu sai.
$\widehat {x'Oy} = 135^\circ $
$\widehat {x'Oy'} = 45^\circ $
$\widehat {xOy'} = 135^\circ $
$\widehat {x'Oy'} = 135^\circ $
Cho cặp góc đối đỉnh \(\widehat {tOz}\) và \(\widehat {t'Oz'}\) (\(Oz\) và $Oz'$ là hai tia đối nhau). Biết \(\widehat {tOz'} = 4.\widehat {tOz}\). Tính các góc \(\widehat {tOz}\) và \(\widehat {t'Oz'}.\)
\(\widehat {zOt} = \widehat {z'Ot'} = 72^\circ \)
\(\widehat {zOt} = \widehat {z'Ot'} = 30^\circ \)
\(\widehat {zOt} = \widehat {z'Ot'} = 36^\circ \)
\(\widehat {zOt} = 72^\circ ;\,\widehat {z'Ot'} = 36^\circ \)
Vẽ góc $xOy$ có số đo bằng $35^\circ$. Vẽ góc $x'Oy'$ đối đỉnh với góc $xOy.$ Viết tên các góc có số đo bằng $145^o.$
\(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy'}\)
\(\widehat {xOy}\,\,;\,\,\widehat {x'Oy'}\)
\(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy}\)
\(\widehat {xOy'}\,\,;\,\,\widehat {xOy}\)
Hai đường thẳng \(AB\) và \(CD\) cắt nhau tại $O$ tạo thành \(\widehat {AOC} = 60^\circ \) . Gọi \(OM\) là phân giác \(\widehat {AOC}\) và \(ON\) là tia đối của tia \(OM\). Tính \(\widehat {BON}\) và \(\widehat {DON}.\)
\(\widehat {BON} = \widehat {DON} = 25^\circ \)
\(\widehat {BON} = \widehat {DON} = 30^\circ \)
\(\widehat {BON} = \widehat {DON} = 60^\circ \)
\(\widehat {BON} = \widehat {DON} = 45^\circ \)
Hai đường thẳng $AB$ và $CD$ cắt nhau tại $O.$ Biết \(\widehat {AOC} - \widehat {AOD} = {50^0}.\) Chọn câu đúng.
\(\widehat {AOC} = 110^\circ \)
\(\widehat {BOC} = 65^\circ \)
\(\widehat {BOD} = 120^\circ \)
\(\widehat {AOD} = 50^\circ \)
Hai đường thẳng zz’ và tt’ cắt nhau tại \(A\). Góc đối đỉnh với \(\widehat {zAt'}\) là:
\(\widehat {z'At'}\)
\(\widehat {z'At}\)
\(\widehat {zAt'}\)
\(\widehat {zAt}\)
Cho hai đường thẳng \(xx'\) và \(yy'\) cắt nhau tại \(O\) sao cho \(\widehat {xOy} = 135^\circ \) . Chọn câu đúng:
\(\widehat {x'Oy} = 135^\circ \)
\(\widehat {x'Oy'} = 45^\circ \)
\(\widehat {xOy'} = 135^\circ \)
\(\widehat {x'Oy'} = 135^\circ \)
Cho 2 đường thẳng ab và cd cắt nhau tại M ( tia Ma đối tia Mb). Biết \(\widehat {aMc} = 5.\widehat {bMc}\). Tính số đo \(\widehat {aMc}\) ?
30\(^\circ \)
36\(^\circ \)
144\(^\circ \)
150\(^\circ \)
Cho \(\widehat {ABC} = {56^o}\). Vẽ \(\widehat {ABC'}\) kề bù với \(\widehat {ABC}\); \(\widehat {C'BA'}\) kề bù với \(\widehat {ABC'}\). Tính số đo \(\widehat {C'BA'}\).
124o
142o
65o
56o
Vẽ góc \(xOy\) có số đo bằng 125o. Vẽ góc \(x'Oy'\) đối đỉnh với góc \(xOy.\) Viết tên các góc có số đo bằng 55o.
\(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy'}\)
\(\widehat {xOy}\,\,;\,\,\widehat {x'Oy'}\)
\(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy}\)
\(\widehat {xOy'}\,\,;\,\,\widehat {xOy}\)
Cho tia Ok là tia phân giác của \(\widehat {mOn}\)= 70o . Tính \(\widehat {nOk}\)
70o
140o
35o
110o
Cho hình vẽ sau. Biết góc $xOy'$ đối đỉnh với góc $x'Oy,$ biết \(\widehat {xOy'} = {\widehat O_1} = {165^o}\). Tính các góc đỉnh O (khác góc bẹt).
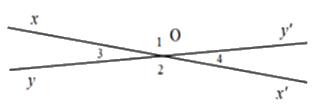
\({\widehat O_2} = {165^o};\,{\widehat O_3} = {15^o};\,\,{\widehat O_4} = {165^o}\,\,\)
\({\widehat O_2} = {165^o};\,{\widehat O_3} = {15^o};\,\,{\widehat O_4} = {15^o}\,\,\)
\({\widehat O_2} = {15^o};\,{\widehat O_3} = {15^o};\,\,{\widehat O_4} = {165^o}\,\,\)
\({\widehat O_2} = {15^o};\,{\widehat O_3} = {165^o};\,\,{\widehat O_4} = {15^o}\,\,\)
Lời giải và đáp án
Hai đường thẳng zz’ và tt’ cắt nhau tại $A$. Góc đối đỉnh với \(\widehat {zAt'}\) là:
\(\widehat {z'At'}\)
\(\widehat {z'At}\)
\(\widehat {zAt'}\) \(\)
\(\widehat {zAt}\)
Đáp án : B
Áp dụng định nghĩa hai góc đối đỉnh, xác định tia đối của tia \(Az\) và \(At'\), từ đó xác định góc đối đỉnh với \(\widehat {zAt'}\).
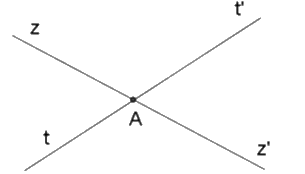
Vì hai đường thẳng $zz'$ và $tt'$ cắt nhau tại $A$ nên $Az'$ là tia đối của tia $Az,At'$ là tia đối của tia $At.$ Vậy góc đối đỉnh với \(\widehat {zAt'}\) là \(\widehat {z'At}\).
Cho góc \(xBy\) đối đỉnh với góc \(x'By'\) và \(\widehat {xBy} = 60^\circ \) . Tính số đo góc \(x'By'.\)
$30^\circ$
$120^\circ$
$90^\circ$
$60^\circ$
Đáp án : D
Áp dụng tính chất: Hai góc đối đỉnh thì bằng nhau.
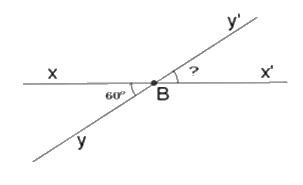
Vẽ \(\widehat {x'By'}\) là góc đối đỉnh với \(\widehat {xBy}\). Khi đó:
\(\widehat {x'By'} = \widehat {xBy} = {60^o}\) (tính chất hai góc đối đỉnh)
Cho hai đường thẳng \(xx'\) và \(yy'\) giao nhau tại \(O\) sao cho \(\widehat {xOy} = 45^\circ \) . Chọn câu sai.
$\widehat {x'Oy} = 135^\circ $
$\widehat {x'Oy'} = 45^\circ $
$\widehat {xOy'} = 135^\circ $
$\widehat {x'Oy'} = 135^\circ $
Đáp án : D
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
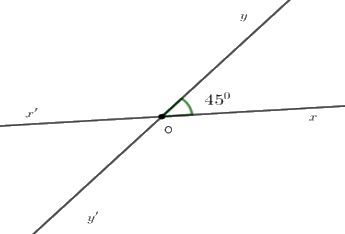
Vì hai đường thẳng $xx'$ và $yy'$ cắt nhau tại $O$ nên $Ox'$ là tia đối của tia $Ox;Oy'$ là tia đối của tia $Oy.$
Suy ra \(\widehat {xOy}\) và \(\widehat {x'Oy'}\) ; \(\widehat {x'Oy}\) và \(\widehat {xOy'}\) là hai cặp góc đối đỉnh.
Do đó \(\widehat {x'Oy'} = \widehat {xOy} = 45^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'}\)
Lại có \(\widehat {xOy}\) và \(\widehat {x'Oy}\) là hai góc ở vị trí kề bù nên \(\widehat {xOy} + \widehat {x'Oy} = 180^\circ \)\( \Rightarrow 45^\circ + \widehat {x'Oy} = 180^\circ \Rightarrow \widehat {x'Oy} = 180^\circ - 45^\circ \)
\( \Rightarrow \widehat {x'Oy} = 135^\circ \)
Vậy \(\widehat {x'Oy'} = \widehat {xOy} = 45^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'} = 135^\circ .\)
Suy ra A, B, C đúng, D sai.
Cho cặp góc đối đỉnh \(\widehat {tOz}\) và \(\widehat {t'Oz'}\) (\(Oz\) và $Oz'$ là hai tia đối nhau). Biết \(\widehat {tOz'} = 4.\widehat {tOz}\). Tính các góc \(\widehat {tOz}\) và \(\widehat {t'Oz'}.\)
\(\widehat {zOt} = \widehat {z'Ot'} = 72^\circ \)
\(\widehat {zOt} = \widehat {z'Ot'} = 30^\circ \)
\(\widehat {zOt} = \widehat {z'Ot'} = 36^\circ \)
\(\widehat {zOt} = 72^\circ ;\,\widehat {z'Ot'} = 36^\circ \)
Đáp án : C
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
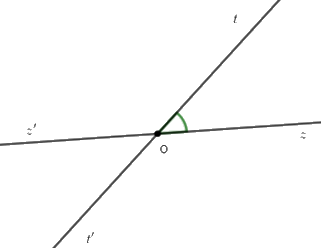
Ta có \(\widehat {zOt} + \widehat {tOz'} = 180^\circ \) (hai góc kề bù) mà \(\widehat {tOz'} = 4.\widehat {tOz}\) \( \Rightarrow \widehat {zOt} + 4.\widehat {zOt} = 180^\circ \) \( \Rightarrow 5.\widehat {zOt} = 180^\circ \Rightarrow \widehat {zOt} = 36^\circ \)
Vì \(\widehat {tOz}\) và \(\widehat {t'Oz'}\) là hai góc đối đỉnh nên \(\widehat {zOt} = \widehat {z'Ot'} = 36^\circ .\)
Vẽ góc $xOy$ có số đo bằng $35^\circ$. Vẽ góc $x'Oy'$ đối đỉnh với góc $xOy.$ Viết tên các góc có số đo bằng $145^o.$
\(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy'}\)
\(\widehat {xOy}\,\,;\,\,\widehat {x'Oy'}\)
\(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy}\)
\(\widehat {xOy'}\,\,;\,\,\widehat {xOy}\)
Đáp án : C
Áp dụng tính chất hai góc đối đỉnh, tính chất hai góc kề bù để tính các góc còn lại.
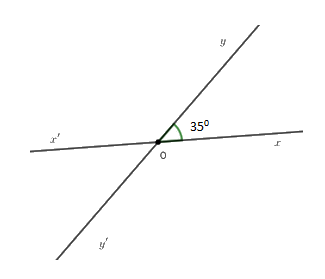
Vì hai đường thẳng $xx'$ và $yy'$ cắt nhau tại $O$ nên $Ox'$ là tia đối của tia $Ox;Oy'$ là tia đối của tia $Oy.$
Suy ra \(\widehat {xOy}\) và \(\widehat {x'Oy'}\) ; \(\widehat {x'Oy}\) và \(\widehat {xOy'}\) là hai cặp góc đối đỉnh.
Do đó \(\widehat {x'Oy'} = \widehat {xOy} = 35^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'}\)
Lại có \(\widehat {xOy}\) và \(\widehat {x'Oy}\) là hai góc ở vị trí kề bù nên \(\widehat {xOy} + \widehat {x'Oy} = 180^\circ \)\( \Rightarrow 35^\circ + \widehat {x'Oy} = 180^\circ \Rightarrow \widehat {x'Oy} = 180^\circ - 35^\circ \)
\( \Rightarrow \widehat {x'Oy} = 145^\circ \)
Vậy \(\widehat {x'Oy'} = \widehat {xOy} = 45^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'} = 145^\circ .\)
Hai góc có số đo bằng ${145^o}$ là : \(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy}\)
Hai đường thẳng \(AB\) và \(CD\) cắt nhau tại $O$ tạo thành \(\widehat {AOC} = 60^\circ \) . Gọi \(OM\) là phân giác \(\widehat {AOC}\) và \(ON\) là tia đối của tia \(OM\). Tính \(\widehat {BON}\) và \(\widehat {DON}.\)
\(\widehat {BON} = \widehat {DON} = 25^\circ \)
\(\widehat {BON} = \widehat {DON} = 30^\circ \)
\(\widehat {BON} = \widehat {DON} = 60^\circ \)
\(\widehat {BON} = \widehat {DON} = 45^\circ \)
Đáp án : B
+ Sử dụng tính chất tia phân giác tính các góc \(\widehat {AOM};\widehat {COM}\)
+ Sử dụng tính chất hai góc đối đỉnh để suy ra hai góc \(\widehat {BON}\) và \(\widehat {DON}.\)
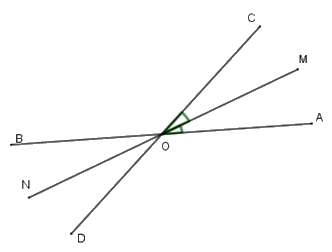
Vì \(AB\) và \(CD\) cắt nhau tại \(O\) nên \(OA\) và \(OB\) là hai tia đối nhau, \(OC\) và \(OD\) là hai tia đối nhau.
Vì \(OM\) là tia phân giác \(\widehat {COA}\) nên \(\widehat {AOM} = \widehat {COM} = \dfrac{{\widehat {COA}}}{2} = \dfrac{{60}}{2} = 30^\circ \)
Mà \(ON\) và \(OM\) là hai tia đối nhau nên \(\widehat {AOM}\) và \(\widehat {BON}\) là hai góc đối đỉnh; \(\widehat {COM}\) và \(\widehat {DON}\) là hai góc đối đỉnh
Suy ra \(\widehat {AOM} = \widehat {BON} = 30^\circ ;\widehat {COM} = \widehat {DON} = 30^\circ \) hay \(\widehat {BON} = \widehat {DON} = 30^\circ .\)
Hai đường thẳng $AB$ và $CD$ cắt nhau tại $O.$ Biết \(\widehat {AOC} - \widehat {AOD} = {50^0}.\) Chọn câu đúng.
\(\widehat {AOC} = 110^\circ \)
\(\widehat {BOC} = 65^\circ \)
\(\widehat {BOD} = 120^\circ \)
\(\widehat {AOD} = 50^\circ \)
Đáp án : B
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
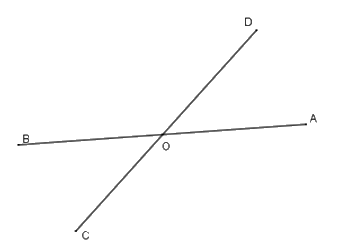
Vì \(\widehat {AOD}\) và \(\widehat {AOC}\) là hai góc kề bù nên \(\widehat {AOD} + \widehat {AOC} = 180^\circ \) mà \(\widehat {AOC} - \widehat {AOD} = 50^\circ \)
Nên \(\widehat {AOC} = \dfrac{{180^\circ + 50^\circ }}{2} = 115^\circ \) và \(\widehat {AOD} = 180^\circ - \widehat {AOC} = 65^\circ \)
Mà \(\widehat {AOD}\) và \(\widehat {BOC}\) là hai góc đối đỉnh nên \(\widehat {BOC} = \widehat {AOD} = 65^\circ .\)
Lại có \(\widehat {BOD}\) và \(\widehat {AOC}\) là hai góc đối đỉnh nên \(\widehat {BOD} = \widehat {AOC} = 115^\circ .\)
Vậy \(\widehat {BOD} = \widehat {AOC} = 115^\circ ;\,\widehat {BOC} = \widehat {AOD} = 65^\circ .\)
Hai đường thẳng zz’ và tt’ cắt nhau tại \(A\). Góc đối đỉnh với \(\widehat {zAt'}\) là:
\(\widehat {z'At'}\)
\(\widehat {z'At}\)
\(\widehat {zAt'}\)
\(\widehat {zAt}\)
Đáp án : B
Áp dụng định nghĩa hai góc đối đỉnh, xác định tia đối của tia Az và At, từ đó xác định góc đối đỉnh với \(\widehat {zAt}\).
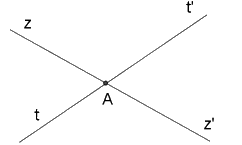
Vì hai đường thẳng \(zz'\) và \(tt'\) cắt nhau tại \(A\) nên \(Az'\) là tia đối của tia \(Az,At'\) là tia đối của tia \(At.\) Vậy góc đối đỉnh với \(\widehat {zAt'}\) là \(\widehat {z'At}\).
Cho hai đường thẳng \(xx'\) và \(yy'\) cắt nhau tại \(O\) sao cho \(\widehat {xOy} = 135^\circ \) . Chọn câu đúng:
\(\widehat {x'Oy} = 135^\circ \)
\(\widehat {x'Oy'} = 45^\circ \)
\(\widehat {xOy'} = 135^\circ \)
\(\widehat {x'Oy'} = 135^\circ \)
Đáp án : D
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
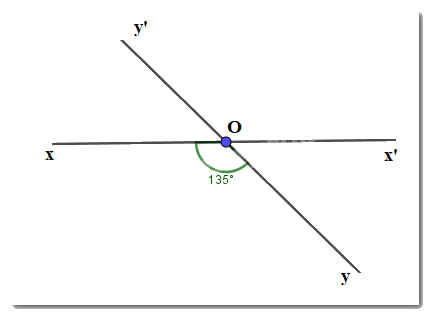
Vì hai đường thẳng \(xx'\) và \(yy'\) cắt nhau tại \(O\) nên \(Ox'\) là tia đối của tia \(Ox;Oy'\) là tia đối của tia \(Oy.\)
Suy ra \(\widehat {xOy}\) và \(\widehat {x'Oy'}\) ; \(\widehat {x'Oy}\) và \(\widehat {xOy'}\) là hai cặp góc đối đỉnh.
Do đó \(\widehat {x'Oy'} = \widehat {xOy} = 135^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'}\)
Lại có \(\widehat {xOy}\) và \(\widehat {x'Oy}\) là hai góc kề bù nên
\(\widehat {xOy} + \widehat {x'Oy} = 180^\circ \)
\(45^\circ + \widehat {x'Oy} = 180^\circ \)
Suy ra \(\widehat {x'Oy} = 180^\circ - 135^\circ = 45^\circ \)
Do đó \(\widehat {x'Oy} = \widehat {xOy'} = 45^\circ .\)
Vậy \(\widehat {x'Oy'} = \widehat {xOy} = 135^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'} = 45^\circ .\)
Cho 2 đường thẳng ab và cd cắt nhau tại M ( tia Ma đối tia Mb). Biết \(\widehat {aMc} = 5.\widehat {bMc}\). Tính số đo \(\widehat {aMc}\) ?
30\(^\circ \)
36\(^\circ \)
144\(^\circ \)
150\(^\circ \)
Đáp án : D
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
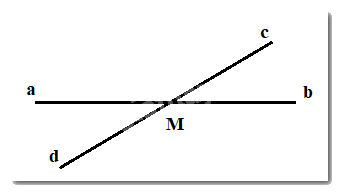
Ta có: \(\widehat {aMc} + \widehat {bMc} = 180^\circ \) ( 2 góc kề bù)
Mà \(\widehat {aMc} = 5.\widehat {bMc}\)
\(\begin{array}{l} 5.\widehat {bMc} + \widehat {bMc} = 180^\circ \\ 6.\widehat {bMc} = 180^\circ \\ \widehat {bMc} = 180^\circ :6 = 30^\circ \\ \widehat {aMc} = 5.30^\circ = 150^\circ \end{array}\)
\(\begin{array}{l} 5.\widehat {bMc} + \widehat {bMc} = 180^\circ \\ 6.\widehat {bMc} = 180^\circ \\ \widehat {bMc} = 180^\circ :6 = 30^\circ \\ \widehat {aMc} = 5.30^\circ = 150^\circ \end{array}\)
Cho \(\widehat {ABC} = {56^o}\). Vẽ \(\widehat {ABC'}\) kề bù với \(\widehat {ABC}\); \(\widehat {C'BA'}\) kề bù với \(\widehat {ABC'}\). Tính số đo \(\widehat {C'BA'}\).
124o
142o
65o
56o
Đáp án : D
Áp dụng tính chất hai góc kề bù, xác định các tia đối từ đó xác định góc đối đỉnh. Áp dụng tính chất hai góc đối đỉnh để tính góc \(C'BA'.\)
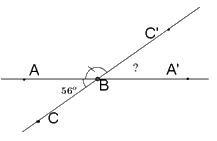
Vì góc \(ABC'\) kề bù với góc \(ABC\) nên \(BC'\) là tia đối của tia \(BC.\)
Vì góc \(C'BA'\) kề bù với góc \(ABC'\) nên \(BA'\) là tia đối của tia \(BA.\)
Do đó, góc \(C'BA'\) và góc \(ABC\) đối đỉnh.
\( \Rightarrow \widehat {C'BA'} = \widehat {ABC} = {56^o}\)
Vẽ góc \(xOy\) có số đo bằng 125o. Vẽ góc \(x'Oy'\) đối đỉnh với góc \(xOy.\) Viết tên các góc có số đo bằng 55o.
\(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy'}\)
\(\widehat {xOy}\,\,;\,\,\widehat {x'Oy'}\)
\(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy}\)
\(\widehat {xOy'}\,\,;\,\,\widehat {xOy}\)
Đáp án : C
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
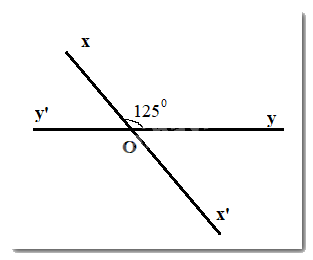
Vì hai đường thẳng \(xx'\) và \(yy'\) cắt nhau tại \(O\) nên \(Ox'\) là tia đối của tia \(Ox;Oy'\) là tia đối của tia \(Oy.\)
Suy ra \(\widehat {xOy}\) và \(\widehat {x'Oy'}\) ; \(\widehat {x'Oy}\) và \(\widehat {xOy'}\) là hai cặp góc đối đỉnh.
Do đó \(\widehat {x'Oy'} = \widehat {xOy} = 125^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'}\)
Lại có \(\widehat {xOy}\) và \(\widehat {x'Oy}\) là hai góc ở vị trí kề bù nên
\(\widehat {xOy} + \widehat {x'Oy} = 180^\circ \)
Suy ra \(125^\circ + \widehat {x'Oy} = 180^\circ \)
Suy ra \(\widehat {x'Oy} = 180^\circ - 125^\circ = 55^\circ \)
Hai góc có số đo bằng 55o là : \(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy}\)
Cho tia Ok là tia phân giác của \(\widehat {mOn}\)= 70o . Tính \(\widehat {nOk}\)
70o
140o
35o
110o
Đáp án : C
Sử dụng tính chất tia phân giác của một góc
Vì Ok là tia phân giác của \(\widehat {mOn}\) nên \(\widehat {mOk} = \widehat {nOk} = \frac{1}{2}.\widehat {mOn} = \frac{1}{2}.70^\circ = 35^\circ \)
Cho hình vẽ sau. Biết góc $xOy'$ đối đỉnh với góc $x'Oy,$ biết \(\widehat {xOy'} = {\widehat O_1} = {165^o}\). Tính các góc đỉnh O (khác góc bẹt).
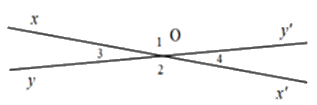
\({\widehat O_2} = {165^o};\,{\widehat O_3} = {15^o};\,\,{\widehat O_4} = {165^o}\,\,\)
\({\widehat O_2} = {165^o};\,{\widehat O_3} = {15^o};\,\,{\widehat O_4} = {15^o}\,\,\)
\({\widehat O_2} = {15^o};\,{\widehat O_3} = {15^o};\,\,{\widehat O_4} = {165^o}\,\,\)
\({\widehat O_2} = {15^o};\,{\widehat O_3} = {165^o};\,\,{\widehat O_4} = {15^o}\,\,\)
Đáp án : B
Áp dụng tính chất hai góc đối đỉnh, hai góc kề bù để tính các góc còn lại.
\({\widehat O_2} = {\widehat O_1} = {165^o}\) (tính chất hai góc đối đỉnh)
Góc ${O_1}$ và góc ${O_4}$ là hai góc kề bù
\( \Rightarrow {\widehat O_1} + {\widehat O_4} = {180^o}\)
\( \Rightarrow {\widehat O_4} = {180^o} - {\widehat O_1}\)
\( \Rightarrow {\widehat O_4} = {180^o} - {165^o} = {15^o}\)
\({\widehat O_3} = {\widehat O_4} = {15^o}\,\) (hai góc đối đỉnh)
Hai đường thẳng zz’ và tt’ cắt nhau tại $A$. Góc đối đỉnh với \(\widehat {zAt'}\) là:
\(\widehat {z'At'}\)
\(\widehat {z'At}\)
\(\widehat {zAt'}\) \(\)
\(\widehat {zAt}\)
Cho góc \(xBy\) đối đỉnh với góc \(x'By'\) và \(\widehat {xBy} = 60^\circ \) . Tính số đo góc \(x'By'.\)
$30^\circ$
$120^\circ$
$90^\circ$
$60^\circ$
Cho hai đường thẳng \(xx'\) và \(yy'\) giao nhau tại \(O\) sao cho \(\widehat {xOy} = 45^\circ \) . Chọn câu sai.
$\widehat {x'Oy} = 135^\circ $
$\widehat {x'Oy'} = 45^\circ $
$\widehat {xOy'} = 135^\circ $
$\widehat {x'Oy'} = 135^\circ $
Cho cặp góc đối đỉnh \(\widehat {tOz}\) và \(\widehat {t'Oz'}\) (\(Oz\) và $Oz'$ là hai tia đối nhau). Biết \(\widehat {tOz'} = 4.\widehat {tOz}\). Tính các góc \(\widehat {tOz}\) và \(\widehat {t'Oz'}.\)
\(\widehat {zOt} = \widehat {z'Ot'} = 72^\circ \)
\(\widehat {zOt} = \widehat {z'Ot'} = 30^\circ \)
\(\widehat {zOt} = \widehat {z'Ot'} = 36^\circ \)
\(\widehat {zOt} = 72^\circ ;\,\widehat {z'Ot'} = 36^\circ \)
Vẽ góc $xOy$ có số đo bằng $35^\circ$. Vẽ góc $x'Oy'$ đối đỉnh với góc $xOy.$ Viết tên các góc có số đo bằng $145^o.$
\(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy'}\)
\(\widehat {xOy}\,\,;\,\,\widehat {x'Oy'}\)
\(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy}\)
\(\widehat {xOy'}\,\,;\,\,\widehat {xOy}\)
Hai đường thẳng \(AB\) và \(CD\) cắt nhau tại $O$ tạo thành \(\widehat {AOC} = 60^\circ \) . Gọi \(OM\) là phân giác \(\widehat {AOC}\) và \(ON\) là tia đối của tia \(OM\). Tính \(\widehat {BON}\) và \(\widehat {DON}.\)
\(\widehat {BON} = \widehat {DON} = 25^\circ \)
\(\widehat {BON} = \widehat {DON} = 30^\circ \)
\(\widehat {BON} = \widehat {DON} = 60^\circ \)
\(\widehat {BON} = \widehat {DON} = 45^\circ \)
Hai đường thẳng $AB$ và $CD$ cắt nhau tại $O.$ Biết \(\widehat {AOC} - \widehat {AOD} = {50^0}.\) Chọn câu đúng.
\(\widehat {AOC} = 110^\circ \)
\(\widehat {BOC} = 65^\circ \)
\(\widehat {BOD} = 120^\circ \)
\(\widehat {AOD} = 50^\circ \)
Hai đường thẳng zz’ và tt’ cắt nhau tại \(A\). Góc đối đỉnh với \(\widehat {zAt'}\) là:
\(\widehat {z'At'}\)
\(\widehat {z'At}\)
\(\widehat {zAt'}\)
\(\widehat {zAt}\)
Cho hai đường thẳng \(xx'\) và \(yy'\) cắt nhau tại \(O\) sao cho \(\widehat {xOy} = 135^\circ \) . Chọn câu đúng:
\(\widehat {x'Oy} = 135^\circ \)
\(\widehat {x'Oy'} = 45^\circ \)
\(\widehat {xOy'} = 135^\circ \)
\(\widehat {x'Oy'} = 135^\circ \)
Cho 2 đường thẳng ab và cd cắt nhau tại M ( tia Ma đối tia Mb). Biết \(\widehat {aMc} = 5.\widehat {bMc}\). Tính số đo \(\widehat {aMc}\) ?
30\(^\circ \)
36\(^\circ \)
144\(^\circ \)
150\(^\circ \)
Cho \(\widehat {ABC} = {56^o}\). Vẽ \(\widehat {ABC'}\) kề bù với \(\widehat {ABC}\); \(\widehat {C'BA'}\) kề bù với \(\widehat {ABC'}\). Tính số đo \(\widehat {C'BA'}\).
124o
142o
65o
56o
Vẽ góc \(xOy\) có số đo bằng 125o. Vẽ góc \(x'Oy'\) đối đỉnh với góc \(xOy.\) Viết tên các góc có số đo bằng 55o.
\(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy'}\)
\(\widehat {xOy}\,\,;\,\,\widehat {x'Oy'}\)
\(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy}\)
\(\widehat {xOy'}\,\,;\,\,\widehat {xOy}\)
Cho tia Ok là tia phân giác của \(\widehat {mOn}\)= 70o . Tính \(\widehat {nOk}\)
70o
140o
35o
110o
Cho hình vẽ sau. Biết góc $xOy'$ đối đỉnh với góc $x'Oy,$ biết \(\widehat {xOy'} = {\widehat O_1} = {165^o}\). Tính các góc đỉnh O (khác góc bẹt).

\({\widehat O_2} = {165^o};\,{\widehat O_3} = {15^o};\,\,{\widehat O_4} = {165^o}\,\,\)
\({\widehat O_2} = {165^o};\,{\widehat O_3} = {15^o};\,\,{\widehat O_4} = {15^o}\,\,\)
\({\widehat O_2} = {15^o};\,{\widehat O_3} = {15^o};\,\,{\widehat O_4} = {165^o}\,\,\)
\({\widehat O_2} = {15^o};\,{\widehat O_3} = {165^o};\,\,{\widehat O_4} = {15^o}\,\,\)
Hai đường thẳng zz’ và tt’ cắt nhau tại $A$. Góc đối đỉnh với \(\widehat {zAt'}\) là:
\(\widehat {z'At'}\)
\(\widehat {z'At}\)
\(\widehat {zAt'}\) \(\)
\(\widehat {zAt}\)
Đáp án : B
Áp dụng định nghĩa hai góc đối đỉnh, xác định tia đối của tia \(Az\) và \(At'\), từ đó xác định góc đối đỉnh với \(\widehat {zAt'}\).

Vì hai đường thẳng $zz'$ và $tt'$ cắt nhau tại $A$ nên $Az'$ là tia đối của tia $Az,At'$ là tia đối của tia $At.$ Vậy góc đối đỉnh với \(\widehat {zAt'}\) là \(\widehat {z'At}\).
Cho góc \(xBy\) đối đỉnh với góc \(x'By'\) và \(\widehat {xBy} = 60^\circ \) . Tính số đo góc \(x'By'.\)
$30^\circ$
$120^\circ$
$90^\circ$
$60^\circ$
Đáp án : D
Áp dụng tính chất: Hai góc đối đỉnh thì bằng nhau.

Vẽ \(\widehat {x'By'}\) là góc đối đỉnh với \(\widehat {xBy}\). Khi đó:
\(\widehat {x'By'} = \widehat {xBy} = {60^o}\) (tính chất hai góc đối đỉnh)
Cho hai đường thẳng \(xx'\) và \(yy'\) giao nhau tại \(O\) sao cho \(\widehat {xOy} = 45^\circ \) . Chọn câu sai.
$\widehat {x'Oy} = 135^\circ $
$\widehat {x'Oy'} = 45^\circ $
$\widehat {xOy'} = 135^\circ $
$\widehat {x'Oy'} = 135^\circ $
Đáp án : D
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)

Vì hai đường thẳng $xx'$ và $yy'$ cắt nhau tại $O$ nên $Ox'$ là tia đối của tia $Ox;Oy'$ là tia đối của tia $Oy.$
Suy ra \(\widehat {xOy}\) và \(\widehat {x'Oy'}\) ; \(\widehat {x'Oy}\) và \(\widehat {xOy'}\) là hai cặp góc đối đỉnh.
Do đó \(\widehat {x'Oy'} = \widehat {xOy} = 45^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'}\)
Lại có \(\widehat {xOy}\) và \(\widehat {x'Oy}\) là hai góc ở vị trí kề bù nên \(\widehat {xOy} + \widehat {x'Oy} = 180^\circ \)\( \Rightarrow 45^\circ + \widehat {x'Oy} = 180^\circ \Rightarrow \widehat {x'Oy} = 180^\circ - 45^\circ \)
\( \Rightarrow \widehat {x'Oy} = 135^\circ \)
Vậy \(\widehat {x'Oy'} = \widehat {xOy} = 45^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'} = 135^\circ .\)
Suy ra A, B, C đúng, D sai.
Cho cặp góc đối đỉnh \(\widehat {tOz}\) và \(\widehat {t'Oz'}\) (\(Oz\) và $Oz'$ là hai tia đối nhau). Biết \(\widehat {tOz'} = 4.\widehat {tOz}\). Tính các góc \(\widehat {tOz}\) và \(\widehat {t'Oz'}.\)
\(\widehat {zOt} = \widehat {z'Ot'} = 72^\circ \)
\(\widehat {zOt} = \widehat {z'Ot'} = 30^\circ \)
\(\widehat {zOt} = \widehat {z'Ot'} = 36^\circ \)
\(\widehat {zOt} = 72^\circ ;\,\widehat {z'Ot'} = 36^\circ \)
Đáp án : C
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau

Ta có \(\widehat {zOt} + \widehat {tOz'} = 180^\circ \) (hai góc kề bù) mà \(\widehat {tOz'} = 4.\widehat {tOz}\) \( \Rightarrow \widehat {zOt} + 4.\widehat {zOt} = 180^\circ \) \( \Rightarrow 5.\widehat {zOt} = 180^\circ \Rightarrow \widehat {zOt} = 36^\circ \)
Vì \(\widehat {tOz}\) và \(\widehat {t'Oz'}\) là hai góc đối đỉnh nên \(\widehat {zOt} = \widehat {z'Ot'} = 36^\circ .\)
Vẽ góc $xOy$ có số đo bằng $35^\circ$. Vẽ góc $x'Oy'$ đối đỉnh với góc $xOy.$ Viết tên các góc có số đo bằng $145^o.$
\(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy'}\)
\(\widehat {xOy}\,\,;\,\,\widehat {x'Oy'}\)
\(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy}\)
\(\widehat {xOy'}\,\,;\,\,\widehat {xOy}\)
Đáp án : C
Áp dụng tính chất hai góc đối đỉnh, tính chất hai góc kề bù để tính các góc còn lại.

Vì hai đường thẳng $xx'$ và $yy'$ cắt nhau tại $O$ nên $Ox'$ là tia đối của tia $Ox;Oy'$ là tia đối của tia $Oy.$
Suy ra \(\widehat {xOy}\) và \(\widehat {x'Oy'}\) ; \(\widehat {x'Oy}\) và \(\widehat {xOy'}\) là hai cặp góc đối đỉnh.
Do đó \(\widehat {x'Oy'} = \widehat {xOy} = 35^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'}\)
Lại có \(\widehat {xOy}\) và \(\widehat {x'Oy}\) là hai góc ở vị trí kề bù nên \(\widehat {xOy} + \widehat {x'Oy} = 180^\circ \)\( \Rightarrow 35^\circ + \widehat {x'Oy} = 180^\circ \Rightarrow \widehat {x'Oy} = 180^\circ - 35^\circ \)
\( \Rightarrow \widehat {x'Oy} = 145^\circ \)
Vậy \(\widehat {x'Oy'} = \widehat {xOy} = 45^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'} = 145^\circ .\)
Hai góc có số đo bằng ${145^o}$ là : \(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy}\)
Hai đường thẳng \(AB\) và \(CD\) cắt nhau tại $O$ tạo thành \(\widehat {AOC} = 60^\circ \) . Gọi \(OM\) là phân giác \(\widehat {AOC}\) và \(ON\) là tia đối của tia \(OM\). Tính \(\widehat {BON}\) và \(\widehat {DON}.\)
\(\widehat {BON} = \widehat {DON} = 25^\circ \)
\(\widehat {BON} = \widehat {DON} = 30^\circ \)
\(\widehat {BON} = \widehat {DON} = 60^\circ \)
\(\widehat {BON} = \widehat {DON} = 45^\circ \)
Đáp án : B
+ Sử dụng tính chất tia phân giác tính các góc \(\widehat {AOM};\widehat {COM}\)
+ Sử dụng tính chất hai góc đối đỉnh để suy ra hai góc \(\widehat {BON}\) và \(\widehat {DON}.\)

Vì \(AB\) và \(CD\) cắt nhau tại \(O\) nên \(OA\) và \(OB\) là hai tia đối nhau, \(OC\) và \(OD\) là hai tia đối nhau.
Vì \(OM\) là tia phân giác \(\widehat {COA}\) nên \(\widehat {AOM} = \widehat {COM} = \dfrac{{\widehat {COA}}}{2} = \dfrac{{60}}{2} = 30^\circ \)
Mà \(ON\) và \(OM\) là hai tia đối nhau nên \(\widehat {AOM}\) và \(\widehat {BON}\) là hai góc đối đỉnh; \(\widehat {COM}\) và \(\widehat {DON}\) là hai góc đối đỉnh
Suy ra \(\widehat {AOM} = \widehat {BON} = 30^\circ ;\widehat {COM} = \widehat {DON} = 30^\circ \) hay \(\widehat {BON} = \widehat {DON} = 30^\circ .\)
Hai đường thẳng $AB$ và $CD$ cắt nhau tại $O.$ Biết \(\widehat {AOC} - \widehat {AOD} = {50^0}.\) Chọn câu đúng.
\(\widehat {AOC} = 110^\circ \)
\(\widehat {BOC} = 65^\circ \)
\(\widehat {BOD} = 120^\circ \)
\(\widehat {AOD} = 50^\circ \)
Đáp án : B
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau

Vì \(\widehat {AOD}\) và \(\widehat {AOC}\) là hai góc kề bù nên \(\widehat {AOD} + \widehat {AOC} = 180^\circ \) mà \(\widehat {AOC} - \widehat {AOD} = 50^\circ \)
Nên \(\widehat {AOC} = \dfrac{{180^\circ + 50^\circ }}{2} = 115^\circ \) và \(\widehat {AOD} = 180^\circ - \widehat {AOC} = 65^\circ \)
Mà \(\widehat {AOD}\) và \(\widehat {BOC}\) là hai góc đối đỉnh nên \(\widehat {BOC} = \widehat {AOD} = 65^\circ .\)
Lại có \(\widehat {BOD}\) và \(\widehat {AOC}\) là hai góc đối đỉnh nên \(\widehat {BOD} = \widehat {AOC} = 115^\circ .\)
Vậy \(\widehat {BOD} = \widehat {AOC} = 115^\circ ;\,\widehat {BOC} = \widehat {AOD} = 65^\circ .\)
Hai đường thẳng zz’ và tt’ cắt nhau tại \(A\). Góc đối đỉnh với \(\widehat {zAt'}\) là:
\(\widehat {z'At'}\)
\(\widehat {z'At}\)
\(\widehat {zAt'}\)
\(\widehat {zAt}\)
Đáp án : B
Áp dụng định nghĩa hai góc đối đỉnh, xác định tia đối của tia Az và At, từ đó xác định góc đối đỉnh với \(\widehat {zAt}\).

Vì hai đường thẳng \(zz'\) và \(tt'\) cắt nhau tại \(A\) nên \(Az'\) là tia đối của tia \(Az,At'\) là tia đối của tia \(At.\) Vậy góc đối đỉnh với \(\widehat {zAt'}\) là \(\widehat {z'At}\).
Cho hai đường thẳng \(xx'\) và \(yy'\) cắt nhau tại \(O\) sao cho \(\widehat {xOy} = 135^\circ \) . Chọn câu đúng:
\(\widehat {x'Oy} = 135^\circ \)
\(\widehat {x'Oy'} = 45^\circ \)
\(\widehat {xOy'} = 135^\circ \)
\(\widehat {x'Oy'} = 135^\circ \)
Đáp án : D
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)

Vì hai đường thẳng \(xx'\) và \(yy'\) cắt nhau tại \(O\) nên \(Ox'\) là tia đối của tia \(Ox;Oy'\) là tia đối của tia \(Oy.\)
Suy ra \(\widehat {xOy}\) và \(\widehat {x'Oy'}\) ; \(\widehat {x'Oy}\) và \(\widehat {xOy'}\) là hai cặp góc đối đỉnh.
Do đó \(\widehat {x'Oy'} = \widehat {xOy} = 135^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'}\)
Lại có \(\widehat {xOy}\) và \(\widehat {x'Oy}\) là hai góc kề bù nên
\(\widehat {xOy} + \widehat {x'Oy} = 180^\circ \)
\(45^\circ + \widehat {x'Oy} = 180^\circ \)
Suy ra \(\widehat {x'Oy} = 180^\circ - 135^\circ = 45^\circ \)
Do đó \(\widehat {x'Oy} = \widehat {xOy'} = 45^\circ .\)
Vậy \(\widehat {x'Oy'} = \widehat {xOy} = 135^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'} = 45^\circ .\)
Cho 2 đường thẳng ab và cd cắt nhau tại M ( tia Ma đối tia Mb). Biết \(\widehat {aMc} = 5.\widehat {bMc}\). Tính số đo \(\widehat {aMc}\) ?
30\(^\circ \)
36\(^\circ \)
144\(^\circ \)
150\(^\circ \)
Đáp án : D
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)

Ta có: \(\widehat {aMc} + \widehat {bMc} = 180^\circ \) ( 2 góc kề bù)
Mà \(\widehat {aMc} = 5.\widehat {bMc}\)
\(\begin{array}{l} 5.\widehat {bMc} + \widehat {bMc} = 180^\circ \\ 6.\widehat {bMc} = 180^\circ \\ \widehat {bMc} = 180^\circ :6 = 30^\circ \\ \widehat {aMc} = 5.30^\circ = 150^\circ \end{array}\)
\(\begin{array}{l} 5.\widehat {bMc} + \widehat {bMc} = 180^\circ \\ 6.\widehat {bMc} = 180^\circ \\ \widehat {bMc} = 180^\circ :6 = 30^\circ \\ \widehat {aMc} = 5.30^\circ = 150^\circ \end{array}\)
Cho \(\widehat {ABC} = {56^o}\). Vẽ \(\widehat {ABC'}\) kề bù với \(\widehat {ABC}\); \(\widehat {C'BA'}\) kề bù với \(\widehat {ABC'}\). Tính số đo \(\widehat {C'BA'}\).
124o
142o
65o
56o
Đáp án : D
Áp dụng tính chất hai góc kề bù, xác định các tia đối từ đó xác định góc đối đỉnh. Áp dụng tính chất hai góc đối đỉnh để tính góc \(C'BA'.\)

Vì góc \(ABC'\) kề bù với góc \(ABC\) nên \(BC'\) là tia đối của tia \(BC.\)
Vì góc \(C'BA'\) kề bù với góc \(ABC'\) nên \(BA'\) là tia đối của tia \(BA.\)
Do đó, góc \(C'BA'\) và góc \(ABC\) đối đỉnh.
\( \Rightarrow \widehat {C'BA'} = \widehat {ABC} = {56^o}\)
Vẽ góc \(xOy\) có số đo bằng 125o. Vẽ góc \(x'Oy'\) đối đỉnh với góc \(xOy.\) Viết tên các góc có số đo bằng 55o.
\(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy'}\)
\(\widehat {xOy}\,\,;\,\,\widehat {x'Oy'}\)
\(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy}\)
\(\widehat {xOy'}\,\,;\,\,\widehat {xOy}\)
Đáp án : C
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau

Vì hai đường thẳng \(xx'\) và \(yy'\) cắt nhau tại \(O\) nên \(Ox'\) là tia đối của tia \(Ox;Oy'\) là tia đối của tia \(Oy.\)
Suy ra \(\widehat {xOy}\) và \(\widehat {x'Oy'}\) ; \(\widehat {x'Oy}\) và \(\widehat {xOy'}\) là hai cặp góc đối đỉnh.
Do đó \(\widehat {x'Oy'} = \widehat {xOy} = 125^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'}\)
Lại có \(\widehat {xOy}\) và \(\widehat {x'Oy}\) là hai góc ở vị trí kề bù nên
\(\widehat {xOy} + \widehat {x'Oy} = 180^\circ \)
Suy ra \(125^\circ + \widehat {x'Oy} = 180^\circ \)
Suy ra \(\widehat {x'Oy} = 180^\circ - 125^\circ = 55^\circ \)
Hai góc có số đo bằng 55o là : \(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy}\)
Cho tia Ok là tia phân giác của \(\widehat {mOn}\)= 70o . Tính \(\widehat {nOk}\)
70o
140o
35o
110o
Đáp án : C
Sử dụng tính chất tia phân giác của một góc
Vì Ok là tia phân giác của \(\widehat {mOn}\) nên \(\widehat {mOk} = \widehat {nOk} = \frac{1}{2}.\widehat {mOn} = \frac{1}{2}.70^\circ = 35^\circ \)
Cho hình vẽ sau. Biết góc $xOy'$ đối đỉnh với góc $x'Oy,$ biết \(\widehat {xOy'} = {\widehat O_1} = {165^o}\). Tính các góc đỉnh O (khác góc bẹt).

\({\widehat O_2} = {165^o};\,{\widehat O_3} = {15^o};\,\,{\widehat O_4} = {165^o}\,\,\)
\({\widehat O_2} = {165^o};\,{\widehat O_3} = {15^o};\,\,{\widehat O_4} = {15^o}\,\,\)
\({\widehat O_2} = {15^o};\,{\widehat O_3} = {15^o};\,\,{\widehat O_4} = {165^o}\,\,\)
\({\widehat O_2} = {15^o};\,{\widehat O_3} = {165^o};\,\,{\widehat O_4} = {15^o}\,\,\)
Đáp án : B
Áp dụng tính chất hai góc đối đỉnh, hai góc kề bù để tính các góc còn lại.
\({\widehat O_2} = {\widehat O_1} = {165^o}\) (tính chất hai góc đối đỉnh)
Góc ${O_1}$ và góc ${O_4}$ là hai góc kề bù
\( \Rightarrow {\widehat O_1} + {\widehat O_4} = {180^o}\)
\( \Rightarrow {\widehat O_4} = {180^o} - {\widehat O_1}\)
\( \Rightarrow {\widehat O_4} = {180^o} - {165^o} = {15^o}\)
\({\widehat O_3} = {\widehat O_4} = {15^o}\,\) (hai góc đối đỉnh)
Bài 1 trong chương trình Toán 7 Cánh diều tập trung vào việc giới thiệu các khái niệm cơ bản về góc, các loại góc đặc biệt (góc nhọn, góc vuông, góc tù, góc bẹt) và mối quan hệ giữa chúng. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các bài học tiếp theo trong chương trình.
Câu hỏi: Cho góc AOB có số đo bằng 60°. Góc đối của góc AOB có số đo bằng bao nhiêu?
Giải: Góc đối của góc AOB là góc có tia đối của tia OA và tia đối của tia OB. Vì góc AOB có số đo bằng 60°, nên góc đối của góc AOB cũng có số đo bằng 60°.
Để củng cố kiến thức và nâng cao kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập trắc nghiệm khác trên giaitoan.edu.vn. Chúng tôi luôn cập nhật những đề thi mới nhất và chất lượng nhất để phục vụ nhu cầu học tập của các em.
Việc luyện tập thường xuyên là yếu tố then chốt để nắm vững kiến thức và đạt kết quả tốt trong các kỳ thi. Hãy dành thời gian ôn tập và làm bài tập trắc nghiệm một cách nghiêm túc để chuẩn bị tốt nhất cho các bài kiểm tra sắp tới.
Hy vọng rằng bài viết này đã cung cấp cho các em những kiến thức hữu ích về Trắc nghiệm Bài 1: Góc ở vị trí đặc biệt Toán 7 Cánh diều. Chúc các em học tập tốt và đạt được những thành công trong học tập!