Chủ đề 9 Ôn hè Toán 6 tập trung vào việc làm quen với khái niệm đối xứng trong hình học. Việc nắm vững kiến thức về trục đối xứng và tâm đối xứng là bước đệm quan trọng cho các bài học nâng cao hơn.
Giaitoan.edu.vn cung cấp bài giảng chi tiết, bài tập thực hành đa dạng, giúp học sinh hiểu rõ bản chất và áp dụng thành thạo kiến thức về dạng 3 này.
1. Trục đối xứng: Hình có một đường thẳng d chia hình thành hai phần mà khi ta “gấp” hình theo đường thẳng d thì hai phần đó “chồng khít” lên nhau là hình có trục đối xứng và đường thẳng d là trục đối xứng của nó.
1. Trục đối xứng:
Hình có một đường thẳng d chia hình thành hai phần mà khi ta “gấp” hình theo đường thẳng d thì hai phần đó “chồng khít” lên nhau là hình có trục đối xứng và đường thẳng d là trục đối xứng của nó.
Một số hình có trục đối xứng:
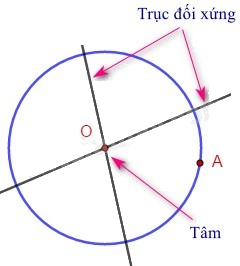
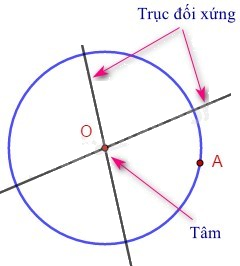
- Đường tròn: Mỗi đường thẳng đi qua tâm là một trục đối xứng.
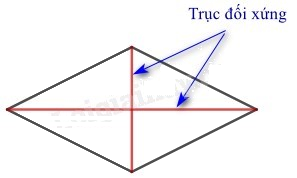
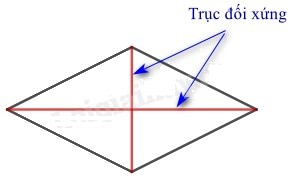
- Hình thoi: Mỗi đường chéo là một trục đối xứng.
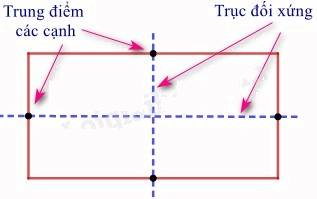
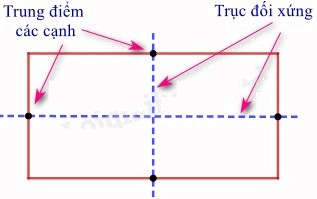
- Hình chữ nhật: Mỗi đường thẳng đi qua trung điểm hai cạnh đối diện là một trục đối xứng của hình chữ nhật.
2. Tâm đối xứng:
Những hình có một điểm O sao cho khi quay nửa vòng quanh điểm O ta được vị trí mới của hình chồng khít với vị trí ban đầu (trước khi quay) thì được gọi là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình.
Tâm đối xứng của một số hình phẳng
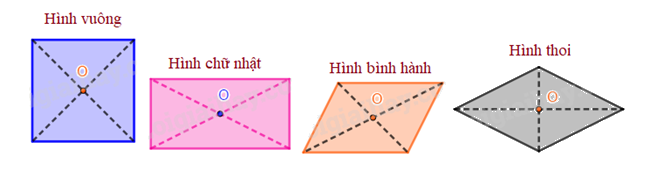
Tâm đối xứng của hình bình hành, hình thoi, hình vuông, hình chữ nhật là giao điểm của hai đường chéo.
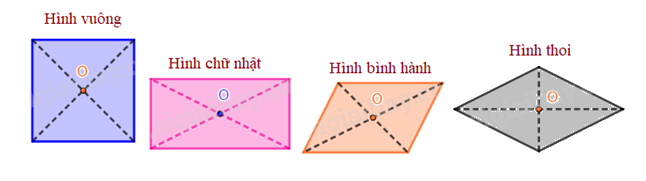
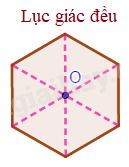
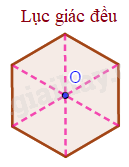
Tâm đối xứng của hình lục giác đều là giao điểm của các đường chéo chính.
Bài 1:
Hình dưới là đường gấp khúc có độ dài bằng \(4\) đơn vị.

Em hãy vẽ thêm vào hình đó:
a) Một đường gấp khúc có độ dài bằng 4 đơn vị để được một hình có đúng 1 trục đối xứng.
b) Một đường gấp khúc có độ dài bằng 4 đơn vị để được một hình có đúng 2 trục đối xứng.
c) Một đường gấp khúc có độ dài bằng 8 đơn vị để được một hình có đúng 4 trục đối xứng.
Bài 2:
Em hãy vẽ thêm vào mỗi hình dưới đây để được các hình có trục d là trục đối xứng.
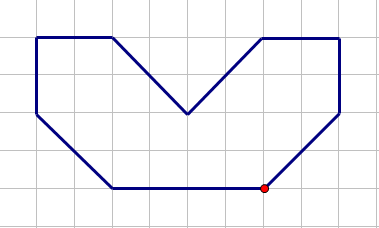
Bài 3:
Vẽ thêm để được hình có tâm đối xứng là điểm cho sẵn.
Lời giải chi tiết:
Bài 1:
Hình dưới là đường gấp khúc có độ dài bằng \(4\) đơn vị.

Em hãy vẽ thêm vào hình đó:
a) Một đường gấp khúc có độ dài bằng \(4\) đơn vị để được một hình có đúng \(1\) trục đối xứng.
b) Một đường gấp khúc có độ dài bằng \(4\) đơn vị để được một hình có đúng \(2\)trục đối xứng.
c) Một đường gấp khúc có độ dài bằng \(8\) đơn vị để được một hình có đúng \(4\) trục đối xứng.
Phương pháp
Vẽ đúng độ dài cạnh mà đề bài yêu cầu sao cho được hình mới có trục đối xứng.
Lời giải
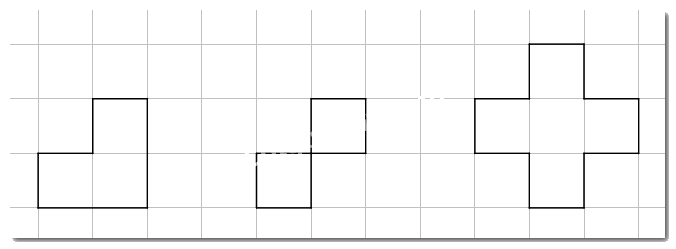
Bài 2:
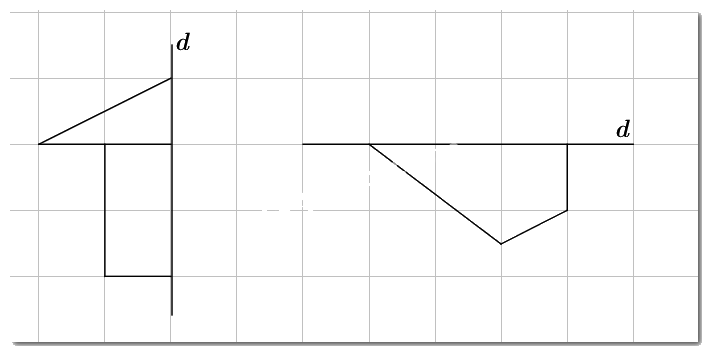
Em hãy vẽ thêm vào mỗi hình dưới đây để được các hình có trục \(d\) là trục đối xứng.
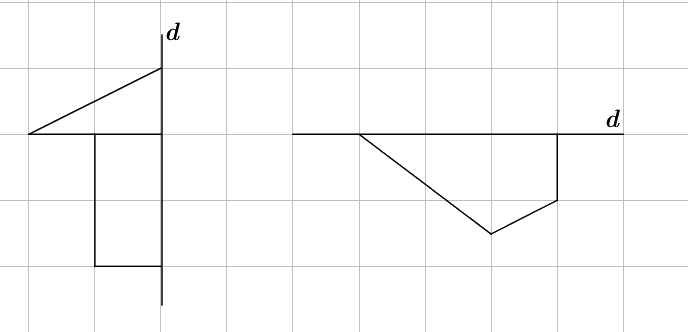
Phương pháp
Qua đường thẳng \(d\) ta vẽ hình đối xứng với hình đã cho.
Lời giải
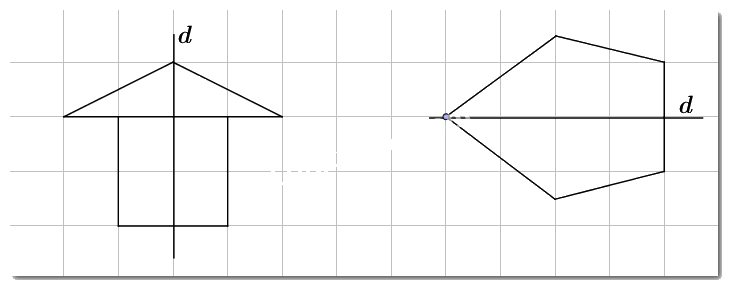
Bài 3:
Vẽ thêm để được hình có tâm đối xứng là điểm cho sẵn.
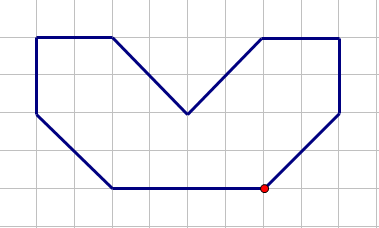
Phương pháp
Sử dụng lý thuyết tâm đối xứng của một hình.
Lời giải
Hình sau khi được vẽ thêm có điểm chỉ ra trên hình vẽ là tâm đối xứng:
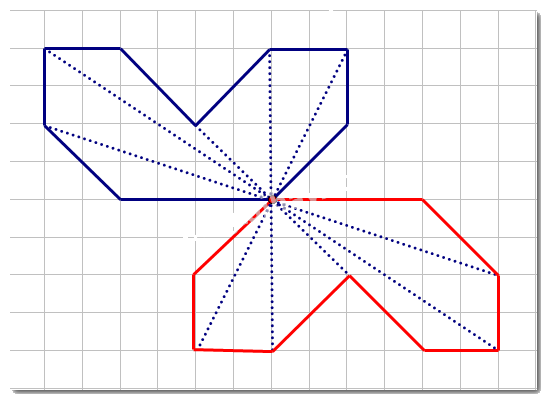
1. Trục đối xứng:
Hình có một đường thẳng d chia hình thành hai phần mà khi ta “gấp” hình theo đường thẳng d thì hai phần đó “chồng khít” lên nhau là hình có trục đối xứng và đường thẳng d là trục đối xứng của nó.
Một số hình có trục đối xứng:
- Đường tròn: Mỗi đường thẳng đi qua tâm là một trục đối xứng.
- Hình thoi: Mỗi đường chéo là một trục đối xứng.
- Hình chữ nhật: Mỗi đường thẳng đi qua trung điểm hai cạnh đối diện là một trục đối xứng của hình chữ nhật.
2. Tâm đối xứng:
Những hình có một điểm O sao cho khi quay nửa vòng quanh điểm O ta được vị trí mới của hình chồng khít với vị trí ban đầu (trước khi quay) thì được gọi là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình.
Tâm đối xứng của một số hình phẳng
Tâm đối xứng của hình bình hành, hình thoi, hình vuông, hình chữ nhật là giao điểm của hai đường chéo.
Tâm đối xứng của hình lục giác đều là giao điểm của các đường chéo chính.
Bài 1:
Hình dưới là đường gấp khúc có độ dài bằng \(4\) đơn vị.

Em hãy vẽ thêm vào hình đó:
a) Một đường gấp khúc có độ dài bằng 4 đơn vị để được một hình có đúng 1 trục đối xứng.
b) Một đường gấp khúc có độ dài bằng 4 đơn vị để được một hình có đúng 2 trục đối xứng.
c) Một đường gấp khúc có độ dài bằng 8 đơn vị để được một hình có đúng 4 trục đối xứng.
Bài 2:
Em hãy vẽ thêm vào mỗi hình dưới đây để được các hình có trục d là trục đối xứng.
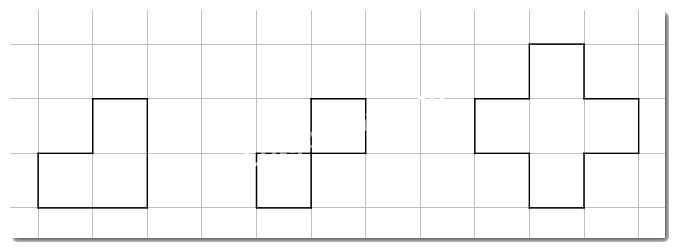
Bài 3:
Vẽ thêm để được hình có tâm đối xứng là điểm cho sẵn.

Lời giải chi tiết:
Bài 1:
Hình dưới là đường gấp khúc có độ dài bằng \(4\) đơn vị.

Em hãy vẽ thêm vào hình đó:
a) Một đường gấp khúc có độ dài bằng \(4\) đơn vị để được một hình có đúng \(1\) trục đối xứng.
b) Một đường gấp khúc có độ dài bằng \(4\) đơn vị để được một hình có đúng \(2\)trục đối xứng.
c) Một đường gấp khúc có độ dài bằng \(8\) đơn vị để được một hình có đúng \(4\) trục đối xứng.
Phương pháp
Vẽ đúng độ dài cạnh mà đề bài yêu cầu sao cho được hình mới có trục đối xứng.
Lời giải
Bài 2:
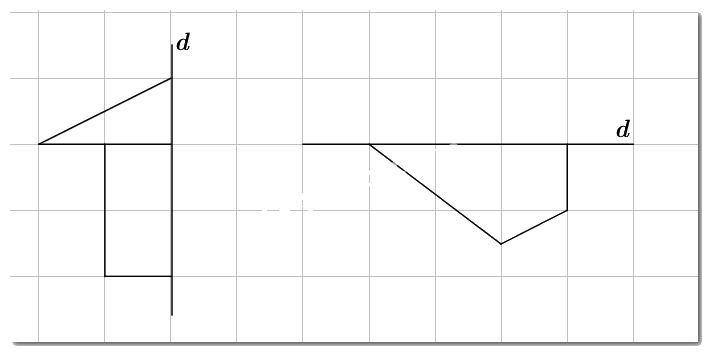
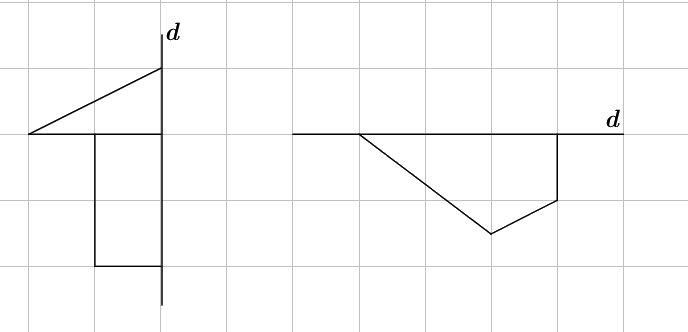
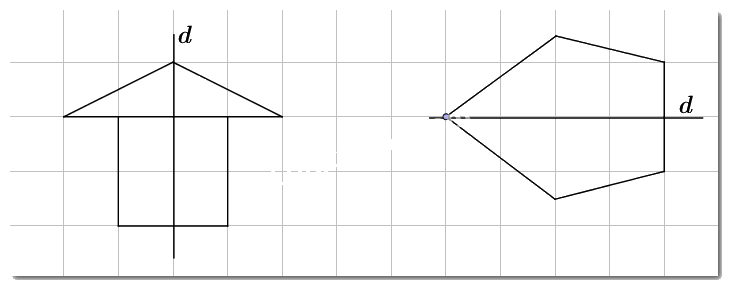
Em hãy vẽ thêm vào mỗi hình dưới đây để được các hình có trục \(d\) là trục đối xứng.
Phương pháp
Qua đường thẳng \(d\) ta vẽ hình đối xứng với hình đã cho.
Lời giải
Bài 3:
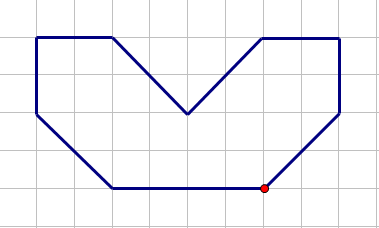
Vẽ thêm để được hình có tâm đối xứng là điểm cho sẵn.
Phương pháp
Sử dụng lý thuyết tâm đối xứng của một hình.
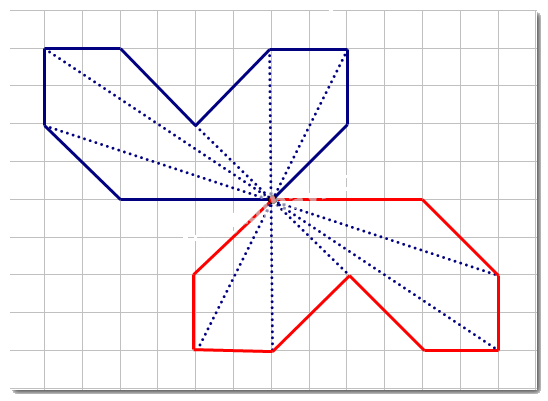
Lời giải
Hình sau khi được vẽ thêm có điểm chỉ ra trên hình vẽ là tâm đối xứng:
Trong chương trình Toán 6, việc làm quen với khái niệm đối xứng là một bước quan trọng trong việc phát triển tư duy hình học. Dạng 3: Vẽ hình có trục đối xứng, tâm đối xứng thuộc Chủ đề 9 Ôn hè Toán 6, tập trung vào việc giúp học sinh nhận biết, vẽ và xác định các yếu tố đối xứng của một hình.
Đối xứng là một tính chất quan trọng của hình học, thể hiện sự cân đối, hài hòa của hình. Có hai loại đối xứng chính:
Để vẽ một hình đối xứng qua một trục, ta cần xác định đúng trục đối xứng và vẽ các điểm đối xứng của các điểm trên hình qua trục đó. Một số hình thường gặp có trục đối xứng như:
Ví dụ: Vẽ hình vuông ABCD đối xứng qua đường thẳng d. Ta xác định các điểm A', B', C', D' đối xứng với A, B, C, D qua đường thẳng d, sau đó nối các điểm này lại để được hình vuông A'B'C'D'.
Để vẽ một hình đối xứng qua một tâm, ta cần xác định đúng tâm đối xứng và vẽ các điểm đối xứng của các điểm trên hình qua tâm đó. Một số hình thường gặp có tâm đối xứng như:
Ví dụ: Vẽ hình tròn tâm O đối xứng qua điểm I. Mọi điểm M trên đường tròn sẽ có một điểm M' đối xứng qua I, cũng nằm trên đường tròn. Tập hợp các điểm M' sẽ tạo thành hình tròn mới đối xứng với hình tròn ban đầu.
Dưới đây là một số bài tập giúp học sinh rèn luyện kỹ năng vẽ hình có trục đối xứng và tâm đối xứng:
Ngoài việc vẽ hình, học sinh cần hiểu rõ các tính chất của hình đối xứng. Ví dụ, hai tam giác đối xứng nhau thì bằng nhau. Việc nắm vững các tính chất này sẽ giúp học sinh giải quyết các bài toán phức tạp hơn.
Để học tốt dạng 3 này, học sinh cần:
Giaitoan.edu.vn hy vọng với những kiến thức và bài tập trên, các em học sinh sẽ nắm vững kiến thức về Dạng 3: Vẽ hình có trục đối xứng, tâm đối xứng - Chủ đề 9 Ôn hè Toán 6 và đạt kết quả tốt trong học tập.