Chào mừng các em học sinh đến với bài học về Dạng 2: Nhận biết hình có tâm đối xứng, thuộc Chủ đề 9 trong chương trình Ôn hè Toán 6. Bài học này sẽ giúp các em hiểu rõ khái niệm về tâm đối xứng, cách nhận biết các hình có tâm đối xứng và ứng dụng kiến thức này vào giải các bài tập thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng chi tiết, dễ hiểu cùng với hệ thống bài tập đa dạng, được thiết kế để giúp các em nắm vững kiến thức một cách nhanh chóng và hiệu quả.
Những hình có một điểm O sao cho khi quay nửa vòng quanh điểm O ta được vị trí mới của hình chồng khít với vị trí ban đầu (trước khi quay) thì được gọi là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của
Những hình có một điểm O sao cho khi quay nửa vòng quanh điểm O ta được vị trí mới của hình chồng khít với vị trí ban đầu (trước khi quay) thì được gọi là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình.
Tâm đối xứng của một số hình phẳng
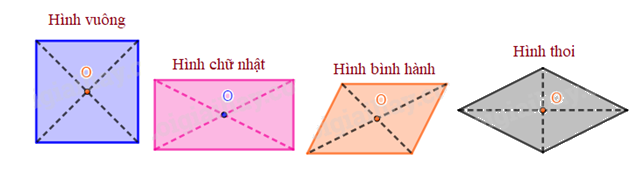
Tâm đối xứng của hình bình hành, hình thoi, hình vuông, hình chữ nhật là giao điểm của hai đường chéo.
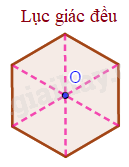
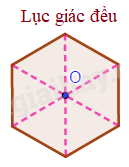
Tâm đối xứng của hình lục giác đều là giao điểm của các đường chéo chính.
Bài 1:
Chữ cái nào trong mỗi từ sau có tính đối xứng? Với mỗi từ, hãy nêu tên tỉnh thành tương ứng:
a) H O A B I N H b) N G H E A N
c) B E N T R E d) B A C K A N
e) Q U A N G T R I g) D A N A N G
Bài 2:
Trong các hình dưới đây, hình nào có tâm đối xứng?
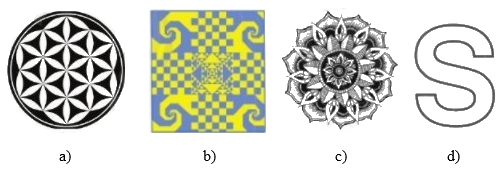
Bài 3:
Cho đoạn thẳng \(AB\) có độ dài \(4cm\). Gọi \(O\) là tâm đối xứng của đoạn thẳng \(AB\). Tính độ dài đoạn thẳng \(OA\)
Bài 4:
Hình thoi \(ABCD\) có tâm đối xứng \(O\). Biết \(OA = 3cm;\,\,OB = 2cm\). Hãy tính diện tích hình thoi.
Lời giải chi tiết:
Bài 1:
Chữ cái nào trong mỗi từ sau có tính đối xứng? Với mỗi từ, hãy nêu tên tỉnh thành tương ứng:
a) H O A B I N H b) N G H E A N
c) B E N T R E d) B A C K A N
e) Q U A N G T R I g) D A N A N G
Phương pháp
Sử dụng lý thuyết tâm đối xứng, trục đối xứng của một hình.
Lời giải
Các chữ cái H, O, I vừa có trục đối xứng, vừa có tâm đối xứn.
Chữ cái A, C, E, T, M, U có trục đối xứng.
Chữ cái N có tâm đối xứng.
Tên các tỉnh tương ứng là:
a) Hòa Bình b) Nghệ An
c) Bến Tre d) Bắc Kạn
e) Quảng Trị g) Đà Nẵng
Bài 2:
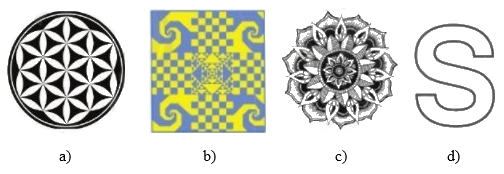
Trong các hình dưới đây, hình nào có tâm đối xứng?
Phương pháp
Sử dụng định nghĩa tâm đối xứng
Lời giải
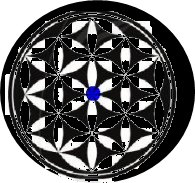
Hình a) có tâm đối xứng là điểm màu xanh có trong hình trên

Hình b) có tâm đối xứng là màu đỏ có trong hình trên

Hình c) không có tâm đối xứng vì số cánh hoa ở lớp thứ 2 (Loại cánh bị khoanh viền đỏ) là số lẻ. Nếu hình có tâm đối xứng thì đối diện của cánh hoa đó phải có 1 cánh hoa nữa nhưng điều này không xảy ra với hình trên.

Hình d) có tâm đối xứng là điểm màu đỏ.
Bài 3:
Cho đoạn thẳng \(AB\) có độ dài \(4cm\). Gọi \(O\) là tâm đối xứng của đoạn thẳng \(AB\). Tính độ dài đoạn thẳng \(OA\)
Phương pháp
Sử dụng lý thuyết tâm đối xứng.
Lời giải
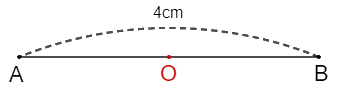
Vì \(O\) là tâm đối xứng của đoạn thẳng \(AB\) nên \(OA = OB = AB:2 = 4cm:2 = 2cm\).
Vậy \(OA = 2cm\).
Bài 4:
Hình thoi \(ABCD\) có tâm đối xứng \(O\). Biết \(OA = 3cm;\,\,OB = 2cm\). Hãy tính diện tích hình thoi.
Phương pháp
Sử dụng lý thuyết tâm đối xứng, công thức tính diện tích hình thoi.
Lời giải
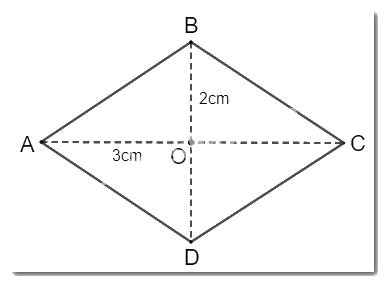
Vì \(O\) là tâm đối xứng của hình thoi \(ABCD\) nên:
\(OA = OC\) suy ra \(AC = 2OA = 2.3cm = 6cm\)
\(OB = OD\) suy ra \(BD = 2OB = 2.2cm = 4cm\)
\( \Rightarrow \) Độ dài hai đường chéo của hình thoi lần lượt là \(6cm\) và \(4cm\).
Diện tích hình thoi là: \(\frac{{6.4}}{2} = 12\,\,\left( {c{m^2}} \right)\)
Những hình có một điểm O sao cho khi quay nửa vòng quanh điểm O ta được vị trí mới của hình chồng khít với vị trí ban đầu (trước khi quay) thì được gọi là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình.
Tâm đối xứng của một số hình phẳng
Tâm đối xứng của hình bình hành, hình thoi, hình vuông, hình chữ nhật là giao điểm của hai đường chéo.
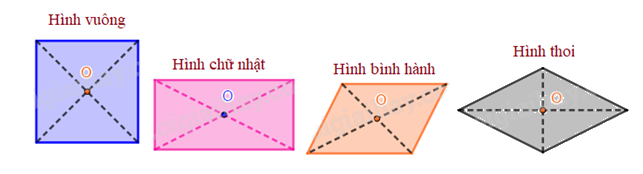
Tâm đối xứng của hình lục giác đều là giao điểm của các đường chéo chính.
Bài 1:
Chữ cái nào trong mỗi từ sau có tính đối xứng? Với mỗi từ, hãy nêu tên tỉnh thành tương ứng:
a) H O A B I N H b) N G H E A N
c) B E N T R E d) B A C K A N
e) Q U A N G T R I g) D A N A N G
Bài 2:
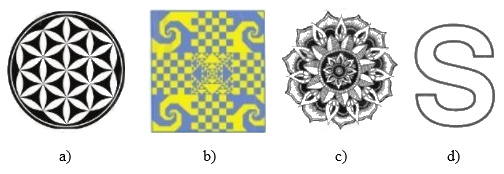
Trong các hình dưới đây, hình nào có tâm đối xứng?
Bài 3:
Cho đoạn thẳng \(AB\) có độ dài \(4cm\). Gọi \(O\) là tâm đối xứng của đoạn thẳng \(AB\). Tính độ dài đoạn thẳng \(OA\)
Bài 4:
Hình thoi \(ABCD\) có tâm đối xứng \(O\). Biết \(OA = 3cm;\,\,OB = 2cm\). Hãy tính diện tích hình thoi.
Lời giải chi tiết:
Bài 1:
Chữ cái nào trong mỗi từ sau có tính đối xứng? Với mỗi từ, hãy nêu tên tỉnh thành tương ứng:
a) H O A B I N H b) N G H E A N
c) B E N T R E d) B A C K A N
e) Q U A N G T R I g) D A N A N G
Phương pháp
Sử dụng lý thuyết tâm đối xứng, trục đối xứng của một hình.
Lời giải
Các chữ cái H, O, I vừa có trục đối xứng, vừa có tâm đối xứn.
Chữ cái A, C, E, T, M, U có trục đối xứng.
Chữ cái N có tâm đối xứng.
Tên các tỉnh tương ứng là:
a) Hòa Bình b) Nghệ An
c) Bến Tre d) Bắc Kạn
e) Quảng Trị g) Đà Nẵng
Bài 2:
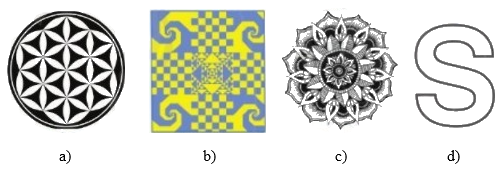
Trong các hình dưới đây, hình nào có tâm đối xứng?
Phương pháp
Sử dụng định nghĩa tâm đối xứng
Lời giải
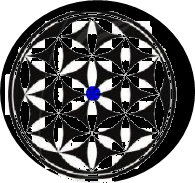
Hình a) có tâm đối xứng là điểm màu xanh có trong hình trên

Hình b) có tâm đối xứng là màu đỏ có trong hình trên

Hình c) không có tâm đối xứng vì số cánh hoa ở lớp thứ 2 (Loại cánh bị khoanh viền đỏ) là số lẻ. Nếu hình có tâm đối xứng thì đối diện của cánh hoa đó phải có 1 cánh hoa nữa nhưng điều này không xảy ra với hình trên.

Hình d) có tâm đối xứng là điểm màu đỏ.
Bài 3:
Cho đoạn thẳng \(AB\) có độ dài \(4cm\). Gọi \(O\) là tâm đối xứng của đoạn thẳng \(AB\). Tính độ dài đoạn thẳng \(OA\)
Phương pháp
Sử dụng lý thuyết tâm đối xứng.
Lời giải
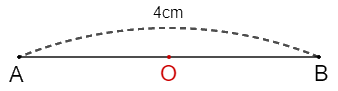
Vì \(O\) là tâm đối xứng của đoạn thẳng \(AB\) nên \(OA = OB = AB:2 = 4cm:2 = 2cm\).
Vậy \(OA = 2cm\).
Bài 4:
Hình thoi \(ABCD\) có tâm đối xứng \(O\). Biết \(OA = 3cm;\,\,OB = 2cm\). Hãy tính diện tích hình thoi.
Phương pháp
Sử dụng lý thuyết tâm đối xứng, công thức tính diện tích hình thoi.
Lời giải
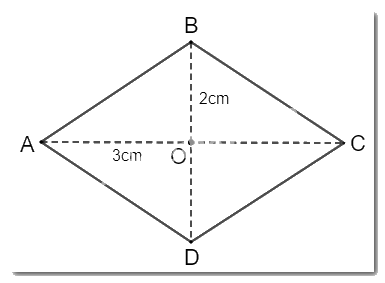
Vì \(O\) là tâm đối xứng của hình thoi \(ABCD\) nên:
\(OA = OC\) suy ra \(AC = 2OA = 2.3cm = 6cm\)
\(OB = OD\) suy ra \(BD = 2OB = 2.2cm = 4cm\)
\( \Rightarrow \) Độ dài hai đường chéo của hình thoi lần lượt là \(6cm\) và \(4cm\).
Diện tích hình thoi là: \(\frac{{6.4}}{2} = 12\,\,\left( {c{m^2}} \right)\)
Trong chương trình Toán 6, việc làm quen với các khái niệm hình học cơ bản là vô cùng quan trọng. Một trong những khái niệm đó là tâm đối xứng. Hiểu rõ về tâm đối xứng không chỉ giúp các em giải quyết các bài toán hình học một cách dễ dàng mà còn phát triển tư duy logic và khả năng quan sát.
Một hình được gọi là có tâm đối xứng nếu có một điểm, gọi là tâm đối xứng, sao cho mọi điểm của hình đều có một điểm đối xứng qua tâm đó nằm trên hình. Nói cách khác, nếu ta quay một hình 180 độ quanh tâm đối xứng của nó, hình đó sẽ trùng với chính nó.
Để nhận biết một hình có tâm đối xứng, ta có thể thực hiện các bước sau:
Dưới đây là một số bài tập giúp các em luyện tập và củng cố kiến thức về nhận biết hình có tâm đối xứng:
Khái niệm về tâm đối xứng là một phần quan trọng của chương trình hình học lớp 6. Việc nắm vững kiến thức này sẽ giúp các em tiếp cận các khái niệm hình học phức tạp hơn trong các lớp học tiếp theo. Ngoài ra, kiến thức về tâm đối xứng còn được ứng dụng rộng rãi trong thực tế, ví dụ như trong thiết kế, kiến trúc, nghệ thuật...
Để học tốt môn Toán, đặc biệt là phần hình học, các em cần:
Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!